11.3.2:多边形的内角和 同步提高课时练习(含解析)
文档属性
| 名称 | 11.3.2:多边形的内角和 同步提高课时练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 953.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 18:40:16 | ||
图片预览


文档简介
11.3.2:多边形的内角和
1.若一个多边形的内角和为1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
2.一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
3.已知正多边形的一个外角为36°,则该正多边形的边数为( ).
A.12 B.10 C.8 D.6
4.一个多边形的内角和与外角和相等,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.如果一个四边形有三个角的外角分别是80°,85°,90°,那么它的第四个角是( )
A.105° B.95° C.85° D.75°
6.若一个多边形的内角和为720°,则该多边形为( )边形.
A.四 B.五 C.六 D.七
7.若n边形的内角和等于外角和的2倍,则边数n为( )
A.n=4 B.n=5 C.n=6 D.n=7
8.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
9.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA的度数是( )
A.28° B.30° C.38° D.36°
10.如果一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是 ( )
A.5 B.6 C.7 D.8
11.设四边形的内角和等于false,五边形的外角和等于false,则false与false的关系是( )
A.false B.false C.false D.false
12.如图11-3-1,在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=false∠ADC D.∠ADE=false∠ADC
13.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x,y,z,则false的值为( )
A.1 B.false C.false D.false
14.如图,足球图片正中的黑色正五边形的内角和是( ).
A.180° B.360° C.540° D.720°
15.如图,小明从false点出发,沿直线前进10米后向左转10°再沿直线前进10米后向左转20°再沿直线前进10米后向左转30°……照这样下去,他第一次回到出发地false点时,一共走了( )
A.80米 B.160米
C.300米 D.640米
16.在多边形内角和公式的探究过程中,主要运用的数学思想是( )
A.化归思想 B.分类讨论 C.方程思想 D.数形结合思想
17.小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2016°,则n等于( )
A.11 B.12 C.13 D.14
18.能够铺满地面的正多边形组合是( )
A.正三角形和正五边形 B.正方形和正六边形
C.正方形和正五边形 D.正五边形和正十边形
19.如图,该硬币边缘镌刻的正九边形每个内角的度数是_____.
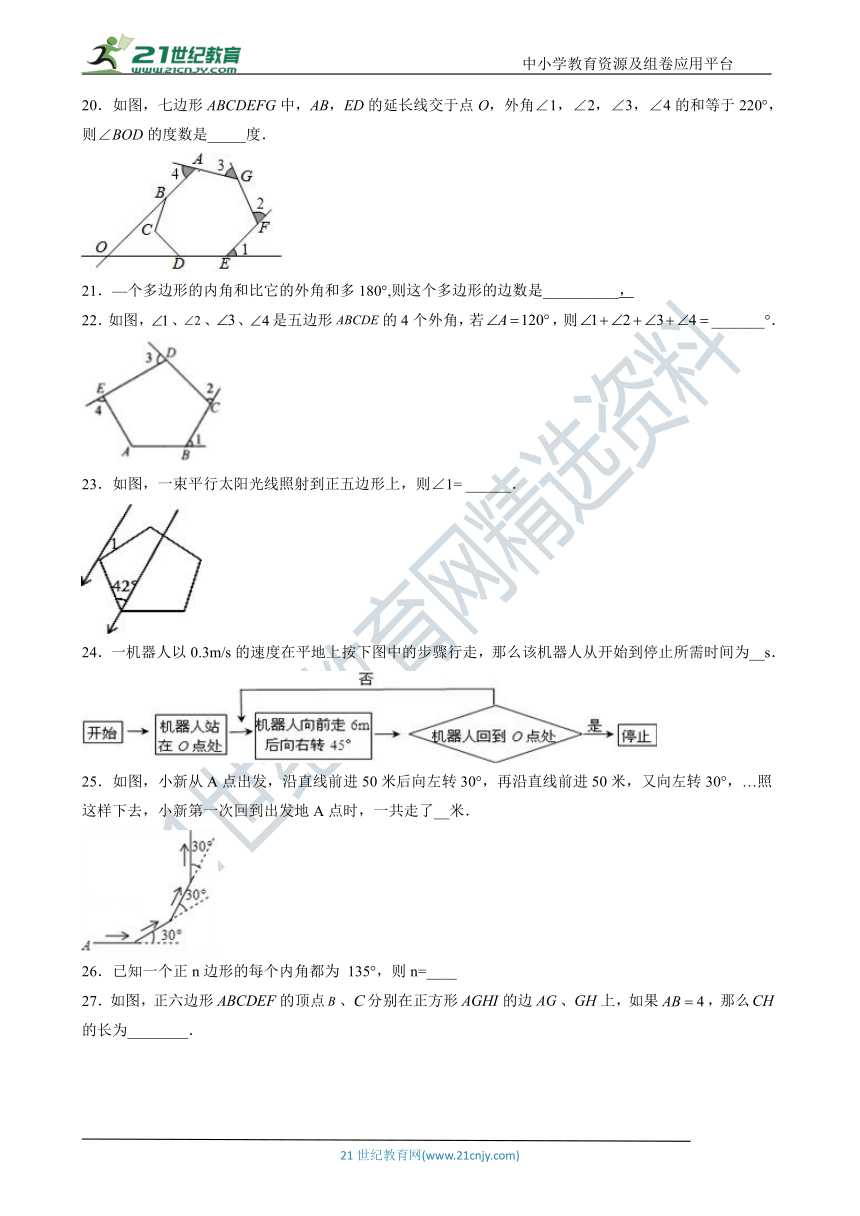
20.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,外角∠1,∠2,∠3,∠4的和等于220°,则∠BOD的度数是_____度.
21.—个多边形的内角和比它的外角和多180°,则这个多边形的边数是__________,
22.如图,false、false、false、false是五边形false的4个外角,若false,则false_______°.
23.如图,一束平行太阳光线照射到正五边形上,则∠1= ______.
24.一机器人以0.3m/s的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为__s.
25.如图,小新从A点出发,沿直线前进50米后向左转30°,再沿直线前进50米,又向左转30°,…照这样下去,小新第一次回到出发地A点时,一共走了__米.
26.已知一个正n边形的每个内角都为 135°,则n=____
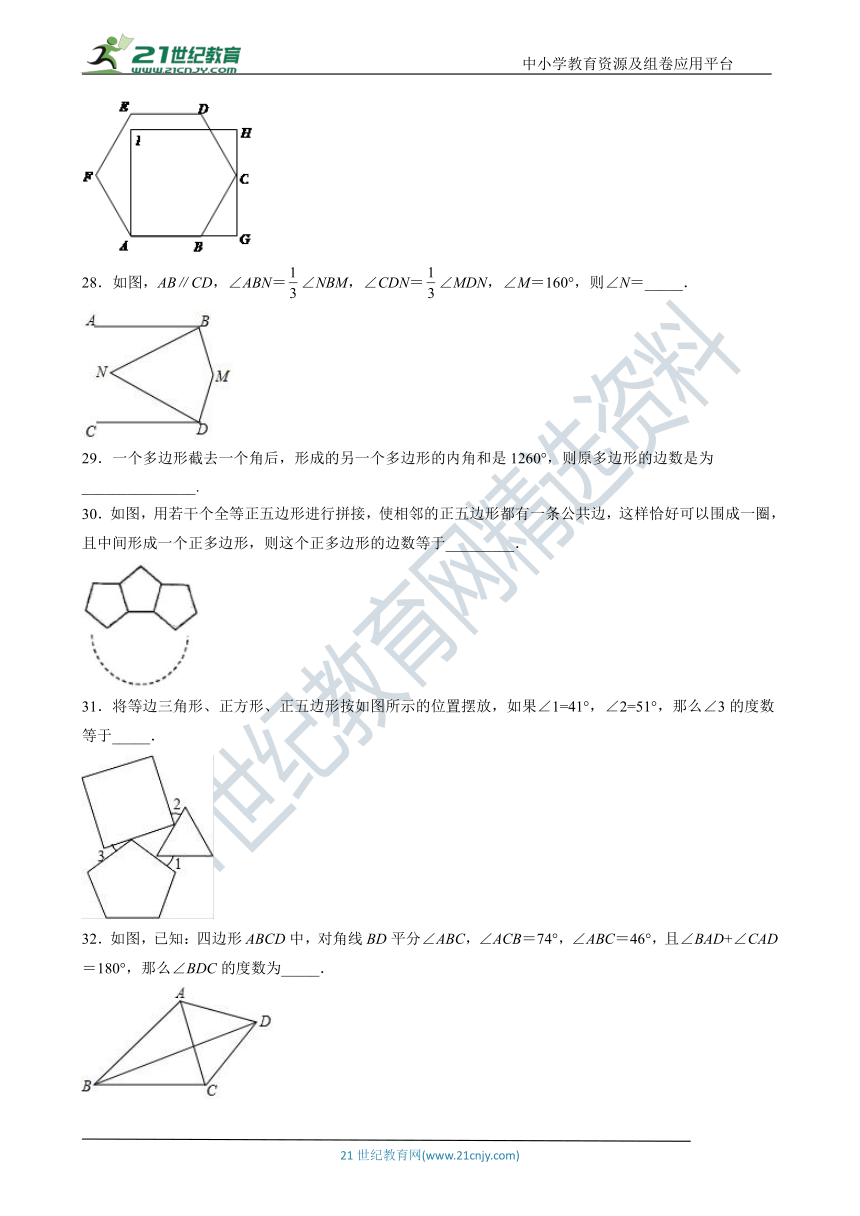
27.如图,正六边形false的顶点false、false分别在正方形false的边false、false上,如果false,那么false的长为________.
28.如图,AB∥CD,∠ABN=false∠NBM,∠CDN=false∠MDN,∠M=160°,则∠N=_____.
29.一个多边形截去一个角后,形成的另一个多边形的内角和是1260°,则原多边形的边数是为_______________.
30.如图,用若干个全等正五边形进行拼接,使相邻的正五边形都有一条公共边,这样恰好可以围成一圈,且中间形成一个正多边形,则这个正多边形的边数等于_________.
31.将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=41°,∠2=51°,那么∠3的度数等于_____.
32.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=74°,∠ABC=46°,且∠BAD+∠CAD=180°,那么∠BDC的度数为_____.
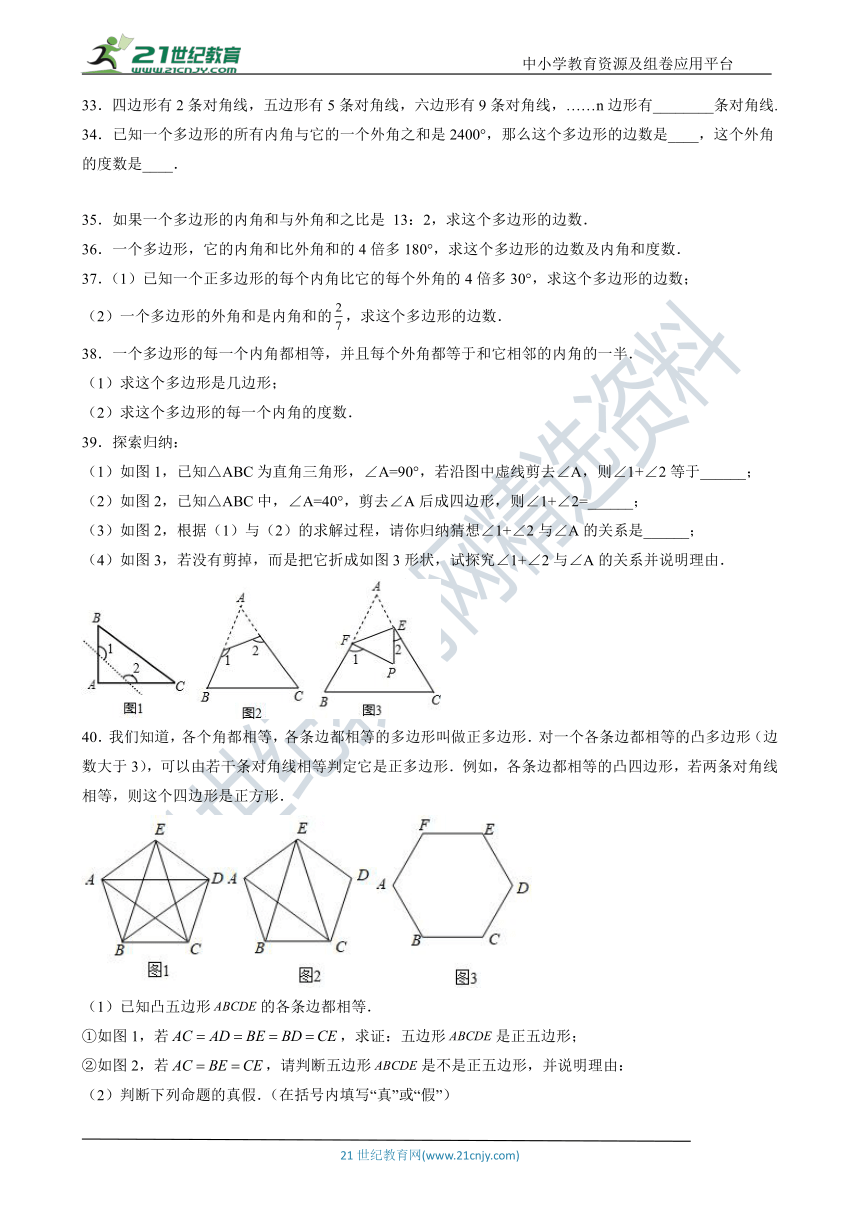
33.四边形有2条对角线,五边形有5条对角线,六边形有9条对角线,……n边形有________条对角线.
34.已知一个多边形的所有内角与它的一个外角之和是2400°,那么这个多边形的边数是____,这个外角的度数是____.
35.如果一个多边形的内角和与外角和之比是 13:2,求这个多边形的边数.
36.一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
37.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;
(2)一个多边形的外角和是内角和的false,求这个多边形的边数.
38.一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
39.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于______;
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=______;
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是______;
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
40.我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
(1)已知凸五边形false的各条边都相等.
①如图1,若false,求证:五边形false是正五边形;
②如图2,若false,请判断五边形false是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形false的各条边都相等.
①若false,则六边形false是正六边形;( )
②若false,则六边形false是正六边形. ( )
41.如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
42.(1)已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.
(2)一个正多边形的内角和为1800°,求这个多边形的边数.
43.请按照研究问题的步骤依次完成任务.
(问题背景)
(1)如图1的图形我们把它称为“8字形”, 请说理证明∠A+∠B=∠C+∠D.
(简单应用)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)
(问题探究)
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE, 若∠ABC=36°,∠ADC=16°,猜想∠P的度数为 ;
(拓展延伸)
(4)在图4中,若设∠C=x,∠B=y,∠CAP=false∠CAB,∠CDP=false∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P) ;
(5)在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、D的关系,直接写出结论 .
44.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
45.false中,false,点false分别是边false上的点,点false是一动点,令false,false,false.
(1)若点false在线段false上,如图①所示,且false,则false_____false;
(2)若点false在边false上运动,如图②所示,则false、false、false之间的关系为______;
(3)如图③,若点false在斜边false的延长线上运动false,请写出false、false、false之间的关系式,并说明理由.
参考答案
1.C
【解答】多边形内角和定理.
【分析】设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),即可得方程180(n﹣2)=1080,
解此方程即可求得答案:n=8.故选C.
2.C
【解析】一个外角的度数是:180°-140°=40°,
则多边形的边数为:360°÷40°=9;
故选C.
【解答】
3.B
【解析】利用多边形的外角和是360°,正多边形的每个外角都是36°,即可求出答案.
【解答】解:360°÷36°=10,所以这个正多边形是正十边形.
故选B.
【点评】本题主要考查了多边形的外角和定理.是需要识记的内容.
4.A
【解答】多边形的内角和外角性质.
【分析】设此多边形是n边形,
∵多边形的外角和为360°,内角和为(n-2)180°,
∴(n-2)180=360,解得:n=4.
∴这个多边形是四边形.故选A.
5.D
【解析】四边形的外角和为360°,已知三个角的外角和,求出第四个角的外角度数,则得到第四个角的度数.
【解答】四边形第四个角的外角度数:360°-80°-85°-90°=105°
则第四个角是
180°-105°=75°
故答案选D.
【点评】本题考查多边形的内角和与外角和综合,理解多边形的外角和等于360°和多边形的外角与它相邻的内角互补是解题关键.
6.C
【解析】设多边形为n边形,由多边形的内角和定理列出方程求解即可.
【解答】解:设多边形为n边形.
由题意得:(n-2) ·180°=720°,
解得:n=6.
故选C.
【点评】本题考查多边形的内角和定理,n边形的内角和为:(n-2) ·180°.
7.C
【解答】由题意得(n-2)×180=360×2,解得n=6,
故选C.
8.D
【解答】试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)?180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
考点:多边形内角与外角.
9.D
【解析】根据两直线平行,内错角相等,得到∠DFA=∠CDB,根据三角形的内角和求出∠CDB的度数从而得到∠DFA的度数.
【解答】解:∠C=false,且CD=CB,
∴∠CDB=∠CBD
∵由三角形的内角和∠C+∠CDB+∠CBD=180°
∴∠CDB+∠CBD=180°-∠C =180°-108°=72°
∴∠CDB==∠CBD=false
又∵AF∥CD
∴∠DFA=∠CDB=36°(两直线平行,内错角相等)
故选D
【点评】本题主要考查多边形的基本概念和三角形的基本概念,正n边形的内角读数为false.
10.C
【解答】
设多边形原有边数为x,
则(2x?2)×180=2160,
2x?2=12,解得x=7,
故本题选C.
11.B
【解析】根据多边形的内角和定理与多边形外角的关系即可得出结论.
【解答】解:∵四边形的内角和等于a,
∴a=(4-2)?180°=360°.
∵五边形的外角和等于false,
∴false =360°,
∴a=false.
故选B.
【点评】本题考查的是多边形的内角与外角,熟知多边形的内角和定理是解答此题的关键.
12.D
【解答】设∠ADE=x,∠ADC=y,由题意可得,
∠ADE+∠AED+∠A=180°,∠A+∠B+∠C+∠ADC=360°,
即x+60+∠A=180①,3∠A+y=360②,
由①×3-②可得3x-y=0,
所以false,即∠ADE=false∠ADC.
故答案选D.
考点:三角形的内角和定理;四边形内角和定理.
13.C
【解析】
分析:根据边数求出各个多边形的每个内角的度数,结合镶嵌的条件列出方程,进而即可求出答案.
详解:由题意知,这3种多边形的3个内角之和为360度,已知正多边形的边数为x、y、z,那么这三个多边形的内角和可表示为:false+false+false=360,两边都除以180得:1﹣false+1﹣false+1﹣false=2,两边都除以2得:false+false+false=false.
故选C.
点睛:解决本题的关键是知道这3种多边形的3个内角之和为360度,据此进行整理分析得解.
14.C
【解析】根据多边形内角和公式false即可求出结果.
【解答】解:黑色正五边形的内角和为:false,
故选C.
【点评】本题考查了多边形的内角和公式,解题关键是牢记多边形的内角和公式.
15.A
【解析】利用多边形的外角和得出小明回到出发地false点时左转的次数,即可求出多边形的边数,即可解决问题.
【解答】解:由题意可知,小明第一次回到出发地false点时,他一共转了false,由题意得10°+20° +30°+40°+50°+60°+70°+80°=360°,所以共转了8次,每次沿直线前进10米,所以一共走了80米.
故选:A.
【点评】本题考查根据多边形的外角和解决实际问题,注意多边形的外角和是false,要注意第一次转了10°,第二次转了20°,第三次转了30°……,利用好规律解题.
16.A
【解析】根据多边形内角和定理:(n-2)·180(n≥3)且n为整数)的推导过程即可解答.
【解答】解:多边形内角和定理:(n-2)·180(n≥3)且n为整数),该公式推导的基本方法是从n边形的一个顶点出发引出(n-3)条对角线,将n边形分割为(n-2)个三角形,这(n-2)个三角形的所有内角之和正好是n边形的内角和,体现了化归思想.
故答案为A.
【点评】本题主要考查了在数学的学习过程应用的数学思想,弄清推导过程是解答此题的关键.
17.C
【解答】解:根据多边形的内角和公式(n-2)×180°,可以求得n=13.2,由于多加的是内角,
所以多加的角为小于180°的角,所以去掉小数部分就是n边形的边数.故选C
18.D
【解析】
【解析】正多边形的组合能否铺满地面,关键是要看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
【解答】解:A、正五边形和正三边形内角分别为108°、60°,由于60m+108n=360,得m=6-falsen,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;
B、正方形、正六边形内角分别为90°、120°,不能构成360°的周角,故不能铺满,故此选项错误;
C、正方形、正五边形内角分别为90°、108°,当90n+108m=360,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;
D、正五边形和正十边形内角分别为108、144,两个正五边形与一个正十边形能铺满地面,故此选项正确.
故选:D.
【点评】此题主要考查了平面镶嵌,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°-360°÷边数.
19.140°.
【解析】先根据多边形内角和定理:false求出该多边形的内角和,再求出每一个内角的度数.
【解答】解:该正九边形内角和false,
则每个内角的度数false.
故答案为140°.
【点评】本题主要考查了多边形的内角和定理:false,比较简单,解答本题的关键是直接根据内角和公式计算可得内角和.
20.40.
【解析】在DO延长线上找一点M,根据多边形的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【解答】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∴∠BOM=360°﹣220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°﹣∠BOM=180°﹣140°=40°.
故答案为:40
【点评】本题考查多边形的角度计算,关键在于熟记外角和360°.
21.5
【解析】设这个多边形的边数是n,则内角和为(n-2)×180°,故可列出方程求解.
【解答】设这个多边形的边数是n,则内角和为(n-2)×180°,
依题意得(n-2)×180°-360°=180°
解得n=5
故填:5.
【点评】此题主要考查多边形的内角和与外角和,解题的关键是熟知多边形的内角和与外角和公式.
22.false
【解答】解:由题意得,∠A的外角=180°-∠A=60°,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°-∠A的外角=300°.
故答案为:300.
【点评】本题考查多边形外角性质,补角定义.
23.30°.
【解答】解:∵AB//CD,∴∠BAC+∠ACD=180°,即∠1+∠EAC+∠ACD=180°,
∵五边形是正五边形,∴∠EAC=108°,
∵∠ACD=42°,∴∠1=180°-42°-108°=30°
故答案为:30°.
24.160.
【解析】
试题分析:该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数,即可求得周长,利用周长除以速度即可求得所需时间.
试题解析:360÷45=8,
则所走的路程是:6×8=48m,
则所用时间是:48÷0.3=160s.
考点:多边形内角与外角.
25.600
【解答】解:根据题意可知:小新从A点出发,沿直线前进50米后向左转30?,再沿直线前进50米,又向左转30?,……照这样下去,小新第一次回到出发地A点时,小新走的路线围成一个正多边形,且这个多边形的外角等于30?,所以这个正多边形的边数是12,小新一共走了12×50=600米,
故答案为:600.
26.8
【解析】
【解析】由一个正多边形的每个内角都为135°,可求得其外角的度数,继而可求得此多边形的边数,则可求得答案.
【解答】∵一个正n边形的每个内角都为135°,
∴这个正n边形的每个外角都为:180°-135°=45°,
∴这个n边形的边数为:360°÷45°=8,
故答案为:8.
【点评】此题考查了多边形的内角和与外角和的知识.此题难度不大,注意掌握多边形的内角和与外角和定理是关键.
27.false
【解析】
分析:求出正六边形的内角的度数,根据直角三角形的性质求出BG、CG,根据正多边形的性质计算.
详解:∵正六边形的每个内角=false,
则∠CBG=180°-120°=60°,
∴∠BCG=30°,
∴BG=falseBC=2,CG=falseBC=false,
∴AG=AB+BG=6,
∵四边形AGHI是正方形,
∴GH=AG=6,
∴CH=HG-CG=false,
故答案为false.
点睛:本题考查的是正多边形的有关计算,掌握正多边形的性质、内角的计算公式是解题的关键.
28.50°
【解析】过M作ME∥AB,AB∥ME∥CD,即可得到∠ABM+∠BMD+∠CDM=180°×2=360°,再根据false,
可得false,即可得到四边形BMDN中,∠N=360°﹣150°﹣160°=50°.
【解答】如图所示,过M作ME∥AB,则
∵AB∥CD,
∴AB∥ME∥CD,
∴∠ABM+∠BMD+∠CDM=180°×2=360°,
又∵∠BMD=160°,
∴∠ABM+∠CDM=200°,
又∵false,
∴false,
∴四边形BMDN中,∠N=360°﹣150°﹣160°=50°,
故答案为:50°.
【点评】本题主要考查了平行线的性质和四边形的内角和,解题的关键在于掌握两直线平行,同旁内角互补的性质.
29.8或9或10
【解析】先根据多边形的内角和公式(n﹣2)?180°求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
【解答】设多边形截去一个角的边数为n,根据题意得:
(n﹣2)?180°=1260°
解得:n=9.
∵截去一个角后边上可以增加1,不变,减少1,∴原多边形的边数是8或9或10.
故答案为8或9或10.
【点评】本题考查了多边形的内角和公式,本题难点在于多边形截去一个角后边数有增加1,不变,减少1三种情况.
30.10
【解析】首先求得正五边形围成的多边形的内角的度数,然后根据多边形的内角和定理即可求得答案.
【解答】解:正五边形的内角度数是:false=108°,
则正五边形围成的多边形的内角的度数是:360°?2×108°=144°,
根据题意得:180(n?2)=144n,
解得:n=10.
故答案为10.
【点评】本题考查了多边形的内角和定理,正确理解定理,求得围成的多边形的内角的度数是关键.
31.10°
【解答】试题分析:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:false(5﹣2)×180°=108°,则∠3=360°﹣60°﹣90°﹣108°﹣∠1﹣∠2=10°.故答案为10°.
考点:1.多边形内角与外角;2.三角形内角和定理.
32.30°
【解析】延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,根据BD是∠ABC的平分线可得出△BDE≌△BDF,故DE=DF,过D点作DG⊥AC于G点,可得出△ADE≌△ADG,△CDG≌△CDF,进而得出CD为∠ACF的平分线,得出∠DCA=53°,再根据三角形内角和定理即可得出结论.
【解答】解:
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,
∵BD是∠ABC的平分线
在△BDE与△BDF中,false ,
∴△BDE≌△BDF(ASA),
∴DE=DF,
又∵∠BAD+∠CAD=180°
∠BAD+∠EAD=180°
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
过D点作DG⊥AC于G点,
在Rt△ADE与Rt△ADG中,false ,
∴△ADE≌△ADG(HL),
∴DE=DG,
∴DG=DF.
在Rt△CDG与Rt△CDF中,false ,
∴Rt△CDG≌Rt△CDF(HL),
∴CD为∠ACF的平分线,
∠ACB=74°,
∴∠DCA=53°,
∴∠BDC=180°﹣∠CBD﹣∠DCA﹣∠ACB=180°﹣23°﹣53°﹣74°=30°.
故答案为:30°
【点评】本题考查了多边形的外角和内角,能熟记三角形的外角性质和三角形的内角和定理是解此题的关键,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和.
33.false
【解答】四边形有2条(false )对角线,五边形有5条(false)对角线,六边形有9条(false)对角线,故n边形有false条对角线.
故答案:false.
34.15 60°
【解析】设这个多边形边数是n,表示出一个外角的范围,求出不等式的解集确定出正整数n的值,即为多边形的边数,继而求出这个外角即可.
【解答】解:设这个多边形的边数是n,n为正整数,
根据题意得:0<2400°-(n-2)×180°<180°,
解得:14.3这个外角为2400°-(15-2)×180°=60°,
故答案为:15;60°
【点评】本题考查了多边形内角与外角,熟练掌握内角和定理是解答此题的关键.
35.15.
【解析】设这个多边形的边数为false,依据多边形的内角和与外角和之比是false,即可得到false的值.
【解答】解:设这个多边形的边数为false,依题意得:
false,
解得false,
false这个多边形的边数为15.
【点评】考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,多边形的外角和等于360度.
36.这个多边形的边数是11,内角和度数是1620度.
【解答】试题分析:又多边形的外角和是360°,得到内角和是1620度.n边形的内角和可以表示成(n﹣2)?180°,设这个多边形的边数是n,就得到方程,从而求出边数.
试题解析:根据题意,得:(n﹣2)?180=1620,解得:n=11.则这个多边形的边数是11,内角和度数是1620度.
考点:多边形内角与外角.
37.(1) 这个多边形的边数是12边形;(2)这个多边形的边数为9.
【解析】(1)一个正多边形的每个内角比它相邻的外角的4倍还多30°,又由于内角与外角的和是180度.设内角是x°,外角是y°,列方程组求解;
(2)设这个多边形的边数为n,由n边形的内角和是(n-2)?180°,多边形的外角和是360°列出方程,解方程求出n的值即可.
【解答】(1)设内角是x°,外角是y°,
则得到一个方程组false
解得false.
而任何多边形的外角是360°,
则多边形内角和中的外角的个数是360÷30=12,
则这个多边形的边数是12边形;
(2)设这个多边形的边数为n,
依题意得:false(n-2)180°=360°,
解得n=9,
答:这个多边形的边数为9.
【点评】此题考查多边形内角与外角,正确的列出方程组是解题的关键.
38.(1)这个多边形是六边形;(2)这个多边形的每一个内角的度数是120°.
【解析】(1)先设内角为x,根据题意可得:外角为false,根据相邻内角和外角的关系可得:,x+false =180°,从而解得:x=120°,即外角等于60°,根据外角和等于360°可得这个多边形的边数为:false=6,
(2)先设内角为x,根据题意可得:外角为false,根据相邻内角和外角的关系可得:,x+false =180°,从而解得内角:x=120°,内角和=(6﹣2)×180°=720°.
【解答】(1)设内角为x,则外角为false,
由题意得,x+false =180°,
解得:x=120°,
false=60°,
这个多边形的边数为:false=6,
答:这个多边形是六边形,
(2)设内角为x,则外角为false,
由题意得: x+false =180°,
解得:x=120°,
答:这个多边形的每一个内角的度数是120度.
内角和=(6﹣2)×180°=720°.
【点评】本题主要考查多边形内角和外角,多边形内角和以及多边形的外角和,解决本题的关键是要熟练掌握多边形内角和外角的关系以及多边形内角和.
39.(1)270°;(2)220°;(3)∠1+∠2=180°+∠A ;(4)∠1+∠2=2∠A,理由见解析
【解析】(1)先求出∠B+∠C的度数,再根据四边形内角和等于360°,即可求解;
(2)先求出∠B+∠C的度数,再根据四边形内角和等于360°,即可求解;
(3)先用∠A表示出∠B+∠C,再根据四边形内角和等于360°,即可得到结论;
(4)由折叠的性质得∠AFE=∠PFE,∠AEF=∠PEF,结合平角的定义和三角形内角和定理,即可得到结论.
【解答】(1)∵△ABC为直角三角形,∠A=90°,
∴∠B+∠C=180°-90°=90°,
∴∠1+∠2=360°-(∠B+∠C)=270°.
故答案是:270°;
(2)∵△ABC中,∠A=40°,
∴∠B+∠C=180°-40°=140°,
∴∠1+∠2=360°-(∠B+∠C)=220°.
故答案是:220°;
(3)猜想:∠1+∠2=180°+∠A,理由如下:
∵△ABC中,∠B+∠C=180°-∠A,
∴∠1+∠2=360°-(∠B+∠C)=360°-(180°-∠A)=180°+∠A.
故答案是:∠1+∠2=180°+∠A;
(4)?∠1+∠2=2∠A,理由如下:
∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,
∴∠1+∠2=360°-2(∠AFE+∠AEF),
又∵∠AFE+∠AEF=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A.
【点评】本题主要考查三角形内角和定理,四边形内角和等于360°以及折叠的性质,熟练掌握三角形内角和定理,四边形内角和等于360°,是解题的关键.
40.(1)①证明见解析②若false,五边形false是正五边形(2)①真命题②真命题
【解析】(1)①用SSS证明false,得到false,即可得证;
②先证false,再证明false,再根据四边形的内角和与平行的性质证得false即可得证;
(2)①先证false,再举出等腰直角三角形的反例,得出false,由此即可得出结论;
②连接false、false、false,先证false,再证false,得到false,再由(2)①即可得出结论.
【解答】(1)①证明:∵凸五边形false的各条边都相等
∴false
在false、false、false、false、false中,false
∴false
∴false
∴五边形false是正五边形;
②解:若false,五边形false是正五边形,理由如下:
在false、false和false中,false
∴false
∴false,false
在false和false中,false
∴false
∴false,false
∵四边形false内角和为false
∴false
∴false
∴false,false
∴false
∴false
同理:false
∴五边形false是正五边形;
(2)解:①若false,则六边形false是正六边形;假命题,理由如下:
如图3所示,∵凸六边形false的各条边都相等
∴false
在false、false和false中,false
∴false
因此,如果false都为相同的等腰直角三角形,符合题意
但false,而正六边形的每个内角都为false
∴六边形false不是正六边形
故答案为:假;
②若false,则六边形false是正六边形;假命题;理由如下:
如图4所示:连接false、false、false
在false和false中,false
∴false
∴false
∵false
∴false
∴false
在false和false中,false
∴false
∴false
同理:false
∴false
由(2)①可知:六边形false不是正六边形
故答案为:假.
【点评】本题主要考查正多边形的证明,解题的关键是熟知全等三角形的判定与性质.
41.∠MON=33°.
【解析】由正方形、正五边形和正六边形的性质得到∠AOM=108°,∠OBC=120°,∠NBC=90°,求得∠AOB=false×120°=60°,∠MOB=108°-60°=48°,得到∠OBN=360°-120°-90°=150°,根据角和差即可得到结论.
【解答】解:如图,
由正方形、正五边形和正六边形的定义得:
∠AOM=108°,∠OBC= 120°,∠NBC =90°,
∴∠AOB=false120°=60°,∠MOB = 108° – 60°= 48°,
∴∠OBN= 360°- 120°- 90°= 150°,
∴∠NOB=false(180°-150°)=15°,
∴∠MON=48°-15°=33°.
【点评】本题考查了多边形的内角和外角,熟练掌握正方形、正五边形和正六边形的内角的度数是解题的关键.
42.(1)150°、120°、90°.(2)12.
【解析】(1)解答本题需要熟练掌握三角形内角和定理的知识,熟知三角形的内角和等于180°.通过解题,求出三个内角,再根据内角加对应的外交和等于180°算出外角;
(2)根据多边形内角和即可求出.
【解答】(1)设此三角形三个内角的比为x,2x,3x,
则x+2x+3x=180,
6x=180,
x=30,
则三个内角分别为30°、60°、90°,
相应的三个外角分别为150°、120°、90°.
(2)设这个多边形的边数是n,
则(n﹣2)?180°=1800°,
解得n=12.
故这个多边形的边数为12.
【点评】本题考查的知识点是多边形内角和,解题的关键是熟练的掌握多边形内角和.
43.(1)见解析;(2)∠P=23?;(3)∠P=26?;(4)∠P=false;(5)∠P=false.
【解析】(1)根据三角形内角和定理即可证明;
(2)如图2,根据角平分线的性质得到∠1=∠2,∠3=∠4,列方程组即可得到结论;
(3)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°-∠2,∠PCD=180°-∠3,由∠P+(180°-∠1)=∠D+(180°-∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解决问题;
(4)根据题意得出∠B+∠CAB=∠C+∠BDC,再结合∠CAP=false∠CAB,∠CDP=false∠CDB,得到y+(∠CAB-false∠CAB)=∠P+(∠BDC-false∠CDB),从而可得∠P=y+∠CAB-false∠CAB-∠CDB+false∠CDB=false;
(5)根据题意得出∠B+∠BAD=∠D+∠BCD,∠DAP+∠P=∠PCD+∠D,再结合AP平分∠BAD,CP平分∠BCD的外角∠BCE,得到false∠BAD+∠P=[∠BCD+false(180°-∠BCD)]+∠D,所以∠P=90°+false∠BCD-false∠BAD +∠D=false.
【解答】解:(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)解:如图2,∵AP、CP分别平分∠BAD,∠BCD,
∴∠1=∠2,∠3=∠4,
由(1)的结论得:false,
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D,
∴∠P=false(∠B+∠D)=23°;
(3)解:如图3,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°-∠2,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠D+(180°-∠3),
∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=false(∠B+∠D)=false×(36°+16°)=26°;
故答案为:26°;
(4)由题意可得:∠B+∠CAB=∠C+∠BDC,
即y+∠CAB=x+∠BDC,即∠CAB-∠BDC=x-y,
∠B+∠BAP=∠P+∠PDB,
即y+∠BAP=∠P+∠PDB,
即y+(∠CAB-∠CAP)=∠P+(∠BDC-∠CDP),
即y+(∠CAB-false∠CAB)=∠P+(∠BDC-false∠CDB),
∴∠P=y+∠CAB-false∠CAB-∠CDB+false∠CDB
= y+false(∠CAB-∠CDB)
=y+false(x-y)
=false
故答案为:∠P=false;
(5)由题意可得:∠B+∠BAD=∠D+∠BCD,
∠DAP+∠P=∠PCD+∠D,
∴∠B-∠D=∠BCD-∠BAD,
∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠BAP=∠DAP,∠PCE=∠PCB,
∴false∠BAD+∠P=(∠BCD+false∠BCE)+∠D,
∴false∠BAD+∠P=[∠BCD+false(180°-∠BCD)]+∠D,
∴∠P=90°+false∠BCD-false∠BAD +∠D
=90°+false(∠BCD-∠BAD)+∠D
=90°+false(∠B-∠D)+∠D
=false,
故答案为:∠P=false.
【点评】本题考查三角形内角和,三角形的外角的性质、多边形的内角和等知识,解题的关键是学会用方程组的思想思考问题,属于中考常考题型.
44.∠COD=100°
【解析】由于∠A+∠B=200°,根据四边形的内角和定理求出∠ADC+∠DCB的度数,然后根据角平分线的定义得出∠ODC+∠OCD的度数,最后根据三角形内角和定理求出∠COD的度数.
【解答】解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°﹣200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=false∠ADC,∠OCD=false∠BCD,
∴∠ODC+∠OCD=false×160°=80°,
∴∠COD=180°﹣80°=100°.
【点评】本题主要考查了三角形及四边形的内角和定理.三角形的内角和等于180°;四边形的内角和等于360°.
45.(1)140°;(2)∠1+∠2=90°+α.(3)如图1,∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠1?∠2=∠α?90°.
【解析】(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质分三种情况讨论即可.
【解答】(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°;
(2)由(1)得出:∠α+∠C=∠1+∠2,∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点,如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,∴∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠2=∠1?∠α+∠C,∴∠1?∠2=∠α?90°.
【点评】本题考查三角形内角和定理和外角的性质、对顶角相等的性质和四边形内角和定理,熟练利用三角形外角的性质是解决问题的关键.
1.若一个多边形的内角和为1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
2.一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
3.已知正多边形的一个外角为36°,则该正多边形的边数为( ).
A.12 B.10 C.8 D.6
4.一个多边形的内角和与外角和相等,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.如果一个四边形有三个角的外角分别是80°,85°,90°,那么它的第四个角是( )
A.105° B.95° C.85° D.75°
6.若一个多边形的内角和为720°,则该多边形为( )边形.
A.四 B.五 C.六 D.七
7.若n边形的内角和等于外角和的2倍,则边数n为( )
A.n=4 B.n=5 C.n=6 D.n=7
8.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
9.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA的度数是( )
A.28° B.30° C.38° D.36°
10.如果一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是 ( )
A.5 B.6 C.7 D.8
11.设四边形的内角和等于false,五边形的外角和等于false,则false与false的关系是( )
A.false B.false C.false D.false
12.如图11-3-1,在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=false∠ADC D.∠ADE=false∠ADC
13.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x,y,z,则false的值为( )
A.1 B.false C.false D.false
14.如图,足球图片正中的黑色正五边形的内角和是( ).
A.180° B.360° C.540° D.720°
15.如图,小明从false点出发,沿直线前进10米后向左转10°再沿直线前进10米后向左转20°再沿直线前进10米后向左转30°……照这样下去,他第一次回到出发地false点时,一共走了( )
A.80米 B.160米
C.300米 D.640米
16.在多边形内角和公式的探究过程中,主要运用的数学思想是( )
A.化归思想 B.分类讨论 C.方程思想 D.数形结合思想
17.小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2016°,则n等于( )
A.11 B.12 C.13 D.14
18.能够铺满地面的正多边形组合是( )
A.正三角形和正五边形 B.正方形和正六边形
C.正方形和正五边形 D.正五边形和正十边形
19.如图,该硬币边缘镌刻的正九边形每个内角的度数是_____.
20.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,外角∠1,∠2,∠3,∠4的和等于220°,则∠BOD的度数是_____度.
21.—个多边形的内角和比它的外角和多180°,则这个多边形的边数是__________,
22.如图,false、false、false、false是五边形false的4个外角,若false,则false_______°.
23.如图,一束平行太阳光线照射到正五边形上,则∠1= ______.
24.一机器人以0.3m/s的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为__s.
25.如图,小新从A点出发,沿直线前进50米后向左转30°,再沿直线前进50米,又向左转30°,…照这样下去,小新第一次回到出发地A点时,一共走了__米.
26.已知一个正n边形的每个内角都为 135°,则n=____
27.如图,正六边形false的顶点false、false分别在正方形false的边false、false上,如果false,那么false的长为________.
28.如图,AB∥CD,∠ABN=false∠NBM,∠CDN=false∠MDN,∠M=160°,则∠N=_____.
29.一个多边形截去一个角后,形成的另一个多边形的内角和是1260°,则原多边形的边数是为_______________.
30.如图,用若干个全等正五边形进行拼接,使相邻的正五边形都有一条公共边,这样恰好可以围成一圈,且中间形成一个正多边形,则这个正多边形的边数等于_________.
31.将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=41°,∠2=51°,那么∠3的度数等于_____.
32.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=74°,∠ABC=46°,且∠BAD+∠CAD=180°,那么∠BDC的度数为_____.
33.四边形有2条对角线,五边形有5条对角线,六边形有9条对角线,……n边形有________条对角线.
34.已知一个多边形的所有内角与它的一个外角之和是2400°,那么这个多边形的边数是____,这个外角的度数是____.
35.如果一个多边形的内角和与外角和之比是 13:2,求这个多边形的边数.
36.一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
37.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;
(2)一个多边形的外角和是内角和的false,求这个多边形的边数.
38.一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
39.探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于______;
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=______;
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是______;
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.
40.我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
(1)已知凸五边形false的各条边都相等.
①如图1,若false,求证:五边形false是正五边形;
②如图2,若false,请判断五边形false是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形false的各条边都相等.
①若false,则六边形false是正六边形;( )
②若false,则六边形false是正六边形. ( )
41.如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
42.(1)已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.
(2)一个正多边形的内角和为1800°,求这个多边形的边数.
43.请按照研究问题的步骤依次完成任务.
(问题背景)
(1)如图1的图形我们把它称为“8字形”, 请说理证明∠A+∠B=∠C+∠D.
(简单应用)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)
(问题探究)
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE, 若∠ABC=36°,∠ADC=16°,猜想∠P的度数为 ;
(拓展延伸)
(4)在图4中,若设∠C=x,∠B=y,∠CAP=false∠CAB,∠CDP=false∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P) ;
(5)在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、D的关系,直接写出结论 .
44.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,求∠COD的度数.
45.false中,false,点false分别是边false上的点,点false是一动点,令false,false,false.
(1)若点false在线段false上,如图①所示,且false,则false_____false;
(2)若点false在边false上运动,如图②所示,则false、false、false之间的关系为______;
(3)如图③,若点false在斜边false的延长线上运动false,请写出false、false、false之间的关系式,并说明理由.
参考答案
1.C
【解答】多边形内角和定理.
【分析】设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),即可得方程180(n﹣2)=1080,
解此方程即可求得答案:n=8.故选C.
2.C
【解析】一个外角的度数是:180°-140°=40°,
则多边形的边数为:360°÷40°=9;
故选C.
【解答】
3.B
【解析】利用多边形的外角和是360°,正多边形的每个外角都是36°,即可求出答案.
【解答】解:360°÷36°=10,所以这个正多边形是正十边形.
故选B.
【点评】本题主要考查了多边形的外角和定理.是需要识记的内容.
4.A
【解答】多边形的内角和外角性质.
【分析】设此多边形是n边形,
∵多边形的外角和为360°,内角和为(n-2)180°,
∴(n-2)180=360,解得:n=4.
∴这个多边形是四边形.故选A.
5.D
【解析】四边形的外角和为360°,已知三个角的外角和,求出第四个角的外角度数,则得到第四个角的度数.
【解答】四边形第四个角的外角度数:360°-80°-85°-90°=105°
则第四个角是
180°-105°=75°
故答案选D.
【点评】本题考查多边形的内角和与外角和综合,理解多边形的外角和等于360°和多边形的外角与它相邻的内角互补是解题关键.
6.C
【解析】设多边形为n边形,由多边形的内角和定理列出方程求解即可.
【解答】解:设多边形为n边形.
由题意得:(n-2) ·180°=720°,
解得:n=6.
故选C.
【点评】本题考查多边形的内角和定理,n边形的内角和为:(n-2) ·180°.
7.C
【解答】由题意得(n-2)×180=360×2,解得n=6,
故选C.
8.D
【解答】试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)?180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
考点:多边形内角与外角.
9.D
【解析】根据两直线平行,内错角相等,得到∠DFA=∠CDB,根据三角形的内角和求出∠CDB的度数从而得到∠DFA的度数.
【解答】解:∠C=false,且CD=CB,
∴∠CDB=∠CBD
∵由三角形的内角和∠C+∠CDB+∠CBD=180°
∴∠CDB+∠CBD=180°-∠C =180°-108°=72°
∴∠CDB==∠CBD=false
又∵AF∥CD
∴∠DFA=∠CDB=36°(两直线平行,内错角相等)
故选D
【点评】本题主要考查多边形的基本概念和三角形的基本概念,正n边形的内角读数为false.
10.C
【解答】
设多边形原有边数为x,
则(2x?2)×180=2160,
2x?2=12,解得x=7,
故本题选C.
11.B
【解析】根据多边形的内角和定理与多边形外角的关系即可得出结论.
【解答】解:∵四边形的内角和等于a,
∴a=(4-2)?180°=360°.
∵五边形的外角和等于false,
∴false =360°,
∴a=false.
故选B.
【点评】本题考查的是多边形的内角与外角,熟知多边形的内角和定理是解答此题的关键.
12.D
【解答】设∠ADE=x,∠ADC=y,由题意可得,
∠ADE+∠AED+∠A=180°,∠A+∠B+∠C+∠ADC=360°,
即x+60+∠A=180①,3∠A+y=360②,
由①×3-②可得3x-y=0,
所以false,即∠ADE=false∠ADC.
故答案选D.
考点:三角形的内角和定理;四边形内角和定理.
13.C
【解析】
分析:根据边数求出各个多边形的每个内角的度数,结合镶嵌的条件列出方程,进而即可求出答案.
详解:由题意知,这3种多边形的3个内角之和为360度,已知正多边形的边数为x、y、z,那么这三个多边形的内角和可表示为:false+false+false=360,两边都除以180得:1﹣false+1﹣false+1﹣false=2,两边都除以2得:false+false+false=false.
故选C.
点睛:解决本题的关键是知道这3种多边形的3个内角之和为360度,据此进行整理分析得解.
14.C
【解析】根据多边形内角和公式false即可求出结果.
【解答】解:黑色正五边形的内角和为:false,
故选C.
【点评】本题考查了多边形的内角和公式,解题关键是牢记多边形的内角和公式.
15.A
【解析】利用多边形的外角和得出小明回到出发地false点时左转的次数,即可求出多边形的边数,即可解决问题.
【解答】解:由题意可知,小明第一次回到出发地false点时,他一共转了false,由题意得10°+20° +30°+40°+50°+60°+70°+80°=360°,所以共转了8次,每次沿直线前进10米,所以一共走了80米.
故选:A.
【点评】本题考查根据多边形的外角和解决实际问题,注意多边形的外角和是false,要注意第一次转了10°,第二次转了20°,第三次转了30°……,利用好规律解题.
16.A
【解析】根据多边形内角和定理:(n-2)·180(n≥3)且n为整数)的推导过程即可解答.
【解答】解:多边形内角和定理:(n-2)·180(n≥3)且n为整数),该公式推导的基本方法是从n边形的一个顶点出发引出(n-3)条对角线,将n边形分割为(n-2)个三角形,这(n-2)个三角形的所有内角之和正好是n边形的内角和,体现了化归思想.
故答案为A.
【点评】本题主要考查了在数学的学习过程应用的数学思想,弄清推导过程是解答此题的关键.
17.C
【解答】解:根据多边形的内角和公式(n-2)×180°,可以求得n=13.2,由于多加的是内角,
所以多加的角为小于180°的角,所以去掉小数部分就是n边形的边数.故选C
18.D
【解析】
【解析】正多边形的组合能否铺满地面,关键是要看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
【解答】解:A、正五边形和正三边形内角分别为108°、60°,由于60m+108n=360,得m=6-falsen,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;
B、正方形、正六边形内角分别为90°、120°,不能构成360°的周角,故不能铺满,故此选项错误;
C、正方形、正五边形内角分别为90°、108°,当90n+108m=360,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;
D、正五边形和正十边形内角分别为108、144,两个正五边形与一个正十边形能铺满地面,故此选项正确.
故选:D.
【点评】此题主要考查了平面镶嵌,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°-360°÷边数.
19.140°.
【解析】先根据多边形内角和定理:false求出该多边形的内角和,再求出每一个内角的度数.
【解答】解:该正九边形内角和false,
则每个内角的度数false.
故答案为140°.
【点评】本题主要考查了多边形的内角和定理:false,比较简单,解答本题的关键是直接根据内角和公式计算可得内角和.
20.40.
【解析】在DO延长线上找一点M,根据多边形的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【解答】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∴∠BOM=360°﹣220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°﹣∠BOM=180°﹣140°=40°.
故答案为:40
【点评】本题考查多边形的角度计算,关键在于熟记外角和360°.
21.5
【解析】设这个多边形的边数是n,则内角和为(n-2)×180°,故可列出方程求解.
【解答】设这个多边形的边数是n,则内角和为(n-2)×180°,
依题意得(n-2)×180°-360°=180°
解得n=5
故填:5.
【点评】此题主要考查多边形的内角和与外角和,解题的关键是熟知多边形的内角和与外角和公式.
22.false
【解答】解:由题意得,∠A的外角=180°-∠A=60°,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°-∠A的外角=300°.
故答案为:300.
【点评】本题考查多边形外角性质,补角定义.
23.30°.
【解答】解:∵AB//CD,∴∠BAC+∠ACD=180°,即∠1+∠EAC+∠ACD=180°,
∵五边形是正五边形,∴∠EAC=108°,
∵∠ACD=42°,∴∠1=180°-42°-108°=30°
故答案为:30°.
24.160.
【解析】
试题分析:该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数,即可求得周长,利用周长除以速度即可求得所需时间.
试题解析:360÷45=8,
则所走的路程是:6×8=48m,
则所用时间是:48÷0.3=160s.
考点:多边形内角与外角.
25.600
【解答】解:根据题意可知:小新从A点出发,沿直线前进50米后向左转30?,再沿直线前进50米,又向左转30?,……照这样下去,小新第一次回到出发地A点时,小新走的路线围成一个正多边形,且这个多边形的外角等于30?,所以这个正多边形的边数是12,小新一共走了12×50=600米,
故答案为:600.
26.8
【解析】
【解析】由一个正多边形的每个内角都为135°,可求得其外角的度数,继而可求得此多边形的边数,则可求得答案.
【解答】∵一个正n边形的每个内角都为135°,
∴这个正n边形的每个外角都为:180°-135°=45°,
∴这个n边形的边数为:360°÷45°=8,
故答案为:8.
【点评】此题考查了多边形的内角和与外角和的知识.此题难度不大,注意掌握多边形的内角和与外角和定理是关键.
27.false
【解析】
分析:求出正六边形的内角的度数,根据直角三角形的性质求出BG、CG,根据正多边形的性质计算.
详解:∵正六边形的每个内角=false,
则∠CBG=180°-120°=60°,
∴∠BCG=30°,
∴BG=falseBC=2,CG=falseBC=false,
∴AG=AB+BG=6,
∵四边形AGHI是正方形,
∴GH=AG=6,
∴CH=HG-CG=false,
故答案为false.
点睛:本题考查的是正多边形的有关计算,掌握正多边形的性质、内角的计算公式是解题的关键.
28.50°
【解析】过M作ME∥AB,AB∥ME∥CD,即可得到∠ABM+∠BMD+∠CDM=180°×2=360°,再根据false,
可得false,即可得到四边形BMDN中,∠N=360°﹣150°﹣160°=50°.
【解答】如图所示,过M作ME∥AB,则
∵AB∥CD,
∴AB∥ME∥CD,
∴∠ABM+∠BMD+∠CDM=180°×2=360°,
又∵∠BMD=160°,
∴∠ABM+∠CDM=200°,
又∵false,
∴false,
∴四边形BMDN中,∠N=360°﹣150°﹣160°=50°,
故答案为:50°.
【点评】本题主要考查了平行线的性质和四边形的内角和,解题的关键在于掌握两直线平行,同旁内角互补的性质.
29.8或9或10
【解析】先根据多边形的内角和公式(n﹣2)?180°求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
【解答】设多边形截去一个角的边数为n,根据题意得:
(n﹣2)?180°=1260°
解得:n=9.
∵截去一个角后边上可以增加1,不变,减少1,∴原多边形的边数是8或9或10.
故答案为8或9或10.
【点评】本题考查了多边形的内角和公式,本题难点在于多边形截去一个角后边数有增加1,不变,减少1三种情况.
30.10
【解析】首先求得正五边形围成的多边形的内角的度数,然后根据多边形的内角和定理即可求得答案.
【解答】解:正五边形的内角度数是:false=108°,
则正五边形围成的多边形的内角的度数是:360°?2×108°=144°,
根据题意得:180(n?2)=144n,
解得:n=10.
故答案为10.
【点评】本题考查了多边形的内角和定理,正确理解定理,求得围成的多边形的内角的度数是关键.
31.10°
【解答】试题分析:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:false(5﹣2)×180°=108°,则∠3=360°﹣60°﹣90°﹣108°﹣∠1﹣∠2=10°.故答案为10°.
考点:1.多边形内角与外角;2.三角形内角和定理.
32.30°
【解析】延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,根据BD是∠ABC的平分线可得出△BDE≌△BDF,故DE=DF,过D点作DG⊥AC于G点,可得出△ADE≌△ADG,△CDG≌△CDF,进而得出CD为∠ACF的平分线,得出∠DCA=53°,再根据三角形内角和定理即可得出结论.
【解答】解:
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,
∵BD是∠ABC的平分线
在△BDE与△BDF中,false ,
∴△BDE≌△BDF(ASA),
∴DE=DF,
又∵∠BAD+∠CAD=180°
∠BAD+∠EAD=180°
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
过D点作DG⊥AC于G点,
在Rt△ADE与Rt△ADG中,false ,
∴△ADE≌△ADG(HL),
∴DE=DG,
∴DG=DF.
在Rt△CDG与Rt△CDF中,false ,
∴Rt△CDG≌Rt△CDF(HL),
∴CD为∠ACF的平分线,
∠ACB=74°,
∴∠DCA=53°,
∴∠BDC=180°﹣∠CBD﹣∠DCA﹣∠ACB=180°﹣23°﹣53°﹣74°=30°.
故答案为:30°
【点评】本题考查了多边形的外角和内角,能熟记三角形的外角性质和三角形的内角和定理是解此题的关键,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和.
33.false
【解答】四边形有2条(false )对角线,五边形有5条(false)对角线,六边形有9条(false)对角线,故n边形有false条对角线.
故答案:false.
34.15 60°
【解析】设这个多边形边数是n,表示出一个外角的范围,求出不等式的解集确定出正整数n的值,即为多边形的边数,继而求出这个外角即可.
【解答】解:设这个多边形的边数是n,n为正整数,
根据题意得:0<2400°-(n-2)×180°<180°,
解得:14.3
故答案为:15;60°
【点评】本题考查了多边形内角与外角,熟练掌握内角和定理是解答此题的关键.
35.15.
【解析】设这个多边形的边数为false,依据多边形的内角和与外角和之比是false,即可得到false的值.
【解答】解:设这个多边形的边数为false,依题意得:
false,
解得false,
false这个多边形的边数为15.
【点评】考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,多边形的外角和等于360度.
36.这个多边形的边数是11,内角和度数是1620度.
【解答】试题分析:又多边形的外角和是360°,得到内角和是1620度.n边形的内角和可以表示成(n﹣2)?180°,设这个多边形的边数是n,就得到方程,从而求出边数.
试题解析:根据题意,得:(n﹣2)?180=1620,解得:n=11.则这个多边形的边数是11,内角和度数是1620度.
考点:多边形内角与外角.
37.(1) 这个多边形的边数是12边形;(2)这个多边形的边数为9.
【解析】(1)一个正多边形的每个内角比它相邻的外角的4倍还多30°,又由于内角与外角的和是180度.设内角是x°,外角是y°,列方程组求解;
(2)设这个多边形的边数为n,由n边形的内角和是(n-2)?180°,多边形的外角和是360°列出方程,解方程求出n的值即可.
【解答】(1)设内角是x°,外角是y°,
则得到一个方程组false
解得false.
而任何多边形的外角是360°,
则多边形内角和中的外角的个数是360÷30=12,
则这个多边形的边数是12边形;
(2)设这个多边形的边数为n,
依题意得:false(n-2)180°=360°,
解得n=9,
答:这个多边形的边数为9.
【点评】此题考查多边形内角与外角,正确的列出方程组是解题的关键.
38.(1)这个多边形是六边形;(2)这个多边形的每一个内角的度数是120°.
【解析】(1)先设内角为x,根据题意可得:外角为false,根据相邻内角和外角的关系可得:,x+false =180°,从而解得:x=120°,即外角等于60°,根据外角和等于360°可得这个多边形的边数为:false=6,
(2)先设内角为x,根据题意可得:外角为false,根据相邻内角和外角的关系可得:,x+false =180°,从而解得内角:x=120°,内角和=(6﹣2)×180°=720°.
【解答】(1)设内角为x,则外角为false,
由题意得,x+false =180°,
解得:x=120°,
false=60°,
这个多边形的边数为:false=6,
答:这个多边形是六边形,
(2)设内角为x,则外角为false,
由题意得: x+false =180°,
解得:x=120°,
答:这个多边形的每一个内角的度数是120度.
内角和=(6﹣2)×180°=720°.
【点评】本题主要考查多边形内角和外角,多边形内角和以及多边形的外角和,解决本题的关键是要熟练掌握多边形内角和外角的关系以及多边形内角和.
39.(1)270°;(2)220°;(3)∠1+∠2=180°+∠A ;(4)∠1+∠2=2∠A,理由见解析
【解析】(1)先求出∠B+∠C的度数,再根据四边形内角和等于360°,即可求解;
(2)先求出∠B+∠C的度数,再根据四边形内角和等于360°,即可求解;
(3)先用∠A表示出∠B+∠C,再根据四边形内角和等于360°,即可得到结论;
(4)由折叠的性质得∠AFE=∠PFE,∠AEF=∠PEF,结合平角的定义和三角形内角和定理,即可得到结论.
【解答】(1)∵△ABC为直角三角形,∠A=90°,
∴∠B+∠C=180°-90°=90°,
∴∠1+∠2=360°-(∠B+∠C)=270°.
故答案是:270°;
(2)∵△ABC中,∠A=40°,
∴∠B+∠C=180°-40°=140°,
∴∠1+∠2=360°-(∠B+∠C)=220°.
故答案是:220°;
(3)猜想:∠1+∠2=180°+∠A,理由如下:
∵△ABC中,∠B+∠C=180°-∠A,
∴∠1+∠2=360°-(∠B+∠C)=360°-(180°-∠A)=180°+∠A.
故答案是:∠1+∠2=180°+∠A;
(4)?∠1+∠2=2∠A,理由如下:
∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,
∴∠1+∠2=360°-2(∠AFE+∠AEF),
又∵∠AFE+∠AEF=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A.
【点评】本题主要考查三角形内角和定理,四边形内角和等于360°以及折叠的性质,熟练掌握三角形内角和定理,四边形内角和等于360°,是解题的关键.
40.(1)①证明见解析②若false,五边形false是正五边形(2)①真命题②真命题
【解析】(1)①用SSS证明false,得到false,即可得证;
②先证false,再证明false,再根据四边形的内角和与平行的性质证得false即可得证;
(2)①先证false,再举出等腰直角三角形的反例,得出false,由此即可得出结论;
②连接false、false、false,先证false,再证false,得到false,再由(2)①即可得出结论.
【解答】(1)①证明:∵凸五边形false的各条边都相等
∴false
在false、false、false、false、false中,false
∴false
∴false
∴五边形false是正五边形;
②解:若false,五边形false是正五边形,理由如下:
在false、false和false中,false
∴false
∴false,false
在false和false中,false
∴false
∴false,false
∵四边形false内角和为false
∴false
∴false
∴false,false
∴false
∴false
同理:false
∴五边形false是正五边形;
(2)解:①若false,则六边形false是正六边形;假命题,理由如下:
如图3所示,∵凸六边形false的各条边都相等
∴false
在false、false和false中,false
∴false
因此,如果false都为相同的等腰直角三角形,符合题意
但false,而正六边形的每个内角都为false
∴六边形false不是正六边形
故答案为:假;
②若false,则六边形false是正六边形;假命题;理由如下:
如图4所示:连接false、false、false
在false和false中,false
∴false
∴false
∵false
∴false
∴false
在false和false中,false
∴false
∴false
同理:false
∴false
由(2)①可知:六边形false不是正六边形
故答案为:假.
【点评】本题主要考查正多边形的证明,解题的关键是熟知全等三角形的判定与性质.
41.∠MON=33°.
【解析】由正方形、正五边形和正六边形的性质得到∠AOM=108°,∠OBC=120°,∠NBC=90°,求得∠AOB=false×120°=60°,∠MOB=108°-60°=48°,得到∠OBN=360°-120°-90°=150°,根据角和差即可得到结论.
【解答】解:如图,
由正方形、正五边形和正六边形的定义得:
∠AOM=108°,∠OBC= 120°,∠NBC =90°,
∴∠AOB=false120°=60°,∠MOB = 108° – 60°= 48°,
∴∠OBN= 360°- 120°- 90°= 150°,
∴∠NOB=false(180°-150°)=15°,
∴∠MON=48°-15°=33°.
【点评】本题考查了多边形的内角和外角,熟练掌握正方形、正五边形和正六边形的内角的度数是解题的关键.
42.(1)150°、120°、90°.(2)12.
【解析】(1)解答本题需要熟练掌握三角形内角和定理的知识,熟知三角形的内角和等于180°.通过解题,求出三个内角,再根据内角加对应的外交和等于180°算出外角;
(2)根据多边形内角和即可求出.
【解答】(1)设此三角形三个内角的比为x,2x,3x,
则x+2x+3x=180,
6x=180,
x=30,
则三个内角分别为30°、60°、90°,
相应的三个外角分别为150°、120°、90°.
(2)设这个多边形的边数是n,
则(n﹣2)?180°=1800°,
解得n=12.
故这个多边形的边数为12.
【点评】本题考查的知识点是多边形内角和,解题的关键是熟练的掌握多边形内角和.
43.(1)见解析;(2)∠P=23?;(3)∠P=26?;(4)∠P=false;(5)∠P=false.
【解析】(1)根据三角形内角和定理即可证明;
(2)如图2,根据角平分线的性质得到∠1=∠2,∠3=∠4,列方程组即可得到结论;
(3)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°-∠2,∠PCD=180°-∠3,由∠P+(180°-∠1)=∠D+(180°-∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解决问题;
(4)根据题意得出∠B+∠CAB=∠C+∠BDC,再结合∠CAP=false∠CAB,∠CDP=false∠CDB,得到y+(∠CAB-false∠CAB)=∠P+(∠BDC-false∠CDB),从而可得∠P=y+∠CAB-false∠CAB-∠CDB+false∠CDB=false;
(5)根据题意得出∠B+∠BAD=∠D+∠BCD,∠DAP+∠P=∠PCD+∠D,再结合AP平分∠BAD,CP平分∠BCD的外角∠BCE,得到false∠BAD+∠P=[∠BCD+false(180°-∠BCD)]+∠D,所以∠P=90°+false∠BCD-false∠BAD +∠D=false.
【解答】解:(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)解:如图2,∵AP、CP分别平分∠BAD,∠BCD,
∴∠1=∠2,∠3=∠4,
由(1)的结论得:false,
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D,
∴∠P=false(∠B+∠D)=23°;
(3)解:如图3,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°-∠2,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠D+(180°-∠3),
∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=false(∠B+∠D)=false×(36°+16°)=26°;
故答案为:26°;
(4)由题意可得:∠B+∠CAB=∠C+∠BDC,
即y+∠CAB=x+∠BDC,即∠CAB-∠BDC=x-y,
∠B+∠BAP=∠P+∠PDB,
即y+∠BAP=∠P+∠PDB,
即y+(∠CAB-∠CAP)=∠P+(∠BDC-∠CDP),
即y+(∠CAB-false∠CAB)=∠P+(∠BDC-false∠CDB),
∴∠P=y+∠CAB-false∠CAB-∠CDB+false∠CDB
= y+false(∠CAB-∠CDB)
=y+false(x-y)
=false
故答案为:∠P=false;
(5)由题意可得:∠B+∠BAD=∠D+∠BCD,
∠DAP+∠P=∠PCD+∠D,
∴∠B-∠D=∠BCD-∠BAD,
∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠BAP=∠DAP,∠PCE=∠PCB,
∴false∠BAD+∠P=(∠BCD+false∠BCE)+∠D,
∴false∠BAD+∠P=[∠BCD+false(180°-∠BCD)]+∠D,
∴∠P=90°+false∠BCD-false∠BAD +∠D
=90°+false(∠BCD-∠BAD)+∠D
=90°+false(∠B-∠D)+∠D
=false,
故答案为:∠P=false.
【点评】本题考查三角形内角和,三角形的外角的性质、多边形的内角和等知识,解题的关键是学会用方程组的思想思考问题,属于中考常考题型.
44.∠COD=100°
【解析】由于∠A+∠B=200°,根据四边形的内角和定理求出∠ADC+∠DCB的度数,然后根据角平分线的定义得出∠ODC+∠OCD的度数,最后根据三角形内角和定理求出∠COD的度数.
【解答】解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°﹣200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=false∠ADC,∠OCD=false∠BCD,
∴∠ODC+∠OCD=false×160°=80°,
∴∠COD=180°﹣80°=100°.
【点评】本题主要考查了三角形及四边形的内角和定理.三角形的内角和等于180°;四边形的内角和等于360°.
45.(1)140°;(2)∠1+∠2=90°+α.(3)如图1,∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠1?∠2=∠α?90°.
【解析】(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质分三种情况讨论即可.
【解答】(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°;
(2)由(1)得出:∠α+∠C=∠1+∠2,∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点,如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,∴∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠2=∠1?∠α+∠C,∴∠1?∠2=∠α?90°.
【点评】本题考查三角形内角和定理和外角的性质、对顶角相等的性质和四边形内角和定理,熟练利用三角形外角的性质是解决问题的关键.
