13.2:画轴对称图形 同步提高课时练习(含解析)
文档属性
| 名称 | 13.2:画轴对称图形 同步提高课时练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 18:48:50 | ||
图片预览


文档简介
13.2:画轴对称图形
一、单选题
1.如图,把false经过一定的变换得到false,如果false上点false的坐标为false,那么这个点在false中的对应点false的坐标为( )
A.false B.false C.false D.false
2.将点P(-2,3)向右平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是( )
A.(-5,-3) B.(1,-3) C.(-1,-3) D.(5,-3)
3.如图,点A的坐标(﹣1,2),点A关于y轴的对称点的坐标为( )
A.(1,2) B.(﹣1,﹣2) C.(1,﹣2) D.(2,﹣1)
4.若点A(1﹣m,2)与点B(﹣1,n)关于y轴对称,则m+n=( )
A.2 B.0 C.﹣2 D.﹣4
5.平面直角坐标系中,与点false关于y轴对称的点是( )
A.false B.false C.false D.false
6.点A(﹣3,2)关于x轴的对称点A′的坐标为( )
A.(3,2) B.(3,﹣2) C.(﹣3,2) D.(﹣3,﹣2)
7.将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,顺次连接这三个点,得到另一个三角形,下列选项正确的是( )
A. B. C. D.
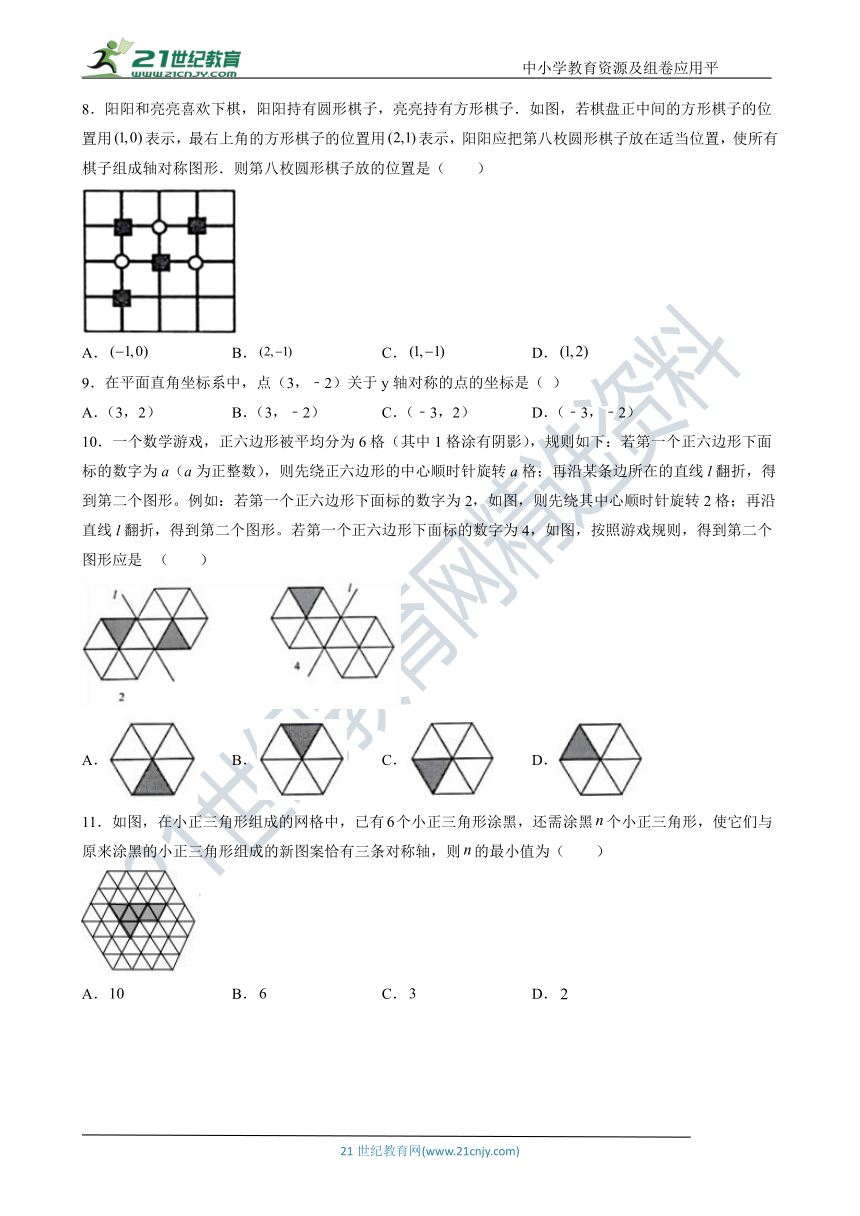
8.阳阳和亮亮喜欢下棋,阳阳持有圆形棋子,亮亮持有方形棋子.如图,若棋盘正中间的方形棋子的位置用false表示,最右上角的方形棋子的位置用false表示,阳阳应把第八枚圆形棋子放在适当位置,使所有棋子组成轴对称图形.则第八枚圆形棋子放的位置是( )
A.false B.false C.false D.false
9.在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是( )
A.(3,2) B.(3,﹣2) C.(﹣3,2) D.(﹣3,﹣2)
10.一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形。例如:若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l翻折,得到第二个图形。若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是false( )
A. B. C. D.
11.如图,在小正三角形组成的网格中,已有false个小正三角形涂黑,还需涂黑false个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则false的最小值为( )
A.false B.false C.false D.false
12.如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画( )条线段.
A.1 B.2 C.3 D.4
13.已知在平面直角坐标系中,点A的坐标为(﹣3,4),下列说法正确的有( )个
①点A与点B(-3,﹣4)关于x轴对称
②点A与点C(3,﹣4)关于原点对称
③点A与点F(-4,3)关于第二象限的平分线对称
④点A与点C(4,-3)关于第一象限的平分线对称
A.1 B.2 C.3 D.4
14.点false关于false轴的对称点false坐标为( )
A.false B.false C.false D.false
15.点false经过某种图形变换后得到点false这种图形变换可以是( )
A.关于false轴对称 B.关于false轴对称
C.绕原点逆时针旋转false D.绕原点顺时针旋转false
16.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
A.3cm B.4cm C.5cm D.6cm
17.如图,等边false的顶点false,false,规定把false“先沿false轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边false的顶点false的坐标为( )
A.false B.false C.false D.false
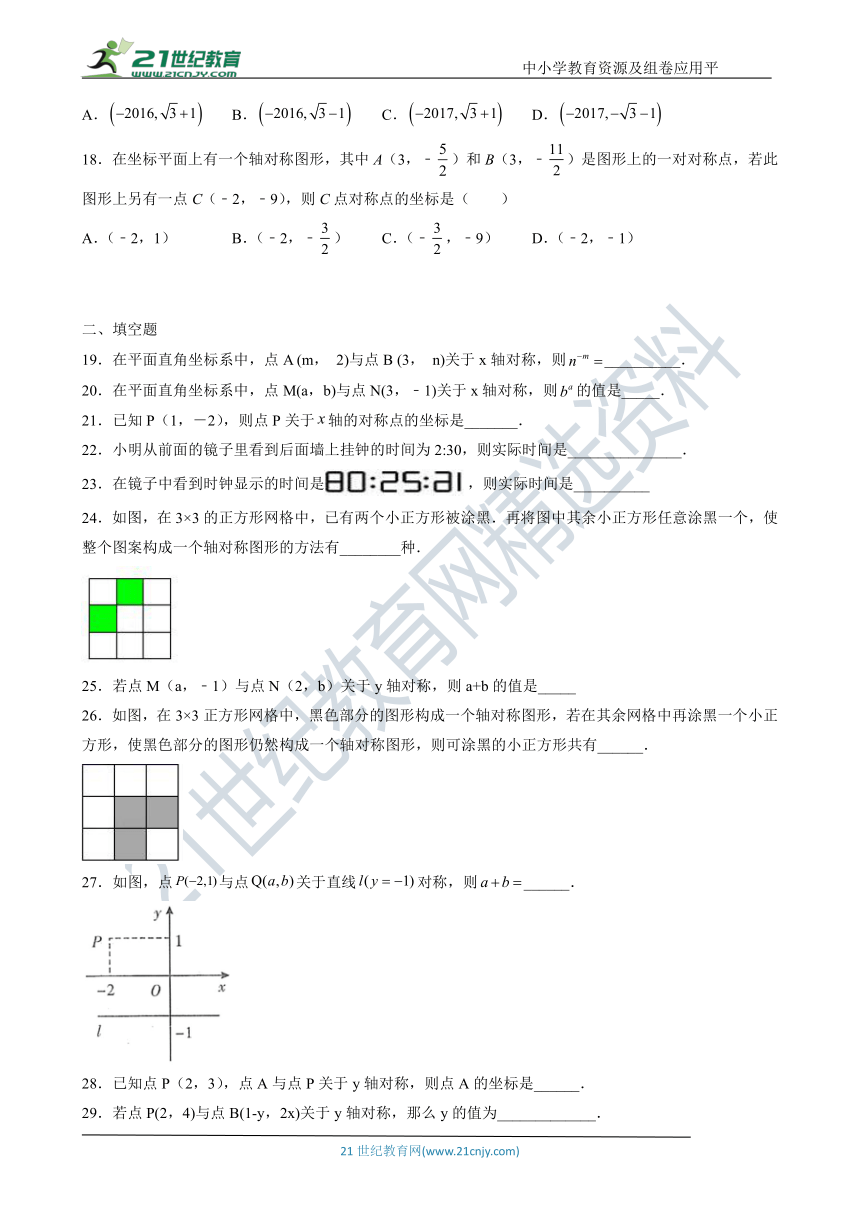
18.在坐标平面上有一个轴对称图形,其中A(3,﹣false)和B(3,﹣false)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1) B.(﹣2,﹣false) C.(﹣false,﹣9) D.(﹣2,﹣1)
二、填空题
19.在平面直角坐标系中,点A (m, 2)与点B (3, n)关于x轴对称,则false__________.
20.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则false的值是_____.
21.已知P(1,-2),则点P关于false轴的对称点的坐标是_______.
22.小明从前面的镜子里看到后面墙上挂钟的时间为2:30,则实际时间是_______________.
23.在镜子中看到时钟显示的时间是,则实际时间是__________
24.如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有________种.
25.若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是_____
26.如图,在3×3正方形网格中,黑色部分的图形构成一个轴对称图形,若在其余网格中再涂黑一个小正方形,使黑色部分的图形仍然构成一个轴对称图形,则可涂黑的小正方形共有______.
27.如图,点false与点false关于直线false对称,则false______.
28.已知点P(2,3),点A与点P关于y轴对称,则点A的坐标是______.
29.若点P(2,4)与点B(1-y,2x)关于y轴对称,那么y的值为_____________.
30.已知点A(x,-4)与点B(3,y)关于x轴对称,那么x+y的值为____________.
31.已知false(a?1,5)和false(2,b?1)关于x轴对称,则false的值为 _________ .
32.点false关于false轴的对称点的坐标为______.
33.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出_____个格点三角形与△ABC成轴对称.
34.如图,在false中,点A的坐标为false,点B的坐标为false,点C的坐标为false,点D在第二象限,且false与false全等,点D的坐标是______.
三、解答题
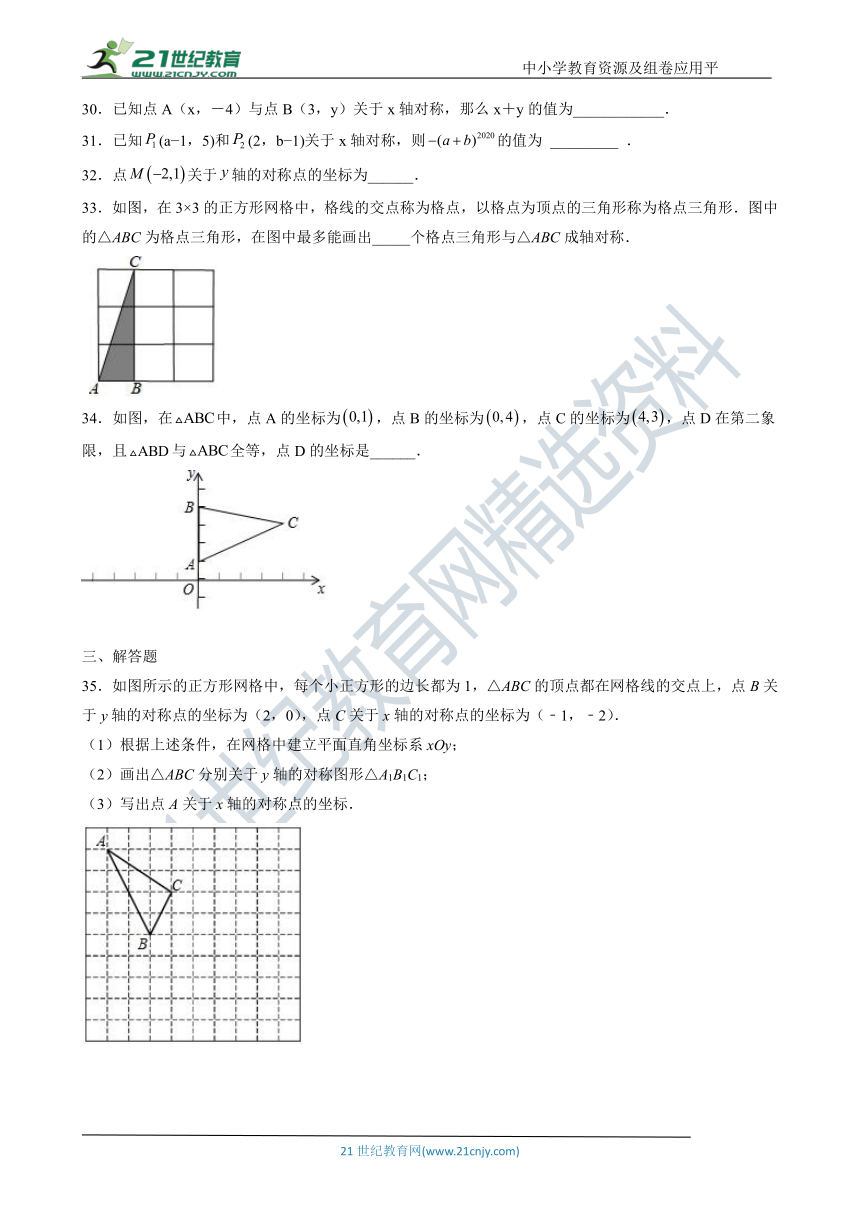
35.如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在网格线的交点上,点B关于y轴的对称点的坐标为(2,0),点C关于x轴的对称点的坐标为(﹣1,﹣2).
(1)根据上述条件,在网格中建立平面直角坐标系xOy;
(2)画出△ABC分别关于y轴的对称图形△A1B1C1;
(3)写出点A关于x轴的对称点的坐标.
36.如图,已知false各顶点的坐标分别为false,false,false,直线false经过点false,并且与false轴平行,false与false关于直线false对称.
(1)画出false,并写出点false的坐标 .
(2)若点false是false内一点,点false是false内与点false对应的点,则点false坐标 .
37.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.
38.在平面直角坐标系false中,已知false,false,false三点的坐标.
(1)写出点false关于原点false的对称点false的坐标,点false关于false轴的对称点false的坐标,点false关于false轴的对称点false的坐标;
(2)求(1)中的false的面积.
39.在平面直角坐标系中,已知点A(x,y),点B(x﹣my,mx﹣y)(其中m为常数,且m≠0),则称B是点A的“m族衍生点”.例如:点A(1,2)的“3族衍生点”B的坐标为(1﹣3×2,3×1﹣2),即B(﹣5,1).
(1)点(2,0)的“2族衍生点”的坐标为 ;
(2)若点A的“3族衍生点”B的坐标是(﹣1,5),则点A的坐标为 ;
(3)若点A(x,0)(其中x≠0),点A的“m族衍生点“为点B,且AB=OA,求m的值;
(4)若点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,则点A的位置在 .
40.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,false的顶点都在格点上,点false的坐标false,点false,点false.
(1)false将沿false轴向上平移3个单位得到false,画出false,并写出false的坐标.
(2)画出false关于false轴对称的false.
41.如图,在平面直角坐标系xOy中,A(-3,4),B(-4,1),C(-1,1).
(1)在图中作出△ABC关于x轴的轴对称图形△A′B′C′;
(2)直接写出A,B关于y轴的对称点A″,B″的坐标.
42.如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
43.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点和(顶点为网格线的交点),以及过格点的直线.
(1)将向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形;
(2)画出关于直线对称的三角形;
(3)填空: .
44.如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________
45.在直角坐标系中,false的三个顶点都在边长为false的小正方形的格点上,关false于false轴的对称图形为false,以false与false组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
(1)观察以上图形并填写下列各点坐标:
false,false,false,false(false为正整数)
(2)若false是这组图形中的一个三角形,当false时,则false ,false
参考答案
1.B
【解析】先观察△ABC和△A′B′C′得到把△ABC向上平移2个单位,再关于y轴对称可得到△A′B′C′,然后把点P(x,y)向上平移2个单位,再关于y轴对称得到点的坐标为(-x,y+2),即为P′点的坐标.
【解答】解:∵把△ABC向上平移2个单位,再关于y轴对称可得到△A′B′C′,
∴点P(x,y)的对应点P′的坐标为(-x,y+2).
故选:B.
【点评】本题考查了坐标与图形变化,解决本题的关键是根据已知对应点找到各对应点之间的变化规律.
2.C
【解答】解:∵点P(-2,3)向右平移3个单位得到点false,∴false,
∵点false与点false关于原点对称,∴false
故选C.
3.A
【解答】分析:直接利用关于y轴对称点的性质分析得出答案.
详解:点A的坐标(﹣1,2),点A关于y轴的对称点的坐标为:(1,2).
故选A.
点睛:此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.A
【解析】根据关于y轴的对称点的坐标特点可得m、n的值,进而可得m+n的值.
【解答】∵点A(1﹣m,2)与点B(﹣1,n)关于y轴对称,
∴1﹣m=1,n=2,
解得:m=0,n=2,
∴m+n=2,
故选:A.
【点评】本题主要考查了关于y轴的对称点的坐标特点,关键是掌握关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变.
5.C
【解析】根据平面直角坐标系中任意一点P(x,y),关于y轴对称的点的坐标为(-x,y),所此可得出答案.
【解答】根据关于x轴、y轴对称的点的坐标的特点,
∴点(2,-3)关于y轴对称的点的坐标是(-2,-3).
故选:C.
【点评】本题主要考查了平面直角坐标系中关于y轴对称的点的坐标的特点,注意掌握任意一点P(x,y),关于x轴的对称点的坐标是(x,-y),关于y轴对称的点的坐标为(-x,y),比较简单.
6.D
【解析】直接利用关于x轴对称点的性质得出符合题意的答案.
【解答】解:点A(﹣3,2)关于x轴的对称点A′的坐标为:(﹣3,﹣2),
故选:D.
【点评】本题考查了关于x轴对称的点的坐标特征,关于x轴对称的点:横坐标不变,纵坐标互为相反数.
7.A
【解析】根据将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,可得出对应点关于y轴对称,进而得出答案.
【解答】解:∵将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,顺次连接这三个点,得到另一个三角形,
∴对应点的坐标关于y轴对称,只有选项A符合题意.
故选A.
【点评】此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标变化与坐标轴的关系是解题关键.
8.C
【解析】本题考查平面直角坐标系的应用,需要根据题干已给具体坐标确定坐标系的原点所在,同时需要按照轴对称图形要求求解本题.
【解答】根据坐标(1,0),(2,1)可确定平面直角坐标系原点位于图形中最左边的圆形棋子处,按照轴对称图形要求,第八枚棋子应该放于左下方方形棋子的右边一格,即坐标(1,-1)
故答案为:C.
【点评】本题考查坐标系方式较为新颖,需要熟练掌握平面直角坐标系的象限特点,采取逆向思维求解本题.
9.D
【解答】试题分析:点(3,﹣2)关于y轴对称的点的坐标是(﹣3,﹣2)故选D.
考点:关于x轴、y轴对称点的坐标.
10.A
【解析】
试题解析:第一个正六边形下面标的数字为4,先绕其中心顺时针旋转4格,
旋转后的图形是,关于直线false的对称图形是.
故选A.
11.C
【解析】由等边三角形有三条对称轴可得答案.
【解答】如图所示,n的最小值为3.
故选C.
【点评】本题考查了利用轴对称设计图案,解题的关键是掌握常见图形的性质和轴对称图形的性质.
12.D
【解析】由轴对称图形的性质画出满足条件的所有线段即可.
【解答】如图:画出的线段有CD、DE、FG、HI,共4条.
故选D.
【点评】本题主要考查轴对称图形的性质.
13.D
【解析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数;关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变;关于第2象限角平分线对称的点的坐标特点:横纵坐标变换位置且变为相反数;关于第1象限角平分线对称的点的坐标特点:横纵坐标变换位置.综合以上即可得答案.
【解答】∵点A的坐标为(﹣3,4),
∴点A关于x轴对称的点的坐标为(﹣3,﹣4),
点A关于原点对称的点的坐标为(3,-4),
点A关于第二象限的角平分线对称的点的坐标为(-4,3)
点A关于第一象限的角平分线对称的点的坐标为(4,-3)
∴①、②、③、④正确.
故选:D.
【点评】此题主要考查了关于x轴、y轴、第二象限的角平分线、第一象限的角平分线对称的点的坐标规律,关键是熟练掌握点的变化规律,不要混淆.
14.A
【解析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答.
【解答】点A(2,1)关于x轴的对称点是(2,-1).
故选:A.
【点评】此题考查关于x轴、y轴对称的点的坐标,解题的关键是掌握好对称点的坐标规律.
15.A
【解析】直接利用利用关于x轴对称点的性质得出答案.
【解答】∵点(4,3)经过某种图形变化后得到点B(4,-3),
∴这种图形变化可以是关于x轴对称.
故选:A.
【点评】此题主要考查了关于x轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
16.C
【解析】
试题分析:根据轴对称的性质可得PM=P1M,PN=P2N,然后求出△PMN的周长=P1P2.
解:∵P点关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2,
∵△PMN的周长是5cm,
∴P1P2=5cm.
故选C.
考点:轴对称的性质.
17.D
【解析】先求出点C坐标,第一次变换,根据轴对称判断出点C变换后在x轴下方然后求出点C纵坐标,再根据平移的距离求出点C变换后的横坐标,最后写出第一次变换后点C坐标,同理可以求出第二次变换后点C坐标,以此类推可求出第n次变化后点C坐标.
【解答】∵△ABC是等边三角形AB=3-1=2
∴点C到x轴的距离为1+false,横坐标为2
∴C(2,false)
由题意可得:第1次变换后点C的坐标变为(2-1,false),即(1,false),
第2次变换后点C的坐标变为(2-2,false),即(0,false)
第3次变换后点C的坐标变为(2-3,false),即(-1,false)
第n次变换后点C的坐标变为(2-n,false)(n为奇数)或(2-n,false)(n为偶数),
∴连续经过2019次变换后,等边false的顶点false的坐标为(-2017,false),
故选:D
【点评】本题考查了利用翻折变换和平移的特点求解点的坐标,在求解过程中找到规律是关键.
18.A
【解析】先利用点A和点B的坐标特征可判断图形的对称轴为直线y=-4,然后写出点C关于直线y=-4的对称点即可.
【解答】解:∵A(3,﹣false)和B(3,﹣false)是图形上的一对对称点,
∴点A与点B关于直线y=﹣4对称,
∴点C(﹣2,﹣9)关于直线y=﹣4的对称点的坐标为(﹣2,1).
故选:A.
【点评】本题考查了坐标与图形的变化,需要注意关于直线对称:关于直线x=m对称,则两点的纵坐标相同,横坐标和为2m;关于直线y=n对称,则两点的横坐标相同,纵坐标和为2n.
19.false
【解析】直接利用关于x轴对称的点的性质得出m,n的值,进而得出答案.
【解答】解:∵点A (m, 2)与点B (3, n)关于x轴对称,
∴m=3,n=-2,
∴false.
故答案为:false.
【点评】此题主要考查了关于x轴对称的点的特征,熟记特征是解题关键.
20.1
【解析】根据关于x轴对称的两点的横坐标相同,纵坐标互为相反数求得a、b的值即可求得答案.
【解答】解:在直角坐标系中,关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
∴false=1,
故答案为:1.
【点评】本题考查了关于x轴对称的点的坐标特征,熟练掌握关于坐标轴对称的点的坐标特征是解题的关键.
21.(1,2)
【解答】解:关于x轴对称的点的坐标特征是横坐标相同,纵坐标互为相反数,
从而点P(1,-2)关于x轴对称的点的坐标是(1,2)
故答案为:(1,2)
【点评】本题考查关于x轴对称的点的坐标特征.
22.9:30
【解析】利用镜面对称的性质求解.镜面对称的性质:在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.
【解答】解:false时,分针竖直向下,时针指2和3之间,根据对称性可得:与false时的指针指向成轴对称,故实际时间是false.
【点评】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
23.16:25:08.
【解答】试题分析:∵实际时间和镜子中的时间关于竖直的线成轴对称,∴实际时间是16:25:08,
故答案为16:25:08.
考点:镜面对称.
24.5 种
【解析】根据轴对称图形的性质分别得出即可.
【解答】如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形.选择一个正方形涂黑,使得3个涂黑的正方形组成轴对称图形,选择的位置有以下几种:1,3,7,6,5,选择的位置共有5处.
25.-3
【解析】
试题解析:∵点M(a,﹣1)与点N(2,b)关于y轴对称,
∴a=﹣2,b=﹣1,
∴a+b=(﹣2)+(﹣1)=﹣3.
故答案为﹣3.
26.4.
【解析】直接利用轴对称图形的性质分析得出答案.
【解答】如图所示:当在空白处1到4个数字位置涂黑时,使黑色部分的图形仍然构成一个轴对称图形.
故答案为:4.
【点评】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
27.-5
【解析】根据点false与点false关于直线false对称求得a,b的值,最后代入求解即可.
【解答】解:∵点false与点false关于直线false对称
∴a=-2,false,解得b=-3
∴a+b=-2+(-3)=-5
故答案为-5.
【点评】本题考查了关于y=-1对称点的性质,根据对称点的性质求得a、b的值是解答本题的关键.
28.(-2,3)
【解析】
点P(2,3),点A与点P关于y轴对称,则点A的坐标是(?2,3),
故答案为(?2,3).
29.3
【解析】点P关于y轴对称,根据轴对称特点可解.
【解答】∵点P(2,4)与点B(1-y,2x)关于y轴对称,那么点P和点B横坐标数值互为相反数.
∴false
∴false
故答案为:3.
【点评】本题考查了坐标与图形变化-轴对称,熟练掌握轴对称坐标特点是解题的关键.
30.7
【解析】关于x轴对称,x不变,y变号,根据这个知识即可.
【解答】解:点A(x,-4)与点B(3,y)关于选轴对称,
所以有y=4,
x=3,
即x+y=7;
考查了学生对点关于坐标轴对称问题认识:
关于y轴对称,y不变,x变号;
关于x轴对称,x不变,y变号.
31.-1
【解析】根据两点关于x轴对称的坐标的关系,得a﹣1=2,b﹣1=﹣5,求出a,b的值,进而即可求解.
【解答】∵false 和false 关于x轴对称,
∴false
解得:false ,
∴false.
故答案为:﹣1.
【点评】本题主要考查平面直角坐标系中,两点关于x轴对称坐标的关系,掌握两点关于x轴对称,横坐标相等,纵坐标互为相反数,是解题的关键.
32.false
【解析】关于y轴对称的点,纵坐标相同,横坐标互为相反数.
【解答】∵关于y轴对称的点,纵坐标相同,横坐标互为相反数
∴点false关于y轴的对称点的坐标为false.
故答案为:false
【点评】考核知识点:轴对称与点的坐标.理解轴对称和点的坐标关系是关键.
33.6
【解析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解.
【解答】如图,最多能画出6个格点三角形与△ABC成轴对称.
故答案为:6.
【点评】本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.
34.(-4,2)或(-4,3)
【解答】把点C向下平移1个单位得到点D(4,2),这时△ABD与△ABC全等,分别作点C,D关于y轴的对称点(-4,3)和(-4,2),所得到的△ABD与△ABC全等.
故答案为(-4,2)或(-4,3).
35.(1)详见解析;(2)详见解析;(3)(-4,-4).
【解析】(1)依据点B关于y轴的对称点坐标为(2,0),点C关于x轴的对称点坐标为(-1,-2),即可得到坐标轴的位置;
(2)依据轴对称的性质,即可得到△ABC分别关于y轴的对称图形△A1B1C1;
(3)依据关于x轴的对称点的横坐标相同,纵坐标互为相反数,即可得到点A关于x轴的对称点的坐标.
【解答】解:(1)如图所示,建立平面直角坐标系xOy.
(2)如图所示,△A1B1C1即为所求;
(3)A点关于x轴的对称点的横坐标相同,纵坐标互为相反数,所以点A(-4,4)关于x轴的对称点的坐标(-4,-4).
【点评】本题主要考查作图?轴对称变换,解题的关键是熟练掌握轴对称变换的定义和性质.
36.(1) (1,2) ; (2) false.
【解析】(1)根据轴对称的性质找到各点的对应点,然后顺次连接即可,画出图形即可直接写出坐标.
(2)根据轴对称的性质可以直接写出false.
【解答】(1)如图所示:
直接通过图形得到false(1,2)
(2) 由题意可得:由于false与false 关于x=-1 对称
所以false.
【点评】此题主要考查了轴对称作图的知识,注意掌握轴对称的性质,找准各点的对称点是关键.
37.(1)见解析;(2) 见解析.
【解析】(1)利用△ABC三边长度,画出以A1为顶点的三角形三边长度即可,利用图象平移,可得出△A1B1C1.
(2)利用点B关于直线AC的对称点D,得出D点坐标,根据勾股定理和逆定理可得出AD与AB的位置关系.
【解答】(1)如图:
(2)∵AB=false,AD=false,BD=false,
∴AB2+AD2=BD2.
∴△ABD是直角三角形.
∴AD可以看作由AB绕A点逆时针旋转90°得到的.
【点评】本题考查了作图(平移变换、轴对称变换),全等图形,旋转和轴对称的性质,勾股定理和逆定理,图形变换有两种,全等变换和相似变换,掌握每种变换的概念、性质是作图的基础,一般难度不大.
38.(1) A′的坐标为(1,?5), B′的坐标为(4,?2), C′的坐标为(1,0);(2)false.
【解析】(1)根据点关于原点对称、关于x轴的对称和关于y轴对称的点的坐标特征求解;
(2)利用三角形面积公式求解.
【解答】(1)点A关于原点O的对称点A′的坐标为(1,?5),点B关于x轴的对称点B′的坐标为(4,?2),点C关于y轴的对称点C′的坐标为(1,0).
(2)以A′C′为底边,B′D为高,可得:△A′B′C′的面积=false×5×3=false.
【点评】此题考查坐标与图形-对称轴变换,解题关键在于掌握运算公式.
39.(1)(2,4);(2)(2,1);(3)m=±1;(4)y轴上
【解析】(1)利用“m族衍生点”的定义可求解;
(2)设点A坐标为(x,y),利用“m族衍生点”的定义列出方程组,即可求解;
(3)先求出点A的“m族衍生点“为点B(x,mx),由AB=OA,可求解;
(4)先求出点A(x,y)的“m族衍生点”为(x﹣my,mx﹣y),点A(x,y)的“﹣m族衍生点”为(x+my,﹣mx﹣y),由轴对称的性质可求x=0,即可求解.
【解答】解:(1)点(2,0)的“2族衍生点”的坐标为(2﹣2×0,2×2﹣0),即(2,4),
故答案为(2,4);
(2)设点A坐标为(x,y),
由题意可得:false,
∴false,
∴点A坐标为(2,1);
(3)∵点A(x,0),
∴点A的“m族衍生点“为点B(x,mx),
∴AB=|mx|,
∵AB=OA,
∴|x|=|mx|,
∴m=±1;
(4)∵点A(x,y),
∴点A(x,y)的“m族衍生点”为(x﹣my,mx﹣y),点A(x,y)的“﹣m族衍生点”为(x+my,﹣mx﹣y),
∵点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,
∴false,
∴x=0,
∴点A在y轴上,
故答案为:y轴上.
【点评】本题主要考查新定义问题,平面直角坐标系中关于y轴对称的点的坐标特征,二元一次方程组的解法,准确根据题意解题是关键.
40.(1)作图见详解,B1的坐标为(﹣2,﹣1);(2)见详解
【解析】(1)直接利用平移的性质分别得出对应点位置进而得出答案;
(2)直接利用关于y轴对称点的性质得出对应点位置进而得出答案.
【解答】解:(1)如图,△A1B1C1为所作,点B1的坐标为(﹣2,﹣1);
(2)如图,△A2B2C2为所作.
【点评】此题主要考查了平移变换以及轴对称变换,正确得出对应点位置是解题关键.
41.(1)见解析;(2)A″(3,4),B″(4,1).
【解析】(1)正确找出对应点A′,B′,C′即可得出△ABC关于x轴的轴对称图形△A′B′C′;
(2)根据关于y轴对称的点,纵坐标不变,横坐标改变符号直接写出即可.
【解答】(1)如图所示;
(2)点A(﹣3,4)、B(﹣4,1)关于y轴的对称点A″、B″的坐标分别为:A″(3,4),B″(4,1).
【点评】本题考查轴对称图形的作法以及关于坐标轴对称的点的坐标特点,灵活应用关于坐标轴对称的点的性质是解题的关键.
42.(1)14cm;(2)36°.
【解析】(1)折叠时,对称轴为折痕DE,DE垂直平分线段AB,由垂直平分线的性质得DA=DB,再把△ACD的周长进行线段的转化即可;
(2)设∠CAD=x,则∠BAD=2x,根据(1)DA=DB,可证∠B=∠BAD=2x,在Rt△ABC中,利用互余关系求x,再求∠B.
【解答】(1)由折叠的性质可知,DE垂直平分线段AB,
根据垂直平分线的性质可得:DA=DB,
所以,DA+DC+AC=DB+DC+AC=BC+AC=14cm;
(2)设∠CAD=x,则∠BAD=2x,
∵DA=DB,
∴∠B=∠BAD=2x,
在Rt△ABC中,∠B+∠BAC=90°,
即:2x+2x+x=90°,x=18°,
∠B=2x=36°.
【点评】考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.
43.(1)见解析;(2)见解析;(3)45
【解答】试题分析:(1)画一个图形的平移后的图形;(2)画出已知图形关于某直线对称的图形;(3)构造直角三角形即可.
试题解析:(1)如图所示;(2)如图所示;(3)45
考点: 作已知图形按照一定规则平移后的图形,及关于某直线成轴对称的图形.
44.(1)20;(2)80°;(3)∠EPF= 180°-2∠O
【解析】(1)根据轴对称的性质可得EM=EP,FP=FN,进而推出MN=EM+EF+FN=EP+EF+FP=△PEF的周长即可;
(2)由(1)及等腰三角形的性质、四边形的内角和找出∠M+∠N与∠O、∠EPF与∠O的关系即可;
(3)由(2)可直接得到∠EPF= 180°-2∠O.
【解答】解:(1)∵点M、N分别是点P关于AO、BO所在直线的对称点.
∴OA垂直平分PM,OB垂直平分PN,
∴EM=EP,FP=FN,
∴MN=EM+EF+FN=EP+EF+FP=△PEF的周长,
又∵△PEF的周长为20,
∴MN=20 cm.
(2)由(1)知:EM=EP,FP=FN,
∴∠PEF=2∠M,∠PFE=2∠N,
∵∠PCE=∠PDF=90°,
∴在四边形OCPD中,∠CPD+∠O=180°,
又∵在△PMN中,∠MPN+∠M+∠N=180°,且∠CPD+∠O=180°,
∴∠M+∠N=∠O=50°.
∴在△PEF中,∠EPF +∠PEF+∠PFE=∠EPF +2∠M +2∠N =180°,
即∠EPF=180°-2∠M -2∠N =180°-2(∠M +∠N)= 180°-2∠O=80°.
(3)由(2)可直接得到∠EPF= 180°-2∠O.
故答案为:∠EPF= 180°-2∠O.
【点评】本题主要考查轴对称的性质、四边形的内角和、等腰三角形的性质等,准确掌握轴对称性质的核心进行推理计算是解题的关键.
45.(1)false;false;false;(2)false,false.
【解析】(1)结合图形,先写出false、false的坐标,然后结合图形可发现规律,false,false,false的横坐标依次多4,纵坐标没变从而可得false的坐标;
false找出图中A、B、C的角码变化规律,然后根据false可得m、k得到值.
【解答】解:(1)由图可得false,false,false,
由图可得false,false,false的纵坐标不变,横坐标多一个就多4,
false的坐标为false,即false,
故答案为2,2;6,2;false,2;
(2)因为false,所以当n为奇数时,
由图可得,false对应false,false对应false,false对应false,false对应false,
false对应false,故当false时,false;
false对应C,B3对应false,false对应false,false,
false对应false,故当false时,false,
故答案为1010,1009.
【点评】本题主要考查了轴对称与坐标的变化关系,解答此题的关键是弄清向右翻折只变横坐标,纵坐标不变.
一、单选题
1.如图,把false经过一定的变换得到false,如果false上点false的坐标为false,那么这个点在false中的对应点false的坐标为( )
A.false B.false C.false D.false
2.将点P(-2,3)向右平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是( )
A.(-5,-3) B.(1,-3) C.(-1,-3) D.(5,-3)
3.如图,点A的坐标(﹣1,2),点A关于y轴的对称点的坐标为( )
A.(1,2) B.(﹣1,﹣2) C.(1,﹣2) D.(2,﹣1)
4.若点A(1﹣m,2)与点B(﹣1,n)关于y轴对称,则m+n=( )
A.2 B.0 C.﹣2 D.﹣4
5.平面直角坐标系中,与点false关于y轴对称的点是( )
A.false B.false C.false D.false
6.点A(﹣3,2)关于x轴的对称点A′的坐标为( )
A.(3,2) B.(3,﹣2) C.(﹣3,2) D.(﹣3,﹣2)
7.将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,顺次连接这三个点,得到另一个三角形,下列选项正确的是( )
A. B. C. D.
8.阳阳和亮亮喜欢下棋,阳阳持有圆形棋子,亮亮持有方形棋子.如图,若棋盘正中间的方形棋子的位置用false表示,最右上角的方形棋子的位置用false表示,阳阳应把第八枚圆形棋子放在适当位置,使所有棋子组成轴对称图形.则第八枚圆形棋子放的位置是( )
A.false B.false C.false D.false
9.在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是( )
A.(3,2) B.(3,﹣2) C.(﹣3,2) D.(﹣3,﹣2)
10.一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形。例如:若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l翻折,得到第二个图形。若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是false( )
A. B. C. D.
11.如图,在小正三角形组成的网格中,已有false个小正三角形涂黑,还需涂黑false个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则false的最小值为( )
A.false B.false C.false D.false
12.如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画( )条线段.
A.1 B.2 C.3 D.4
13.已知在平面直角坐标系中,点A的坐标为(﹣3,4),下列说法正确的有( )个
①点A与点B(-3,﹣4)关于x轴对称
②点A与点C(3,﹣4)关于原点对称
③点A与点F(-4,3)关于第二象限的平分线对称
④点A与点C(4,-3)关于第一象限的平分线对称
A.1 B.2 C.3 D.4
14.点false关于false轴的对称点false坐标为( )
A.false B.false C.false D.false
15.点false经过某种图形变换后得到点false这种图形变换可以是( )
A.关于false轴对称 B.关于false轴对称
C.绕原点逆时针旋转false D.绕原点顺时针旋转false
16.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
A.3cm B.4cm C.5cm D.6cm
17.如图,等边false的顶点false,false,规定把false“先沿false轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边false的顶点false的坐标为( )
A.false B.false C.false D.false
18.在坐标平面上有一个轴对称图形,其中A(3,﹣false)和B(3,﹣false)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1) B.(﹣2,﹣false) C.(﹣false,﹣9) D.(﹣2,﹣1)
二、填空题
19.在平面直角坐标系中,点A (m, 2)与点B (3, n)关于x轴对称,则false__________.
20.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则false的值是_____.
21.已知P(1,-2),则点P关于false轴的对称点的坐标是_______.
22.小明从前面的镜子里看到后面墙上挂钟的时间为2:30,则实际时间是_______________.
23.在镜子中看到时钟显示的时间是,则实际时间是__________
24.如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有________种.
25.若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是_____
26.如图,在3×3正方形网格中,黑色部分的图形构成一个轴对称图形,若在其余网格中再涂黑一个小正方形,使黑色部分的图形仍然构成一个轴对称图形,则可涂黑的小正方形共有______.
27.如图,点false与点false关于直线false对称,则false______.
28.已知点P(2,3),点A与点P关于y轴对称,则点A的坐标是______.
29.若点P(2,4)与点B(1-y,2x)关于y轴对称,那么y的值为_____________.
30.已知点A(x,-4)与点B(3,y)关于x轴对称,那么x+y的值为____________.
31.已知false(a?1,5)和false(2,b?1)关于x轴对称,则false的值为 _________ .
32.点false关于false轴的对称点的坐标为______.
33.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出_____个格点三角形与△ABC成轴对称.
34.如图,在false中,点A的坐标为false,点B的坐标为false,点C的坐标为false,点D在第二象限,且false与false全等,点D的坐标是______.
三、解答题
35.如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在网格线的交点上,点B关于y轴的对称点的坐标为(2,0),点C关于x轴的对称点的坐标为(﹣1,﹣2).
(1)根据上述条件,在网格中建立平面直角坐标系xOy;
(2)画出△ABC分别关于y轴的对称图形△A1B1C1;
(3)写出点A关于x轴的对称点的坐标.
36.如图,已知false各顶点的坐标分别为false,false,false,直线false经过点false,并且与false轴平行,false与false关于直线false对称.
(1)画出false,并写出点false的坐标 .
(2)若点false是false内一点,点false是false内与点false对应的点,则点false坐标 .
37.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.
38.在平面直角坐标系false中,已知false,false,false三点的坐标.
(1)写出点false关于原点false的对称点false的坐标,点false关于false轴的对称点false的坐标,点false关于false轴的对称点false的坐标;
(2)求(1)中的false的面积.
39.在平面直角坐标系中,已知点A(x,y),点B(x﹣my,mx﹣y)(其中m为常数,且m≠0),则称B是点A的“m族衍生点”.例如:点A(1,2)的“3族衍生点”B的坐标为(1﹣3×2,3×1﹣2),即B(﹣5,1).
(1)点(2,0)的“2族衍生点”的坐标为 ;
(2)若点A的“3族衍生点”B的坐标是(﹣1,5),则点A的坐标为 ;
(3)若点A(x,0)(其中x≠0),点A的“m族衍生点“为点B,且AB=OA,求m的值;
(4)若点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,则点A的位置在 .
40.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,false的顶点都在格点上,点false的坐标false,点false,点false.
(1)false将沿false轴向上平移3个单位得到false,画出false,并写出false的坐标.
(2)画出false关于false轴对称的false.
41.如图,在平面直角坐标系xOy中,A(-3,4),B(-4,1),C(-1,1).
(1)在图中作出△ABC关于x轴的轴对称图形△A′B′C′;
(2)直接写出A,B关于y轴的对称点A″,B″的坐标.
42.如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
43.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点和(顶点为网格线的交点),以及过格点的直线.
(1)将向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形;
(2)画出关于直线对称的三角形;
(3)填空: .
44.如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________
45.在直角坐标系中,false的三个顶点都在边长为false的小正方形的格点上,关false于false轴的对称图形为false,以false与false组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
(1)观察以上图形并填写下列各点坐标:
false,false,false,false(false为正整数)
(2)若false是这组图形中的一个三角形,当false时,则false ,false
参考答案
1.B
【解析】先观察△ABC和△A′B′C′得到把△ABC向上平移2个单位,再关于y轴对称可得到△A′B′C′,然后把点P(x,y)向上平移2个单位,再关于y轴对称得到点的坐标为(-x,y+2),即为P′点的坐标.
【解答】解:∵把△ABC向上平移2个单位,再关于y轴对称可得到△A′B′C′,
∴点P(x,y)的对应点P′的坐标为(-x,y+2).
故选:B.
【点评】本题考查了坐标与图形变化,解决本题的关键是根据已知对应点找到各对应点之间的变化规律.
2.C
【解答】解:∵点P(-2,3)向右平移3个单位得到点false,∴false,
∵点false与点false关于原点对称,∴false
故选C.
3.A
【解答】分析:直接利用关于y轴对称点的性质分析得出答案.
详解:点A的坐标(﹣1,2),点A关于y轴的对称点的坐标为:(1,2).
故选A.
点睛:此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.A
【解析】根据关于y轴的对称点的坐标特点可得m、n的值,进而可得m+n的值.
【解答】∵点A(1﹣m,2)与点B(﹣1,n)关于y轴对称,
∴1﹣m=1,n=2,
解得:m=0,n=2,
∴m+n=2,
故选:A.
【点评】本题主要考查了关于y轴的对称点的坐标特点,关键是掌握关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变.
5.C
【解析】根据平面直角坐标系中任意一点P(x,y),关于y轴对称的点的坐标为(-x,y),所此可得出答案.
【解答】根据关于x轴、y轴对称的点的坐标的特点,
∴点(2,-3)关于y轴对称的点的坐标是(-2,-3).
故选:C.
【点评】本题主要考查了平面直角坐标系中关于y轴对称的点的坐标的特点,注意掌握任意一点P(x,y),关于x轴的对称点的坐标是(x,-y),关于y轴对称的点的坐标为(-x,y),比较简单.
6.D
【解析】直接利用关于x轴对称点的性质得出符合题意的答案.
【解答】解:点A(﹣3,2)关于x轴的对称点A′的坐标为:(﹣3,﹣2),
故选:D.
【点评】本题考查了关于x轴对称的点的坐标特征,关于x轴对称的点:横坐标不变,纵坐标互为相反数.
7.A
【解析】根据将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,可得出对应点关于y轴对称,进而得出答案.
【解答】解:∵将△ABC各顶点的横坐标都乘以﹣1,纵坐标不变,顺次连接这三个点,得到另一个三角形,
∴对应点的坐标关于y轴对称,只有选项A符合题意.
故选A.
【点评】此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标变化与坐标轴的关系是解题关键.
8.C
【解析】本题考查平面直角坐标系的应用,需要根据题干已给具体坐标确定坐标系的原点所在,同时需要按照轴对称图形要求求解本题.
【解答】根据坐标(1,0),(2,1)可确定平面直角坐标系原点位于图形中最左边的圆形棋子处,按照轴对称图形要求,第八枚棋子应该放于左下方方形棋子的右边一格,即坐标(1,-1)
故答案为:C.
【点评】本题考查坐标系方式较为新颖,需要熟练掌握平面直角坐标系的象限特点,采取逆向思维求解本题.
9.D
【解答】试题分析:点(3,﹣2)关于y轴对称的点的坐标是(﹣3,﹣2)故选D.
考点:关于x轴、y轴对称点的坐标.
10.A
【解析】
试题解析:第一个正六边形下面标的数字为4,先绕其中心顺时针旋转4格,
旋转后的图形是,关于直线false的对称图形是.
故选A.
11.C
【解析】由等边三角形有三条对称轴可得答案.
【解答】如图所示,n的最小值为3.
故选C.
【点评】本题考查了利用轴对称设计图案,解题的关键是掌握常见图形的性质和轴对称图形的性质.
12.D
【解析】由轴对称图形的性质画出满足条件的所有线段即可.
【解答】如图:画出的线段有CD、DE、FG、HI,共4条.
故选D.
【点评】本题主要考查轴对称图形的性质.
13.D
【解析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数;关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变;关于第2象限角平分线对称的点的坐标特点:横纵坐标变换位置且变为相反数;关于第1象限角平分线对称的点的坐标特点:横纵坐标变换位置.综合以上即可得答案.
【解答】∵点A的坐标为(﹣3,4),
∴点A关于x轴对称的点的坐标为(﹣3,﹣4),
点A关于原点对称的点的坐标为(3,-4),
点A关于第二象限的角平分线对称的点的坐标为(-4,3)
点A关于第一象限的角平分线对称的点的坐标为(4,-3)
∴①、②、③、④正确.
故选:D.
【点评】此题主要考查了关于x轴、y轴、第二象限的角平分线、第一象限的角平分线对称的点的坐标规律,关键是熟练掌握点的变化规律,不要混淆.
14.A
【解析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答.
【解答】点A(2,1)关于x轴的对称点是(2,-1).
故选:A.
【点评】此题考查关于x轴、y轴对称的点的坐标,解题的关键是掌握好对称点的坐标规律.
15.A
【解析】直接利用利用关于x轴对称点的性质得出答案.
【解答】∵点(4,3)经过某种图形变化后得到点B(4,-3),
∴这种图形变化可以是关于x轴对称.
故选:A.
【点评】此题主要考查了关于x轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
16.C
【解析】
试题分析:根据轴对称的性质可得PM=P1M,PN=P2N,然后求出△PMN的周长=P1P2.
解:∵P点关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2,
∵△PMN的周长是5cm,
∴P1P2=5cm.
故选C.
考点:轴对称的性质.
17.D
【解析】先求出点C坐标,第一次变换,根据轴对称判断出点C变换后在x轴下方然后求出点C纵坐标,再根据平移的距离求出点C变换后的横坐标,最后写出第一次变换后点C坐标,同理可以求出第二次变换后点C坐标,以此类推可求出第n次变化后点C坐标.
【解答】∵△ABC是等边三角形AB=3-1=2
∴点C到x轴的距离为1+false,横坐标为2
∴C(2,false)
由题意可得:第1次变换后点C的坐标变为(2-1,false),即(1,false),
第2次变换后点C的坐标变为(2-2,false),即(0,false)
第3次变换后点C的坐标变为(2-3,false),即(-1,false)
第n次变换后点C的坐标变为(2-n,false)(n为奇数)或(2-n,false)(n为偶数),
∴连续经过2019次变换后,等边false的顶点false的坐标为(-2017,false),
故选:D
【点评】本题考查了利用翻折变换和平移的特点求解点的坐标,在求解过程中找到规律是关键.
18.A
【解析】先利用点A和点B的坐标特征可判断图形的对称轴为直线y=-4,然后写出点C关于直线y=-4的对称点即可.
【解答】解:∵A(3,﹣false)和B(3,﹣false)是图形上的一对对称点,
∴点A与点B关于直线y=﹣4对称,
∴点C(﹣2,﹣9)关于直线y=﹣4的对称点的坐标为(﹣2,1).
故选:A.
【点评】本题考查了坐标与图形的变化,需要注意关于直线对称:关于直线x=m对称,则两点的纵坐标相同,横坐标和为2m;关于直线y=n对称,则两点的横坐标相同,纵坐标和为2n.
19.false
【解析】直接利用关于x轴对称的点的性质得出m,n的值,进而得出答案.
【解答】解:∵点A (m, 2)与点B (3, n)关于x轴对称,
∴m=3,n=-2,
∴false.
故答案为:false.
【点评】此题主要考查了关于x轴对称的点的特征,熟记特征是解题关键.
20.1
【解析】根据关于x轴对称的两点的横坐标相同,纵坐标互为相反数求得a、b的值即可求得答案.
【解答】解:在直角坐标系中,关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
∴false=1,
故答案为:1.
【点评】本题考查了关于x轴对称的点的坐标特征,熟练掌握关于坐标轴对称的点的坐标特征是解题的关键.
21.(1,2)
【解答】解:关于x轴对称的点的坐标特征是横坐标相同,纵坐标互为相反数,
从而点P(1,-2)关于x轴对称的点的坐标是(1,2)
故答案为:(1,2)
【点评】本题考查关于x轴对称的点的坐标特征.
22.9:30
【解析】利用镜面对称的性质求解.镜面对称的性质:在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.
【解答】解:false时,分针竖直向下,时针指2和3之间,根据对称性可得:与false时的指针指向成轴对称,故实际时间是false.
【点评】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
23.16:25:08.
【解答】试题分析:∵实际时间和镜子中的时间关于竖直的线成轴对称,∴实际时间是16:25:08,
故答案为16:25:08.
考点:镜面对称.
24.5 种
【解析】根据轴对称图形的性质分别得出即可.
【解答】如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形.选择一个正方形涂黑,使得3个涂黑的正方形组成轴对称图形,选择的位置有以下几种:1,3,7,6,5,选择的位置共有5处.
25.-3
【解析】
试题解析:∵点M(a,﹣1)与点N(2,b)关于y轴对称,
∴a=﹣2,b=﹣1,
∴a+b=(﹣2)+(﹣1)=﹣3.
故答案为﹣3.
26.4.
【解析】直接利用轴对称图形的性质分析得出答案.
【解答】如图所示:当在空白处1到4个数字位置涂黑时,使黑色部分的图形仍然构成一个轴对称图形.
故答案为:4.
【点评】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
27.-5
【解析】根据点false与点false关于直线false对称求得a,b的值,最后代入求解即可.
【解答】解:∵点false与点false关于直线false对称
∴a=-2,false,解得b=-3
∴a+b=-2+(-3)=-5
故答案为-5.
【点评】本题考查了关于y=-1对称点的性质,根据对称点的性质求得a、b的值是解答本题的关键.
28.(-2,3)
【解析】
点P(2,3),点A与点P关于y轴对称,则点A的坐标是(?2,3),
故答案为(?2,3).
29.3
【解析】点P关于y轴对称,根据轴对称特点可解.
【解答】∵点P(2,4)与点B(1-y,2x)关于y轴对称,那么点P和点B横坐标数值互为相反数.
∴false
∴false
故答案为:3.
【点评】本题考查了坐标与图形变化-轴对称,熟练掌握轴对称坐标特点是解题的关键.
30.7
【解析】关于x轴对称,x不变,y变号,根据这个知识即可.
【解答】解:点A(x,-4)与点B(3,y)关于选轴对称,
所以有y=4,
x=3,
即x+y=7;
考查了学生对点关于坐标轴对称问题认识:
关于y轴对称,y不变,x变号;
关于x轴对称,x不变,y变号.
31.-1
【解析】根据两点关于x轴对称的坐标的关系,得a﹣1=2,b﹣1=﹣5,求出a,b的值,进而即可求解.
【解答】∵false 和false 关于x轴对称,
∴false
解得:false ,
∴false.
故答案为:﹣1.
【点评】本题主要考查平面直角坐标系中,两点关于x轴对称坐标的关系,掌握两点关于x轴对称,横坐标相等,纵坐标互为相反数,是解题的关键.
32.false
【解析】关于y轴对称的点,纵坐标相同,横坐标互为相反数.
【解答】∵关于y轴对称的点,纵坐标相同,横坐标互为相反数
∴点false关于y轴的对称点的坐标为false.
故答案为:false
【点评】考核知识点:轴对称与点的坐标.理解轴对称和点的坐标关系是关键.
33.6
【解析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解.
【解答】如图,最多能画出6个格点三角形与△ABC成轴对称.
故答案为:6.
【点评】本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.
34.(-4,2)或(-4,3)
【解答】把点C向下平移1个单位得到点D(4,2),这时△ABD与△ABC全等,分别作点C,D关于y轴的对称点(-4,3)和(-4,2),所得到的△ABD与△ABC全等.
故答案为(-4,2)或(-4,3).
35.(1)详见解析;(2)详见解析;(3)(-4,-4).
【解析】(1)依据点B关于y轴的对称点坐标为(2,0),点C关于x轴的对称点坐标为(-1,-2),即可得到坐标轴的位置;
(2)依据轴对称的性质,即可得到△ABC分别关于y轴的对称图形△A1B1C1;
(3)依据关于x轴的对称点的横坐标相同,纵坐标互为相反数,即可得到点A关于x轴的对称点的坐标.
【解答】解:(1)如图所示,建立平面直角坐标系xOy.
(2)如图所示,△A1B1C1即为所求;
(3)A点关于x轴的对称点的横坐标相同,纵坐标互为相反数,所以点A(-4,4)关于x轴的对称点的坐标(-4,-4).
【点评】本题主要考查作图?轴对称变换,解题的关键是熟练掌握轴对称变换的定义和性质.
36.(1) (1,2) ; (2) false.
【解析】(1)根据轴对称的性质找到各点的对应点,然后顺次连接即可,画出图形即可直接写出坐标.
(2)根据轴对称的性质可以直接写出false.
【解答】(1)如图所示:
直接通过图形得到false(1,2)
(2) 由题意可得:由于false与false 关于x=-1 对称
所以false.
【点评】此题主要考查了轴对称作图的知识,注意掌握轴对称的性质,找准各点的对称点是关键.
37.(1)见解析;(2) 见解析.
【解析】(1)利用△ABC三边长度,画出以A1为顶点的三角形三边长度即可,利用图象平移,可得出△A1B1C1.
(2)利用点B关于直线AC的对称点D,得出D点坐标,根据勾股定理和逆定理可得出AD与AB的位置关系.
【解答】(1)如图:
(2)∵AB=false,AD=false,BD=false,
∴AB2+AD2=BD2.
∴△ABD是直角三角形.
∴AD可以看作由AB绕A点逆时针旋转90°得到的.
【点评】本题考查了作图(平移变换、轴对称变换),全等图形,旋转和轴对称的性质,勾股定理和逆定理,图形变换有两种,全等变换和相似变换,掌握每种变换的概念、性质是作图的基础,一般难度不大.
38.(1) A′的坐标为(1,?5), B′的坐标为(4,?2), C′的坐标为(1,0);(2)false.
【解析】(1)根据点关于原点对称、关于x轴的对称和关于y轴对称的点的坐标特征求解;
(2)利用三角形面积公式求解.
【解答】(1)点A关于原点O的对称点A′的坐标为(1,?5),点B关于x轴的对称点B′的坐标为(4,?2),点C关于y轴的对称点C′的坐标为(1,0).
(2)以A′C′为底边,B′D为高,可得:△A′B′C′的面积=false×5×3=false.
【点评】此题考查坐标与图形-对称轴变换,解题关键在于掌握运算公式.
39.(1)(2,4);(2)(2,1);(3)m=±1;(4)y轴上
【解析】(1)利用“m族衍生点”的定义可求解;
(2)设点A坐标为(x,y),利用“m族衍生点”的定义列出方程组,即可求解;
(3)先求出点A的“m族衍生点“为点B(x,mx),由AB=OA,可求解;
(4)先求出点A(x,y)的“m族衍生点”为(x﹣my,mx﹣y),点A(x,y)的“﹣m族衍生点”为(x+my,﹣mx﹣y),由轴对称的性质可求x=0,即可求解.
【解答】解:(1)点(2,0)的“2族衍生点”的坐标为(2﹣2×0,2×2﹣0),即(2,4),
故答案为(2,4);
(2)设点A坐标为(x,y),
由题意可得:false,
∴false,
∴点A坐标为(2,1);
(3)∵点A(x,0),
∴点A的“m族衍生点“为点B(x,mx),
∴AB=|mx|,
∵AB=OA,
∴|x|=|mx|,
∴m=±1;
(4)∵点A(x,y),
∴点A(x,y)的“m族衍生点”为(x﹣my,mx﹣y),点A(x,y)的“﹣m族衍生点”为(x+my,﹣mx﹣y),
∵点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,
∴false,
∴x=0,
∴点A在y轴上,
故答案为:y轴上.
【点评】本题主要考查新定义问题,平面直角坐标系中关于y轴对称的点的坐标特征,二元一次方程组的解法,准确根据题意解题是关键.
40.(1)作图见详解,B1的坐标为(﹣2,﹣1);(2)见详解
【解析】(1)直接利用平移的性质分别得出对应点位置进而得出答案;
(2)直接利用关于y轴对称点的性质得出对应点位置进而得出答案.
【解答】解:(1)如图,△A1B1C1为所作,点B1的坐标为(﹣2,﹣1);
(2)如图,△A2B2C2为所作.
【点评】此题主要考查了平移变换以及轴对称变换,正确得出对应点位置是解题关键.
41.(1)见解析;(2)A″(3,4),B″(4,1).
【解析】(1)正确找出对应点A′,B′,C′即可得出△ABC关于x轴的轴对称图形△A′B′C′;
(2)根据关于y轴对称的点,纵坐标不变,横坐标改变符号直接写出即可.
【解答】(1)如图所示;
(2)点A(﹣3,4)、B(﹣4,1)关于y轴的对称点A″、B″的坐标分别为:A″(3,4),B″(4,1).
【点评】本题考查轴对称图形的作法以及关于坐标轴对称的点的坐标特点,灵活应用关于坐标轴对称的点的性质是解题的关键.
42.(1)14cm;(2)36°.
【解析】(1)折叠时,对称轴为折痕DE,DE垂直平分线段AB,由垂直平分线的性质得DA=DB,再把△ACD的周长进行线段的转化即可;
(2)设∠CAD=x,则∠BAD=2x,根据(1)DA=DB,可证∠B=∠BAD=2x,在Rt△ABC中,利用互余关系求x,再求∠B.
【解答】(1)由折叠的性质可知,DE垂直平分线段AB,
根据垂直平分线的性质可得:DA=DB,
所以,DA+DC+AC=DB+DC+AC=BC+AC=14cm;
(2)设∠CAD=x,则∠BAD=2x,
∵DA=DB,
∴∠B=∠BAD=2x,
在Rt△ABC中,∠B+∠BAC=90°,
即:2x+2x+x=90°,x=18°,
∠B=2x=36°.
【点评】考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.
43.(1)见解析;(2)见解析;(3)45
【解答】试题分析:(1)画一个图形的平移后的图形;(2)画出已知图形关于某直线对称的图形;(3)构造直角三角形即可.
试题解析:(1)如图所示;(2)如图所示;(3)45
考点: 作已知图形按照一定规则平移后的图形,及关于某直线成轴对称的图形.
44.(1)20;(2)80°;(3)∠EPF= 180°-2∠O
【解析】(1)根据轴对称的性质可得EM=EP,FP=FN,进而推出MN=EM+EF+FN=EP+EF+FP=△PEF的周长即可;
(2)由(1)及等腰三角形的性质、四边形的内角和找出∠M+∠N与∠O、∠EPF与∠O的关系即可;
(3)由(2)可直接得到∠EPF= 180°-2∠O.
【解答】解:(1)∵点M、N分别是点P关于AO、BO所在直线的对称点.
∴OA垂直平分PM,OB垂直平分PN,
∴EM=EP,FP=FN,
∴MN=EM+EF+FN=EP+EF+FP=△PEF的周长,
又∵△PEF的周长为20,
∴MN=20 cm.
(2)由(1)知:EM=EP,FP=FN,
∴∠PEF=2∠M,∠PFE=2∠N,
∵∠PCE=∠PDF=90°,
∴在四边形OCPD中,∠CPD+∠O=180°,
又∵在△PMN中,∠MPN+∠M+∠N=180°,且∠CPD+∠O=180°,
∴∠M+∠N=∠O=50°.
∴在△PEF中,∠EPF +∠PEF+∠PFE=∠EPF +2∠M +2∠N =180°,
即∠EPF=180°-2∠M -2∠N =180°-2(∠M +∠N)= 180°-2∠O=80°.
(3)由(2)可直接得到∠EPF= 180°-2∠O.
故答案为:∠EPF= 180°-2∠O.
【点评】本题主要考查轴对称的性质、四边形的内角和、等腰三角形的性质等,准确掌握轴对称性质的核心进行推理计算是解题的关键.
45.(1)false;false;false;(2)false,false.
【解析】(1)结合图形,先写出false、false的坐标,然后结合图形可发现规律,false,false,false的横坐标依次多4,纵坐标没变从而可得false的坐标;
false找出图中A、B、C的角码变化规律,然后根据false可得m、k得到值.
【解答】解:(1)由图可得false,false,false,
由图可得false,false,false的纵坐标不变,横坐标多一个就多4,
false的坐标为false,即false,
故答案为2,2;6,2;false,2;
(2)因为false,所以当n为奇数时,
由图可得,false对应false,false对应false,false对应false,false对应false,
false对应false,故当false时,false;
false对应C,B3对应false,false对应false,false,
false对应false,故当false时,false,
故答案为1010,1009.
【点评】本题主要考查了轴对称与坐标的变化关系,解答此题的关键是弄清向右翻折只变横坐标,纵坐标不变.
