人教七上数学1.1 正数和负数课件(31张PPT)
文档属性
| 名称 | 人教七上数学1.1 正数和负数课件(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 11:32:27 | ||
图片预览









文档简介
(共31张PPT)
第一章
有理数
1.1
正数和负数
第一章
有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
正数和负数
0的意义
相反意义的量
课时导入
数的产生和发展离不开生活和生产的需要,哪位
同学知道这些图片介绍的是什么内容?
知识点
正数和负数
知1-讲
感悟新知
1
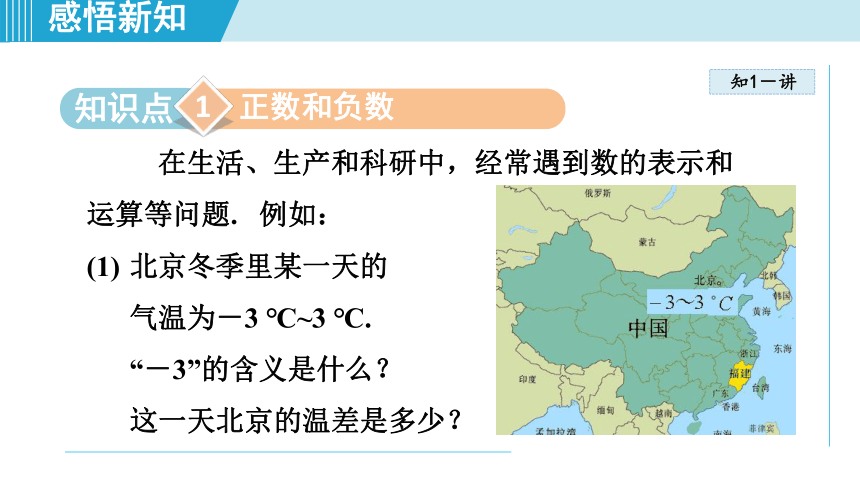
在生活、生产和科研中,经常遇到数的表示和
运算等问题.
例如:
北京冬季里某一天的
气温为-3
℃~3
℃.
“-3”的含义是什么?
这一天北京的温差是多少?
知1-讲
感悟新知
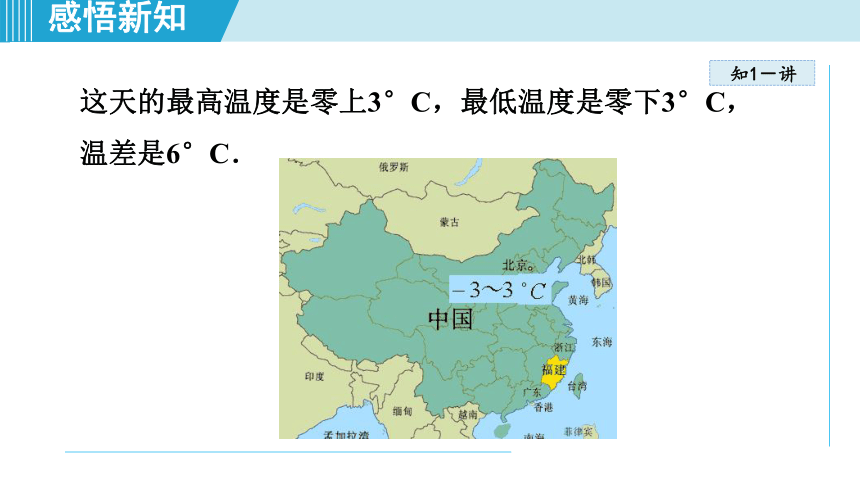
这天的最高温度是零上3°C,最低温度是零下3°C,
温差是6°C.
知1-讲
感悟新知
某年,我国花生产量比上一年增长1.8%,
油菜
籽产量比上一年增长-2.
7%.
“增长-2.
7%”
表
示什么意思?
知1-讲
感悟新知
这里,“结余-1.
2”是什么意思?怎么得到的?
日期
收入(+)或支出(-)
结余
注释
2日
3.5
8.5
卖废品
8日
-4.5
4.
0
买圆珠笔、铅笔芯
12日
-5.
2
-1.
2
买科普书,同学代付
收支情况表
夏新同学通过捡、卖废品,既保护了环境,
又积攒了
零花钱.下表是他某个月的部分收支情况
(单位:元).
知1-讲
感悟新知
上述几个问题这里出现了一种新数:
-3
表示零下3摄氏度,
-2.7%表示降低2.7%
,
-1.2表示亏空1.2
3
表示零上3摄氏度,
1.8%
表示增长1.8%
.
知1-讲
感悟新知
像3
、1.8%、3.5这样大于0的数叫做正数.
像-3,
-2.7%,-1.2,-4.5
,
…这样在正
数前加上符号“-”(负)的数叫做负数.
知1-讲
感悟新知
要点精析:
(1)正数的实质就是大于0的任何数,它可以含
“+”
(正)号,也可以不含“+”号;
(2)负数就是在正数前面加上“-”号;
(3)正数与负数的特征:
①不为零;
②含“+”、“-”号
(若既无“+”号也无“-”
号,等同于含“+”号)
.
感悟新知
知1-练
例
1
下列各数中,哪些是正数?哪些是负数?
+0.005,-100,
,-
,0.333…,-4,
5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
知1-讲
归
纳
感悟新知
判断正数、负数的方法:判断一个数是正数还
是负数,首先要确定它不为零;其次看它的“+”
“-”号的呈现形式:若不含“+”、“-”号,或
只含“+”号,或“-”号的个数为偶数,则均为
正数,否则为负数.
知2-练
感悟新知
例2
把下列各数填入表示相应集合的大括号内:
-3,+8
848,0,-
,2
016,-8.9,
-155,
.
导引:非正数指的是负数和零,非负数指的是正数
和零.
知1-讲
归
纳
感悟新知
1.非正数和非负数是两个常见的数学概念,非正数表
示0和负数,非负数表示0和正数;
2.集合中的3个点是省略号,表示集合中分别有无数
个正数和负数,填进去的只是其中的有限部分.
3.如果集合中没有省略号,那么我们在填入数后,必
须补上省略号.
感悟新知
知1-练
1
读下列各数,并指出其中哪些是正数,哪些是负数.
-1,2.5,+
,0,
-3.
14,120,
-1.732,-
解:正数:2.5,
,120
负数:-1,-3.14,-1.732,-
知识点
0的意义
知2-讲
感悟新知
2
想一想:
0是正数么?是负数么?
答:0既不是正数,也不是负数.
知2-讲
感悟新知
0是正数、负数的分界.
0的意义已经不仅表示“没有”.
比如:0摄氏度是一个确定的温度.
你能再举出一些用正数、负数、0表示数量
的例子么?
下列结论正确的是( )
A.不大于0的数一定是负数
B.海拔高度是0米表示没有高度
C.0是正数与负数的分界
D.不是正数的数一定是负数
导引:选项A中“不大于0”
表示的是:
“小于或等于0”;
选项B中“海拔高度是0米”表示的是:
“与海平
面一样高”;选项D中“不是正数的数”可以是负数或0.
感悟新知
知2-练
例
3
C
知2-讲
总
结
感悟新知
(1)
解选择题时,当正确选项无法确认时,可采用排
除法求解.如本例我们采用了排除法进行解答:
排除选项A、B、D后选择C.
(2)
“不大于”表示“小于或等于”,“不小于”表示
“大于或等于”.
感悟新知
知2-练
在-3,-5,-1,0四个数中,与其余三个数不同的
是( )
A.-3
B.-5
C.-1
D.0
D
知识点
相反意义的量
知3-讲
感悟新知
3
1.定义:在生活中存在各种各样的量,其中有一种量,
它们的属性相同(即同类量),但表示的意义却相反,
我们把这样的量叫做相反意义的量.
2.表示法:为了表示具有相反意义的量,我们把其中一
种意义的量规定为正,把另一种与之意义相反的量规
定为负.
知3-讲
感悟新知
特别解读
用正数、负数表示具有相反意义的量,在描述向指定方向变化的情况时,一般地,向指定方向变化用正数表示,
向指定方向的相反方向变化用负数表示.
(1)
一个月内,小明体重增加2
kg,小
华体重减少1kg,
小强体重无变化,写出他们这个月的体重增长值;
(2)某年,下列国家的商品进出口总额比上
年
的变化情况是:
美国减少6.
4%,德国增长1.
3%,
法国减少2.
4%,英国减少3.
5%,
意大利增长0.2%,
中国增长7.
5%.
写出这些国家这一年商品进出口总
额的增长率.
感悟新知
知3-练
例4
知3-练
感悟新知
解:
(1)这个月小明体重增长2
kg,小华体重增长-
1
kg,
小强体重增长0
kg.
(2)六个国家这一年商品进出口总额的增长率是:
美国
-6.4%,
德国
1.3%,
法国
-2.
4%,英国
-3.
5%,
意大利
0.2%,
中国
7.5%.
知3-讲
总
结
感悟新知
如果一个问题中出现相反意义的量,我们可以用
正数和负数分别表示它们.
感悟新知
知3-练
例5
找出下列各组相反意义的量:
①向南走6米;②进球5个;③高于海平面960米;
④盈利1
000元;⑤运进590吨粮食;⑥失球2个;
⑦亏损500元;⑧运出200吨粮食;⑨向北走30米;
⑩低于海平面30米.
导引:理解“相反意义”是找已知量的相反意义量的突破口.
解:相反意义的量分别为:①与⑨;②与⑥;③与⑩;
④与⑦;⑤与⑧.
知3-讲
总
结
感悟新知
判断相反意义的量的方法:要紧扣相反意义的量
的“两要素”,先看它是否意义相反,再看它是否是
同类量,两者缺一不可.
感悟新知
知3-练
如果80
m表示向东走80
m,那么-60
m表示
_______________.
2
如果水位升高3
m时水位变化记作+
3
m
,那么水
位下
降3
m时水位变化记作______m,
水位不升
不降时水位
变化记作______m.
向西走60米
-3
0
课堂小结
有理数
1.判断相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必
须是同类量.
(2)单位一致:两个具有相反意义的量在数量上可以
不相等,但单位必须一致.
课堂小结
有理数
2.正数、负数的定义:我们把以前学过的0以外的
数叫做正数,在这些数的前面带有“-”时叫
做负数.
根据需要有时在正数前面也加上“+”
(正号)表示正数.
3.
数0既不是正数,也不是负数,0是正数和负数
的分界.
必做:
请完成教材课后习题
课后作业
作业
第一章
有理数
1.1
正数和负数
第一章
有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
正数和负数
0的意义
相反意义的量
课时导入
数的产生和发展离不开生活和生产的需要,哪位
同学知道这些图片介绍的是什么内容?
知识点
正数和负数
知1-讲
感悟新知
1
在生活、生产和科研中,经常遇到数的表示和
运算等问题.
例如:
北京冬季里某一天的
气温为-3
℃~3
℃.
“-3”的含义是什么?
这一天北京的温差是多少?
知1-讲
感悟新知
这天的最高温度是零上3°C,最低温度是零下3°C,
温差是6°C.
知1-讲
感悟新知
某年,我国花生产量比上一年增长1.8%,
油菜
籽产量比上一年增长-2.
7%.
“增长-2.
7%”
表
示什么意思?
知1-讲
感悟新知
这里,“结余-1.
2”是什么意思?怎么得到的?
日期
收入(+)或支出(-)
结余
注释
2日
3.5
8.5
卖废品
8日
-4.5
4.
0
买圆珠笔、铅笔芯
12日
-5.
2
-1.
2
买科普书,同学代付
收支情况表
夏新同学通过捡、卖废品,既保护了环境,
又积攒了
零花钱.下表是他某个月的部分收支情况
(单位:元).
知1-讲
感悟新知
上述几个问题这里出现了一种新数:
-3
表示零下3摄氏度,
-2.7%表示降低2.7%
,
-1.2表示亏空1.2
3
表示零上3摄氏度,
1.8%
表示增长1.8%
.
知1-讲
感悟新知
像3
、1.8%、3.5这样大于0的数叫做正数.
像-3,
-2.7%,-1.2,-4.5
,
…这样在正
数前加上符号“-”(负)的数叫做负数.
知1-讲
感悟新知
要点精析:
(1)正数的实质就是大于0的任何数,它可以含
“+”
(正)号,也可以不含“+”号;
(2)负数就是在正数前面加上“-”号;
(3)正数与负数的特征:
①不为零;
②含“+”、“-”号
(若既无“+”号也无“-”
号,等同于含“+”号)
.
感悟新知
知1-练
例
1
下列各数中,哪些是正数?哪些是负数?
+0.005,-100,
,-
,0.333…,-4,
5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
知1-讲
归
纳
感悟新知
判断正数、负数的方法:判断一个数是正数还
是负数,首先要确定它不为零;其次看它的“+”
“-”号的呈现形式:若不含“+”、“-”号,或
只含“+”号,或“-”号的个数为偶数,则均为
正数,否则为负数.
知2-练
感悟新知
例2
把下列各数填入表示相应集合的大括号内:
-3,+8
848,0,-
,2
016,-8.9,
-155,
.
导引:非正数指的是负数和零,非负数指的是正数
和零.
知1-讲
归
纳
感悟新知
1.非正数和非负数是两个常见的数学概念,非正数表
示0和负数,非负数表示0和正数;
2.集合中的3个点是省略号,表示集合中分别有无数
个正数和负数,填进去的只是其中的有限部分.
3.如果集合中没有省略号,那么我们在填入数后,必
须补上省略号.
感悟新知
知1-练
1
读下列各数,并指出其中哪些是正数,哪些是负数.
-1,2.5,+
,0,
-3.
14,120,
-1.732,-
解:正数:2.5,
,120
负数:-1,-3.14,-1.732,-
知识点
0的意义
知2-讲
感悟新知
2
想一想:
0是正数么?是负数么?
答:0既不是正数,也不是负数.
知2-讲
感悟新知
0是正数、负数的分界.
0的意义已经不仅表示“没有”.
比如:0摄氏度是一个确定的温度.
你能再举出一些用正数、负数、0表示数量
的例子么?
下列结论正确的是( )
A.不大于0的数一定是负数
B.海拔高度是0米表示没有高度
C.0是正数与负数的分界
D.不是正数的数一定是负数
导引:选项A中“不大于0”
表示的是:
“小于或等于0”;
选项B中“海拔高度是0米”表示的是:
“与海平
面一样高”;选项D中“不是正数的数”可以是负数或0.
感悟新知
知2-练
例
3
C
知2-讲
总
结
感悟新知
(1)
解选择题时,当正确选项无法确认时,可采用排
除法求解.如本例我们采用了排除法进行解答:
排除选项A、B、D后选择C.
(2)
“不大于”表示“小于或等于”,“不小于”表示
“大于或等于”.
感悟新知
知2-练
在-3,-5,-1,0四个数中,与其余三个数不同的
是( )
A.-3
B.-5
C.-1
D.0
D
知识点
相反意义的量
知3-讲
感悟新知
3
1.定义:在生活中存在各种各样的量,其中有一种量,
它们的属性相同(即同类量),但表示的意义却相反,
我们把这样的量叫做相反意义的量.
2.表示法:为了表示具有相反意义的量,我们把其中一
种意义的量规定为正,把另一种与之意义相反的量规
定为负.
知3-讲
感悟新知
特别解读
用正数、负数表示具有相反意义的量,在描述向指定方向变化的情况时,一般地,向指定方向变化用正数表示,
向指定方向的相反方向变化用负数表示.
(1)
一个月内,小明体重增加2
kg,小
华体重减少1kg,
小强体重无变化,写出他们这个月的体重增长值;
(2)某年,下列国家的商品进出口总额比上
年
的变化情况是:
美国减少6.
4%,德国增长1.
3%,
法国减少2.
4%,英国减少3.
5%,
意大利增长0.2%,
中国增长7.
5%.
写出这些国家这一年商品进出口总
额的增长率.
感悟新知
知3-练
例4
知3-练
感悟新知
解:
(1)这个月小明体重增长2
kg,小华体重增长-
1
kg,
小强体重增长0
kg.
(2)六个国家这一年商品进出口总额的增长率是:
美国
-6.4%,
德国
1.3%,
法国
-2.
4%,英国
-3.
5%,
意大利
0.2%,
中国
7.5%.
知3-讲
总
结
感悟新知
如果一个问题中出现相反意义的量,我们可以用
正数和负数分别表示它们.
感悟新知
知3-练
例5
找出下列各组相反意义的量:
①向南走6米;②进球5个;③高于海平面960米;
④盈利1
000元;⑤运进590吨粮食;⑥失球2个;
⑦亏损500元;⑧运出200吨粮食;⑨向北走30米;
⑩低于海平面30米.
导引:理解“相反意义”是找已知量的相反意义量的突破口.
解:相反意义的量分别为:①与⑨;②与⑥;③与⑩;
④与⑦;⑤与⑧.
知3-讲
总
结
感悟新知
判断相反意义的量的方法:要紧扣相反意义的量
的“两要素”,先看它是否意义相反,再看它是否是
同类量,两者缺一不可.
感悟新知
知3-练
如果80
m表示向东走80
m,那么-60
m表示
_______________.
2
如果水位升高3
m时水位变化记作+
3
m
,那么水
位下
降3
m时水位变化记作______m,
水位不升
不降时水位
变化记作______m.
向西走60米
-3
0
课堂小结
有理数
1.判断相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必
须是同类量.
(2)单位一致:两个具有相反意义的量在数量上可以
不相等,但单位必须一致.
课堂小结
有理数
2.正数、负数的定义:我们把以前学过的0以外的
数叫做正数,在这些数的前面带有“-”时叫
做负数.
根据需要有时在正数前面也加上“+”
(正号)表示正数.
3.
数0既不是正数,也不是负数,0是正数和负数
的分界.
必做:
请完成教材课后习题
课后作业
作业
