人教七上数学1.2.4绝对值——绝对值的定义及性质课件(26张)
文档属性
| 名称 | 人教七上数学1.2.4绝对值——绝对值的定义及性质课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
1.2
有理数
第4课时
绝对值——绝对值
的定义及性质
第一章
有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
绝对值的意义
绝对值的求法
绝对值的性质
课时导入
旧知回顾
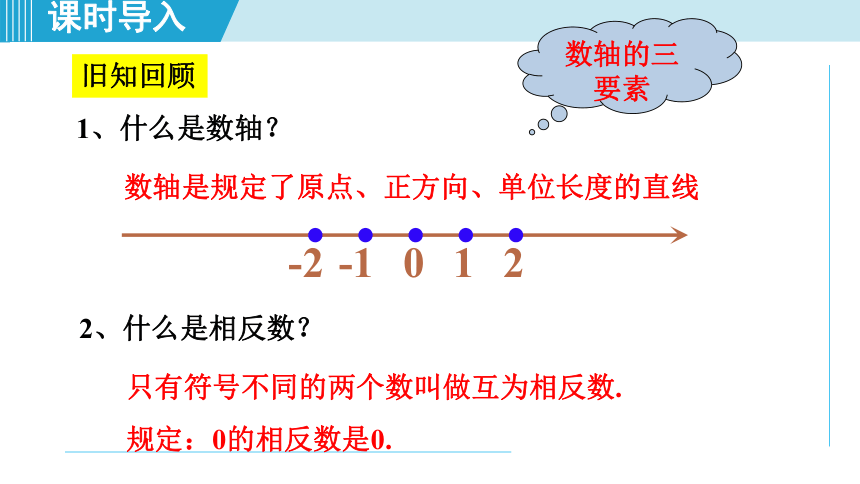
1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
0
1
2
-1
-2
2、什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
数轴的三要素
知识点
绝对值的意义
知1-讲
感悟新知
1
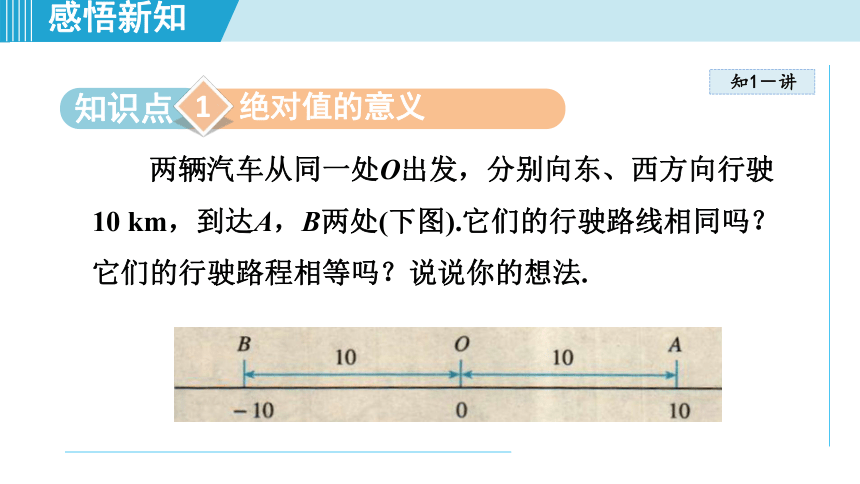
两辆汽车从同一处O出发,分别向东、西方向行驶
10
km,到达A,B两处(下图).它们的行驶路线相同吗?
它们的行驶路程相等吗?说说你的想法.
知1-讲
感悟新知
0
1
2
3
4
-1
-2
-3
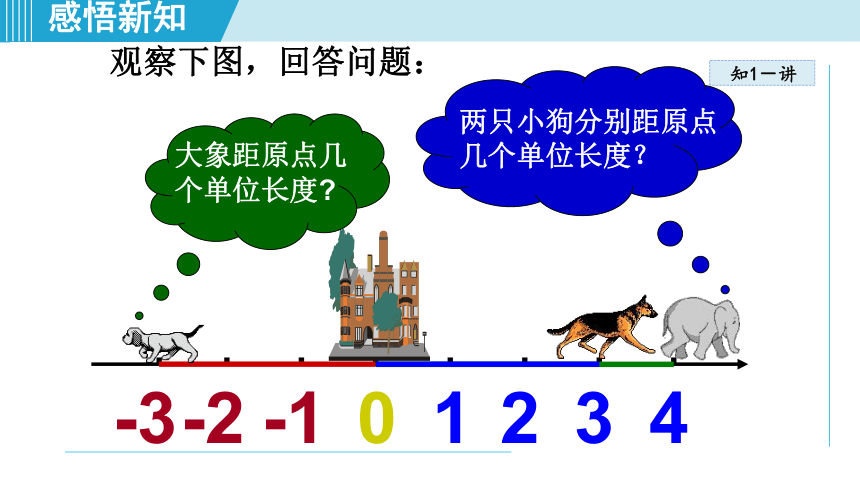
大象距原点几个单位长度?
两只小狗分别距原点几个单位长度?
观察下图,回答问题:
知1-讲
感悟新知
一般地,数轴上表示数a的点与原点的距离叫
做数a的绝对值,记作|a
|
.
(这里的数a可以是
正数、负数和0).
定义
由于绝对值是两点间的距离,所以绝对值不可能是负数.
知1-讲
感悟新知
特别提醒
由绝对值的定义可知:一个数对应的点离原点越近,它的绝对值越小,离原点越远,它的绝对值越大,所以没有绝对值最大的数,只有绝对值最小的数为0.
知1-练
感悟新知
1 (中考·连云港)数轴上表示-2的点与原点的距离是
________.
2
知识点
绝对值的求法
知2-讲
感悟新知
2
1.几何定义:一般地,数轴上表示数a的点与原点的距
离叫做数a的绝对值,记作
2.代数定义:一个正数的绝对值是它本身;一个负数
的绝对值是它的相反数;0的绝对值是0;任意一个
数的绝对值为唯一非负数.
用式子表示为:
知2-讲
感悟新知
特别提醒
绝对值的非负性是绝对值的一个重要性质,即对于任意有理数a,都有|
a
|
≥
0.
1.
当a
≠
0
时,|
a
|
>
0,当a=0
时,|
a
|=0.
2.
当|
a
|
>
0
时,a
≠
0,当|
a
|=0
时,a=0.
感悟新知
知2-练
例
1
导引:
写出下列各数的绝对值:
,0,
,
,-4.5,-5.
知2-练
感悟新知
知2-讲
总
结
感悟新知
求一个数的绝对值的方法:去掉绝对值符号时,必
须按照“先判后去”的原则,先判断这个数是正数、0或
负数,再根据绝对值的意义去掉绝对值符号,总之要确
保其结果为非负数且只有一个.
〈中考·镇江〉已知一个数的绝对值是4,则这
个数是________.
知2-练
感悟新知
例2
所以绝对值等于4的数有
±4
两个.
知2-讲
总
结
感悟新知
直接求一个数的绝对值是一个解;若已知一个数的
绝对值,反过来求这个数,则有两个解.即如果|x|=a
(a>0),则x=±a.
1 (中考·恩施州)-5的绝对值是( )
A.-5
B.-
C.
D.5
感悟新知
知2-练
D
2 (中考·东营)
的相反数是( )
A.
B.-
C.3
D.-3
B
知识点
绝对值的性质
知3-讲
感悟新知
3
想一想:
互为相反数的两个数的绝对值有什么关系?
0
-4
-3
-2
-1
3
2
1
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
感悟新知
知3-练
下列各式中无论m为何值,一定是正数的是
( )
A.
B.
C.
+1
D.-(-m)
不符合题意;选项D中-(-m)
C
=m显然不符合题意;选项C中,因为
例
3
感悟新知
知3-练
例4
已知
,求x与y的相反数.
知3-讲
总
结
感悟新知
本题运用了巧用非负性技巧,考查了非负数的性质,
该性质可巧记为“0+0=0”,可以推广为:如果几个非
负数的和为0,那么这几个非负数均为0.
知3-练
感悟新知
已知
,求a、b的值.
例
5
知3-讲
总
结
感悟新知
若几个非负数的和为0,则这几个数都为0.
感悟新知
知3-练
绝对值最小的数是________;绝对值最小的负整数
是________.
2
如果
+|b-1|=0,那么a+b=( )
A.
B.
C.
D.1
0
-1
C
3 写出下列各式的值,并回答问题.
知3-练
感悟新知
15
2.5
15
2.5
>
>
≥
课堂小结
有理数
(1)正数、负数的绝对值是正数;
(2)0的绝对值是0,0是绝对值最小的数;
(3)若一个数的绝对值是正数,则这样的数有两个,
它们互为相反数.
必做:
请完成教材课后习题
课后作业
作业
1.2
有理数
第4课时
绝对值——绝对值
的定义及性质
第一章
有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
绝对值的意义
绝对值的求法
绝对值的性质
课时导入
旧知回顾
1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
0
1
2
-1
-2
2、什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
数轴的三要素
知识点
绝对值的意义
知1-讲
感悟新知
1
两辆汽车从同一处O出发,分别向东、西方向行驶
10
km,到达A,B两处(下图).它们的行驶路线相同吗?
它们的行驶路程相等吗?说说你的想法.
知1-讲
感悟新知
0
1
2
3
4
-1
-2
-3
大象距原点几个单位长度?
两只小狗分别距原点几个单位长度?
观察下图,回答问题:
知1-讲
感悟新知
一般地,数轴上表示数a的点与原点的距离叫
做数a的绝对值,记作|a
|
.
(这里的数a可以是
正数、负数和0).
定义
由于绝对值是两点间的距离,所以绝对值不可能是负数.
知1-讲
感悟新知
特别提醒
由绝对值的定义可知:一个数对应的点离原点越近,它的绝对值越小,离原点越远,它的绝对值越大,所以没有绝对值最大的数,只有绝对值最小的数为0.
知1-练
感悟新知
1 (中考·连云港)数轴上表示-2的点与原点的距离是
________.
2
知识点
绝对值的求法
知2-讲
感悟新知
2
1.几何定义:一般地,数轴上表示数a的点与原点的距
离叫做数a的绝对值,记作
2.代数定义:一个正数的绝对值是它本身;一个负数
的绝对值是它的相反数;0的绝对值是0;任意一个
数的绝对值为唯一非负数.
用式子表示为:
知2-讲
感悟新知
特别提醒
绝对值的非负性是绝对值的一个重要性质,即对于任意有理数a,都有|
a
|
≥
0.
1.
当a
≠
0
时,|
a
|
>
0,当a=0
时,|
a
|=0.
2.
当|
a
|
>
0
时,a
≠
0,当|
a
|=0
时,a=0.
感悟新知
知2-练
例
1
导引:
写出下列各数的绝对值:
,0,
,
,-4.5,-5.
知2-练
感悟新知
知2-讲
总
结
感悟新知
求一个数的绝对值的方法:去掉绝对值符号时,必
须按照“先判后去”的原则,先判断这个数是正数、0或
负数,再根据绝对值的意义去掉绝对值符号,总之要确
保其结果为非负数且只有一个.
〈中考·镇江〉已知一个数的绝对值是4,则这
个数是________.
知2-练
感悟新知
例2
所以绝对值等于4的数有
±4
两个.
知2-讲
总
结
感悟新知
直接求一个数的绝对值是一个解;若已知一个数的
绝对值,反过来求这个数,则有两个解.即如果|x|=a
(a>0),则x=±a.
1 (中考·恩施州)-5的绝对值是( )
A.-5
B.-
C.
D.5
感悟新知
知2-练
D
2 (中考·东营)
的相反数是( )
A.
B.-
C.3
D.-3
B
知识点
绝对值的性质
知3-讲
感悟新知
3
想一想:
互为相反数的两个数的绝对值有什么关系?
0
-4
-3
-2
-1
3
2
1
原点
-3到原点的距离是3
+3到原点的距离是3
互为相反数的两个数的绝对值相等.
感悟新知
知3-练
下列各式中无论m为何值,一定是正数的是
( )
A.
B.
C.
+1
D.-(-m)
不符合题意;选项D中-(-m)
C
=m显然不符合题意;选项C中,因为
例
3
感悟新知
知3-练
例4
已知
,求x与y的相反数.
知3-讲
总
结
感悟新知
本题运用了巧用非负性技巧,考查了非负数的性质,
该性质可巧记为“0+0=0”,可以推广为:如果几个非
负数的和为0,那么这几个非负数均为0.
知3-练
感悟新知
已知
,求a、b的值.
例
5
知3-讲
总
结
感悟新知
若几个非负数的和为0,则这几个数都为0.
感悟新知
知3-练
绝对值最小的数是________;绝对值最小的负整数
是________.
2
如果
+|b-1|=0,那么a+b=( )
A.
B.
C.
D.1
0
-1
C
3 写出下列各式的值,并回答问题.
知3-练
感悟新知
15
2.5
15
2.5
>
>
≥
课堂小结
有理数
(1)正数、负数的绝对值是正数;
(2)0的绝对值是0,0是绝对值最小的数;
(3)若一个数的绝对值是正数,则这样的数有两个,
它们互为相反数.
必做:
请完成教材课后习题
课后作业
作业
