11.3如何提高机械效率习题 2021-2022学年沪粤版物理九年级上册(含答案)
文档属性
| 名称 | 11.3如何提高机械效率习题 2021-2022学年沪粤版物理九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 345.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览



文档简介
沪粤版九年级第十一章11.3如何提高机械效率习题精练
一、单选题
如图所示,若用瓶起子起瓶盖的机械效率为90%,这表示(????)
A. 若作用在瓶起子上的动力是10?N,则阻力是9?N
B. 若作用在瓶起子上的阻力是10?N,则动力是9?N
C. 若作用在瓶起子上的动力做功1?J,则有0.9?J的功用于起瓶盖
D. 若作用在瓶起子上的动力做功1?J,则有0.1?J的功用于起瓶盖
如图,为了提升重物,我们选用了粗细均匀、重为G的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在A、B两处,每次让杠杆上升同样的高度,下列说法正确的是? (??? )
A. 重物在A点处做的有用功多,杠杆的机械效率高
B. 重物在A点和B点处杠杆的机械效率相等
C. 重物在B点处做的有用功多,杠杆的机械效率高
D. 重物在B点处做的额外功多,杠杆的机械效率高
甲同学用水桶从井中提水;乙同学用绳把掉入井中的水桶捞上来,且水桶里有水。关于两位同学做有用功、额外功的说法中正确的是(????)
A. 甲同学提水桶过程中,克服水桶重力所做的功为有用功
B. 乙同学捞桶过程中,克服桶内水的重力所做的功为有用功
C. 甲同学提水桶过程中,克服桶内水的重力所做的功为有用功
D. 乙同学捞桶过程中,克服水桶重力所做的功为额外功
斜面的高与长如图所示,将重为200?N的物体沿斜面由底端匀速拉到斜面顶端,拉力为50?N,则下列说法正确的是(????)
A. 拉力做功200?J B. 额外功是200?J
C. 有用功是200?J D. 重力没有做功
如图,用滑轮或滑轮组提起同一重物,其中机械效率最高的是(????)
A. B. C. D.
如图所示的滑轮组,每个滑轮重20N,拉动绳子自由端,用这个滑轮组把重为380N的物体匀速提升3m,不计绳重和摩擦,g取10N/kg。下列选项正确的是(????)
A. 作用在绳自由端的拉力大小为400N
B. 该过程做的有用功为1200J
C. 该过程的机械效率为95%
D. 动滑轮越重,该滑轮组机械效率越大
工人用图示的滑轮组,在10?s内将300?N的重物匀速提升,绳子自由端移动的距离为6?m,滑轮组的机械效率是80%。下列说法正确的是(????)
A. 拉力F=100?N
B. 拉力对滑轮组做的功是600?J
C. 动滑轮的重力是75?N
D. 拉力F的功率为75?W
有一斜面长为L,高为h,现用力F沿斜面把重为G的物体从底端匀速拉到顶端.已知物体受到斜面的摩擦力为f,则下列关于斜面机械效率η的表达式正确的是(????)
A. η=G?fL×100% B. η=G?(F?f)L×100%
C. η=G?(F+f)L×100% D. η=G?G?+fL×100%
如图,在测定动滑轮机械效率的实验中,下列要求错误的是(????)
A. 弹簧测力计必须先校零
B. 弹簧测力计必须竖直向上拉
C. 弹簧测力计必须在静止时读数
D. 实验时装置旁的直尺必须竖直放置
如图所示,在探究“斜面的机械效率”的实验中,以下说法错误的是(? ? )
A. 用弹簧测力计沿斜面向上拉木块时,应尽量匀速
B. 斜面的倾斜程度影响斜面的机械效率
C. 斜面的倾斜程度越大,斜面机械效率越低
D. 斜面的倾斜程度越小,沿斜面所用的拉力越小
二、填空题
研究表明:省力的机械一定费距离,省距离的机械一定费力,既省力又省距离的机械是不存在的,也就是说使用任何机械都不能______,这就是______原理。
起重机将重6000?N的建材匀速提升了3?m,电动机做的功是3.6×104J,则起重机的机械效率是??????????;若只增加被提升的建材的重力,则起重机的效率??????????(填“变大”“变小”或“不变”)。
用图甲、乙两种方式匀速将重为100N的物体提升相同的高度,已知滑轮重20N,绳重和摩擦力不计。则手的拉力:F甲______F乙;拉力F对重物做的功W甲______W乙,机械效率:η甲______η乙(选填大于、小于或等于)。
如图是人抬起独轮车车把时的简化示意图,此时独轮车相当于一个??????????(填“省力”“费力”或“等臂”)杠杆;若该杠杆的动力臂是阻力臂的3倍,物体和车总重G=1200?N,抬起车把的力F=500?N,则此杠杆的机械效率为??????????。
三、实验探究题
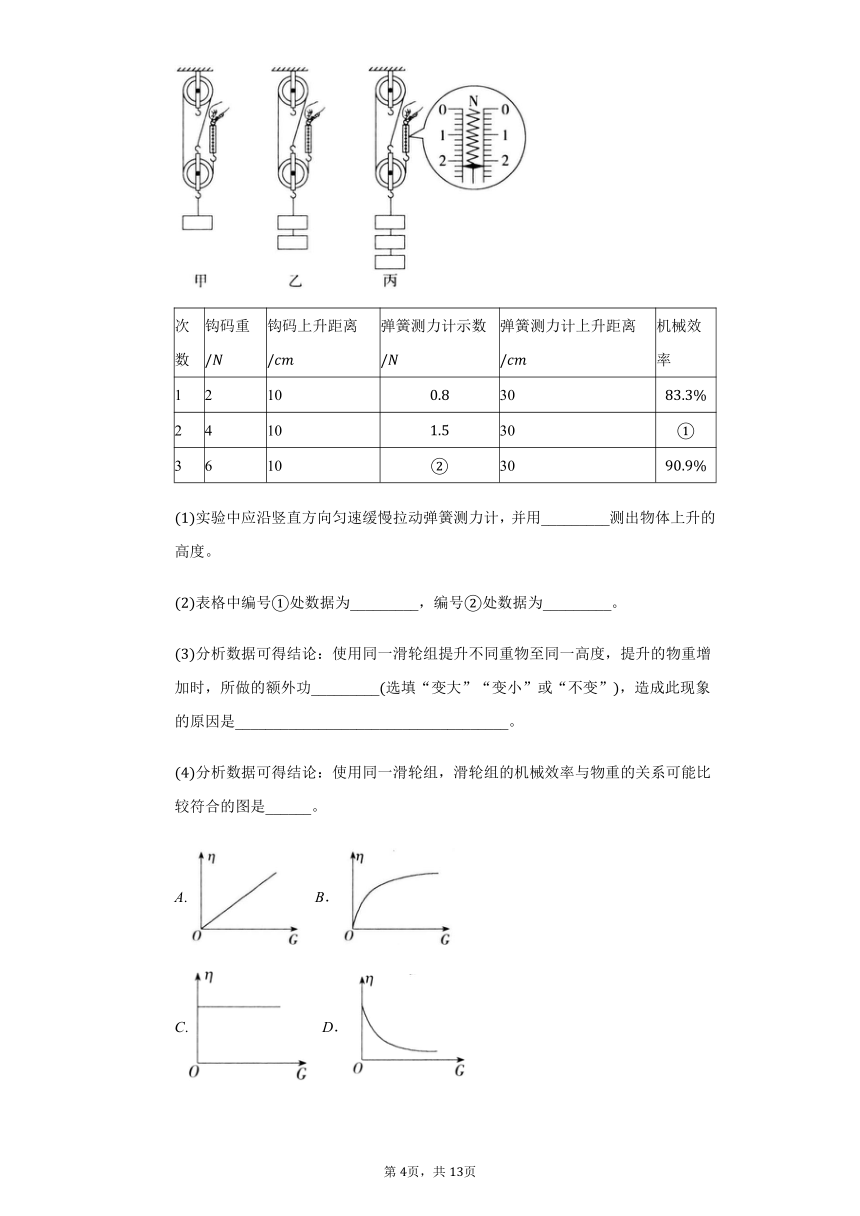
在“测量滑轮组机械效率”的实验中,小兵与同学们用同一滑轮组进行了三次实验(如图所示),实验数据记录如表。
次数
钩码重/N
钩码上升距离/cm
弹簧测力计示数/N
弹簧测力计上升距离/cm
机械效率
1
2
10
0.8
30
83.3%
2
4
10
1.5
30
①
3
6
10
②
30
90.9%
(1)实验中应沿竖直方向匀速缓慢拉动弹簧测力计,并用_________测出物体上升的高度。
(2)表格中编号①处数据为_________,编号②处数据为_________。
(3)分析数据可得结论:使用同一滑轮组提升不同重物至同一高度,提升的物重增加时,所做的额外功_________(选填“变大”“变小”或“不变”),造成此现象的原因是____________________________________。
(4)分析数据可得结论:使用同一滑轮组,滑轮组的机械效率与物重的关系可能比较符合的图是______。
A.? B.
C.? D.
(5)若将此滑轮组换一种绕绳方法,不计绳重及摩擦,提升相同的物体时,滑轮组的机械效率_________(选填“变大”“变小”或“不变”)。
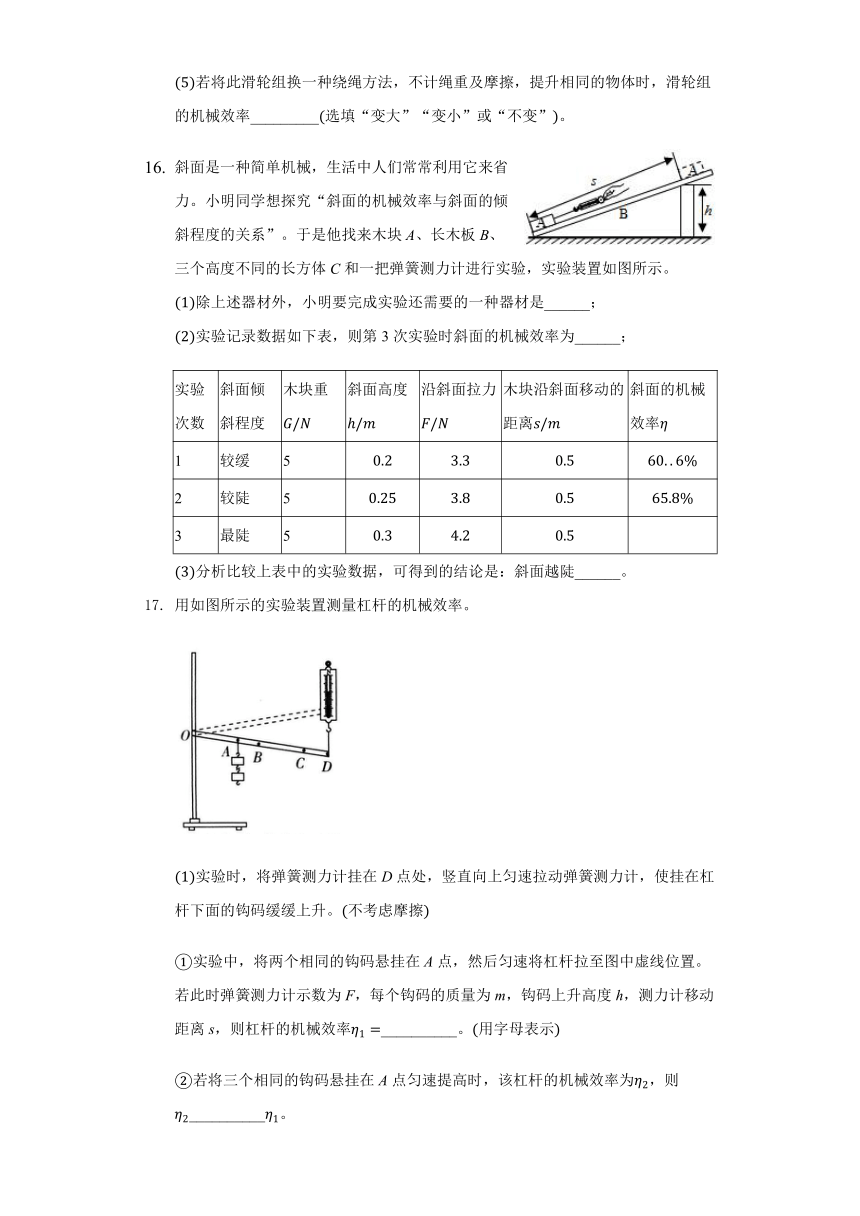
斜面是一种简单机械,生活中人们常常利用它来省力。小明同学想探究“斜面的机械效率与斜面的倾斜程度的关系”。于是他找来木块A、长木板B、三个高度不同的长方体C和一把弹簧测力计进行实验,实验装置如图所示。
(1)除上述器材外,小明要完成实验还需要的一种器材是______;
(2)实验记录数据如下表,则第3次实验时斜面的机械效率为______;
实验次数
斜面倾斜程度
木块重G/N
斜面高度?/m
沿斜面拉力F/N
木块沿斜面移动的距离s/m
斜面的机械效率η
1
较缓
5
0.2
3.3
0.5
60..6%
2
较陡
5
0.25
3.8
0.5
65.8%
3
最陡
5
0.3
4.2
0.5
(3)分析比较上表中的实验数据,可得到的结论是:斜面越陡______。
用如图所示的实验装置测量杠杆的机械效率。
(1)实验时,将弹簧测力计挂在D点处,竖直向上匀速拉动弹簧测力计,使挂在杠杆下面的钩码缓缓上升。(不考虑摩擦)
①实验中,将两个相同的钩码悬挂在A点,然后匀速将杠杆拉至图中虚线位置。若此时弹簧测力计示数为F,每个钩码的质量为m,钩码上升高度h,测力计移动距离s,则杠杆的机械效率η1=__________。(用字母表示)
②若将三个相同的钩码悬挂在A点匀速提高时,该杠杆的机械效率为η2,则η2__________η1。
③将同一物体分别悬挂在A、B两点,匀速使物体提高相同高度时的机械效率分别为ηA和ηB,则ηA__________ηB。
(2)若将同一物体悬挂在A点,弹簧测力计分别挂在C点和D点时,竖直向上匀速使物体提高相同高度时的机械效率分别为ηC和ηD,则ηC__________ηD。(以上三空均填“<”“=”或“>”)
在日常生活和工农业生产中,提高机械效率有着重要的意义.提高机械效率,要从研究影响机械效率的因素出发,寻求办法.
(1)为了探究影响机械效率的因素,小明选取了大小相同的滑轮,利用图甲和图乙装置进行实验,并把数据整理记录在下表中.
①比较1和2两次实验发现:在所用滑轮组一定时,提升的钩码_______________,机械效率越高.
②比较__________两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关.
③第5次实验室利用了图_________的装置完成的,判断依据是______________________________.
(2)小明利用图丙装置实验发现:斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关.保持斜面倾斜程度不变,可以采用_______________________的方法减小摩擦,从而提高斜面的机械效率.
(3)实验表明:额外功越小,总功越接近有用功:进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都__________.下列物理规律的得出运用了这种研究方法的是(????)
A.焦耳定律???? B.牛顿第一定律????? C.阿基米德原理???? D.欧姆定律
答案和解析
1.【答案】C
【解析】解:瓶起子可看成是一个杠杆,根据杠杆的平衡条件F1L1=F2L2知,要比较动力和阻力做功的大小,必须知道动力臂和阻力臂的大小,故A、B错误;瓶起子的机械效率为90%,表示在起瓶盖过程中,在总功中有90%是用来起瓶盖的有用功,10%是额外功,即若动力做功1?J,则有0.9?J的功用于起瓶盖,故C正确,D错误。故选C。
2.【答案】C
【解析】解:利用杠杆提升重物,有用功W有用=G物?,在A、B两点处提升的是同一个重物,每次杠杆上升同样的高度,而重物上升的高度?B>?A,在A、B两处做的有用功不相同,重物在A点处做的有用功少,故A选项错误。
由图可知:在A、B两处提升重物,每次让杠杆上升同样的高度,而杠杆重心上升的高度?'A=?'B,额外功:W额外=G?,W额外A=W额外B,故D错误;
在A、B两处人对重物提升的高度不同,做的有用功不相同,W有用A故选C。
3.【答案】C
【解析】极:本题中,甲、乙两位同学都是从井中向上提水桶,但甲的目的是提水,乙的目的是捞桶。根据有用功和额外功的概念可知,甲同学提水桶过程中,克服桶内水的重力所做的功为有用功,克服桶的重力所做的功为额外功;乙同学在捞桶的过程中,克服水桶重力所做的功为有用功,克服桶内水的重力所做的功为额外功。
4.【答案】B
【解析】解:拉力做功W总=Fl=50?N×20?m=1000?J,故A错误;有用功W有用=G?=200?N×4?m=800?J,故C错误;额外功W额外=W总?W有用=1000?J?800?J=200?J,故B正确;重力的方向竖直向下,物体在竖直方向上移动了4?m,所以重力做了功,故D错误。故选B。
5.【答案】B
【解析】
机械效率的计算公式是η=W有W总,由“用滑轮或滑轮组提起同一重物”可知这几个装置的所做的有用功是相等的,η的高低就取决于W总;而W总=W有+W额外,使用滑轮或滑轮组时所做的额外功主要是克服动滑轮重和绳重、摩擦所做的功;
只有图B是一个定滑轮,在提升高度相等的条件下,额外功较少,总功也随之较少,有用功一定时,总功少,所以机械效率较高。故选B。
??6.【答案】C
【解析】解:
根据图示可知,n=2,拉力端移动的距离:s=2?=2×3m=6m;
A、不计绳重和摩擦,作用在绳子自由端的拉力:F=12(G+G动)=12×(380N+20N)=200N,故A错误;
B、拉力做的有用功:W有用=G?=380N×3m=1140J,故B错误;
C、总功:W总=Fs=200N×6m=1200J,
滑轮组的机械效率:
η=W有用W总=1140J1200J×100%=95%;故C正确;
D、不计绳重和摩擦,提升相同的物体,做相同有用功的情况下,动滑轮越重,额外功越大、总功越大,所以机械效率越低,故D错误。
故选:C。
7.【答案】D
【解析】解:由图知,n=3,绳子自由端移动的距离s=3?,滑轮组的机械效率η=W有用W总×100%=
G?Fs×100%=GnF×100%=g3F×100%,则拉力F=G3η=300N3×80%=125N,故A错误;拉力对滑轮组做的功:W总=Fs=125?N×6?m=750?J,故B错误;不计绳重和摩擦,拉力F=
13(G+G动),则动滑轮重力G动=3F?G=3×125?N?300?N=75?N,但实际上存在摩擦、绳重,则动滑轮的重力不是75?N,故C错误;拉力做功的功率:P=W总t=750J10s=75W,故D正确。
8.【答案】D
【解析】解:斜面高为h,物重为G,W有用=G?,又斜面长为L,拉力为F,W总=FL,则η=W有用W总×100%=G?FL×100%,而物体与斜面的摩擦力为f,W额外=fL,W总=W有用+W额外=G?+fL,η=W有用W总×100%=G?G?+fL×100%.
9.【答案】C
【解析】略
10.【答案】C
【解析】略
11.【答案】省功? 功的
【解析】解:有的机械可以省力,有的机械可以省距离,还有的机械还可以改变力的方向;但省力的机械必然费距离;省距离的机械一定费力;由功的原理可知,使用任何机械都不能省功,但使用机械有许多好处。
故答案为:省功;功的。
使用机械可以在省力、改变动力的方向或移动的距离上得到好处,给人们带来方便,做到方便快捷等;使用机械有这么多的好处,这正是人们使用机械的目的,但使用任何机械都不能省功。
12.【答案】50%
?变大
【解析】解:起重机克服建材重力做的功:W有用=G?=6000?N×3?m=1.8×104?J;起重机的机械效率:η=W有用W总×100%=1.8×104J3.6×104J×100%=50%;若只增加被提升的建材的重力,则有用功变大,额外功不变,根据η=W有用W总=W有用W有用+W额外=11+W额外W有用可知,起重机的机械效率会变大。
13.【答案】大于? 等于? 大于
【解析】解:绳重和摩擦力不计,由定滑轮的使用特点可知:F甲=G;
由动滑轮的使用特点可知:F乙=12(G动+G);
一般情况下,动滑轮重小于物重,因此F甲>F乙。
如图所示,用定滑轮和动滑轮分别将质量相同的甲、乙两物体匀速提升相同的高度,不计绳重与摩擦,则所做的有用功一样大,即拉力F对重物做的功W甲=W乙,
乙图,要克服动滑轮的重力做额外功,所以使用动滑轮做的总功多,由η=W有W总可知,动滑轮的机械效率低,即η甲>η乙。
故答案为:大于;等于;大于。
14.【答案】省力 80%
【解析】解:由独轮车的简化示意图可知,独轮车在使用时动力臂大于阻力臂,所以它属于省力杠杆;
由题可知L1:L2=s:?=3:1,
则杠杆的机械效率η=W有用W总×100%=G?Fs×100%=1200N×1500N×3×100%=80%。
15.【答案】(1)刻度尺;(2)88.9%;2.2;(3)变大;物重增加,轮和轴之间的压力变大,摩擦力变大?;(4)B?;(5)不变。
【解析】解:(1)实验时应沿竖直方向匀速缓慢拉动弹簧测力计,并用刻度尺测量出物体上升的高度;
(2)第2次实验的机械效率为η=W有用W总×100%=G?Fs×100%=4?N×0.1?m1.5?N×0.3?m×100%=88.9%,图丙中弹簧测力计分度值为0.2?N,示数为2.2?N,故编号②处数据为2.2;
(3)进一步分析数据,可知用同一滑轮组提升不同重物至同一高度,提升的物重增加时,所做的额外功将变大,因为物重增加,轮和轴之间的压力变大,摩擦力变大;
(4)动滑轮重力不可忽略,则克服动滑轮重和绳与滑轮、滑轮与轴间的摩擦所做的功为额外功,物重增大,有用功逐渐增大,有用功占总功的比值在增大,所以机械效率逐渐增大,但从摩擦角度考虑,随着物体重力的增加,滑轮与绳子间摩擦会有一定程度增大,故机械效率η与物体重力G的关系并不成正比,故B符合题意;
(5)不计绳重及摩擦,则克服动滑轮的自重做功为额外功的唯一来源,若将此滑轮组换一种绕绳方法,提升相同的物体时,滑轮组的机械效率η=W有用W总×100%=W有用W有用+W额外×100%=G物?(G物+G动)?×100%=G物G物+G动×100%,因G物和G动不变,故滑轮组的机械效率不变。
【答案】刻度尺? 71.4%? 机械效率越高
【解析】解:(1)要测量斜面的高度和木块沿斜面移动的距离就要使用长度的测量工具---刻度尺。
(2)第3次实验时,有用功W有=G?=5N×0.3m=1.5J,
总功W总=Fs=4.2N×0.5m=2.1J,
斜面的机械效率η=η=W有W总×100%=1.5J2.1J×100%≈71.4%。
(3)由图中数据可知:斜面的倾斜程度越大,斜面的机械效率越高
故答案为:(1)刻度尺;(2)71.4%;(3)机械效率越高。
17.【答案】(1)①2mg?Fs×100%?②>?③【解析】解:(1)①在实验过程中,有用功W有用=G?=2mg?,总功W总=Fs,所以杠杆的机械效率η=W有用W总×100%=2mg?Fs×100%。
②将三个相同的钩码悬挂在A点匀速提高时,所做的额外功相同,有用功增加,即有用功占总功的比例变大,所以此时杠杆的机械效率变大,即η2>η1。
③将同一物体由悬挂的A点变为B点时,阻力臂变大,由杠杆的平衡条件可知拉力F变大,杠杆提升的高度减小,额外功减小,因此有用功占总功的比例变大,杠杆的机械效率变大,即ηA<ηB。
(2)若将同一物体悬挂在A点,弹簧测力计分别挂在C点和D点时,竖直向上匀速使物体提高相同高度时,所做的有用功相同,额外功也相同,故总功相同,根据机械效率公式可知,机械效率相同,ηC=ηD。
18.【答案】(1)①越重;②2和3;③乙;绳子的有效段数为1;
(2)减小接触面的粗糙程度;
(3)不省功;B
【解析】
(1)①比较1和2两次实验发现:在所用滑轮组相同时,提升物体的重力越大,机械效率越高,即所用滑轮组一定时,提升的钩码重力越大,机械效率越高;
②比较2和3两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关;
③第5次实验室利用了图乙的装置完成的,判断依据是:n=s?=0.2m0.2m=1,即绳子的有效段数为1;
(2)保持斜面倾斜程度不变,可以采用减小接触面粗糙程度的方法减小摩擦,从而提高斜面的机械效率;
(3)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功,可见使用任何机械都不省功,采用了实验推理法,而焦耳定律、阿基米德原理、欧姆定律可通过实验直接验证,故ACD不合题意;牛顿第一定律不能用实验直接验证,是在实验的基础下推理得出的,故B符合题意。
故选B。
故答案为:(1)①越重;②2和3;③乙;绳子的有效段数为1;(2)减小接触面的粗糙程度;(3)不省功;B。
一、单选题
如图所示,若用瓶起子起瓶盖的机械效率为90%,这表示(????)
A. 若作用在瓶起子上的动力是10?N,则阻力是9?N
B. 若作用在瓶起子上的阻力是10?N,则动力是9?N
C. 若作用在瓶起子上的动力做功1?J,则有0.9?J的功用于起瓶盖
D. 若作用在瓶起子上的动力做功1?J,则有0.1?J的功用于起瓶盖
如图,为了提升重物,我们选用了粗细均匀、重为G的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在A、B两处,每次让杠杆上升同样的高度,下列说法正确的是? (??? )
A. 重物在A点处做的有用功多,杠杆的机械效率高
B. 重物在A点和B点处杠杆的机械效率相等
C. 重物在B点处做的有用功多,杠杆的机械效率高
D. 重物在B点处做的额外功多,杠杆的机械效率高
甲同学用水桶从井中提水;乙同学用绳把掉入井中的水桶捞上来,且水桶里有水。关于两位同学做有用功、额外功的说法中正确的是(????)
A. 甲同学提水桶过程中,克服水桶重力所做的功为有用功
B. 乙同学捞桶过程中,克服桶内水的重力所做的功为有用功
C. 甲同学提水桶过程中,克服桶内水的重力所做的功为有用功
D. 乙同学捞桶过程中,克服水桶重力所做的功为额外功
斜面的高与长如图所示,将重为200?N的物体沿斜面由底端匀速拉到斜面顶端,拉力为50?N,则下列说法正确的是(????)
A. 拉力做功200?J B. 额外功是200?J
C. 有用功是200?J D. 重力没有做功
如图,用滑轮或滑轮组提起同一重物,其中机械效率最高的是(????)
A. B. C. D.
如图所示的滑轮组,每个滑轮重20N,拉动绳子自由端,用这个滑轮组把重为380N的物体匀速提升3m,不计绳重和摩擦,g取10N/kg。下列选项正确的是(????)
A. 作用在绳自由端的拉力大小为400N
B. 该过程做的有用功为1200J
C. 该过程的机械效率为95%
D. 动滑轮越重,该滑轮组机械效率越大
工人用图示的滑轮组,在10?s内将300?N的重物匀速提升,绳子自由端移动的距离为6?m,滑轮组的机械效率是80%。下列说法正确的是(????)
A. 拉力F=100?N
B. 拉力对滑轮组做的功是600?J
C. 动滑轮的重力是75?N
D. 拉力F的功率为75?W
有一斜面长为L,高为h,现用力F沿斜面把重为G的物体从底端匀速拉到顶端.已知物体受到斜面的摩擦力为f,则下列关于斜面机械效率η的表达式正确的是(????)
A. η=G?fL×100% B. η=G?(F?f)L×100%
C. η=G?(F+f)L×100% D. η=G?G?+fL×100%
如图,在测定动滑轮机械效率的实验中,下列要求错误的是(????)
A. 弹簧测力计必须先校零
B. 弹簧测力计必须竖直向上拉
C. 弹簧测力计必须在静止时读数
D. 实验时装置旁的直尺必须竖直放置
如图所示,在探究“斜面的机械效率”的实验中,以下说法错误的是(? ? )
A. 用弹簧测力计沿斜面向上拉木块时,应尽量匀速
B. 斜面的倾斜程度影响斜面的机械效率
C. 斜面的倾斜程度越大,斜面机械效率越低
D. 斜面的倾斜程度越小,沿斜面所用的拉力越小
二、填空题
研究表明:省力的机械一定费距离,省距离的机械一定费力,既省力又省距离的机械是不存在的,也就是说使用任何机械都不能______,这就是______原理。
起重机将重6000?N的建材匀速提升了3?m,电动机做的功是3.6×104J,则起重机的机械效率是??????????;若只增加被提升的建材的重力,则起重机的效率??????????(填“变大”“变小”或“不变”)。
用图甲、乙两种方式匀速将重为100N的物体提升相同的高度,已知滑轮重20N,绳重和摩擦力不计。则手的拉力:F甲______F乙;拉力F对重物做的功W甲______W乙,机械效率:η甲______η乙(选填大于、小于或等于)。
如图是人抬起独轮车车把时的简化示意图,此时独轮车相当于一个??????????(填“省力”“费力”或“等臂”)杠杆;若该杠杆的动力臂是阻力臂的3倍,物体和车总重G=1200?N,抬起车把的力F=500?N,则此杠杆的机械效率为??????????。
三、实验探究题
在“测量滑轮组机械效率”的实验中,小兵与同学们用同一滑轮组进行了三次实验(如图所示),实验数据记录如表。
次数
钩码重/N
钩码上升距离/cm
弹簧测力计示数/N
弹簧测力计上升距离/cm
机械效率
1
2
10
0.8
30
83.3%
2
4
10
1.5
30
①
3
6
10
②
30
90.9%
(1)实验中应沿竖直方向匀速缓慢拉动弹簧测力计,并用_________测出物体上升的高度。
(2)表格中编号①处数据为_________,编号②处数据为_________。
(3)分析数据可得结论:使用同一滑轮组提升不同重物至同一高度,提升的物重增加时,所做的额外功_________(选填“变大”“变小”或“不变”),造成此现象的原因是____________________________________。
(4)分析数据可得结论:使用同一滑轮组,滑轮组的机械效率与物重的关系可能比较符合的图是______。
A.? B.
C.? D.
(5)若将此滑轮组换一种绕绳方法,不计绳重及摩擦,提升相同的物体时,滑轮组的机械效率_________(选填“变大”“变小”或“不变”)。
斜面是一种简单机械,生活中人们常常利用它来省力。小明同学想探究“斜面的机械效率与斜面的倾斜程度的关系”。于是他找来木块A、长木板B、三个高度不同的长方体C和一把弹簧测力计进行实验,实验装置如图所示。
(1)除上述器材外,小明要完成实验还需要的一种器材是______;
(2)实验记录数据如下表,则第3次实验时斜面的机械效率为______;
实验次数
斜面倾斜程度
木块重G/N
斜面高度?/m
沿斜面拉力F/N
木块沿斜面移动的距离s/m
斜面的机械效率η
1
较缓
5
0.2
3.3
0.5
60..6%
2
较陡
5
0.25
3.8
0.5
65.8%
3
最陡
5
0.3
4.2
0.5
(3)分析比较上表中的实验数据,可得到的结论是:斜面越陡______。
用如图所示的实验装置测量杠杆的机械效率。
(1)实验时,将弹簧测力计挂在D点处,竖直向上匀速拉动弹簧测力计,使挂在杠杆下面的钩码缓缓上升。(不考虑摩擦)
①实验中,将两个相同的钩码悬挂在A点,然后匀速将杠杆拉至图中虚线位置。若此时弹簧测力计示数为F,每个钩码的质量为m,钩码上升高度h,测力计移动距离s,则杠杆的机械效率η1=__________。(用字母表示)
②若将三个相同的钩码悬挂在A点匀速提高时,该杠杆的机械效率为η2,则η2__________η1。
③将同一物体分别悬挂在A、B两点,匀速使物体提高相同高度时的机械效率分别为ηA和ηB,则ηA__________ηB。
(2)若将同一物体悬挂在A点,弹簧测力计分别挂在C点和D点时,竖直向上匀速使物体提高相同高度时的机械效率分别为ηC和ηD,则ηC__________ηD。(以上三空均填“<”“=”或“>”)
在日常生活和工农业生产中,提高机械效率有着重要的意义.提高机械效率,要从研究影响机械效率的因素出发,寻求办法.
(1)为了探究影响机械效率的因素,小明选取了大小相同的滑轮,利用图甲和图乙装置进行实验,并把数据整理记录在下表中.
①比较1和2两次实验发现:在所用滑轮组一定时,提升的钩码_______________,机械效率越高.
②比较__________两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关.
③第5次实验室利用了图_________的装置完成的,判断依据是______________________________.
(2)小明利用图丙装置实验发现:斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关.保持斜面倾斜程度不变,可以采用_______________________的方法减小摩擦,从而提高斜面的机械效率.
(3)实验表明:额外功越小,总功越接近有用功:进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都__________.下列物理规律的得出运用了这种研究方法的是(????)
A.焦耳定律???? B.牛顿第一定律????? C.阿基米德原理???? D.欧姆定律
答案和解析
1.【答案】C
【解析】解:瓶起子可看成是一个杠杆,根据杠杆的平衡条件F1L1=F2L2知,要比较动力和阻力做功的大小,必须知道动力臂和阻力臂的大小,故A、B错误;瓶起子的机械效率为90%,表示在起瓶盖过程中,在总功中有90%是用来起瓶盖的有用功,10%是额外功,即若动力做功1?J,则有0.9?J的功用于起瓶盖,故C正确,D错误。故选C。
2.【答案】C
【解析】解:利用杠杆提升重物,有用功W有用=G物?,在A、B两点处提升的是同一个重物,每次杠杆上升同样的高度,而重物上升的高度?B>?A,在A、B两处做的有用功不相同,重物在A点处做的有用功少,故A选项错误。
由图可知:在A、B两处提升重物,每次让杠杆上升同样的高度,而杠杆重心上升的高度?'A=?'B,额外功:W额外=G?,W额外A=W额外B,故D错误;
在A、B两处人对重物提升的高度不同,做的有用功不相同,W有用A
3.【答案】C
【解析】极:本题中,甲、乙两位同学都是从井中向上提水桶,但甲的目的是提水,乙的目的是捞桶。根据有用功和额外功的概念可知,甲同学提水桶过程中,克服桶内水的重力所做的功为有用功,克服桶的重力所做的功为额外功;乙同学在捞桶的过程中,克服水桶重力所做的功为有用功,克服桶内水的重力所做的功为额外功。
4.【答案】B
【解析】解:拉力做功W总=Fl=50?N×20?m=1000?J,故A错误;有用功W有用=G?=200?N×4?m=800?J,故C错误;额外功W额外=W总?W有用=1000?J?800?J=200?J,故B正确;重力的方向竖直向下,物体在竖直方向上移动了4?m,所以重力做了功,故D错误。故选B。
5.【答案】B
【解析】
机械效率的计算公式是η=W有W总,由“用滑轮或滑轮组提起同一重物”可知这几个装置的所做的有用功是相等的,η的高低就取决于W总;而W总=W有+W额外,使用滑轮或滑轮组时所做的额外功主要是克服动滑轮重和绳重、摩擦所做的功;
只有图B是一个定滑轮,在提升高度相等的条件下,额外功较少,总功也随之较少,有用功一定时,总功少,所以机械效率较高。故选B。
??6.【答案】C
【解析】解:
根据图示可知,n=2,拉力端移动的距离:s=2?=2×3m=6m;
A、不计绳重和摩擦,作用在绳子自由端的拉力:F=12(G+G动)=12×(380N+20N)=200N,故A错误;
B、拉力做的有用功:W有用=G?=380N×3m=1140J,故B错误;
C、总功:W总=Fs=200N×6m=1200J,
滑轮组的机械效率:
η=W有用W总=1140J1200J×100%=95%;故C正确;
D、不计绳重和摩擦,提升相同的物体,做相同有用功的情况下,动滑轮越重,额外功越大、总功越大,所以机械效率越低,故D错误。
故选:C。
7.【答案】D
【解析】解:由图知,n=3,绳子自由端移动的距离s=3?,滑轮组的机械效率η=W有用W总×100%=
G?Fs×100%=GnF×100%=g3F×100%,则拉力F=G3η=300N3×80%=125N,故A错误;拉力对滑轮组做的功:W总=Fs=125?N×6?m=750?J,故B错误;不计绳重和摩擦,拉力F=
13(G+G动),则动滑轮重力G动=3F?G=3×125?N?300?N=75?N,但实际上存在摩擦、绳重,则动滑轮的重力不是75?N,故C错误;拉力做功的功率:P=W总t=750J10s=75W,故D正确。
8.【答案】D
【解析】解:斜面高为h,物重为G,W有用=G?,又斜面长为L,拉力为F,W总=FL,则η=W有用W总×100%=G?FL×100%,而物体与斜面的摩擦力为f,W额外=fL,W总=W有用+W额外=G?+fL,η=W有用W总×100%=G?G?+fL×100%.
9.【答案】C
【解析】略
10.【答案】C
【解析】略
11.【答案】省功? 功的
【解析】解:有的机械可以省力,有的机械可以省距离,还有的机械还可以改变力的方向;但省力的机械必然费距离;省距离的机械一定费力;由功的原理可知,使用任何机械都不能省功,但使用机械有许多好处。
故答案为:省功;功的。
使用机械可以在省力、改变动力的方向或移动的距离上得到好处,给人们带来方便,做到方便快捷等;使用机械有这么多的好处,这正是人们使用机械的目的,但使用任何机械都不能省功。
12.【答案】50%
?变大
【解析】解:起重机克服建材重力做的功:W有用=G?=6000?N×3?m=1.8×104?J;起重机的机械效率:η=W有用W总×100%=1.8×104J3.6×104J×100%=50%;若只增加被提升的建材的重力,则有用功变大,额外功不变,根据η=W有用W总=W有用W有用+W额外=11+W额外W有用可知,起重机的机械效率会变大。
13.【答案】大于? 等于? 大于
【解析】解:绳重和摩擦力不计,由定滑轮的使用特点可知:F甲=G;
由动滑轮的使用特点可知:F乙=12(G动+G);
一般情况下,动滑轮重小于物重,因此F甲>F乙。
如图所示,用定滑轮和动滑轮分别将质量相同的甲、乙两物体匀速提升相同的高度,不计绳重与摩擦,则所做的有用功一样大,即拉力F对重物做的功W甲=W乙,
乙图,要克服动滑轮的重力做额外功,所以使用动滑轮做的总功多,由η=W有W总可知,动滑轮的机械效率低,即η甲>η乙。
故答案为:大于;等于;大于。
14.【答案】省力 80%
【解析】解:由独轮车的简化示意图可知,独轮车在使用时动力臂大于阻力臂,所以它属于省力杠杆;
由题可知L1:L2=s:?=3:1,
则杠杆的机械效率η=W有用W总×100%=G?Fs×100%=1200N×1500N×3×100%=80%。
15.【答案】(1)刻度尺;(2)88.9%;2.2;(3)变大;物重增加,轮和轴之间的压力变大,摩擦力变大?;(4)B?;(5)不变。
【解析】解:(1)实验时应沿竖直方向匀速缓慢拉动弹簧测力计,并用刻度尺测量出物体上升的高度;
(2)第2次实验的机械效率为η=W有用W总×100%=G?Fs×100%=4?N×0.1?m1.5?N×0.3?m×100%=88.9%,图丙中弹簧测力计分度值为0.2?N,示数为2.2?N,故编号②处数据为2.2;
(3)进一步分析数据,可知用同一滑轮组提升不同重物至同一高度,提升的物重增加时,所做的额外功将变大,因为物重增加,轮和轴之间的压力变大,摩擦力变大;
(4)动滑轮重力不可忽略,则克服动滑轮重和绳与滑轮、滑轮与轴间的摩擦所做的功为额外功,物重增大,有用功逐渐增大,有用功占总功的比值在增大,所以机械效率逐渐增大,但从摩擦角度考虑,随着物体重力的增加,滑轮与绳子间摩擦会有一定程度增大,故机械效率η与物体重力G的关系并不成正比,故B符合题意;
(5)不计绳重及摩擦,则克服动滑轮的自重做功为额外功的唯一来源,若将此滑轮组换一种绕绳方法,提升相同的物体时,滑轮组的机械效率η=W有用W总×100%=W有用W有用+W额外×100%=G物?(G物+G动)?×100%=G物G物+G动×100%,因G物和G动不变,故滑轮组的机械效率不变。
【答案】刻度尺? 71.4%? 机械效率越高
【解析】解:(1)要测量斜面的高度和木块沿斜面移动的距离就要使用长度的测量工具---刻度尺。
(2)第3次实验时,有用功W有=G?=5N×0.3m=1.5J,
总功W总=Fs=4.2N×0.5m=2.1J,
斜面的机械效率η=η=W有W总×100%=1.5J2.1J×100%≈71.4%。
(3)由图中数据可知:斜面的倾斜程度越大,斜面的机械效率越高
故答案为:(1)刻度尺;(2)71.4%;(3)机械效率越高。
17.【答案】(1)①2mg?Fs×100%?②>?③【解析】解:(1)①在实验过程中,有用功W有用=G?=2mg?,总功W总=Fs,所以杠杆的机械效率η=W有用W总×100%=2mg?Fs×100%。
②将三个相同的钩码悬挂在A点匀速提高时,所做的额外功相同,有用功增加,即有用功占总功的比例变大,所以此时杠杆的机械效率变大,即η2>η1。
③将同一物体由悬挂的A点变为B点时,阻力臂变大,由杠杆的平衡条件可知拉力F变大,杠杆提升的高度减小,额外功减小,因此有用功占总功的比例变大,杠杆的机械效率变大,即ηA<ηB。
(2)若将同一物体悬挂在A点,弹簧测力计分别挂在C点和D点时,竖直向上匀速使物体提高相同高度时,所做的有用功相同,额外功也相同,故总功相同,根据机械效率公式可知,机械效率相同,ηC=ηD。
18.【答案】(1)①越重;②2和3;③乙;绳子的有效段数为1;
(2)减小接触面的粗糙程度;
(3)不省功;B
【解析】
(1)①比较1和2两次实验发现:在所用滑轮组相同时,提升物体的重力越大,机械效率越高,即所用滑轮组一定时,提升的钩码重力越大,机械效率越高;
②比较2和3两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关;
③第5次实验室利用了图乙的装置完成的,判断依据是:n=s?=0.2m0.2m=1,即绳子的有效段数为1;
(2)保持斜面倾斜程度不变,可以采用减小接触面粗糙程度的方法减小摩擦,从而提高斜面的机械效率;
(3)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功,可见使用任何机械都不省功,采用了实验推理法,而焦耳定律、阿基米德原理、欧姆定律可通过实验直接验证,故ACD不合题意;牛顿第一定律不能用实验直接验证,是在实验的基础下推理得出的,故B符合题意。
故选B。
故答案为:(1)①越重;②2和3;③乙;绳子的有效段数为1;(2)减小接触面的粗糙程度;(3)不省功;B。
同课章节目录
- 第十一章 机械功与机械能
- 11.1 怎样才叫做功
- 11.2 怎样比较做功的快慢
- 11.3 如何提高机械效率
- 11.4 认识动能和势能
- 第十二章 内能与热机
- 12.1 认识内能
- 12.2 热量和热值
- 12.3 研究物质的比热容
- 12.4 热机与社会发展
- 第十三章 探究简单电路
- 13.1 从闪电谈起
- 13.2 电路的组成和连接方式
- 13.3 怎样认识和测量电流
- 13.4 探究串、并联电路中的电流
- 13.5 怎样认识和测量电压
- 13.6 探究串、并联电路中的电压
- 第十四章 探究欧姆定律
- 14.1 怎样认识电阻
- 14.2 探究欧姆定律
- 14.3 欧姆定律的应用
- 第十五章 电能与电功率
- 15.1 电能与电功
- 15.2 认识电功率
- 15.3 怎样使用电器正常工作
- 15.4 探究焦耳定律
