23.1图形的旋转(第2课时) 课件(共21张PPT)
文档属性
| 名称 | 23.1图形的旋转(第2课时) 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 14:38:44 | ||
图片预览




文档简介
(共21张PPT)
23.1图形的旋转
---第2课时
人教版
九年级上
教学目标
1.能够根据旋转的基本性质进行简单作图.(重点)
2.能根据旋转的性质制作美丽的图案。
回顾旧知
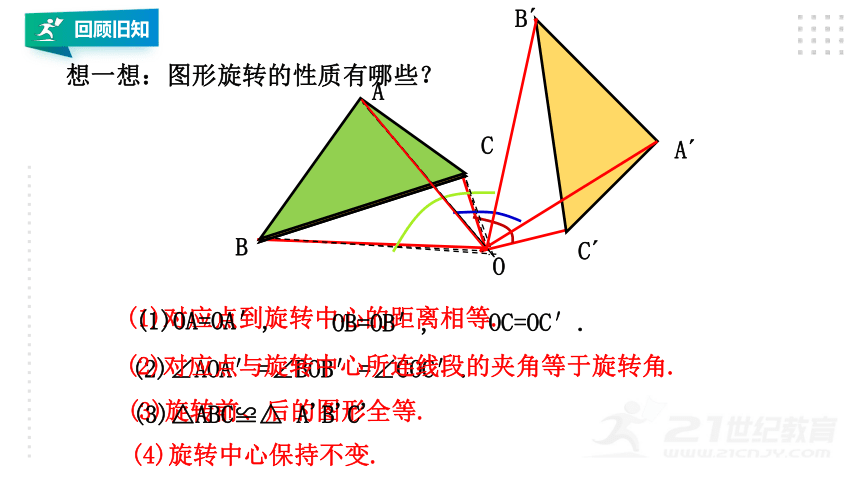
(3)旋转前、后的图形全等.
(3)△ABC≌△
A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
(1)对应点到旋转中心的距离相等.
(1)OA=OA′,
B
A
B?
A?
C
C?
(2)对应点与旋转中心所连线段的夹角等于旋转角.
OB=OB′,
OC=OC′.
O
(4)旋转中心保持不变.
想一想:图形旋转的性质有哪些?
合作探究
探究一:作简单图形的旋转
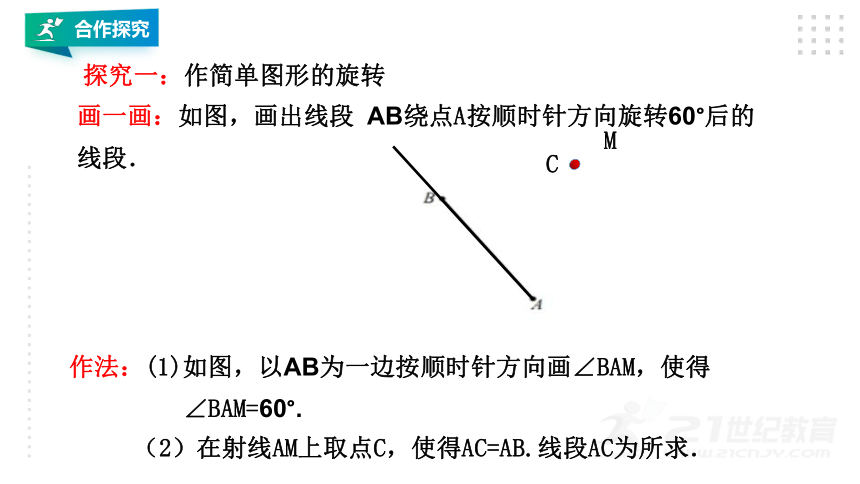
画一画:如图,画出线段
AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAM,使得
∠BAM=60°.
M
C
(2)在射线AM上取点C,使得AC=AB.线段AC为所求.
合作探究
A
B
O
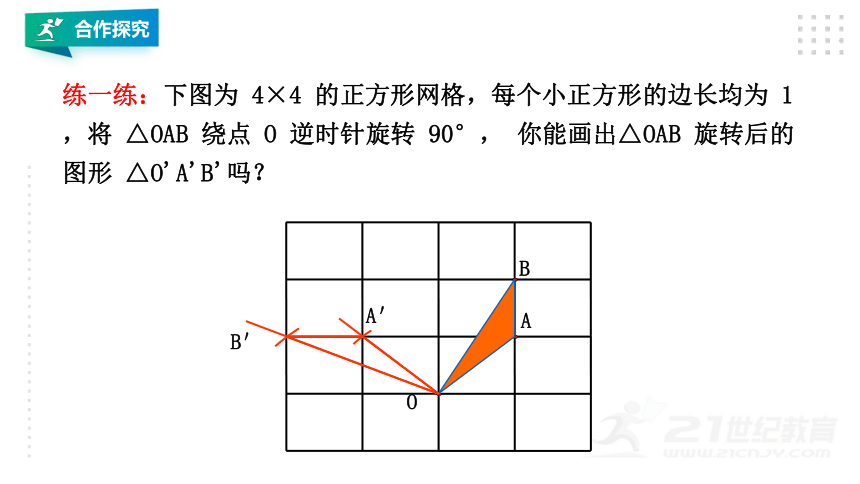
练一练:下图为
4×4
的正方形网格,每个小正方形的边长均为
1,将
△OAB
绕点
O
逆时针旋转
90°,
你能画出△OAB
旋转后的图形
△O'A'B'吗?
A'
B'
典例精析
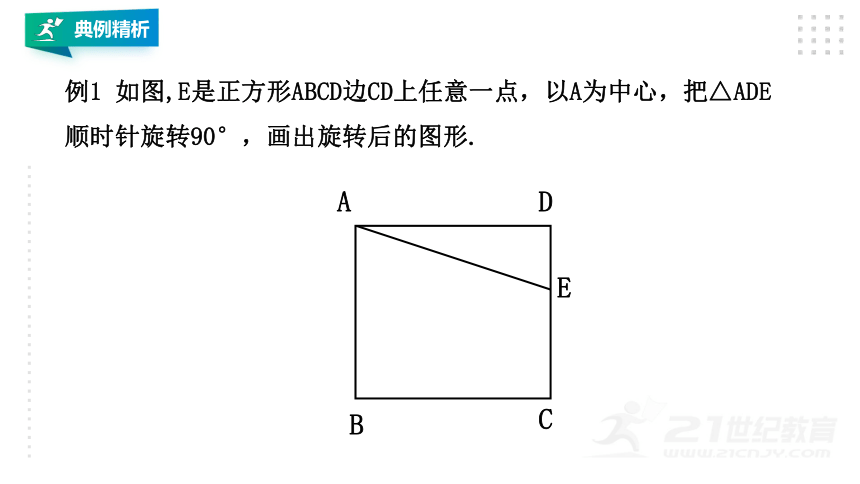
例1
如图,E是正方形ABCD边CD上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A
B
C
D
E
典例精析
A
B
C
E
D
E′
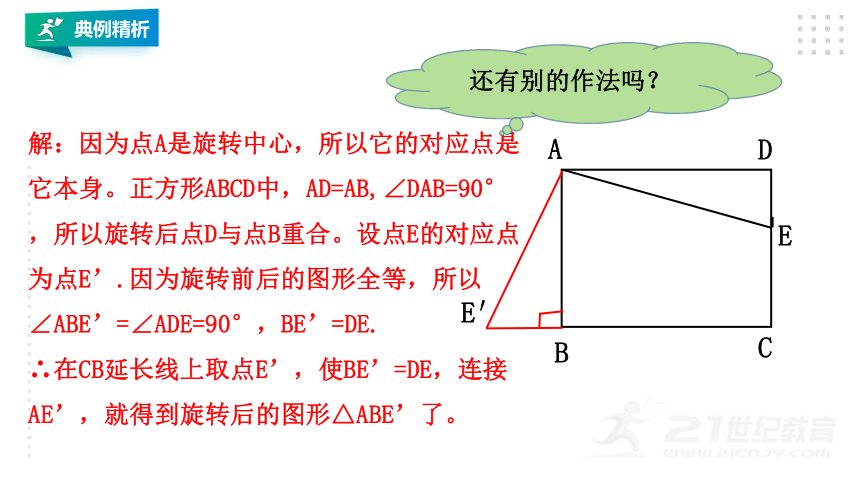
解:因为点A是旋转中心,所以它的对应点是它本身。正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合。设点E的对应点为点E’.因为旋转前后的图形全等,所以∠ABE’=∠ADE=90°,BE’=DE.
∴在CB延长线上取点E’,使BE’=DE,连接AE’,就得到旋转后的图形△ABE’了。
还有别的作法吗?
典例精析
A
B
C
E
D
E′
合作探究
(1)明确旋转三要素:旋转中心、旋转方向和旋转角度.
归纳总结:旋转作图的基本步骤:
(2)找出关键点;
(3)作出关键点的对应点;
(4)作出新图形;
(5)写出结论.
1、如图,点A,C的坐标分别为(1,1),(2,4),将△ABC绕点A按逆时针方向旋转90°,得到△AB'C',则点C的对应点C'的坐标为( )
A.(-2,4)
B.(4,0)
C.(-1,3)
D.(-2,2)
D
趁热打铁
趁热打铁
2、画出下图所示的四边形
ABCD
以
O为中心,顺时针旋转
60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
合作探究
探究二:运用图形的旋转设计图案
1.选择不同的__________、不同的
旋转同一个图案,会出现不同的效果.
(1)两个旋转中,旋转中心不变,
改变了,产生了_______的旋转效果.
(2)两个旋转中,旋转角不变,__________改变了,
产生了_______的旋转效果.
o
旋转中心
旋转角
旋转角
不同
旋转中心
不同
α
o
合作探究
2.我们可以借助旋转可以设计出许多美丽的图案.
综合演练
1、如图,该图形在绕中心点O按下列角度旋转后,不能与其自身重合的是( )
A.72°
B.144°
C.108°
D.216°
C
综合演练
2.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,12)
B.(-2,0)
C.(2,12)或(-2,0)
D.(12,2)或(-2,0)
知识点拨:要注意分顺时针旋转和逆时针旋转两种情况讨论解答.
C
综合演练
3.等边三角形绕着它的中心O旋转,若旋转后的三角形能与自身重合,则旋转角最小是( )
A.360°
B.240°
C.120°
D.60°
C
4.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,
旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小
是( )
A.68°
B.20°
C.28°
D.22°
D
综合演练
3.如图,平面直角坐标系中,已知△ABC的顶点A的坐标为(-1,2).(1)将△ABC向右平移3个单位得到△DEF,请在图中画出平移后的图形;
(2)将△ABC绕点C按逆时针方
向旋转90°后得到△MNC,请在
图中画出旋转后的图形,并写出
点M,N的坐标.
解:(1)如图,△DEF为所作;
(2)如图,△MNC为所作,
M(-3,-2),N(-2,-4).
课堂总结
说一说如何根据已知条件作图形的旋转。
本节课你有哪些收获?
作业布置
练习
P61页:1、2、3
https://www.21cnjy.com/help/help_extract.php
23.1图形的旋转
---第2课时
人教版
九年级上
教学目标
1.能够根据旋转的基本性质进行简单作图.(重点)
2.能根据旋转的性质制作美丽的图案。
回顾旧知
(3)旋转前、后的图形全等.
(3)△ABC≌△
A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
(1)对应点到旋转中心的距离相等.
(1)OA=OA′,
B
A
B?
A?
C
C?
(2)对应点与旋转中心所连线段的夹角等于旋转角.
OB=OB′,
OC=OC′.
O
(4)旋转中心保持不变.
想一想:图形旋转的性质有哪些?
合作探究
探究一:作简单图形的旋转
画一画:如图,画出线段
AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAM,使得
∠BAM=60°.
M
C
(2)在射线AM上取点C,使得AC=AB.线段AC为所求.
合作探究
A
B
O
练一练:下图为
4×4
的正方形网格,每个小正方形的边长均为
1,将
△OAB
绕点
O
逆时针旋转
90°,
你能画出△OAB
旋转后的图形
△O'A'B'吗?
A'
B'
典例精析
例1
如图,E是正方形ABCD边CD上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A
B
C
D
E
典例精析
A
B
C
E
D
E′
解:因为点A是旋转中心,所以它的对应点是它本身。正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合。设点E的对应点为点E’.因为旋转前后的图形全等,所以∠ABE’=∠ADE=90°,BE’=DE.
∴在CB延长线上取点E’,使BE’=DE,连接AE’,就得到旋转后的图形△ABE’了。
还有别的作法吗?
典例精析
A
B
C
E
D
E′
合作探究
(1)明确旋转三要素:旋转中心、旋转方向和旋转角度.
归纳总结:旋转作图的基本步骤:
(2)找出关键点;
(3)作出关键点的对应点;
(4)作出新图形;
(5)写出结论.
1、如图,点A,C的坐标分别为(1,1),(2,4),将△ABC绕点A按逆时针方向旋转90°,得到△AB'C',则点C的对应点C'的坐标为( )
A.(-2,4)
B.(4,0)
C.(-1,3)
D.(-2,2)
D
趁热打铁
趁热打铁
2、画出下图所示的四边形
ABCD
以
O为中心,顺时针旋转
60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
合作探究
探究二:运用图形的旋转设计图案
1.选择不同的__________、不同的
旋转同一个图案,会出现不同的效果.
(1)两个旋转中,旋转中心不变,
改变了,产生了_______的旋转效果.
(2)两个旋转中,旋转角不变,__________改变了,
产生了_______的旋转效果.
o
旋转中心
旋转角
旋转角
不同
旋转中心
不同
α
o
合作探究
2.我们可以借助旋转可以设计出许多美丽的图案.
综合演练
1、如图,该图形在绕中心点O按下列角度旋转后,不能与其自身重合的是( )
A.72°
B.144°
C.108°
D.216°
C
综合演练
2.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,12)
B.(-2,0)
C.(2,12)或(-2,0)
D.(12,2)或(-2,0)
知识点拨:要注意分顺时针旋转和逆时针旋转两种情况讨论解答.
C
综合演练
3.等边三角形绕着它的中心O旋转,若旋转后的三角形能与自身重合,则旋转角最小是( )
A.360°
B.240°
C.120°
D.60°
C
4.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,
旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小
是( )
A.68°
B.20°
C.28°
D.22°
D
综合演练
3.如图,平面直角坐标系中,已知△ABC的顶点A的坐标为(-1,2).(1)将△ABC向右平移3个单位得到△DEF,请在图中画出平移后的图形;
(2)将△ABC绕点C按逆时针方
向旋转90°后得到△MNC,请在
图中画出旋转后的图形,并写出
点M,N的坐标.
解:(1)如图,△DEF为所作;
(2)如图,△MNC为所作,
M(-3,-2),N(-2,-4).
课堂总结
说一说如何根据已知条件作图形的旋转。
本节课你有哪些收获?
作业布置
练习
P61页:1、2、3
https://www.21cnjy.com/help/help_extract.php
同课章节目录
