北京市四中2011-2012学年七年级下学期期中考试数学试题
文档属性
| 名称 | 北京市四中2011-2012学年七年级下学期期中考试数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-31 00:00:00 | ||
图片预览


文档简介
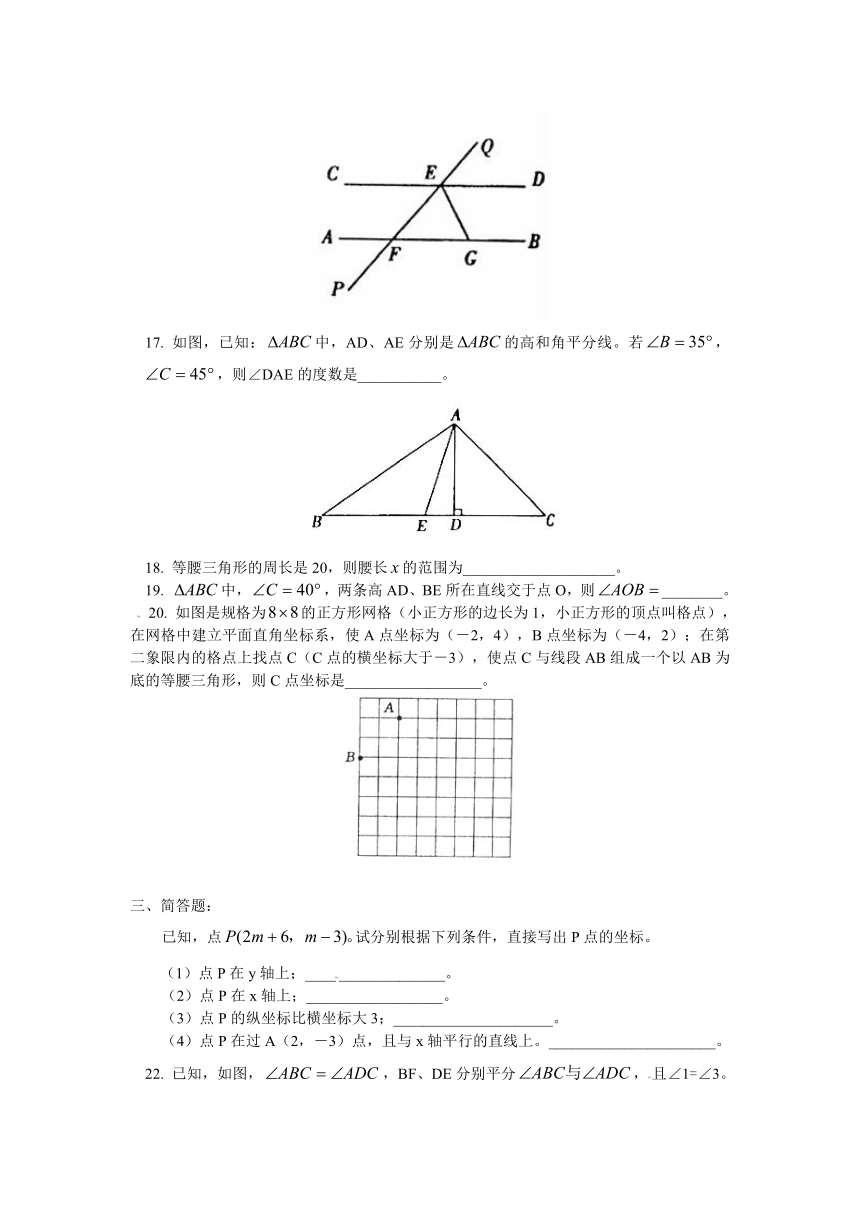
北京四中2011-2012学年度第二学期期中考试初一数学试卷
(考试时间100分钟,试卷满分100分)
一、选择题
1. 已知点A(1,2),AC⊥x轴于点C,则点C的坐标为( )。
A. (1,0) B. (2,0) C. (0,2) D. (0,1)
2. 如图,在数轴上表示的解集对应的不等式是( )。
A. B.
C. D.
3. 在下面四种正多边形中,用同一种图形不能平面镶嵌的是( )。
4. 已知,点P为直线m外一点,点P到直线m上的三点A、B、C的距离分别为PA=4cm,PB=6cm,PC=3cm,则点P到直线m的距离为( )。
A. 3cm B. 小于3cm C. 不大于3cm D. 不确定
5. 已知二元一次方程,当时,的取值范围是( )。
A. B. C. D.
6. 将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1);(2) (3);(4)
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
A. B. C. 3 D. 4
7. 如图,AB∥DE,那么=( )。
A. B. C. D.
8. 如图,已知△ABC的面积为36,将△ABC沿BC平移到△A′B′C′,使B′和C重合,连结AC′交A′C于D,则△C′AC的面积为( )。
A. 9 B. 12 C. 18 D. 36
9. 若不等式组的解集是,则的取值范围是( )。
A. m<2 B. C. D.
10. 如图△ABC中,,外角的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度。
A. 4 B. 5 C. 6 D. 7
二、填空题
11. 若点在第四象限,则的取值范围是____________。
12. 不等式的解集为,则的值是________。
13. 在平面直角坐标系中,已知,B(1,1),将线段AB平移后,A点的坐标变为(-2,1),则点B的坐标变为_____________。
14. 在平面直角坐标系中,在轴上到轴距离为3的点的坐标是___________________。
15. 对于,若BC边不动,点A在所在平面内竖直向上运动,∠A越来越小,∠B,∠C越来越大。若∠A减少度,∠B增加度,∠C增加度,则,三者之间的数量关系是_________。
16. 如图,AB∥CD,直线PQ分别交AB、CD于点E、F,EG是∠FED的平分线,交AB于点G。若,那么∠EGB等于____。
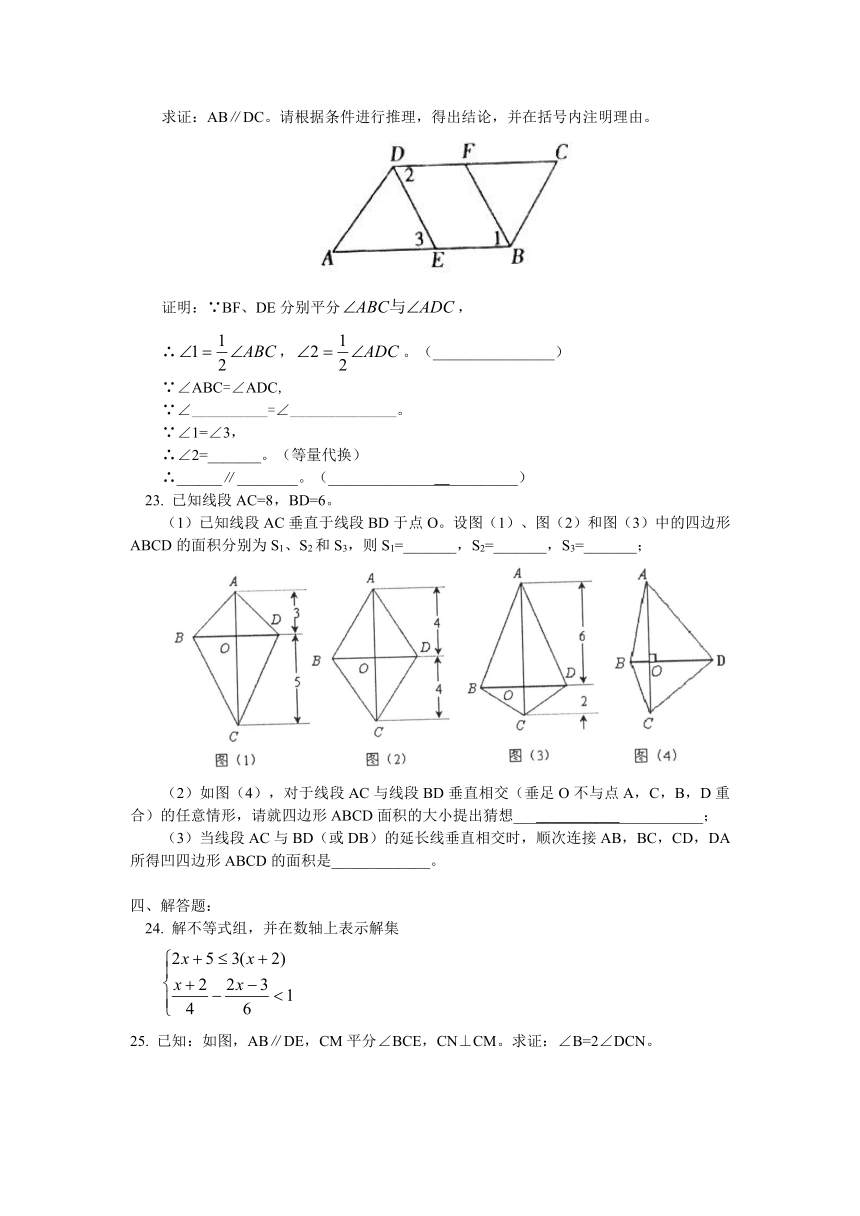
17. 如图,已知:中,AD、AE分别是的高和角平分线。若,,则∠DAE的度数是___________。
18. 等腰三角形的周长是20,则腰长的范围为____________________。
19. 中,,两条高AD、BE所在直线交于点O,则________。
20. 如图是规格为的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是__________________。
三、简答题:
已知,点试分别根据下列条件,直接写出P点的坐标。
(1)点P在y轴上;__________________。
(2)点P在x轴上;__________________。
(3)点P的纵坐标比横坐标大3;_____________________。
(4)点P在过A(2,-3)点,且与x轴平行的直线上。______________________。
22. 已知,如图,,BF、DE分别平分,且∠1=∠3。
求证:AB∥DC。请根据条件进行推理,得出结论,并在括号内注明理由。
证明:∵BF、DE分别平分,
∴,。(________________)
∵∠ABC=∠ADC,
∵∠__________=∠______________。
∵∠1=∠3,
∴∠2=_______。(等量代换)
∴______∥________。(_________________________)
23. 已知线段AC=8,BD=6。
(1)已知线段AC垂直于线段BD于点O。设图(1)、图(2)和图(3)中的四边形ABCD的面积分别为S1、S2和S3,则S1=_______,S2=_______,S3=_______;
(2)如图(4),对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,请就四边形ABCD面积的大小提出猜想_________________________;
(3)当线段AC与BD(或DB)的延长线垂直相交时,顺次连接AB,BC,CD,DA所得凹四边形ABCD的面积是_____________。
四、解答题:
24. 解不等式组,并在数轴上表示解集
25. 已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM。求证:∠B=2∠DCN。
26. 启明中学因教室改造计划购买A、B两种型号的小黑板,经市场调查,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?
(2)根据学校实际情况,需购买A、B两种型号的小黑板共60块,要求购买A、B
两种型号小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、
B种型号小黑板总数量的。请你通过计算,求出启明中学购买A、B两种型号的小黑
板有哪几种方案?
27. 如图,在平面直角坐标系内放置一个直角梯形AOCD,已知AD=3,AO=8,OC=5。
(1)若点P在轴上且S□PAD=S□poc,求点P的坐标;
(2)若点P在梯形内且S□PAD=S□POC,S□PAO=S□PCD,求点P的坐标。
28. 如图,已知CD∥AF,,,,,求的大小。
附加题:
1. 同时满足,,则的取值范围是_____________。
2. 把一个多边形沿着几条直线剪开,分割成若干个多边形。分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍。
求:(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
【试题答案】
一、1. A; 2.B; 3. C; 4. C; 5. A; 6. D; 7. C; 8. D; 9. C;10. B.
二、11. ; 12. 2; 13. (0,0); 14. (-3,0)或(3,0);
15.; 16. ; 17. ; 18. ;19. ; 20.(-2,2)或(-1,1)。
三、简答题
21. (1)P(0,-6);(2)P(12,0)(3)P(-18,-15);(4)(6,-3)
22. 角平分线定义;1;2;∠3;AB;CD;内错角相等,两直线平行。
23. (1)24;24;24。
(2)四边形ABCD的面积=24
(3)24.
四、解答题
24. 不等式组的解集为。图略。
25. 证明:
平分
AB∥DE
26. 解:(1)设购买一块A型小黑板需要元,则购买一块B型小黑板需要元。根据题意解得……
答:购买一块A型小黑板需要100元,购买一块B型小黑板需要80元
(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块。
根据题意①
② 解得
m为整数。 m为21或22
当m=21时;当时。有两种购买方案
方案一:购买A型小黑板21块,购买B型小黑板39块;
方案二:购买A型小黑板22块。购买B型小黑板38块。
27. 解:(1)P(0,3)或P(0,-12);
(2)过点P作PE⊥y轴于E,
如图所示,。
即,得OE=3。
。
。 。
P点的坐标是
28. 解:连结AD
∵CD∥AF
在四边形ABCD与四边形ADEF中
∵AB⊥BC
,
附加题:
1.
2. 把多边形沿直线剪开,每增加一个多边形,边数的增加会出现以下三种情况:①当直线经过两个顶点时,增加两条边;②当直线经过一个顶点时,增加三条边;③当直线不经过顶点时,增加四条边。于是,当将原多边形分割成4个小多边形,最多可以增加条边,当将原多边形分割成8个小多边形,最少可以增加2×7=14条边。所以分割后的多边形的个数是5,6,7中的一个。
设原多边形的边数是n,分割成边数为的m个多边形,则m个多边形的总边数为由题意,有
∴m是3的倍数
于是m=6,n=12。
原来的多边形是12边形,把原来的多边形分割成了6个小多边形。
(考试时间100分钟,试卷满分100分)
一、选择题
1. 已知点A(1,2),AC⊥x轴于点C,则点C的坐标为( )。
A. (1,0) B. (2,0) C. (0,2) D. (0,1)
2. 如图,在数轴上表示的解集对应的不等式是( )。
A. B.
C. D.
3. 在下面四种正多边形中,用同一种图形不能平面镶嵌的是( )。
4. 已知,点P为直线m外一点,点P到直线m上的三点A、B、C的距离分别为PA=4cm,PB=6cm,PC=3cm,则点P到直线m的距离为( )。
A. 3cm B. 小于3cm C. 不大于3cm D. 不确定
5. 已知二元一次方程,当时,的取值范围是( )。
A. B. C. D.
6. 将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1);(2) (3);(4)
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
A. B. C. 3 D. 4
7. 如图,AB∥DE,那么=( )。
A. B. C. D.
8. 如图,已知△ABC的面积为36,将△ABC沿BC平移到△A′B′C′,使B′和C重合,连结AC′交A′C于D,则△C′AC的面积为( )。
A. 9 B. 12 C. 18 D. 36
9. 若不等式组的解集是,则的取值范围是( )。
A. m<2 B. C. D.
10. 如图△ABC中,,外角的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度。
A. 4 B. 5 C. 6 D. 7
二、填空题
11. 若点在第四象限,则的取值范围是____________。
12. 不等式的解集为,则的值是________。
13. 在平面直角坐标系中,已知,B(1,1),将线段AB平移后,A点的坐标变为(-2,1),则点B的坐标变为_____________。
14. 在平面直角坐标系中,在轴上到轴距离为3的点的坐标是___________________。
15. 对于,若BC边不动,点A在所在平面内竖直向上运动,∠A越来越小,∠B,∠C越来越大。若∠A减少度,∠B增加度,∠C增加度,则,三者之间的数量关系是_________。
16. 如图,AB∥CD,直线PQ分别交AB、CD于点E、F,EG是∠FED的平分线,交AB于点G。若,那么∠EGB等于____。
17. 如图,已知:中,AD、AE分别是的高和角平分线。若,,则∠DAE的度数是___________。
18. 等腰三角形的周长是20,则腰长的范围为____________________。
19. 中,,两条高AD、BE所在直线交于点O,则________。
20. 如图是规格为的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是__________________。
三、简答题:
已知,点试分别根据下列条件,直接写出P点的坐标。
(1)点P在y轴上;__________________。
(2)点P在x轴上;__________________。
(3)点P的纵坐标比横坐标大3;_____________________。
(4)点P在过A(2,-3)点,且与x轴平行的直线上。______________________。
22. 已知,如图,,BF、DE分别平分,且∠1=∠3。
求证:AB∥DC。请根据条件进行推理,得出结论,并在括号内注明理由。
证明:∵BF、DE分别平分,
∴,。(________________)
∵∠ABC=∠ADC,
∵∠__________=∠______________。
∵∠1=∠3,
∴∠2=_______。(等量代换)
∴______∥________。(_________________________)
23. 已知线段AC=8,BD=6。
(1)已知线段AC垂直于线段BD于点O。设图(1)、图(2)和图(3)中的四边形ABCD的面积分别为S1、S2和S3,则S1=_______,S2=_______,S3=_______;
(2)如图(4),对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,请就四边形ABCD面积的大小提出猜想_________________________;
(3)当线段AC与BD(或DB)的延长线垂直相交时,顺次连接AB,BC,CD,DA所得凹四边形ABCD的面积是_____________。
四、解答题:
24. 解不等式组,并在数轴上表示解集
25. 已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM。求证:∠B=2∠DCN。
26. 启明中学因教室改造计划购买A、B两种型号的小黑板,经市场调查,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?
(2)根据学校实际情况,需购买A、B两种型号的小黑板共60块,要求购买A、B
两种型号小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、
B种型号小黑板总数量的。请你通过计算,求出启明中学购买A、B两种型号的小黑
板有哪几种方案?
27. 如图,在平面直角坐标系内放置一个直角梯形AOCD,已知AD=3,AO=8,OC=5。
(1)若点P在轴上且S□PAD=S□poc,求点P的坐标;
(2)若点P在梯形内且S□PAD=S□POC,S□PAO=S□PCD,求点P的坐标。
28. 如图,已知CD∥AF,,,,,求的大小。
附加题:
1. 同时满足,,则的取值范围是_____________。
2. 把一个多边形沿着几条直线剪开,分割成若干个多边形。分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍。
求:(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
【试题答案】
一、1. A; 2.B; 3. C; 4. C; 5. A; 6. D; 7. C; 8. D; 9. C;10. B.
二、11. ; 12. 2; 13. (0,0); 14. (-3,0)或(3,0);
15.; 16. ; 17. ; 18. ;19. ; 20.(-2,2)或(-1,1)。
三、简答题
21. (1)P(0,-6);(2)P(12,0)(3)P(-18,-15);(4)(6,-3)
22. 角平分线定义;1;2;∠3;AB;CD;内错角相等,两直线平行。
23. (1)24;24;24。
(2)四边形ABCD的面积=24
(3)24.
四、解答题
24. 不等式组的解集为。图略。
25. 证明:
平分
AB∥DE
26. 解:(1)设购买一块A型小黑板需要元,则购买一块B型小黑板需要元。根据题意解得……
答:购买一块A型小黑板需要100元,购买一块B型小黑板需要80元
(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块。
根据题意①
② 解得
m为整数。 m为21或22
当m=21时;当时。有两种购买方案
方案一:购买A型小黑板21块,购买B型小黑板39块;
方案二:购买A型小黑板22块。购买B型小黑板38块。
27. 解:(1)P(0,3)或P(0,-12);
(2)过点P作PE⊥y轴于E,
如图所示,。
即,得OE=3。
。
。 。
P点的坐标是
28. 解:连结AD
∵CD∥AF
在四边形ABCD与四边形ADEF中
∵AB⊥BC
,
附加题:
1.
2. 把多边形沿直线剪开,每增加一个多边形,边数的增加会出现以下三种情况:①当直线经过两个顶点时,增加两条边;②当直线经过一个顶点时,增加三条边;③当直线不经过顶点时,增加四条边。于是,当将原多边形分割成4个小多边形,最多可以增加条边,当将原多边形分割成8个小多边形,最少可以增加2×7=14条边。所以分割后的多边形的个数是5,6,7中的一个。
设原多边形的边数是n,分割成边数为的m个多边形,则m个多边形的总边数为由题意,有
∴m是3的倍数
于是m=6,n=12。
原来的多边形是12边形,把原来的多边形分割成了6个小多边形。
同课章节目录
