2012年中考复习--存在型问题

存在型问题
存在型问题是近几年来全国各地中考的热点。这类问题的知识面覆盖面积广，综合性强，
题型构思精巧，解题方法灵活，对考生分析问题和解决问题的能力要求较高。其特点就是在一定的条件下探究发现某些数学结论或者规律是否存在，由于结论有存在或者不存在两种情况，所以具有开放性，解题时常常要猜想或者假设问题的某种关系或结论存在，再经过分析、归纳、演算、推理，找出最后答案。
三角形的存在问题
例1）、（2011 江苏盐城）（本题满分12分）如图，已知一次函数y = - x +7与正比例函数y = x的图象交于点A，
且与x轴交于点B.
（1）求点A和点B的坐标； A(3，4) . B（7，0）.
（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．
动点P从点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒.
①当t为何值时，以A、P、R为顶点的三角形的面积为8？ t =2
②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不
存在，请说明理由． t=1或 或5或 时
【分析】（1）联立方程y = - x +7和y = x即可求出点A的坐标，今y=-x+7=0即可得点B的坐标。
（2）①只要把三角形的面积用t表示，求出即可。应注意分P在OC上运动和P在CA上运动两种情况了。
②只要把有关线段用t表示，找出AP=AQ，AP=PQ，AQ=PQ的条件时t的值即可。应注意分别讨论P在OC上运动（此时直线l与AB相交）和P在CA上运动（此时直线l与AO相交）时AP=AQ，AP=PQ，AQ=PQ的条件。
总结
1/一次函数，二元一次方程组，勾股定理，三角函数，一元二次方程，等腰三角形。
2/ 解决这类问题的一般思路是假设存在-----推理论证------得出结论。值得注意的是如果最后得出的结论与已知条件、某个定理、相符合，就存在，否则就不存在。
与四边形有关的存在型问题
如图，在平面直角坐标系中，直线与交于点，分别交轴于点和点，点是直线上的一个动点．
（1）求点的坐标． B C（4，0） A
（2）当为等腰三角形时，求点的坐标．
（3）在直线上是否存在点，使得以点为顶点的四边形是平行四边形？如果存在，直线写出的值；如果不存在，请说明理由．
分析
在解决与等腰三角形有关的问题时，在没有标明顶角与底角的情况下，都有分类讨论。
在解决坐标平面内的平行四边形的问题应该注意对边平行这一性质，寻找坐标系中平行线之间的关系，还可以构造相似三角形，结合勾股定理解决问题。
与面积有关的存在型问题
例3 2011 江苏南通）如图，已知直线l经过点A(1，0)，与双曲线y＝
(x＞0)交于点B(2，1)．过点P(p，p－1)(p＞1)作x轴的平
行线分别交双曲线y＝(x＞0)和y＝－(x＜0)于点M、N．
(1)求m的值和直线l的解析式；
(2)若点P在直线y＝2上，求证：△PMB∽△PNA；
(3)是否存在实数p，使得S△AMN＝4S△AMP？若存在，请求出所有满足条件的p的值；若
不存在，请说明理由．
【分析】(1)用点B(2，1)的坐标代入y＝即可得m值，用待定系数法，求解二元一次方程组可得直线l的解析式。
(2)点P(p，p－1)在直线y＝2上，实际上表示了点是直线y＝2和l的交点，这样要求证△PMB∽△PNA只要证出对应线段成比例即可。
(3)首先要考虑点P的位置。实际上，当p＝3时，易求出这时S△AMP＝S△AMN，当p>3时，注意到这时S△AMP大于p＝3时的三角形面积，从而大于S△AMN，。所以只要主要研究当1＜p＜3时的情况。作出必要的辅助线后，先求直线MP的方程，再求出各点坐标（用p表示），然后求出面积表达式，代入S△AMN＝4S△AMP后求出p值。
总结
反比例函数，一次函数，待定系数法，二元一次方程组，勾股定理，相似三角形一元二次方程
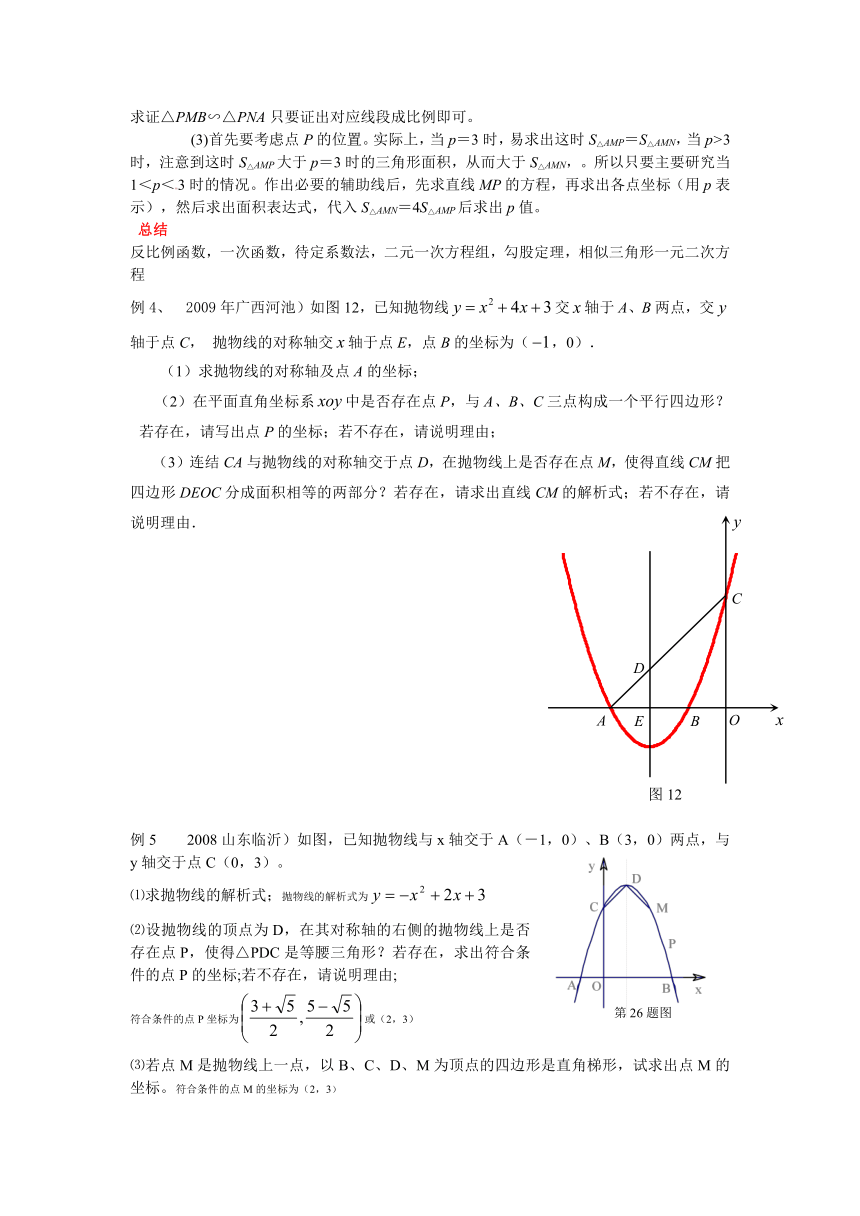
例4、 2009年广西河池）如图12，已知抛物线交轴于A、B两点，交轴于点C，抛物线的对称轴交轴于点E，点B的坐标为（，0）．
（1）求抛物线的对称轴及点A的坐标；
（2）在平面直角坐标系中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；
（3）连结CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．
例5 2008山东临沂）如图，已知抛物线与x轴交于A（－1，0）、B（3，0）两点，与y轴交于点C（0，3）。
⑴求抛物线的解析式；抛物线的解析式为
⑵设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标;若不存在，请说明理由;
符合条件的点P坐标为或（2，3）
⑶若点M是抛物线上一点，以B、C、D、M为顶点的四边形是直角梯形，试求出点M的坐标。符合条件的点M的坐标为（2，3）
分析
第二问假设存在，但没有说明是那两条相等，所以应分为已知边为腰和底两种情况讨论。
第三问应该注意已有三个固定点了，分别考虑已知的三条线段为梯形的底边的情况，注意不重也不漏就行了
练习
1）如图, 已知抛物线与y轴相交于C，与x轴相交于A、B，点A的坐标为（2，0），点C的坐标为（0，-1）.
（1）求抛物线的解析式；
（2）点E是线段AC上一动点，过点E作DE⊥x轴于点D，连结DC，当△DCE的面积最大时，求点D的坐标；
（3）在直线BC上是否存在一点P，使△ACP为等腰三角形，若存在，求点P的坐标，若不存在，说明理由.
2）如图：二次函数y=﹣x2 + ax + b的图象与x轴交于A（-，0），B（2，0）两点，且与y轴交于点C．
（1）求该抛物线的解析式，并判断△ABC的形状；
（2）在x轴上方的抛物线上有一点D，且A、C、D、B四点为顶点的四边形是等腰梯形，请直接写出D点的坐标；
（3）在此抛物线上是否存在点P，使得以A、C、B、P四点为顶点的四边形是直角梯形？若存在，求出P点的坐标；若不存在，说明理由．
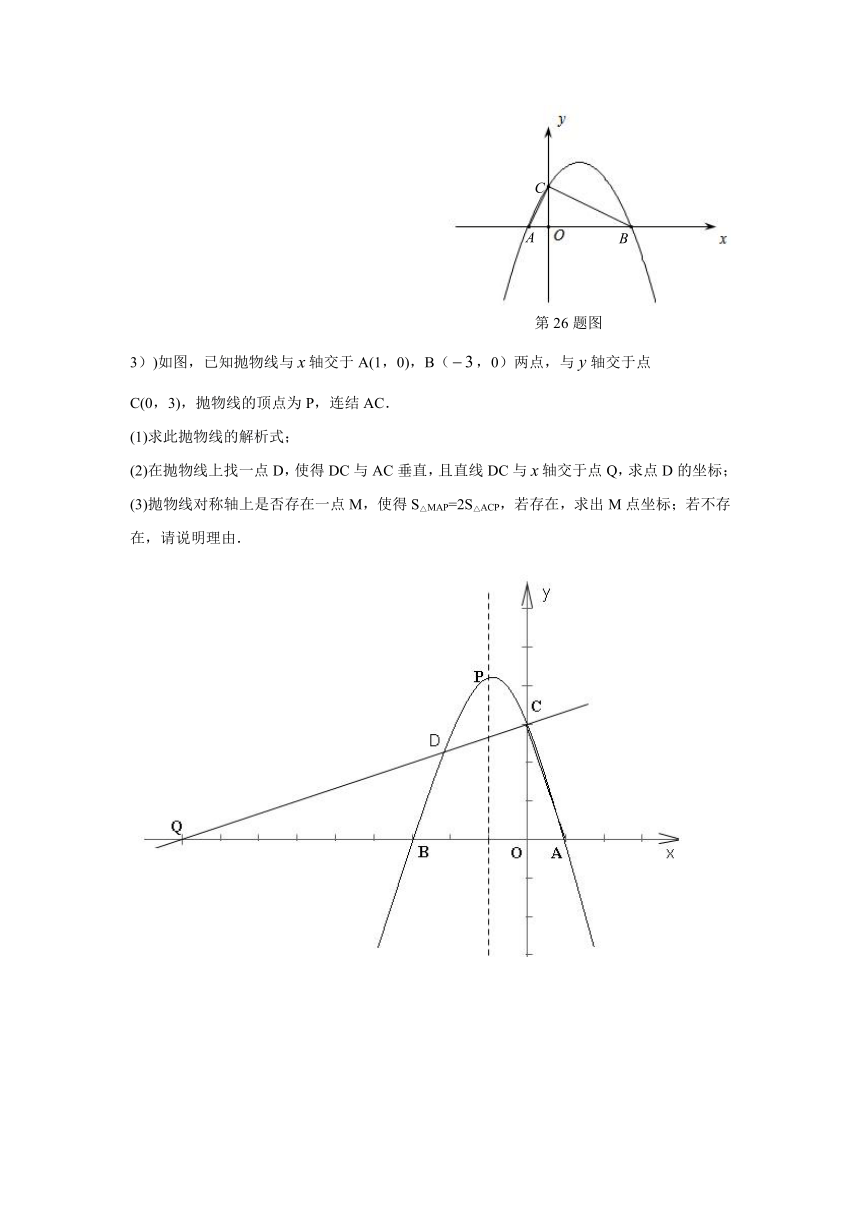
3）)如图，已知抛物线与轴交于A(1，0)，B（，0）两点，与轴交于点
C(0，3)，抛物线的顶点为P，连结AC．
(1)求此抛物线的解析式；
(2)在抛物线上找一点D，使得DC与AC垂直，且直线DC与轴交于点Q，求点D的坐标；
(3)抛物线对称轴上是否存在一点M，使得S△MAP=2S△ACP，若存在，求出M点坐标；若不存在，请说明理由．
1题
解：（1）∵二次函数的图像经过点A（2，0）C(0,－1)
∴
解得： b=－ c=－1-------------------2分
∴二次函数的解析式为 --------3分
（2）设点D的坐标为（m，0） （0＜m＜2）
∴ OD=m ∴AD=2-m
由△ADE∽△AOC得， --------------4分
∴
∴DE=-----------------------------------5分
∴△CDE的面积=××m
== HYPERLINK "http://www./"
当m=1时，△CDE的面积最大
∴点D的坐标为（1，0）--------------------------8分
（3）存在 由(1)知：二次函数的解析式为
设y=0则 解得：x1=2 x2=－1
∴点B的坐标为（－1，0） C（0，－1）
设直线BC的解析式为：y=kx＋b
∴ 解得：k=-1 b=-1
∴直线BC的解析式为: y=－x－1
在Rt△AOC中，∠AOC=900 OA=2 OC=1
由勾股定理得：AC=
∵点B(－1,0) 点C（0，－1）
∴OB=OC ∠BCO=450
①当以点C为顶点且PC=AC=时，
设P(k, －k－1)
过点P作PH⊥y轴于H
∴∠HCP=∠BCO=450
CH=PH=∣k∣ 在Rt△PCH中
k2+k2= 解得k1=， k2=－
∴P1（，－） P2（－，）---10分
②以A为顶点，即AC=AP=
设P(k, －k－1)
过点P作PG⊥x轴于G
AG=∣2－k∣ GP=∣－k－1∣
在Rt△APG中 AG2＋PG2=AP2
（2－k)2+(－k－1)2=5
解得：k1=1,k2=0(舍)
∴P3(1, －2) ----------------------------------11分
③以P为顶点，PC=AP设P(k, －k－1)
过点P作PQ⊥y轴于点Q
PL⊥x轴于点L
∴L(k,0)
∴△QPC为等腰直角三角形
PQ=CQ=k
由勾股定理知
CP=PA=k
∴AL=∣k-2∣, PL=｜－k－1｜
在Rt△PLA中
(k)2=(k－2)2＋(k＋1)2
解得：k=∴P4(,－) ------------------------12分
综上所述： 存在四个点：P1（，－）
P2（-，） P3(1, －2) P4(,－)
2题
3题
解（1）设此抛物线的解析式为：
∵抛物线与轴交于A（1，0）、B（两点，
∴
又∵抛物线与轴交于点C（0，3）
∴，
∴
∴
即……………3分
用其他解法参照给分
（2）∵点A（1，0），点C（0，3）
∴OA=1，OC=3，
∵DC⊥AC，OC⊥轴
∴△QOC∽△COA
∴，即
∴OQ=9，……………………4分
又∵点Q在轴的负半轴上，∴Q（
设直线DC的解析式为：，则
解之得：
∴直线DC的解析式为：……………………5分
∵点D是抛物线与直线DC的交点，
∴ 解之得： （不合题意，应舍去）
∴点D（……………………6分
用其他解法参照给分
（3）如图，点M为直线上一点，连结AM，PC，PA
设点M（，直线与轴交于点E，∴AE=2
∵抛物线的顶点为P，对称轴为
∴P（
∴PE=4
则PM=
∵S四边形AEPC=S四边形OEPC+S△AOC
=
=
=……………………7分
又∵S四边形AEPC= S△AEP+S△ACP
S△AEP=
∴+S△ACP=……………………8分
∵S△MAP=2S△ACP
∴
∴
∴，……………………9分
故抛物线的对称轴上存在点M使S△MAP=2S△ACP
点M（或……………………10分
用其他解法参照给分
A
y
x
D
C
O
B
O
A
B
l
x
y
O
D
B
C
A
E
图12
第26题图
A
C
B
第26题图