2.4科学测量:用单摆测量重力加速度 同步作业-2021-2022学年高二上学期物理鲁科版(2019)选择性必修第一册(解析版)
文档属性
| 名称 | 2.4科学测量:用单摆测量重力加速度 同步作业-2021-2022学年高二上学期物理鲁科版(2019)选择性必修第一册(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-11 15:10:17 | ||
图片预览


文档简介
2021-2022学年鲁科版(2019)选择性必修第一册
2.4科学测量:用单摆测量重力加速度 同步作业(解析版)
1.某同学利用如图所示的装置测量当地的重力加速度,实验步骤如下:
A.按装置图安装好实验装置;
B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度L;
D.让小球在竖直平面内小角度摆动,当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3、…,当数到20时,停止计时,测得时间为t;
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;
G.以t2为纵坐标、L为横坐标,作出t2-L图线。
结合上述实验,完成下列问题:
(1)用游标为10分度的游标卡尺测量小球直径,某次测量示数如图所示,读出小球直径d为________cm。
(2)该同学根据实验数据,利用计算机作出t2-L图线如图所示.根据图线拟合得到方程t2=404.0L+3.07,由此可以得出当地的重力加速度g=________m/s2。(取π2=9.86,结果保留3位有效数字)
(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是_______。
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点时开始计时
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数
C.不应作t2-L图线,而应作t-L图线
D.不应作t2-L图线,而应作t2-(L+d)图线
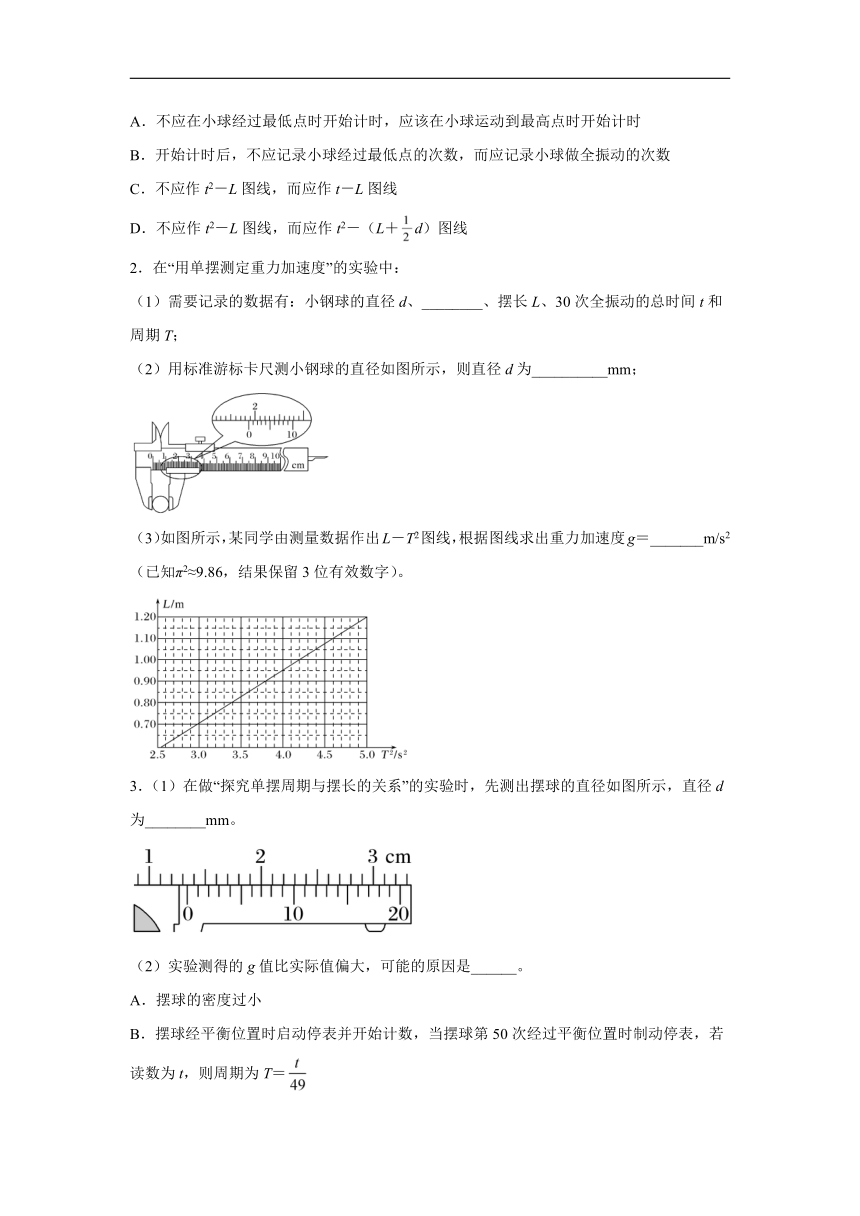
2.在“用单摆测定重力加速度”的实验中:
(1)需要记录的数据有:小钢球的直径d、________、摆长L、30次全振动的总时间t和周期T;
(2)用标准游标卡尺测小钢球的直径如图所示,则直径d为__________mm;
(3)如图所示,某同学由测量数据作出L-T2图线,根据图线求出重力加速度g=_______m/s2(已知π2≈9.86,结果保留3位有效数字)。
3.(1)在做“探究单摆周期与摆长的关系”的实验时,先测出摆球的直径如图所示,直径d为________mm。
(2)实验测得的g值比实际值偏大,可能的原因是______。
A.摆球的密度过小
B.摆球经平衡位置时启动停表并开始计数,当摆球第50次经过平衡位置时制动停表,若读数为t,则周期为T=
C.摆线上端未固定牢,摆动过程中出现松动,使摆线增长
4.某同学用单摆测定重力加速度的实验装置如图所示:
(1)对测量原理的理解正确的是________;
A.由可知,T一定时,g与L成正比
B.由可知,l一定时,g与成反比
C.单摆的振动周期T和摆长l可用实验测定,由可算出当地的重力加速度
(2)为了利用单摆较准确地测出重力加速度,应当选用以下哪些器材_______;
A.长度为左右的细绳 B.长度为左右的细绳
C.直径为的钢球 D.直径为的木球
E.最小刻度为的米尺 F.秒表、铁架台
(3)然后进行以下必要的实验操作,请将横线部分内容补充完整。
①测量单摆的摆长,即测量从摆线的悬点到_______的距离;
②把此单摆从平衡位置拉开一个小角度后释放,使摆球在竖直面内摆动,测量单摆全振动30次(或50次)的时间,求出一次全振动的时间,即单摆振动的周期;
③适当改变摆长,测量几次,并记录相应的摆长和周期;
④根据测量数据画出图像,并根据单摆的周期公式,由图像计算重力加速度。
(4)若实验得到的g值偏大,可能是因为_______;
A.组装单摆时,选择的摆球质量偏大
B.测量摆长时,将悬线长作为单摆的摆长
C.测量周期时,把n次全振动误认为是次全振动
(5)该同学利用假期分别在北京和厦门两地做了此实验,比较准确地探究了“单摆的周期T与摆长L的关系”,然后将这两组实验数据绘制了图像,如图所示,在北京测得的实验结果对应的图线是________(选填“A”、“B”)。
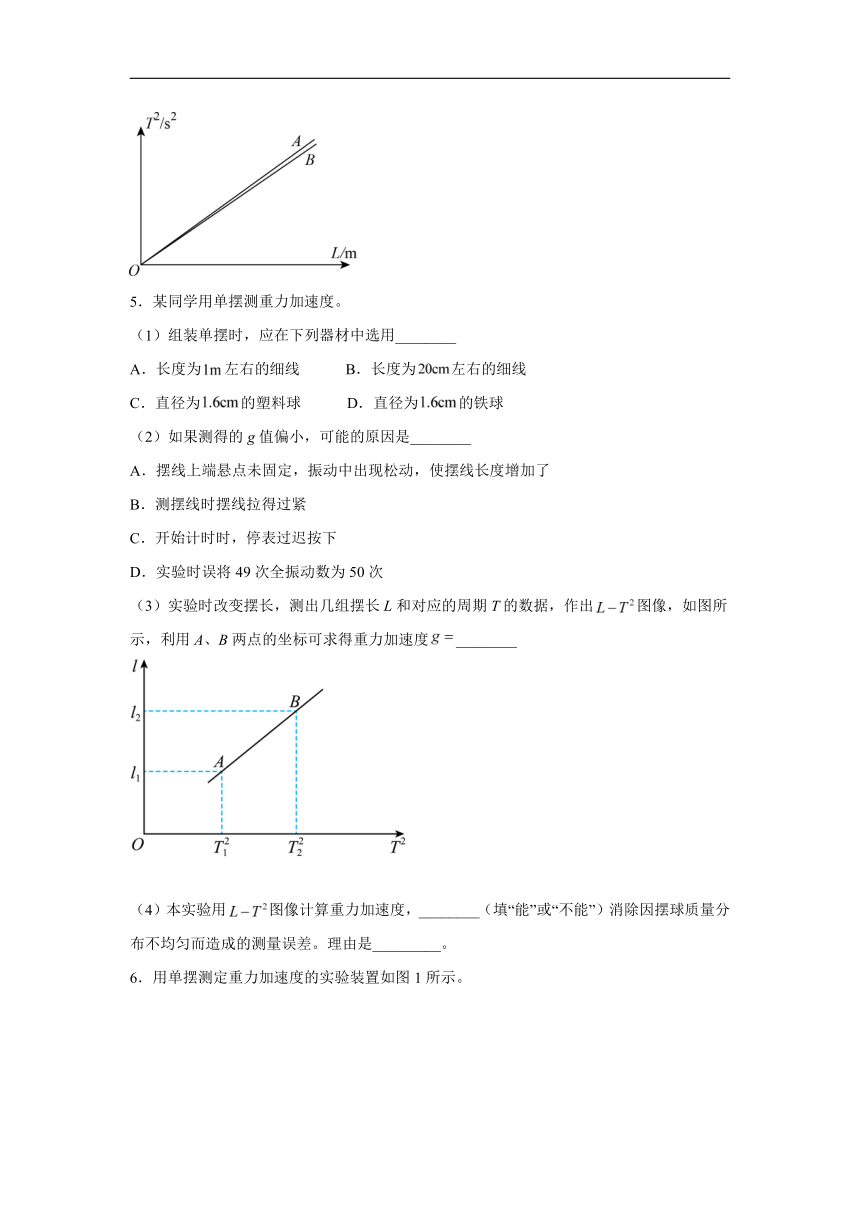
5.某同学用单摆测重力加速度。
(1)组装单摆时,应在下列器材中选用________
A.长度为左右的细线 B.长度为左右的细线
C.直径为的塑料球 D.直径为的铁球
(2)如果测得的g值偏小,可能的原因是________
A.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了
B.测摆线时摆线拉得过紧
C.开始计时时,停表过迟按下
D.实验时误将49次全振动数为50次
(3)实验时改变摆长,测出几组摆长L和对应的周期T的数据,作出图像,如图所示,利用A、B两点的坐标可求得重力加速度________
(4)本实验用图像计算重力加速度,________(填“能”或“不能”)消除因摆球质量分布不均匀而造成的测量误差。理由是_________。
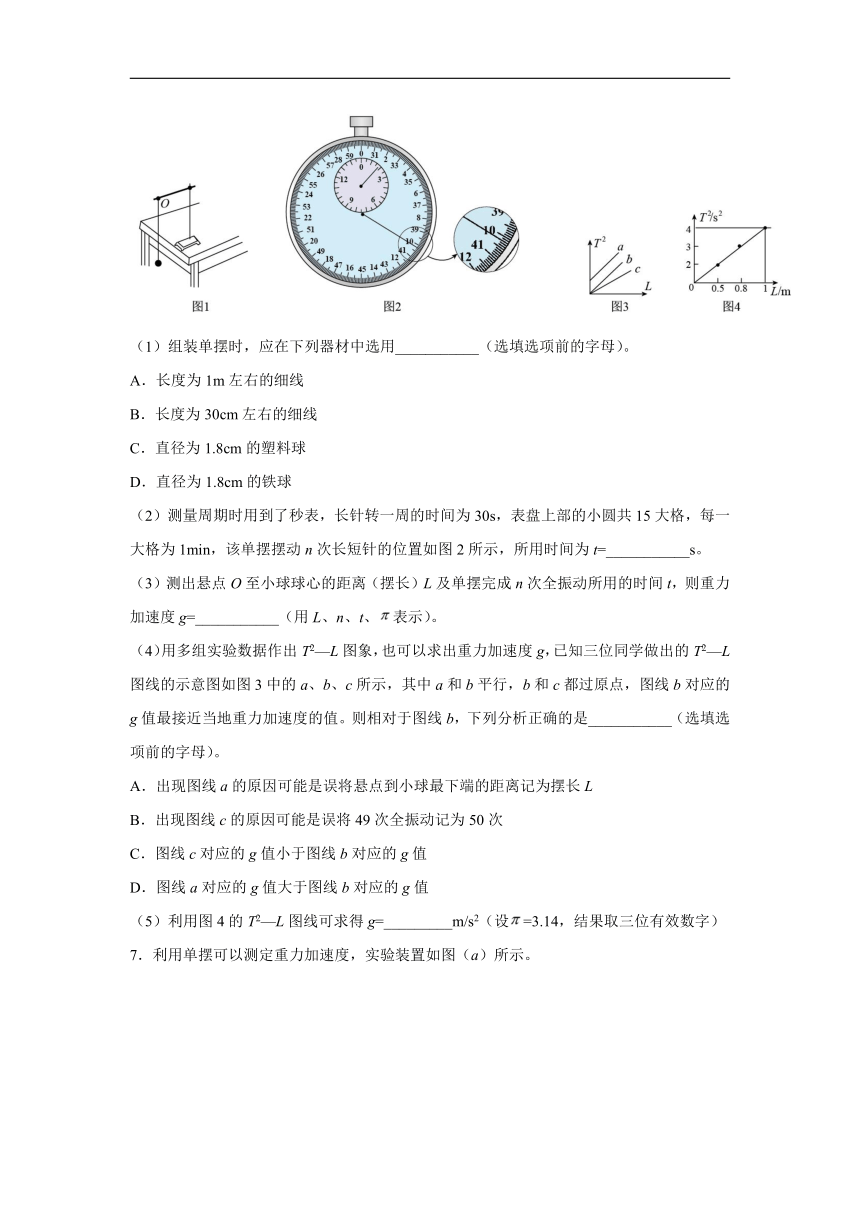
6.用单摆测定重力加速度的实验装置如图1所示。
(1)组装单摆时,应在下列器材中选用___________(选填选项前的字母)。
A.长度为1m左右的细线
B.长度为30cm左右的细线
C.直径为1.8cm的塑料球
D.直径为1.8cm的铁球
(2)测量周期时用到了秒表,长针转一周的时间为30s,表盘上部的小圆共15大格,每一大格为1min,该单摆摆动n次长短针的位置如图2所示,所用时间为t=___________s。
(3)测出悬点O至小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=___________(用L、n、t、表示)。
(4)用多组实验数据作出T2—L图象,也可以求出重力加速度g,已知三位同学做出的T2—L图线的示意图如图3中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,下列分析正确的是___________(选填选项前的字母)。
A.出现图线a的原因可能是误将悬点到小球最下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值
D.图线a对应的g值大于图线b对应的g值
(5)利用图4的T2—L图线可求得g=_________m/s2(设=3.14,结果取三位有效数字)
7.利用单摆可以测定重力加速度,实验装置如图(a)所示。
(1)利用20分度游标卡尺测定摆球的直径如图(b)所示则读数为___________;
(2)把摆球拉离平衡位置一小段位移后释放,摆球第1次经过最低点时开始计时,摆球第N次经过最低点时停止计时,测得时间为t,则单摆周期为___________;
(3)改变摆长,测出多组数据后,作出摆长l与周期平方函数关系图如图(c)所示,算出图中直线斜率为k,则当地重力加速度可表示为___________;
(4)不改变实验器材,提出一条减少实验误差的建议:___________。
8.某同学在“用单摆测定重力加速度”的实验中进行了如下的操作:
(1)用游标尺测量摆球的直径如图,可读出摆球的直径为___________。把摆球用细线悬挂在铁架台上,测量摆线长,通过计算得到摆长L。
(2)用秒表测量单摆的周期,测定了40次全振动的时间如图中秒表所示,那么秒表读数是___________s。
(3)测量出多组周期T、摆长L的数值后,画出图线,此图线斜率的物理意义是(______)
A.g B. C. D.
(4)在(3)中,描点时若误将摆线长当作摆长,那么画出的直线将不通过原点,由图线斜率得到的重力加速度与原来相比,其大小(______)
A.偏大 B.偏小 C.不变 D.都有可能
9.在做“用单摆测定重力加速度”的实验中,某同学用毫米刻度尺测得摆线长L0 = 945.8mm;用游标卡尺测得 摆球的直径如图甲所示,则摆球直径d = ______mm;用秒表测得单摆完成n = 40次全振动的时间如图乙所示,则秒表的示数t =______s;若用给定物理量符号表示当地的重力加速度g,则g = ___________。
如果该同学测得的g值偏大,可能的原因是__________。(填字母代号)
A.计算摆长时没有计入摆球的半径
B.开始计时时,秒表过迟按下
C.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
D.试验中误将39次全振动数为40次
10.在《探究单摆周期与摆长的关系》实验中:
(1)实验提供了下列器材:
A.小铁球
B.小塑料球
C.30cm长的摆线
D.100cm长的摆线
E.手表
F.秒表
G.毫米刻度尺
H.游标卡尺
I.铁架台
从上述器材中选用最合适的(填写器材代号)______;
(2)实验中用不同的仪器测得甲图所显示的数据,则甲图表示小球的直径为d=______mm,若N次全振动所花的时间为t则单摆的周期T=______;
(3)若用米尺测得的摆线长为L,结合第(2)题所给的物理量可得计算当地的重力加速度,其计算公式为g=______。
参考答案
1.1.52 9.76 D
【详解】
(1)[1]游标卡尺主尺的示数是
1.5cm=15mm
游标尺示数是
2×0.1mm=0.2mm
故小球的直径为
d=15mm+0.2mm=15.2mm=1.52cm
(2)[2]根据单摆周期公式
T=2π
得
=2π
又
l=L+
则
t2=400π2=400π2+
故t2-L图像的斜率表示的大小,由题意知斜率
k=404.0
则
=404.0
代入π2=9.86得
g≈9.76m/s2
(3)[3]A.应该在小球运动到过最低点开始计时,这样可减小由于计时位置不准确而带来的误差,故A错误;
B.记录小球经过最低点的次数,每两次为一个振动周期,不影响实验结果,故B错误;
C.根据单振的振动周期公式,就应作出t2–L图线,故C错误;
D.线长不等于摆长,摆长应是线长与半径相加,即
忽略了半径,斜率不变,不影响计算加速度,但图象不过坐标原点,故D正确。
故选D。
2.摆线长l 18.6 9.66(9.60~9.70)
【详解】
(1)[1]根据单摆的周期公式
T=2π
知要测重力加速度,需要测量小钢球的直径d、摆线长l从而得到单摆的摆长L;还要测量30次全振动的总时间t,从而得到单摆的周期T。
(2)[2]游标卡尺的主尺读数为18mm,游标尺上第6个刻度和主尺上某一刻度对齐,所以游标读数为
6×0.1mm=0.6mm
所以最终读数为
18mm+0.6mm=18.6mm
(3)[3]根据单摆的周期公式
T=2π
得
L=T2
再根据L-T2图像的斜率为
k==0.245
即
=0.245
得
g≈9.66(9.62~9.70都正确)
3.13.35 B
【详解】
(1)[1]游标卡尺主尺示数为13mm,游标尺的第7格线和主尺上刻度线对齐,游标尺示数为
7×mm=0.35mm
摆球的直径
d=(13+0.35)mm=13.35mm
(2)[2]A.根据单摆的周期公式
T=2π
可得
g=
摆球的密度过小,会使空气阻力不能忽略,测出来单摆的周期偏大,所以测出的g值比实际值偏小,故A项不符合题意;
B.摆球经平衡位置时启动停表并开始计数,当摆球第50次经过平衡位置时制动停表,若读数为t,则周期为
T=
用
T=
计算出来的周期偏小,所以测出的g值比实际值偏大,故B项符合题意;
C.摆线上端未固定牢,摆动过程中出现松动,使摆线增长,测出来的摆长偏小,所以测出的g值比实际值偏小,故C项不符合题意。
4.C BCEF 摆球球心 C B
【详解】
(1)[1] 由单摆周期公式
解得
测出单摆的摆长l与周期T,可以求出重力加速度。
故选C。
(2)[2]为减小实验误差,应选择适当长些的细绳做摆线, 摆线应选择B;为减小空气阻力对实验的影响,应选择质量大而体积小的球做摆球,因此摆球应选择C;实验需要测量摆长,需要用到刻度尺,实验需要测量单摆的周期,测周期需要秒表,应把单摆固定在铁架台上,因此需要的实验器材有:BCEF。
(3)[3] 摆线长度与摆球半径之和是单摆摆长,测量单摆的摆长,应测量从摆线的悬点到摆球球心的距离
(4)[4]根据
解得
A.单摆周期与摆球质量无关,组装单摆时,选择的摆球质量偏大不会导致g的测量值偏大,A错误;
B.测量摆长时,将悬线长作为单摆的摆长,所测摆长偏小,所测g偏小,B错误;
C.测量周期时,把n次全振动误认为是(n+1)次全振动,所测周期T偏小,所测g偏大,C正确。
故选C。
(5)[5] 根据
解得
图像的斜率
则
图像的斜率越小,重力加速度越大,由于北京的重力加速度大于厦门的重力加速度,因此在北京所做实验做出的T2-L图像的斜率小于在厦门所做实验做出的T2-L图像的斜率,由图所示图像可知,图线B的斜率小于图线A的斜率,因此在北京测得的实验结果对应的图线是B
5.AD A 能 若摆球质量不均匀,测量的摆长会不准确,但是摆长的变化量不变,图线的斜率不会发生变化。
【详解】
(1)[1]AB.单摆只能在摆角很小的情况下振动才可以看成简谐运动,为了减小误差,摆线应该选取长度为左右的细线较好,A正确,B错误;
CD.为了减小小球在摆动过程中空气阻力对实验的误差,小球应该选取直径为的铁球,C错误,D正确。
故选AD。
(2)[2]A.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了,此时摆线长度测量值小于真实值,则所测量的g值小于真实值,A正确;
B.测摆线时摆线拉得过紧,所测量的摆线长度大于真实值,所测得的g值会偏大,B错误;
C.停表过迟按下会使得周期偏小,所测得的g值偏大,C错误;
D.误将49次全振动数为50次会使得周期偏小,所测得的g值偏大,D错误。
故选A。
(3)[3]根据单摆周期公式
得
则图像斜率为
解得
(4)[4][5]若摆球质量不均匀,测量的摆长会不准确,但是摆长的变化量不变,图线的斜率不会发生变化,因此采用图像计算重力加速度能够消除因摆球质量分布不均匀而造成的测量误差。
6.AD 100.2 B 9.86
【详解】
(1)[1]AB.为了便于观察和计时,且单摆要求绳长远大于小球半径,故选择长度为1m左右的细线,A正确,B错误;
CD.为了减小空气阻力的影响,应选择密度较大的铁球,C错误,D正确。
故选AD。
(2)[2]小盘读数是90s,大盘读数是10.2s,故秒表的读数为
(3)[3]由题可知,单摆的周期为
单摆周期公式为
联立解得重力加速度为
(4)[4]根据单摆的周期公式
整理得
则图像的斜率
重力加速度
A.由图可知,图线a当L为零时T不为零,所测摆长偏小,可能是把摆线长度作为摆长,即把悬点到摆球上端的距离作为摆长,A错误;
B.实验中误将49次全振动记为50次,则周期的测量值偏小,导致重力加速度的测量值偏大,图线的斜率k偏小,B正确;
C.由图可知,图线c对应的斜率k小于图线b对应的斜率,可知图线c对应的g值大于图线b对应的g值,C错误;
D.由图可知,图线a与图线b的斜率相等,故图线a对应的g值等于图线b对应的g值,D错误。
故选B。
(5)[5]由(4)的结论,代入数据可得
解得
7.1.130 多次测量摆长和球的直径求平均值
【详解】
(1)[1] 20分度游标卡尺精确度为0.05mm,则摆球的直径为
(2)[2] 摆球第1次经过最低点时开始计时,摆球第N次经过最低点时停止计时,则通过最低点共次,而每两次通过最低点为一个周期的摆动,则单摆的周期为
(3)[3]根据单摆的周期公式,可得
故图像的斜率为
当地重力加速度可表示为
(4)[4]多次测量摆长和球的直径求平均值可减小误差。
8.2.06 75.2 C C
【详解】
(1)[1]用游标尺测量摆球的直径为2cm+0.1mm×6=2.06cm
(2)[2]秒表读数是1min+15.2s=75.2s
(3)[3]根据
可得
可知T2-L图像的斜率为,故选C。
(4)[4]在(3)中,描点时若误将摆线长当作摆长
可得
则图像的斜率不变,则由图线斜率得到的重力加速度与原来相比,其大小不变,故选C。
9.20.25 78.5 BD
【详解】
[1] 摆球直径
[2]秒表的示数
[3] 根据
其中完成一次全振动的时间
摆长
代入整理得
[4] 根据
A.若计算摆长时没有计入摆球的半径,则摆长的测量值偏小,因此重力加速度g的值偏小,A错误;
B.若开始计时时,秒表过迟按下,计算的周期偏小,从而算得的重力加速度g的值偏大,B正确;
C.若摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,而计算时按原摆长计算,相当于摆长的测量值偏小,从而算得重力加速度g的值偏小,C错误;
D.若试验中误将39次全振动数为40次,导致计算的振动周期偏小,从而算得的重力加速度g的值偏大,D正确。
故选BD。
10.ADFGHI 11.7
【详解】
(1)[1]实验中,球越重体积越小越好,故选小铁球,摆线应选相对较长点的,不能过长也不能过短,故选100cm长的细线,实验还需要测量时间,故选秒表,实验中还要知道摆长的实际长度,故需要毫米刻度尺,还要测量小铁球的直径,故需要游标卡尺,细线的另一端要固定在铁架台上,故需要铁架台;上述器材中选用最合适的是ADFGHI。
(2)[2]小球直径直径:主尺读数为1.1cm=11mm,游标尺对齐格数为7个格,读数为
70.1mm=0.7mm
所以小球直径为
d=11mm+0.7mm=11.7mm
[3]N次全振动所花的时间为t则单摆的周期为
(3)[4]由单摆周期公式
当地的重力加速度为
2.4科学测量:用单摆测量重力加速度 同步作业(解析版)
1.某同学利用如图所示的装置测量当地的重力加速度,实验步骤如下:
A.按装置图安装好实验装置;
B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度L;
D.让小球在竖直平面内小角度摆动,当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3、…,当数到20时,停止计时,测得时间为t;
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;
G.以t2为纵坐标、L为横坐标,作出t2-L图线。
结合上述实验,完成下列问题:
(1)用游标为10分度的游标卡尺测量小球直径,某次测量示数如图所示,读出小球直径d为________cm。
(2)该同学根据实验数据,利用计算机作出t2-L图线如图所示.根据图线拟合得到方程t2=404.0L+3.07,由此可以得出当地的重力加速度g=________m/s2。(取π2=9.86,结果保留3位有效数字)
(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是_______。
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点时开始计时
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数
C.不应作t2-L图线,而应作t-L图线
D.不应作t2-L图线,而应作t2-(L+d)图线
2.在“用单摆测定重力加速度”的实验中:
(1)需要记录的数据有:小钢球的直径d、________、摆长L、30次全振动的总时间t和周期T;
(2)用标准游标卡尺测小钢球的直径如图所示,则直径d为__________mm;
(3)如图所示,某同学由测量数据作出L-T2图线,根据图线求出重力加速度g=_______m/s2(已知π2≈9.86,结果保留3位有效数字)。
3.(1)在做“探究单摆周期与摆长的关系”的实验时,先测出摆球的直径如图所示,直径d为________mm。
(2)实验测得的g值比实际值偏大,可能的原因是______。
A.摆球的密度过小
B.摆球经平衡位置时启动停表并开始计数,当摆球第50次经过平衡位置时制动停表,若读数为t,则周期为T=
C.摆线上端未固定牢,摆动过程中出现松动,使摆线增长
4.某同学用单摆测定重力加速度的实验装置如图所示:
(1)对测量原理的理解正确的是________;
A.由可知,T一定时,g与L成正比
B.由可知,l一定时,g与成反比
C.单摆的振动周期T和摆长l可用实验测定,由可算出当地的重力加速度
(2)为了利用单摆较准确地测出重力加速度,应当选用以下哪些器材_______;
A.长度为左右的细绳 B.长度为左右的细绳
C.直径为的钢球 D.直径为的木球
E.最小刻度为的米尺 F.秒表、铁架台
(3)然后进行以下必要的实验操作,请将横线部分内容补充完整。
①测量单摆的摆长,即测量从摆线的悬点到_______的距离;
②把此单摆从平衡位置拉开一个小角度后释放,使摆球在竖直面内摆动,测量单摆全振动30次(或50次)的时间,求出一次全振动的时间,即单摆振动的周期;
③适当改变摆长,测量几次,并记录相应的摆长和周期;
④根据测量数据画出图像,并根据单摆的周期公式,由图像计算重力加速度。
(4)若实验得到的g值偏大,可能是因为_______;
A.组装单摆时,选择的摆球质量偏大
B.测量摆长时,将悬线长作为单摆的摆长
C.测量周期时,把n次全振动误认为是次全振动
(5)该同学利用假期分别在北京和厦门两地做了此实验,比较准确地探究了“单摆的周期T与摆长L的关系”,然后将这两组实验数据绘制了图像,如图所示,在北京测得的实验结果对应的图线是________(选填“A”、“B”)。
5.某同学用单摆测重力加速度。
(1)组装单摆时,应在下列器材中选用________
A.长度为左右的细线 B.长度为左右的细线
C.直径为的塑料球 D.直径为的铁球
(2)如果测得的g值偏小,可能的原因是________
A.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了
B.测摆线时摆线拉得过紧
C.开始计时时,停表过迟按下
D.实验时误将49次全振动数为50次
(3)实验时改变摆长,测出几组摆长L和对应的周期T的数据,作出图像,如图所示,利用A、B两点的坐标可求得重力加速度________
(4)本实验用图像计算重力加速度,________(填“能”或“不能”)消除因摆球质量分布不均匀而造成的测量误差。理由是_________。
6.用单摆测定重力加速度的实验装置如图1所示。
(1)组装单摆时,应在下列器材中选用___________(选填选项前的字母)。
A.长度为1m左右的细线
B.长度为30cm左右的细线
C.直径为1.8cm的塑料球
D.直径为1.8cm的铁球
(2)测量周期时用到了秒表,长针转一周的时间为30s,表盘上部的小圆共15大格,每一大格为1min,该单摆摆动n次长短针的位置如图2所示,所用时间为t=___________s。
(3)测出悬点O至小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=___________(用L、n、t、表示)。
(4)用多组实验数据作出T2—L图象,也可以求出重力加速度g,已知三位同学做出的T2—L图线的示意图如图3中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,下列分析正确的是___________(选填选项前的字母)。
A.出现图线a的原因可能是误将悬点到小球最下端的距离记为摆长L
B.出现图线c的原因可能是误将49次全振动记为50次
C.图线c对应的g值小于图线b对应的g值
D.图线a对应的g值大于图线b对应的g值
(5)利用图4的T2—L图线可求得g=_________m/s2(设=3.14,结果取三位有效数字)
7.利用单摆可以测定重力加速度,实验装置如图(a)所示。
(1)利用20分度游标卡尺测定摆球的直径如图(b)所示则读数为___________;
(2)把摆球拉离平衡位置一小段位移后释放,摆球第1次经过最低点时开始计时,摆球第N次经过最低点时停止计时,测得时间为t,则单摆周期为___________;
(3)改变摆长,测出多组数据后,作出摆长l与周期平方函数关系图如图(c)所示,算出图中直线斜率为k,则当地重力加速度可表示为___________;
(4)不改变实验器材,提出一条减少实验误差的建议:___________。
8.某同学在“用单摆测定重力加速度”的实验中进行了如下的操作:
(1)用游标尺测量摆球的直径如图,可读出摆球的直径为___________。把摆球用细线悬挂在铁架台上,测量摆线长,通过计算得到摆长L。
(2)用秒表测量单摆的周期,测定了40次全振动的时间如图中秒表所示,那么秒表读数是___________s。
(3)测量出多组周期T、摆长L的数值后,画出图线,此图线斜率的物理意义是(______)
A.g B. C. D.
(4)在(3)中,描点时若误将摆线长当作摆长,那么画出的直线将不通过原点,由图线斜率得到的重力加速度与原来相比,其大小(______)
A.偏大 B.偏小 C.不变 D.都有可能
9.在做“用单摆测定重力加速度”的实验中,某同学用毫米刻度尺测得摆线长L0 = 945.8mm;用游标卡尺测得 摆球的直径如图甲所示,则摆球直径d = ______mm;用秒表测得单摆完成n = 40次全振动的时间如图乙所示,则秒表的示数t =______s;若用给定物理量符号表示当地的重力加速度g,则g = ___________。
如果该同学测得的g值偏大,可能的原因是__________。(填字母代号)
A.计算摆长时没有计入摆球的半径
B.开始计时时,秒表过迟按下
C.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
D.试验中误将39次全振动数为40次
10.在《探究单摆周期与摆长的关系》实验中:
(1)实验提供了下列器材:
A.小铁球
B.小塑料球
C.30cm长的摆线
D.100cm长的摆线
E.手表
F.秒表
G.毫米刻度尺
H.游标卡尺
I.铁架台
从上述器材中选用最合适的(填写器材代号)______;
(2)实验中用不同的仪器测得甲图所显示的数据,则甲图表示小球的直径为d=______mm,若N次全振动所花的时间为t则单摆的周期T=______;
(3)若用米尺测得的摆线长为L,结合第(2)题所给的物理量可得计算当地的重力加速度,其计算公式为g=______。
参考答案
1.1.52 9.76 D
【详解】
(1)[1]游标卡尺主尺的示数是
1.5cm=15mm
游标尺示数是
2×0.1mm=0.2mm
故小球的直径为
d=15mm+0.2mm=15.2mm=1.52cm
(2)[2]根据单摆周期公式
T=2π
得
=2π
又
l=L+
则
t2=400π2=400π2+
故t2-L图像的斜率表示的大小,由题意知斜率
k=404.0
则
=404.0
代入π2=9.86得
g≈9.76m/s2
(3)[3]A.应该在小球运动到过最低点开始计时,这样可减小由于计时位置不准确而带来的误差,故A错误;
B.记录小球经过最低点的次数,每两次为一个振动周期,不影响实验结果,故B错误;
C.根据单振的振动周期公式,就应作出t2–L图线,故C错误;
D.线长不等于摆长,摆长应是线长与半径相加,即
忽略了半径,斜率不变,不影响计算加速度,但图象不过坐标原点,故D正确。
故选D。
2.摆线长l 18.6 9.66(9.60~9.70)
【详解】
(1)[1]根据单摆的周期公式
T=2π
知要测重力加速度,需要测量小钢球的直径d、摆线长l从而得到单摆的摆长L;还要测量30次全振动的总时间t,从而得到单摆的周期T。
(2)[2]游标卡尺的主尺读数为18mm,游标尺上第6个刻度和主尺上某一刻度对齐,所以游标读数为
6×0.1mm=0.6mm
所以最终读数为
18mm+0.6mm=18.6mm
(3)[3]根据单摆的周期公式
T=2π
得
L=T2
再根据L-T2图像的斜率为
k==0.245
即
=0.245
得
g≈9.66(9.62~9.70都正确)
3.13.35 B
【详解】
(1)[1]游标卡尺主尺示数为13mm,游标尺的第7格线和主尺上刻度线对齐,游标尺示数为
7×mm=0.35mm
摆球的直径
d=(13+0.35)mm=13.35mm
(2)[2]A.根据单摆的周期公式
T=2π
可得
g=
摆球的密度过小,会使空气阻力不能忽略,测出来单摆的周期偏大,所以测出的g值比实际值偏小,故A项不符合题意;
B.摆球经平衡位置时启动停表并开始计数,当摆球第50次经过平衡位置时制动停表,若读数为t,则周期为
T=
用
T=
计算出来的周期偏小,所以测出的g值比实际值偏大,故B项符合题意;
C.摆线上端未固定牢,摆动过程中出现松动,使摆线增长,测出来的摆长偏小,所以测出的g值比实际值偏小,故C项不符合题意。
4.C BCEF 摆球球心 C B
【详解】
(1)[1] 由单摆周期公式
解得
测出单摆的摆长l与周期T,可以求出重力加速度。
故选C。
(2)[2]为减小实验误差,应选择适当长些的细绳做摆线, 摆线应选择B;为减小空气阻力对实验的影响,应选择质量大而体积小的球做摆球,因此摆球应选择C;实验需要测量摆长,需要用到刻度尺,实验需要测量单摆的周期,测周期需要秒表,应把单摆固定在铁架台上,因此需要的实验器材有:BCEF。
(3)[3] 摆线长度与摆球半径之和是单摆摆长,测量单摆的摆长,应测量从摆线的悬点到摆球球心的距离
(4)[4]根据
解得
A.单摆周期与摆球质量无关,组装单摆时,选择的摆球质量偏大不会导致g的测量值偏大,A错误;
B.测量摆长时,将悬线长作为单摆的摆长,所测摆长偏小,所测g偏小,B错误;
C.测量周期时,把n次全振动误认为是(n+1)次全振动,所测周期T偏小,所测g偏大,C正确。
故选C。
(5)[5] 根据
解得
图像的斜率
则
图像的斜率越小,重力加速度越大,由于北京的重力加速度大于厦门的重力加速度,因此在北京所做实验做出的T2-L图像的斜率小于在厦门所做实验做出的T2-L图像的斜率,由图所示图像可知,图线B的斜率小于图线A的斜率,因此在北京测得的实验结果对应的图线是B
5.AD A 能 若摆球质量不均匀,测量的摆长会不准确,但是摆长的变化量不变,图线的斜率不会发生变化。
【详解】
(1)[1]AB.单摆只能在摆角很小的情况下振动才可以看成简谐运动,为了减小误差,摆线应该选取长度为左右的细线较好,A正确,B错误;
CD.为了减小小球在摆动过程中空气阻力对实验的误差,小球应该选取直径为的铁球,C错误,D正确。
故选AD。
(2)[2]A.摆线上端悬点未固定,振动中出现松动,使摆线长度增加了,此时摆线长度测量值小于真实值,则所测量的g值小于真实值,A正确;
B.测摆线时摆线拉得过紧,所测量的摆线长度大于真实值,所测得的g值会偏大,B错误;
C.停表过迟按下会使得周期偏小,所测得的g值偏大,C错误;
D.误将49次全振动数为50次会使得周期偏小,所测得的g值偏大,D错误。
故选A。
(3)[3]根据单摆周期公式
得
则图像斜率为
解得
(4)[4][5]若摆球质量不均匀,测量的摆长会不准确,但是摆长的变化量不变,图线的斜率不会发生变化,因此采用图像计算重力加速度能够消除因摆球质量分布不均匀而造成的测量误差。
6.AD 100.2 B 9.86
【详解】
(1)[1]AB.为了便于观察和计时,且单摆要求绳长远大于小球半径,故选择长度为1m左右的细线,A正确,B错误;
CD.为了减小空气阻力的影响,应选择密度较大的铁球,C错误,D正确。
故选AD。
(2)[2]小盘读数是90s,大盘读数是10.2s,故秒表的读数为
(3)[3]由题可知,单摆的周期为
单摆周期公式为
联立解得重力加速度为
(4)[4]根据单摆的周期公式
整理得
则图像的斜率
重力加速度
A.由图可知,图线a当L为零时T不为零,所测摆长偏小,可能是把摆线长度作为摆长,即把悬点到摆球上端的距离作为摆长,A错误;
B.实验中误将49次全振动记为50次,则周期的测量值偏小,导致重力加速度的测量值偏大,图线的斜率k偏小,B正确;
C.由图可知,图线c对应的斜率k小于图线b对应的斜率,可知图线c对应的g值大于图线b对应的g值,C错误;
D.由图可知,图线a与图线b的斜率相等,故图线a对应的g值等于图线b对应的g值,D错误。
故选B。
(5)[5]由(4)的结论,代入数据可得
解得
7.1.130 多次测量摆长和球的直径求平均值
【详解】
(1)[1] 20分度游标卡尺精确度为0.05mm,则摆球的直径为
(2)[2] 摆球第1次经过最低点时开始计时,摆球第N次经过最低点时停止计时,则通过最低点共次,而每两次通过最低点为一个周期的摆动,则单摆的周期为
(3)[3]根据单摆的周期公式,可得
故图像的斜率为
当地重力加速度可表示为
(4)[4]多次测量摆长和球的直径求平均值可减小误差。
8.2.06 75.2 C C
【详解】
(1)[1]用游标尺测量摆球的直径为2cm+0.1mm×6=2.06cm
(2)[2]秒表读数是1min+15.2s=75.2s
(3)[3]根据
可得
可知T2-L图像的斜率为,故选C。
(4)[4]在(3)中,描点时若误将摆线长当作摆长
可得
则图像的斜率不变,则由图线斜率得到的重力加速度与原来相比,其大小不变,故选C。
9.20.25 78.5 BD
【详解】
[1] 摆球直径
[2]秒表的示数
[3] 根据
其中完成一次全振动的时间
摆长
代入整理得
[4] 根据
A.若计算摆长时没有计入摆球的半径,则摆长的测量值偏小,因此重力加速度g的值偏小,A错误;
B.若开始计时时,秒表过迟按下,计算的周期偏小,从而算得的重力加速度g的值偏大,B正确;
C.若摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,而计算时按原摆长计算,相当于摆长的测量值偏小,从而算得重力加速度g的值偏小,C错误;
D.若试验中误将39次全振动数为40次,导致计算的振动周期偏小,从而算得的重力加速度g的值偏大,D正确。
故选BD。
10.ADFGHI 11.7
【详解】
(1)[1]实验中,球越重体积越小越好,故选小铁球,摆线应选相对较长点的,不能过长也不能过短,故选100cm长的细线,实验还需要测量时间,故选秒表,实验中还要知道摆长的实际长度,故需要毫米刻度尺,还要测量小铁球的直径,故需要游标卡尺,细线的另一端要固定在铁架台上,故需要铁架台;上述器材中选用最合适的是ADFGHI。
(2)[2]小球直径直径:主尺读数为1.1cm=11mm,游标尺对齐格数为7个格,读数为
70.1mm=0.7mm
所以小球直径为
d=11mm+0.7mm=11.7mm
[3]N次全振动所花的时间为t则单摆的周期为
(3)[4]由单摆周期公式
当地的重力加速度为
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
