人教版数学八年 级上册14.3.2公式法---平方差公式【教案】
文档属性
| 名称 | 人教版数学八年 级上册14.3.2公式法---平方差公式【教案】 |
|
|
| 格式 | zip | ||
| 文件大小 | 92.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览

文档简介
完全平方公式
教学目标:
(1)、知识与技能:1.完全平方公式的推导及其应用.2.能运用完全平方公式进行简单的运算.3.完全平方公式的几何解释。
(2)、过程与方法:1.经历探索完全平方公式的过程,进一步发展符号感和推理能力.2.有意识地培养学生的思维条理性和表达能力。
(3)、情感、态度与价值观:在灵活应用公式的过程中激发学生学习数学的兴趣,培养创新能力和探索精神.体会数形结合的思想。
教学重点:完全平方公式的结构特征及运用。
教学难点:对具体问题会运用公式以及理解公式中字母的广泛含义。
教具准备:多媒体课件等。
教学过程设计:
一、【活动1】:
回顾与思考:1、请你叙述平方差公式并用字母表示。2、公式的结构特征及运用平方差公式的注意事项。
二、【活动2】:交流合作、探索发现
本次活动,通过创设问题情境,让学生尝试用两种不同的方法表示试验田的总面积,从而得到等式:
(a+b)?=a?+2ab+b?
。
问题:一块边长为a米的正方形实验田,因需要将其边长增加
b
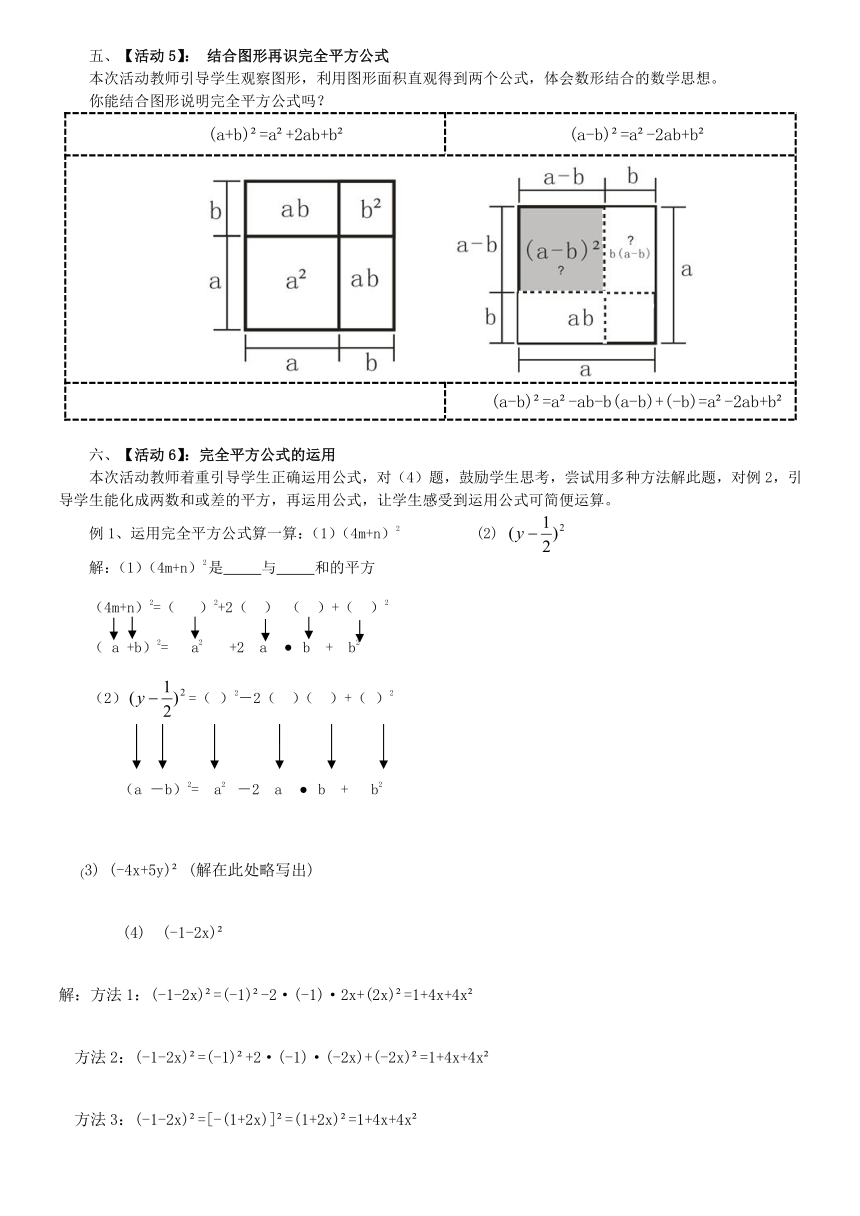
米。形成四块实验田,以种植不同的新品种(如图1—6).用不同的形式表示实验田的总面积,
并进行比较.
探索:
你发现了什么?
图1—6
方法一:总面积=(a+b)?
方法二:总面积=a?+ab+ab+b?
=a?+2ab+b?
结论:(a+b)?=a?+2ab+b?
3、【活动3】:验证并揭示完全平方公式
本次活动着重引导学生利用多项式的乘法法则说明(a+b)?=a?+2ab+b?成立,然后由此等式直接导出(a-b)?=a?-2ab+b?,揭示完全平方公式:(a+b)?=a?+2ab+b?(a-b)?=a?-2ab+b?
(1)、你能用多项式的乘法法则来说明它成立吗?
(2)、小明写出了如下的算式:(a-b)?=[a+(-b)]?他是怎么想的?你能继续做下去吗?
推证:(a+b)?=(a+b)(a+b)=a?+ab+ab+b?=a?+2ab+b?
(a-b)?=[a+(-b)]?=a?+2a(-b)+(-b)?=a?-2ab+b?
4、【活动4】:
初识完全平方公式
引导学生观察公式,说出公式的结构特征,理解公式中字母的含义。
完全平方公式:(a+b)?=a?+2ab+b?(a-b)?=a?-2ab+b?
结构特征:1、左边:二项式:两数和(差)的平方。2、右边:二次三项式:首末是两数的平方和,中间是这两项积的两倍,符号与前面相同。3、公式中的字母a,b可以表示单项式或多项式。
5、【活动5】:
结合图形再识完全平方公式
本次活动教师引导学生观察图形,利用图形面积直观得到两个公式,体会数形结合的数学思想。
你能结合图形说明完全平方公式吗?
(a+b)?=a?+2ab+b?
(a-b)?=a?-2ab+b?
(a-b)?=a?-ab-b(a-b)+(-b)=a?-2ab+b?
6、【活动6】:完全平方公式的运用
本次活动教师着重引导学生正确运用公式,对(4)题,鼓励学生思考,尝试用多种方法解此题,对例2,引导学生能化成两数和或差的平方,再运用公式,让学生感受到运用公式可简便运算。
例1、运用完全平方公式算一算:(1)(4m+n)2
(2)
解:(1)(4m+n)2是
与
和的平方
(4m+n)2=(
)2+2(
)
(
)+(
)2
(
a
+b)2=
a2
+2
a
b
+ b2
(2)=(
)2-2(
)(
)+(
)2
(a
-b)2=
a2
-2
a
b
+
b2
(3)
(-4x+5y)?
(解在此处略写出)
(4)
(-1-2x)?
解:方法1:(-1-2x)?=(-1)?-2·(-1)·2x+(2x)?=1+4x+4x?
方法2:(-1-2x)?=(-1)?+2·(-1)·(-2x)+(-2x)?=1+4x+4x?
方法3:(-1-2x)?=[-(1+2x)]?=(1+2x)?=1+4x+4x?
例2、
利用完全平方公式计算:
(1)102?
(2)99?
解:(1)102?=(100+2)
?=100?+2×100×2+2?=10000+400+4=10404
(2)
99?=(100-1)?=100?-2×100×1+1?=10000-200+1=9801
7、【活动7】
大胆尝试
练一练
本次活动,学生尝试运用完全平方公式独立完成计算,教师重点关注学生计算的准确性、熟练性、灵活性。注意学生信息的反馈,及时纠错。
1.利用完全平方公式计算:
(1)
(x
+6)?
(2)
(y-5)?
(3)
(-2x+5
)?
(4)
(3/4x-2/3y)?
(5)(-n
-1)?
?n?
(6)99.8?
2、纠错练习、
改一改.
指出下列各式中的错误,并加以改正:
(1)
(2a?1)?=2a??2a+1
(2)
(2a+1)?=4a?
+1
(3)
(a?1)?=a??2a?1
(4)
(a+b)?=a?+b?
(5)(a-b)?=a?-b?
解:
(1)第一数被平方时,
未添括号;第一数与第二数乘积的2倍少乘了一个2
;应改为:
(2a?1)2=
(2a)2?2?
2a?1+1。
(2)
少了第一数与第二数乘积的2倍
(丢了一项);应改为:
(2a+1)?=
(2a)?+2?2a?1
+1。
(3)
第一数平方未添括号,
第一数与第二数乘积的2倍
错了符号;第二数的平方
这一项错了符号;应改为:
(a?1)?=(a)?2?a
?1+12。
3、巩固练习
、选一选
:1)、下列计算中,正确的是(
)
A.
(a+b)?=a?+b?
B.
(a+2b)(-2b-a)=a?-4b?
C.
(a-2b)?=a?-4b+2b?
D.
(x+3y)
?=x?+6xy+9y?
2)、(x-y)?(x+y)?的计算结果是(
)项
A.
一项
B.
二项
C.
三项
D.
四项
3)、下列各式的计算,正确式子的个数是(
)
(1)(2x-6y)?=4x?-12xy+36y?
(2).(x+6)(x-6)=x?-6
(3).
(-x-2y)?=x?-4xy+4y?
(4).(a+2b)=a?+4ab+4b?
A.1
B.2
C.3
D.4
4、拓展思维
举一反三:
1)、(x-y)(x+y)(x?-y?)
2)、(x-y)?-(2x+y)(y-2x)
3)、(x+1)?(x?+1)
?(x-1)?
4)、(a+b+c)?
5)、(2x-y-3)?
6)、若4x?+kxy+9y?是完全平方式,则k=___
八、【活动8
】
1、
课堂小结:
本节课你学到了什么知识?有什么认识?
1).
注意完全平方公式和平方差公式不同:
形式不同:
结果不同:完全平方公式的结果是三项,即
(a±b)?=a?±2ab+b?;平方差公式的结果是两项,即
(a+b)(a?b)=a??b?.
2).
在解题过程中要准确确定a和b,对照公式原形的两边,
做到不丢项、不弄错符号、2ab时不少乘2。
3).
口诀:首平方,尾平方,两倍乘积放中央,加减看前方,同加异减莫弄反。
2、布置作业:
1).
基础训练:教材习题第2.3.4题
2).
拓展练习:
公式的拓展:在(a±b)
?=a?±2ab+b?中,若a+b,a-b,a?+b?,
ab等四个代数之间存在如下关系:
(1)
a?+b?=(a+b)
?-
2ab
a?+b?=(a-b)
?+2ab
(2)(a+b)?=(a-b)
?-
-4ab
(a-b)?=(a+b)
?+-4ab
(3)
已知a+b=-3
ab=2
求下列各式的值
(1)
a?+b?
(2)a?-ab+b?
(3)(a-b)?
教学目标:
(1)、知识与技能:1.完全平方公式的推导及其应用.2.能运用完全平方公式进行简单的运算.3.完全平方公式的几何解释。
(2)、过程与方法:1.经历探索完全平方公式的过程,进一步发展符号感和推理能力.2.有意识地培养学生的思维条理性和表达能力。
(3)、情感、态度与价值观:在灵活应用公式的过程中激发学生学习数学的兴趣,培养创新能力和探索精神.体会数形结合的思想。
教学重点:完全平方公式的结构特征及运用。
教学难点:对具体问题会运用公式以及理解公式中字母的广泛含义。
教具准备:多媒体课件等。
教学过程设计:
一、【活动1】:
回顾与思考:1、请你叙述平方差公式并用字母表示。2、公式的结构特征及运用平方差公式的注意事项。
二、【活动2】:交流合作、探索发现
本次活动,通过创设问题情境,让学生尝试用两种不同的方法表示试验田的总面积,从而得到等式:
(a+b)?=a?+2ab+b?
。
问题:一块边长为a米的正方形实验田,因需要将其边长增加
b
米。形成四块实验田,以种植不同的新品种(如图1—6).用不同的形式表示实验田的总面积,
并进行比较.
探索:
你发现了什么?
图1—6
方法一:总面积=(a+b)?
方法二:总面积=a?+ab+ab+b?
=a?+2ab+b?
结论:(a+b)?=a?+2ab+b?
3、【活动3】:验证并揭示完全平方公式
本次活动着重引导学生利用多项式的乘法法则说明(a+b)?=a?+2ab+b?成立,然后由此等式直接导出(a-b)?=a?-2ab+b?,揭示完全平方公式:(a+b)?=a?+2ab+b?(a-b)?=a?-2ab+b?
(1)、你能用多项式的乘法法则来说明它成立吗?
(2)、小明写出了如下的算式:(a-b)?=[a+(-b)]?他是怎么想的?你能继续做下去吗?
推证:(a+b)?=(a+b)(a+b)=a?+ab+ab+b?=a?+2ab+b?
(a-b)?=[a+(-b)]?=a?+2a(-b)+(-b)?=a?-2ab+b?
4、【活动4】:
初识完全平方公式
引导学生观察公式,说出公式的结构特征,理解公式中字母的含义。
完全平方公式:(a+b)?=a?+2ab+b?(a-b)?=a?-2ab+b?
结构特征:1、左边:二项式:两数和(差)的平方。2、右边:二次三项式:首末是两数的平方和,中间是这两项积的两倍,符号与前面相同。3、公式中的字母a,b可以表示单项式或多项式。
5、【活动5】:
结合图形再识完全平方公式
本次活动教师引导学生观察图形,利用图形面积直观得到两个公式,体会数形结合的数学思想。
你能结合图形说明完全平方公式吗?
(a+b)?=a?+2ab+b?
(a-b)?=a?-2ab+b?
(a-b)?=a?-ab-b(a-b)+(-b)=a?-2ab+b?
6、【活动6】:完全平方公式的运用
本次活动教师着重引导学生正确运用公式,对(4)题,鼓励学生思考,尝试用多种方法解此题,对例2,引导学生能化成两数和或差的平方,再运用公式,让学生感受到运用公式可简便运算。
例1、运用完全平方公式算一算:(1)(4m+n)2
(2)
解:(1)(4m+n)2是
与
和的平方
(4m+n)2=(
)2+2(
)
(
)+(
)2
(
a
+b)2=
a2
+2
a
b
+ b2
(2)=(
)2-2(
)(
)+(
)2
(a
-b)2=
a2
-2
a
b
+
b2
(3)
(-4x+5y)?
(解在此处略写出)
(4)
(-1-2x)?
解:方法1:(-1-2x)?=(-1)?-2·(-1)·2x+(2x)?=1+4x+4x?
方法2:(-1-2x)?=(-1)?+2·(-1)·(-2x)+(-2x)?=1+4x+4x?
方法3:(-1-2x)?=[-(1+2x)]?=(1+2x)?=1+4x+4x?
例2、
利用完全平方公式计算:
(1)102?
(2)99?
解:(1)102?=(100+2)
?=100?+2×100×2+2?=10000+400+4=10404
(2)
99?=(100-1)?=100?-2×100×1+1?=10000-200+1=9801
7、【活动7】
大胆尝试
练一练
本次活动,学生尝试运用完全平方公式独立完成计算,教师重点关注学生计算的准确性、熟练性、灵活性。注意学生信息的反馈,及时纠错。
1.利用完全平方公式计算:
(1)
(x
+6)?
(2)
(y-5)?
(3)
(-2x+5
)?
(4)
(3/4x-2/3y)?
(5)(-n
-1)?
?n?
(6)99.8?
2、纠错练习、
改一改.
指出下列各式中的错误,并加以改正:
(1)
(2a?1)?=2a??2a+1
(2)
(2a+1)?=4a?
+1
(3)
(a?1)?=a??2a?1
(4)
(a+b)?=a?+b?
(5)(a-b)?=a?-b?
解:
(1)第一数被平方时,
未添括号;第一数与第二数乘积的2倍少乘了一个2
;应改为:
(2a?1)2=
(2a)2?2?
2a?1+1。
(2)
少了第一数与第二数乘积的2倍
(丢了一项);应改为:
(2a+1)?=
(2a)?+2?2a?1
+1。
(3)
第一数平方未添括号,
第一数与第二数乘积的2倍
错了符号;第二数的平方
这一项错了符号;应改为:
(a?1)?=(a)?2?a
?1+12。
3、巩固练习
、选一选
:1)、下列计算中,正确的是(
)
A.
(a+b)?=a?+b?
B.
(a+2b)(-2b-a)=a?-4b?
C.
(a-2b)?=a?-4b+2b?
D.
(x+3y)
?=x?+6xy+9y?
2)、(x-y)?(x+y)?的计算结果是(
)项
A.
一项
B.
二项
C.
三项
D.
四项
3)、下列各式的计算,正确式子的个数是(
)
(1)(2x-6y)?=4x?-12xy+36y?
(2).(x+6)(x-6)=x?-6
(3).
(-x-2y)?=x?-4xy+4y?
(4).(a+2b)=a?+4ab+4b?
A.1
B.2
C.3
D.4
4、拓展思维
举一反三:
1)、(x-y)(x+y)(x?-y?)
2)、(x-y)?-(2x+y)(y-2x)
3)、(x+1)?(x?+1)
?(x-1)?
4)、(a+b+c)?
5)、(2x-y-3)?
6)、若4x?+kxy+9y?是完全平方式,则k=___
八、【活动8
】
1、
课堂小结:
本节课你学到了什么知识?有什么认识?
1).
注意完全平方公式和平方差公式不同:
形式不同:
结果不同:完全平方公式的结果是三项,即
(a±b)?=a?±2ab+b?;平方差公式的结果是两项,即
(a+b)(a?b)=a??b?.
2).
在解题过程中要准确确定a和b,对照公式原形的两边,
做到不丢项、不弄错符号、2ab时不少乘2。
3).
口诀:首平方,尾平方,两倍乘积放中央,加减看前方,同加异减莫弄反。
2、布置作业:
1).
基础训练:教材习题第2.3.4题
2).
拓展练习:
公式的拓展:在(a±b)
?=a?±2ab+b?中,若a+b,a-b,a?+b?,
ab等四个代数之间存在如下关系:
(1)
a?+b?=(a+b)
?-
2ab
a?+b?=(a-b)
?+2ab
(2)(a+b)?=(a-b)
?-
-4ab
(a-b)?=(a+b)
?+-4ab
(3)
已知a+b=-3
ab=2
求下列各式的值
(1)
a?+b?
(2)a?-ab+b?
(3)(a-b)?
