人教版八年级上册 12.3角的平分线的性质 教案
文档属性
| 名称 | 人教版八年级上册 12.3角的平分线的性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 178.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 10:04:38 | ||
图片预览


文档简介
课程基本信息
课题
角的平分线的性质(3)
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:2013年
6月
教学目标
教学目标:1.学习并使用新的定理——角的内部到角的两边的距离相等的点在角的平分线上;
2.通过探究定理及应用定理的过程,进一步提高学生的逻辑推理能力.
教学重点:掌握新的定理的内容、证明,注意其与角的平分线的性质的区别和联系,并会进行推理与书写.
教学难点:准确运用新定理综合解决相关几何问题.
教学过程
时间
教学环节
主要师生活动
1分钟
3分钟
2-3分钟
3-4分钟
4-5分钟
4-5分钟
5-6分钟
1-2分钟
知识回顾
定理及证明
例题讲解
小结与作业
知识回顾
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
题设:一个点在一个角的平分线上.
结论:它到角的两边的距离相等.
问题
交换角的平分线的性质中的题设和结论,你能得到什么命题?这个新命题正确吗?我们用之前用过的图配合具体例题来看一下.
已知:如图,PD⊥OA,PE⊥OB,PD
=
PE.
求证:点P在∠AOB的平分线上(AP平分∠AOB).
证明:∵
PD⊥OA,PE⊥OB(已知),
∴
∠PDO=∠PEO=90°(垂直的定义).
在Rt△PDO和Rt△PEO中,
∴
Rt△PDO≌Rt△PEO(HL).
∴
∠POD=∠POE.
∴点P在∠AOB的平分线上.
结论(这是在角的平分线的性质一节出现的第2个定理)
角的内部到角的两边的距离相等的点在角的平分线上.
即,单纯交换角的平分线的性质中的题设与结论,所得到的结论有问题.
留一个思考问题:为什么会有“角的内部”这个前提?没有的话会怎样?
我们将在下节课来回答这个问题.
使用这个定理时这样书写:
∵
PD⊥OA,PE⊥OB,PD=PE,
∴点P在∠AOB的平分线上.
“双垂距等推角分”
例1
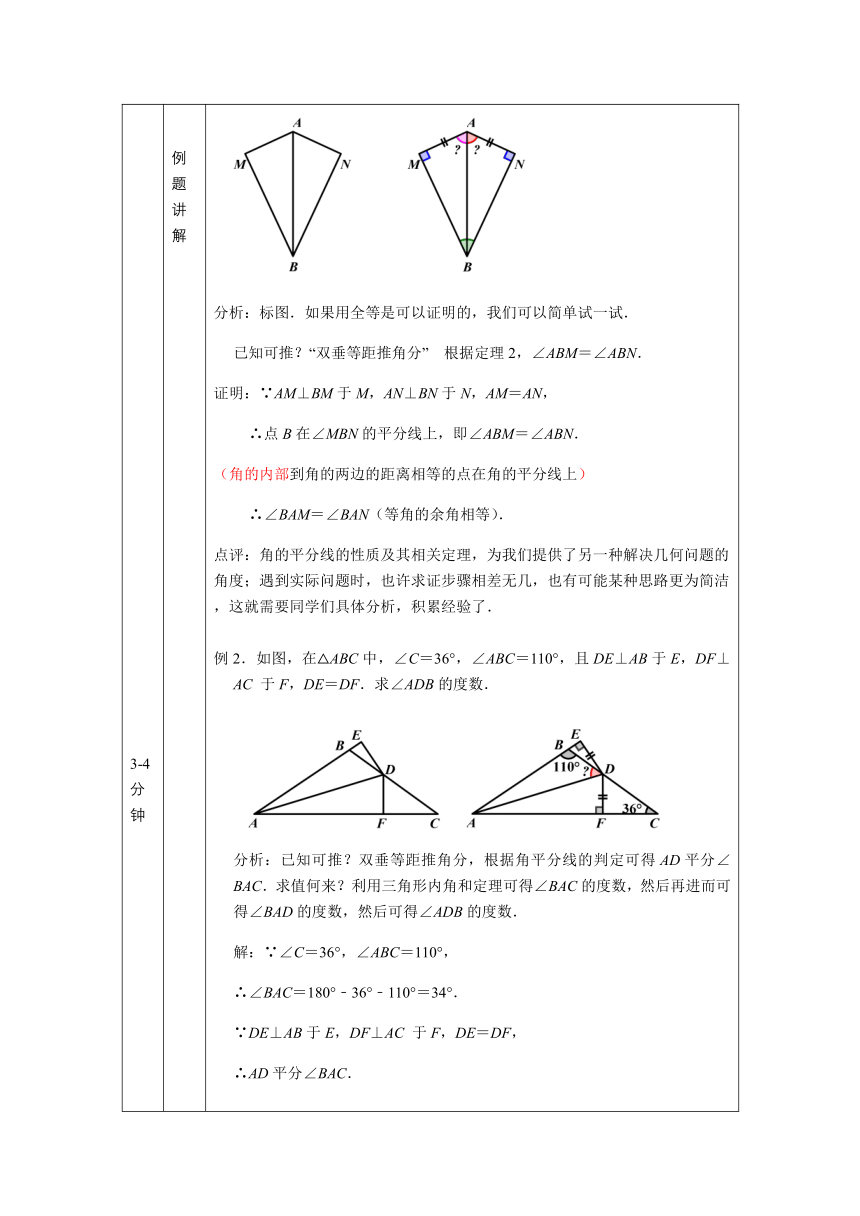
如图所示,AM⊥BM于M,AN⊥BN于N,AM=AN,求证:∠BAM=∠BAN(要求不用全等的知识证明).
分析:标图.如果用全等是可以证明的,我们可以简单试一试.
已知可推?“双垂等距推角分”
根据定理2,∠ABM=∠ABN.
证明:∵AM⊥BM于M,AN⊥BN于N,AM=AN,
∴点B在∠MBN的平分线上,即∠ABM=∠ABN.
(角的内部到角的两边的距离相等的点在角的平分线上)
∴∠BAM=∠BAN(等角的余角相等).
点评:角的平分线的性质及其相关定理,为我们提供了另一种解决几何问题的角度;遇到实际问题时,也许求证步骤相差无几,也有可能某种思路更为简洁,这就需要同学们具体分析,积累经验了.
例2.如图,在△ABC中,∠C=36°,∠ABC=110°,且DE⊥AB于E,DF⊥AC
于F,DE=DF.求∠ADB的度数.
分析:已知可推?双垂等距推角分,根据角平分线的判定可得AD平分∠BAC.求值何来?利用三角形内角和定理可得∠BAC的度数,然后再进而可得∠BAD的度数,然后可得∠ADB的度数.
解:∵∠C=36°,∠ABC=110°,
∴∠BAC=180°﹣36°﹣110°=34°.
∵DE⊥AB于E,DF⊥AC
于F,DE=DF,
∴AD平分∠BAC.
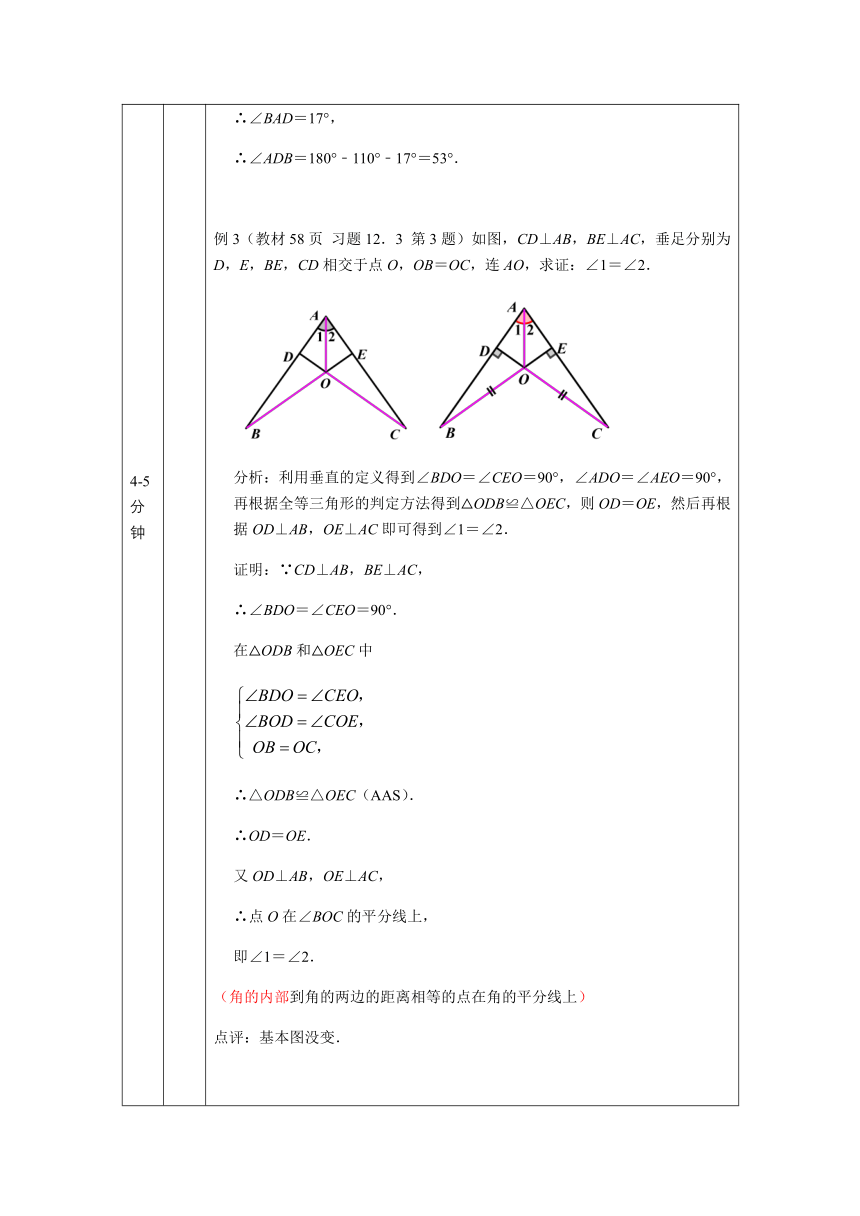
∴∠BAD=17°,
∴∠ADB=180°﹣110°﹣17°=53°.
例3(教材58页
习题12.3
第3题)如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,连AO,求证:∠1=∠2.
分析:利用垂直的定义得到∠BDO=∠CEO=90°,∠ADO=∠AEO=90°,再根据全等三角形的判定方法得到△ODB≌△OEC,则OD=OE,然后再根据OD⊥AB,OE⊥AC即可得到∠1=∠2.
证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°.
在△ODB和△OEC中
∴△ODB≌△OEC(AAS).
∴OD=OE.
又OD⊥AB,OE⊥AC,
∴点O在∠BOC的平分线上,
即∠1=∠2.
(角的内部到角的两边的距离相等的点在角的平分线上)
点评:基本图没变.
例4.如图,D,E,F分别是△ABC的三条边上的点,BE=CF,△DBE和△DCF的面积相等.求证:AD平分∠BAC.
分析:标图
已知可推?直接用面积要找底高,考虑作垂直,面积和一边等,则高等.
求证何来?“双垂等距推角分”
过D作DM⊥AB于M,DN⊥AC于N,根据条件“△DBE和△DCF的面积相等”,分别表示出△DBE和△DCF的面积,可得到BE?DM=CF?DN;由于BE=CF,可得结论DM=DN;根据新学的定理,进而得到AD平分∠BAC.
证明:过D作DM⊥AB于M,DN⊥AC于N.
∵△DBE和△DCF的面积相等,
∴BE?DM=CF?DN.
又∵BE=CF,
∴DM=DN.
又∵DM⊥AB,DN⊥AC,
∴AD平分∠BAC(在角的内部,到角两边距离相等的点在角的平分线上).
点评:基本辅助线没变.
例5.如图,OP为∠AOB内一条射线,C,D分别为OA,OB上两点,且∠PCO+∠PDO=180°,PC=PD.求证:OP平分∠AOB.
分析:标图
已知可推?邻补角好找180?,可以转换为等角的条件
求证何来?“双垂等距推角分”
作双垂,欠等距,全等推
整理一下思路:
1.作双垂
2.由180?找等角,供全等用
3.证明两三角形全等
4.得距离等,配双垂证角等
证明:过点P作PM⊥OA,PN⊥OB.
则∠PMC=∠PND=90°
∵∠PCO+∠PDO=180°,
∠PCO+∠PCM=180°,
∴∠PCM=∠PDN.
在△PMC与△PND中
∴△PMC≌△PND.
∴PM=PN.
∵PM⊥OA,PN⊥OB,
∴OP平分∠AOB.
小结今天的学习内容
新的定理:在角的内部,到角的两边的距离相等的点在角的平分线上.
新的应用:“双垂距离推角分”
.
务必关注到目前学过的两个定理的异同.(基本图不变,辅助线不变)
课后作业
1.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ).
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
分析:过两把直尺的交点C作CE⊥AO,CF⊥BO,根据题意可得CE=CF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB;
解:(1)如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO.
又∵两把完全相同的长方形直尺,
∴PE=PF.
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上).
故选:A.
2.如图所示,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E,F,且BE=CF,求证:AD是△ABC的角平分线.
分析:首先可证明Rt△BDE≌Rt△DCF(HL),再根据定理2,求得AD是△ABC的角平分线即可.
证明:∵DE⊥AB,DF⊥AC,
∴在Rt△BDE与Rt△DCF中.
∴Rt△BDE≌Rt△DCF(HL).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
备用题
练习
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
分析:根据全等三角形的判定定理得出Rt△BDE≌Rt△CDF,进而得出DE=DF,由定理2可知AD是∠BAC的平分线.
证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
在Rt△BDE与Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴AD是∠BAC的平分线.
课题
角的平分线的性质(3)
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:2013年
6月
教学目标
教学目标:1.学习并使用新的定理——角的内部到角的两边的距离相等的点在角的平分线上;
2.通过探究定理及应用定理的过程,进一步提高学生的逻辑推理能力.
教学重点:掌握新的定理的内容、证明,注意其与角的平分线的性质的区别和联系,并会进行推理与书写.
教学难点:准确运用新定理综合解决相关几何问题.
教学过程
时间
教学环节
主要师生活动
1分钟
3分钟
2-3分钟
3-4分钟
4-5分钟
4-5分钟
5-6分钟
1-2分钟
知识回顾
定理及证明
例题讲解
小结与作业
知识回顾
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
题设:一个点在一个角的平分线上.
结论:它到角的两边的距离相等.
问题
交换角的平分线的性质中的题设和结论,你能得到什么命题?这个新命题正确吗?我们用之前用过的图配合具体例题来看一下.
已知:如图,PD⊥OA,PE⊥OB,PD
=
PE.
求证:点P在∠AOB的平分线上(AP平分∠AOB).
证明:∵
PD⊥OA,PE⊥OB(已知),
∴
∠PDO=∠PEO=90°(垂直的定义).
在Rt△PDO和Rt△PEO中,
∴
Rt△PDO≌Rt△PEO(HL).
∴
∠POD=∠POE.
∴点P在∠AOB的平分线上.
结论(这是在角的平分线的性质一节出现的第2个定理)
角的内部到角的两边的距离相等的点在角的平分线上.
即,单纯交换角的平分线的性质中的题设与结论,所得到的结论有问题.
留一个思考问题:为什么会有“角的内部”这个前提?没有的话会怎样?
我们将在下节课来回答这个问题.
使用这个定理时这样书写:
∵
PD⊥OA,PE⊥OB,PD=PE,
∴点P在∠AOB的平分线上.
“双垂距等推角分”
例1
如图所示,AM⊥BM于M,AN⊥BN于N,AM=AN,求证:∠BAM=∠BAN(要求不用全等的知识证明).
分析:标图.如果用全等是可以证明的,我们可以简单试一试.
已知可推?“双垂等距推角分”
根据定理2,∠ABM=∠ABN.
证明:∵AM⊥BM于M,AN⊥BN于N,AM=AN,
∴点B在∠MBN的平分线上,即∠ABM=∠ABN.
(角的内部到角的两边的距离相等的点在角的平分线上)
∴∠BAM=∠BAN(等角的余角相等).
点评:角的平分线的性质及其相关定理,为我们提供了另一种解决几何问题的角度;遇到实际问题时,也许求证步骤相差无几,也有可能某种思路更为简洁,这就需要同学们具体分析,积累经验了.
例2.如图,在△ABC中,∠C=36°,∠ABC=110°,且DE⊥AB于E,DF⊥AC
于F,DE=DF.求∠ADB的度数.
分析:已知可推?双垂等距推角分,根据角平分线的判定可得AD平分∠BAC.求值何来?利用三角形内角和定理可得∠BAC的度数,然后再进而可得∠BAD的度数,然后可得∠ADB的度数.
解:∵∠C=36°,∠ABC=110°,
∴∠BAC=180°﹣36°﹣110°=34°.
∵DE⊥AB于E,DF⊥AC
于F,DE=DF,
∴AD平分∠BAC.
∴∠BAD=17°,
∴∠ADB=180°﹣110°﹣17°=53°.
例3(教材58页
习题12.3
第3题)如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,连AO,求证:∠1=∠2.
分析:利用垂直的定义得到∠BDO=∠CEO=90°,∠ADO=∠AEO=90°,再根据全等三角形的判定方法得到△ODB≌△OEC,则OD=OE,然后再根据OD⊥AB,OE⊥AC即可得到∠1=∠2.
证明:∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°.
在△ODB和△OEC中
∴△ODB≌△OEC(AAS).
∴OD=OE.
又OD⊥AB,OE⊥AC,
∴点O在∠BOC的平分线上,
即∠1=∠2.
(角的内部到角的两边的距离相等的点在角的平分线上)
点评:基本图没变.
例4.如图,D,E,F分别是△ABC的三条边上的点,BE=CF,△DBE和△DCF的面积相等.求证:AD平分∠BAC.
分析:标图
已知可推?直接用面积要找底高,考虑作垂直,面积和一边等,则高等.
求证何来?“双垂等距推角分”
过D作DM⊥AB于M,DN⊥AC于N,根据条件“△DBE和△DCF的面积相等”,分别表示出△DBE和△DCF的面积,可得到BE?DM=CF?DN;由于BE=CF,可得结论DM=DN;根据新学的定理,进而得到AD平分∠BAC.
证明:过D作DM⊥AB于M,DN⊥AC于N.
∵△DBE和△DCF的面积相等,
∴BE?DM=CF?DN.
又∵BE=CF,
∴DM=DN.
又∵DM⊥AB,DN⊥AC,
∴AD平分∠BAC(在角的内部,到角两边距离相等的点在角的平分线上).
点评:基本辅助线没变.
例5.如图,OP为∠AOB内一条射线,C,D分别为OA,OB上两点,且∠PCO+∠PDO=180°,PC=PD.求证:OP平分∠AOB.
分析:标图
已知可推?邻补角好找180?,可以转换为等角的条件
求证何来?“双垂等距推角分”
作双垂,欠等距,全等推
整理一下思路:
1.作双垂
2.由180?找等角,供全等用
3.证明两三角形全等
4.得距离等,配双垂证角等
证明:过点P作PM⊥OA,PN⊥OB.
则∠PMC=∠PND=90°
∵∠PCO+∠PDO=180°,
∠PCO+∠PCM=180°,
∴∠PCM=∠PDN.
在△PMC与△PND中
∴△PMC≌△PND.
∴PM=PN.
∵PM⊥OA,PN⊥OB,
∴OP平分∠AOB.
小结今天的学习内容
新的定理:在角的内部,到角的两边的距离相等的点在角的平分线上.
新的应用:“双垂距离推角分”
.
务必关注到目前学过的两个定理的异同.(基本图不变,辅助线不变)
课后作业
1.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ).
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
分析:过两把直尺的交点C作CE⊥AO,CF⊥BO,根据题意可得CE=CF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB;
解:(1)如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO.
又∵两把完全相同的长方形直尺,
∴PE=PF.
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上).
故选:A.
2.如图所示,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E,F,且BE=CF,求证:AD是△ABC的角平分线.
分析:首先可证明Rt△BDE≌Rt△DCF(HL),再根据定理2,求得AD是△ABC的角平分线即可.
证明:∵DE⊥AB,DF⊥AC,
∴在Rt△BDE与Rt△DCF中.
∴Rt△BDE≌Rt△DCF(HL).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
备用题
练习
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
分析:根据全等三角形的判定定理得出Rt△BDE≌Rt△CDF,进而得出DE=DF,由定理2可知AD是∠BAC的平分线.
证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
在Rt△BDE与Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴AD是∠BAC的平分线.
