6.4.1正弦、余弦定理(知识储备+例题分析+课堂小练)-【新教材】人教A版(2019)高中数学必修第二册同步课堂讲义(Word版含解析)
文档属性
| 名称 | 6.4.1正弦、余弦定理(知识储备+例题分析+课堂小练)-【新教材】人教A版(2019)高中数学必修第二册同步课堂讲义(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 120.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 18:26:32 | ||
图片预览

文档简介
11696700122428002020-2021学年高一数学第二学期人教版(2019)必修第二册同步课堂
第六章 平面向量及其应用
3810532765知识储备
知识储备
6.4.1正弦、余弦定理
1.余弦定理:三角形中任何一方的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即;
falsefalse,false
2.余弦定理的推论:osA=false,cosB=false,cosC=false
3.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即;
false
4.正弦定理的推论:1.false
2.false
-1524029845例题分析
例题分析
例1.在 △ABC 中,若 asinB+bsinA=2c ,则 △ABC 是________三角形.
【解析】由正弦定理可知: asinA=bsinB ,因为 asinB+bsinA=2c ,所以 sinAsinB+sinBsinA=2sinC ,
由 2sinC=sinAsinB+sinBsinA≥2sinAsinB?sinBsinA=2 ,当且仅当 sinA=sinB 时取等号,
即 a=b?A=B ,有 2sinC≥2 ,所以 sinC≥1 ,而 sinC≤1 ,所以 sinC=1 , C=π2 ,因此 △ABC 为等腰直角三角形.
故答案为:等腰直角。
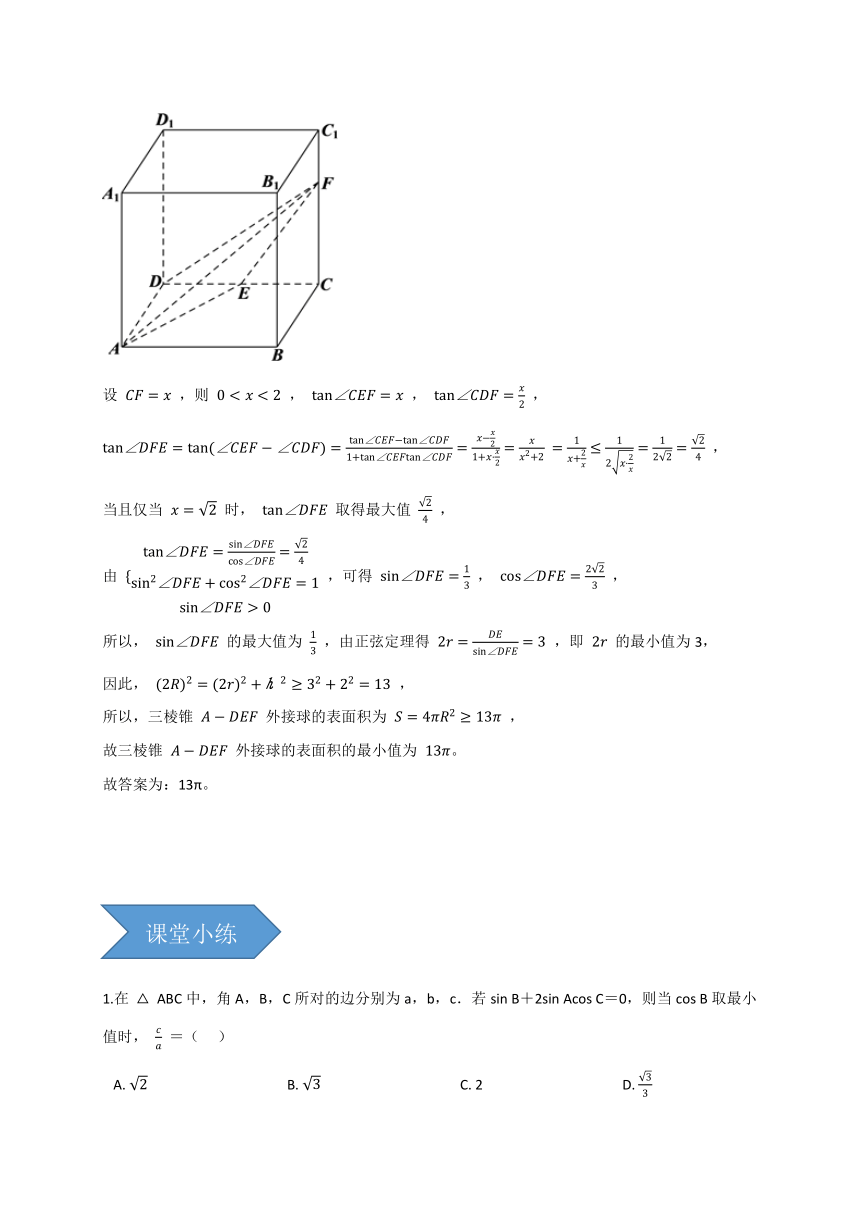
例2.在棱长为 2 的正方体 ABCD?A1B1C1D1 中, E 是 CD 的中点, F 是 CC1 上的动点,则三棱锥 A?DEF 外接球表面积的最小值为________.
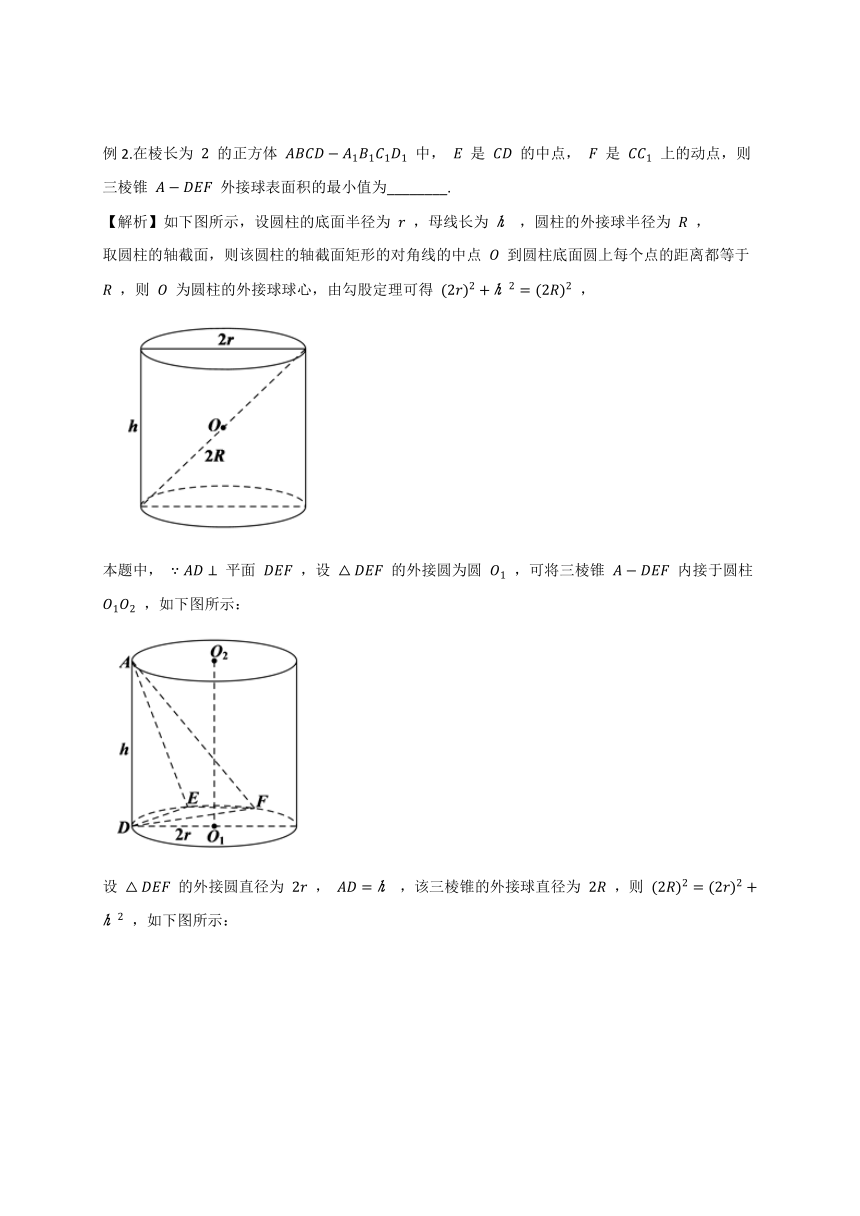
【解析】如下图所示,设圆柱的底面半径为 r ,母线长为 ? ,圆柱的外接球半径为 R ,
取圆柱的轴截面,则该圆柱的轴截面矩形的对角线的中点 O 到圆柱底面圆上每个点的距离都等于 R ,则 O 为圆柱的外接球球心,由勾股定理可得 (2r)2+?2=(2R)2 ,
?
本题中, ∵AD⊥ 平面 DEF ,设 △DEF 的外接圆为圆 O1 ,可将三棱锥 A?DEF 内接于圆柱 O1O2 ,如下图所示:
设 △DEF 的外接圆直径为 2r , AD=? ,该三棱锥的外接球直径为 2R ,则 (2R)2=(2r)2+?2 ,如下图所示:
设 CF=x ,则 0tan∠DFE=tan(∠CEF?∠CDF)=tan∠CEF?tan∠CDF1+tan∠CEFtan∠CDF=x?x21+x?x2=xx2+2 =1x+2x≤12x?2x=122=24 ,
当且仅当 x=2 时, tan∠DFE 取得最大值 24 ,
由 {tan∠DFE=sin∠DFEcos∠DFE=24sin2∠DFE+cos2∠DFE=1sin∠DFE>0 ,可得 sin∠DFE=13 , cos∠DFE=223 ,
所以, sin∠DFE 的最大值为 13 ,由正弦定理得 2r=DEsin∠DFE=3 ,即 2r 的最小值为3,
因此, (2R)2=(2r)2+?2≥32+22=13 ,
所以,三棱锥 A?DEF 外接球的表面积为 S=4πR2≥13π ,
故三棱锥 A?DEF 外接球的表面积的最小值为 13π。
故答案为:13π。
-5715125095课堂小练
课堂小练
1.在 △ ABC中,角A,B,C所对的边分别为a,b,c.若sin B+2sin Acos C=0,则当cos B取最小值时, ca =(??? )
A.?2????????????????????????????????????????B.?3????????????????????????????????????????C.?2????????????????????????????????????????D.?33
2.已知点 P(3,4) 是椭圆 x2a2+y2b2=1(a>b>0) 上一点, F1 、 F2 是椭圆的两个焦点,若 PF1?PF2=0 ,求椭圆的方程(??? )
A.?x236+y220=1???????????????????B.?x216+y236=1???????????????????C.?x225+y210=1???????????????????D.?x245+y220=1
3.为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在 B 点处的测量觇标高10米,攀登者们在 A 处测得到觇标底点 B 和顶点 C 的仰角分别为 70° , 80° ,则 A 、 B 的高度差约为(??? )
(参考数据: sin10°≈0.1736 , sin70°≈0.9397 , sin80°≈0.9848 )
A.?10米?????????????????????????????????B.?9.66米?????????????????????????????????C.?9.40米?????????????????????????????????D.?8.66米
4.在 △ABC 中,角 A,B,C 所对的边分别是 a,b,c ,则“ asinB=b+csinC+sinA ”是“ △ABC 为等腰三角形”的(??? )
A.?充分不必要条件?????????????B.?必要不充分条件?????????????C.?充要条件?????????????D.?既不充分也不必要条件
5.在三棱锥 P?ABC 中, PB=PC=AB=AC=BC=4 , PA=23 ,则异面直线PC与AB所成角的余弦值是(??? )
A.?18??????????????????????????????????????????B.?16??????????????????????????????????????????C.?14??????????????????????????????????????????D.?13
80010355600答案解析
答案解析
1.【答案】 B
【解析】由sin B+2sin Acos C=0,根据正弦定理和余弦定理得 b+2a?a2+b2?c22ab=0 ,
∴ a2+2b2?c2=0 ,∴ b2=c2?a22 ,
∴ cosB=a2+c2?b22ac=3a2+c24ac=3a4c+c4a≥32 ,
当且仅当 3a4c=c4a ,即 ca=3 时取等号,cos B取最小值 32 .
故答案为:B.
2.【答案】 D
【解析】因为 F1 、 F2 是椭圆的两个焦点,
所以不妨设 F1 为左焦点坐标为 (?c,0) 、 F2 为右焦点坐标为 (c,0) .
因为 PF1?PF2=0 ,
所以有 (3+c,4)?(3?c,4)=0?(3+c)(3?c)+16=0?c2=25 ,
因此 a2?b2=25(1) ,
又因为点 P(3,4) 是椭圆 x2a2+y2b2=1(a>b>0) 上一点,
所以 9a2+16b2=1(2) ,由 (1)(2) 解得: {a2=45b2=20 ,所以椭圆的方程为: x245+y220=1 ,
故答案为:D
3.【答案】 C
【解析】如图所示,
在 △ABC 中,由正弦定理可得 BCsin∠BAC=ABsin∠ACB ,
由 ∠BAC=∠DAC?∠BAD=10? , ∠ACD=90??∠CAD=10? ,
所以 AB=BC=10 ,
在 Rt△ADB 中, BD=ABsin∠BAD=10sin70?≈9.40 .
故答案为:C.
4.【答案】 A
【解析】充分性: ∵asinB=b+csinC+sinA ,得 ab=b+cc+a ,可得 a2+ac=b2+bc ,
则 a2?b2+ac?bc=0 ,即 (a?b)(a+b+c)=0 , ∵a+b+c>0 , ∴a=b ,
所以, △ABC 为等腰三角形,即充分性成立;
必要性:若 △ABC 为等腰三角形,则 a=c 或 b=c ,那么等式 asinB=b+csinC+sinA 不一定成立,即必要性不成立,
故答案为:A
5.【答案】 A
【解析】分别取 PA 、 PB 、 PC 的中点 E 、 F 、 G ,连接 EF 、 EG 、 FG 、 GA 、 PG ,如图:
由 PB=PC=AB=AC=BC=4 可得 PG=AG=32BC=23 ,所以 EG⊥PA ,
在 △GPA , PG=AG=PA=23 ,可得 EG=3
由中位线的性质可得 EF//AB 且 EF=12AB=2 , FG//PC 且 FG=12PC=2 ,
所以 ∠GFE 或其补角即为异面直线PC与AB所成角,
在 △GFE 中, cos∠GFE=GF2+EF2?GE22GF?EF=4+4?92×2×2=?18 ,
所以异面直线AB与PC所成角的余弦值为 18 ,
故答案为:A.
第六章 平面向量及其应用
3810532765知识储备
知识储备
6.4.1正弦、余弦定理
1.余弦定理:三角形中任何一方的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即;
falsefalse,false
2.余弦定理的推论:osA=false,cosB=false,cosC=false
3.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即;
false
4.正弦定理的推论:1.false
2.false
-1524029845例题分析
例题分析
例1.在 △ABC 中,若 asinB+bsinA=2c ,则 △ABC 是________三角形.
【解析】由正弦定理可知: asinA=bsinB ,因为 asinB+bsinA=2c ,所以 sinAsinB+sinBsinA=2sinC ,
由 2sinC=sinAsinB+sinBsinA≥2sinAsinB?sinBsinA=2 ,当且仅当 sinA=sinB 时取等号,
即 a=b?A=B ,有 2sinC≥2 ,所以 sinC≥1 ,而 sinC≤1 ,所以 sinC=1 , C=π2 ,因此 △ABC 为等腰直角三角形.
故答案为:等腰直角。
例2.在棱长为 2 的正方体 ABCD?A1B1C1D1 中, E 是 CD 的中点, F 是 CC1 上的动点,则三棱锥 A?DEF 外接球表面积的最小值为________.
【解析】如下图所示,设圆柱的底面半径为 r ,母线长为 ? ,圆柱的外接球半径为 R ,
取圆柱的轴截面,则该圆柱的轴截面矩形的对角线的中点 O 到圆柱底面圆上每个点的距离都等于 R ,则 O 为圆柱的外接球球心,由勾股定理可得 (2r)2+?2=(2R)2 ,
?
本题中, ∵AD⊥ 平面 DEF ,设 △DEF 的外接圆为圆 O1 ,可将三棱锥 A?DEF 内接于圆柱 O1O2 ,如下图所示:
设 △DEF 的外接圆直径为 2r , AD=? ,该三棱锥的外接球直径为 2R ,则 (2R)2=(2r)2+?2 ,如下图所示:
设 CF=x ,则 0
当且仅当 x=2 时, tan∠DFE 取得最大值 24 ,
由 {tan∠DFE=sin∠DFEcos∠DFE=24sin2∠DFE+cos2∠DFE=1sin∠DFE>0 ,可得 sin∠DFE=13 , cos∠DFE=223 ,
所以, sin∠DFE 的最大值为 13 ,由正弦定理得 2r=DEsin∠DFE=3 ,即 2r 的最小值为3,
因此, (2R)2=(2r)2+?2≥32+22=13 ,
所以,三棱锥 A?DEF 外接球的表面积为 S=4πR2≥13π ,
故三棱锥 A?DEF 外接球的表面积的最小值为 13π。
故答案为:13π。
-5715125095课堂小练
课堂小练
1.在 △ ABC中,角A,B,C所对的边分别为a,b,c.若sin B+2sin Acos C=0,则当cos B取最小值时, ca =(??? )
A.?2????????????????????????????????????????B.?3????????????????????????????????????????C.?2????????????????????????????????????????D.?33
2.已知点 P(3,4) 是椭圆 x2a2+y2b2=1(a>b>0) 上一点, F1 、 F2 是椭圆的两个焦点,若 PF1?PF2=0 ,求椭圆的方程(??? )
A.?x236+y220=1???????????????????B.?x216+y236=1???????????????????C.?x225+y210=1???????????????????D.?x245+y220=1
3.为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在 B 点处的测量觇标高10米,攀登者们在 A 处测得到觇标底点 B 和顶点 C 的仰角分别为 70° , 80° ,则 A 、 B 的高度差约为(??? )
(参考数据: sin10°≈0.1736 , sin70°≈0.9397 , sin80°≈0.9848 )
A.?10米?????????????????????????????????B.?9.66米?????????????????????????????????C.?9.40米?????????????????????????????????D.?8.66米
4.在 △ABC 中,角 A,B,C 所对的边分别是 a,b,c ,则“ asinB=b+csinC+sinA ”是“ △ABC 为等腰三角形”的(??? )
A.?充分不必要条件?????????????B.?必要不充分条件?????????????C.?充要条件?????????????D.?既不充分也不必要条件
5.在三棱锥 P?ABC 中, PB=PC=AB=AC=BC=4 , PA=23 ,则异面直线PC与AB所成角的余弦值是(??? )
A.?18??????????????????????????????????????????B.?16??????????????????????????????????????????C.?14??????????????????????????????????????????D.?13
80010355600答案解析
答案解析
1.【答案】 B
【解析】由sin B+2sin Acos C=0,根据正弦定理和余弦定理得 b+2a?a2+b2?c22ab=0 ,
∴ a2+2b2?c2=0 ,∴ b2=c2?a22 ,
∴ cosB=a2+c2?b22ac=3a2+c24ac=3a4c+c4a≥32 ,
当且仅当 3a4c=c4a ,即 ca=3 时取等号,cos B取最小值 32 .
故答案为:B.
2.【答案】 D
【解析】因为 F1 、 F2 是椭圆的两个焦点,
所以不妨设 F1 为左焦点坐标为 (?c,0) 、 F2 为右焦点坐标为 (c,0) .
因为 PF1?PF2=0 ,
所以有 (3+c,4)?(3?c,4)=0?(3+c)(3?c)+16=0?c2=25 ,
因此 a2?b2=25(1) ,
又因为点 P(3,4) 是椭圆 x2a2+y2b2=1(a>b>0) 上一点,
所以 9a2+16b2=1(2) ,由 (1)(2) 解得: {a2=45b2=20 ,所以椭圆的方程为: x245+y220=1 ,
故答案为:D
3.【答案】 C
【解析】如图所示,
在 △ABC 中,由正弦定理可得 BCsin∠BAC=ABsin∠ACB ,
由 ∠BAC=∠DAC?∠BAD=10? , ∠ACD=90??∠CAD=10? ,
所以 AB=BC=10 ,
在 Rt△ADB 中, BD=ABsin∠BAD=10sin70?≈9.40 .
故答案为:C.
4.【答案】 A
【解析】充分性: ∵asinB=b+csinC+sinA ,得 ab=b+cc+a ,可得 a2+ac=b2+bc ,
则 a2?b2+ac?bc=0 ,即 (a?b)(a+b+c)=0 , ∵a+b+c>0 , ∴a=b ,
所以, △ABC 为等腰三角形,即充分性成立;
必要性:若 △ABC 为等腰三角形,则 a=c 或 b=c ,那么等式 asinB=b+csinC+sinA 不一定成立,即必要性不成立,
故答案为:A
5.【答案】 A
【解析】分别取 PA 、 PB 、 PC 的中点 E 、 F 、 G ,连接 EF 、 EG 、 FG 、 GA 、 PG ,如图:
由 PB=PC=AB=AC=BC=4 可得 PG=AG=32BC=23 ,所以 EG⊥PA ,
在 △GPA , PG=AG=PA=23 ,可得 EG=3
由中位线的性质可得 EF//AB 且 EF=12AB=2 , FG//PC 且 FG=12PC=2 ,
所以 ∠GFE 或其补角即为异面直线PC与AB所成角,
在 △GFE 中, cos∠GFE=GF2+EF2?GE22GF?EF=4+4?92×2×2=?18 ,
所以异面直线AB与PC所成角的余弦值为 18 ,
故答案为:A.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
