6.3.2平面向量的数量积(知识储备+例题分析+课堂小练)-【新教材】人教A版(2019)高中数学必修第二册同步课堂讲义(Word版含解析)
文档属性
| 名称 | 6.3.2平面向量的数量积(知识储备+例题分析+课堂小练)-【新教材】人教A版(2019)高中数学必修第二册同步课堂讲义(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览

文档简介
2020-2021学年高一数学第二学期人教版(2019)必修第二册同步课堂
第六章 平面向量及其应用
3810532765知识储备
知识储备
6.3.2平面向量的数量积
1.平面向量的数量积:已知两个非零向量a与b,我们把数量|a||b|cosfalse叫作a与b的数量积(或内积),记 作a·b,即a·b=|a| |b|cosfalse.其中false是a与b的 夹角,la|cosfalse( |b |cosfalse)叫作向量a在b方向上(b在a方向上)的投影.
规定:零向量与任一向量的数量积为0.
2.平面向量数量积的几何意义:数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosfalse的乘积.
3.平面向量数量积的性质:设a和b都是非零向量,则
(1)如果e是单位向量,则a·e=e·a=la|cosfalse.
(2)a⊥bfalsea·b=0.
(3)当a与b同向时,a·b=|a| |b|
当a与b反向时a·b=-la| |b|
特别地:a·a=|a|false或|a|=false
(4)cosfalse=false
-1524029845例题分析
例题分析
例1.已知平面向量 a 、 b 满足 |a|=|a+2b|=3 ,则 3|b|+|a+b| 的最大值为________.
【解析】 ∵|a+2b|2=a2+4a?b+4b2=3+4a?b+4b2=3 ,则 a?b=?b2 ,
设 a 与 b 的夹角为 θ ,则 |a|?|b|cosθ=?|b|2 , ∴|b|=?3cosθ ,
∵|b|≥0 , 0≤θ≤π ,可得 π2≤θ≤π ,
|a+b|2=a2+2a?b+b2=3?|b|2=3sin2θ ,则 |a+b|=3sinθ ,
所以, 3|b|+|a+b|=?3cosθ+3sinθ=23sin(θ?π3) ,
∵π2≤θ≤π ,则 π6≤θ?π3≤2π3 ,所以,当 θ?π3=π2 时, 3|b|+|a+b| 取最大值 23 .
故答案为: 23 .
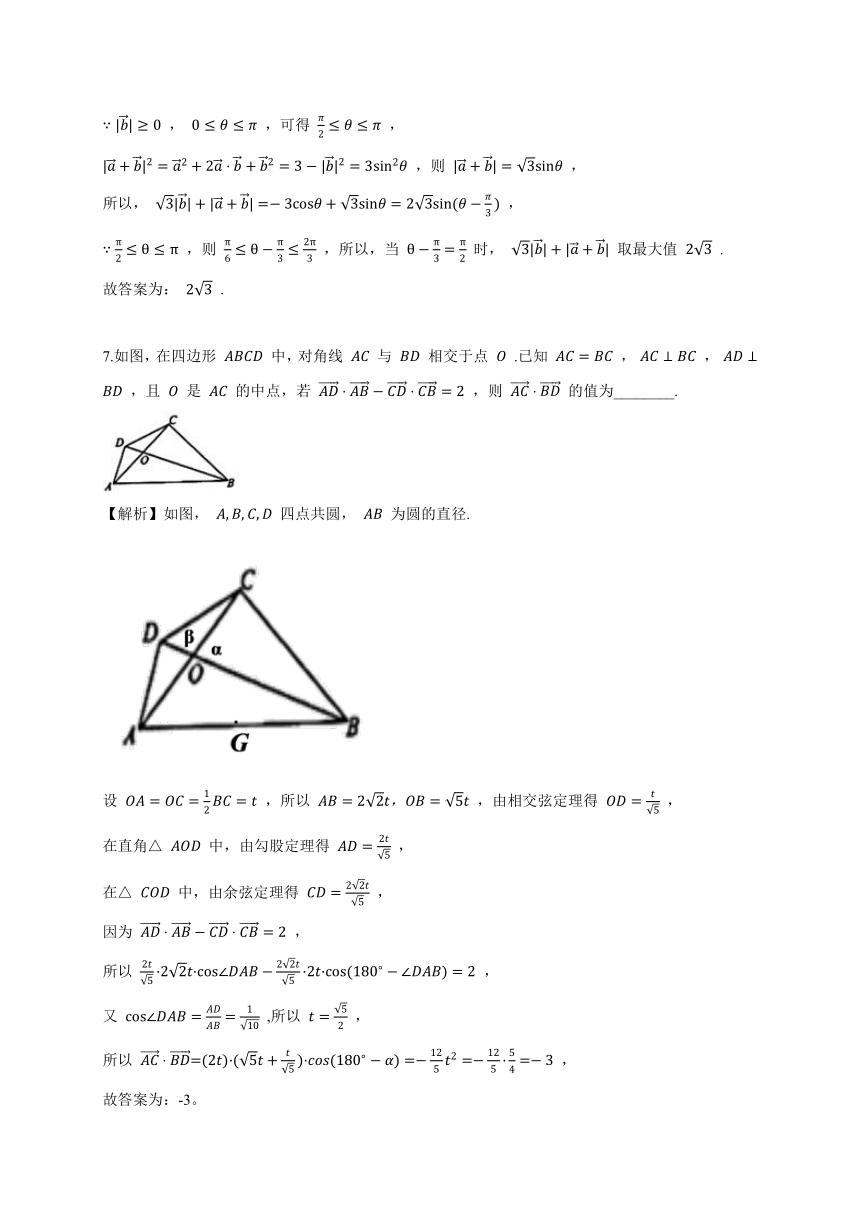
7.如图,在四边形 ABCD 中,对角线 AC 与 BD 相交于点 O .已知 AC=BC , AC⊥BC , AD⊥BD ,且 O 是 AC 的中点,若 AD?AB?CD?CB=2 ,则 AC?BD 的值为________.
【解析】如图, A,B,C,D 四点共圆, AB 为圆的直径.
设 OA=OC=12BC=t ,所以 AB=22t,OB=5t ,由相交弦定理得 OD=t5 ,
在直角△ AOD 中,由勾股定理得 AD=2t5 ,
在△ COD 中,由余弦定理得 CD=22t5 ,
因为 AD?AB?CD?CB=2 ,
所以 2t5·22t·cos∠DAB?22t5·2t·cos(180??∠DAB)=2 ,
又 cos∠DAB=ADAB=110 ,所以 t=52 ,
所以 AC?BD=(2t)·(5t+t5)·cos(180??α)=?125t2=?125·54=?3 ,
故答案为:-3。
-5715125095课堂小练
课堂小练
1.在 △ABC 中, AB=3 , AC=2 , ∠BAC=60° ,点 D , E 分别在线段 AB , CD 上,且 BD=2AD , CE=2ED ,则 BE?AB= (??? ).
A.?-3??????????????????????????????????????????B.?-6??????????????????????????????????????????C.?4??????????????????????????????????????????D.?9
2.如图, AB 是单位圆 O 的直径,点 C , D 是半圆弧 AB 上的两个三等分点,则 AC?AD= (??? )
A.?1?????????????????????????????????????????B.?32?????????????????????????????????????????C.?32?????????????????????????????????????????D.?3
3.已知 e1,e2 为单位向量,且 |e1+2e2|≤2 ,若非零向量 a 满足 a?e1≤a?e2 ,则 a?(2e1+e2)|a| 的最大值是(??? )
A.?334???????????????????????????????????B.?332???????????????????????????????????C.?362???????????????????????????????????D.?364
4.直线 ax+by+c=0 与圆 C : x2?2x+y2+4y=0 相交于 A , B 两点,且 |AB|=15 ,则 CA?CB= (??? )
A.??52????????????????????????????????????B.?532????????????????????????????????????C.?32????????????????????????????????????D.??32
5.已知 △OAB , OA=1 , OB=2 , OA?OB=?1 ,过点 O 作 OD 垂直 AB 于点 D ,点 E 满足 OE=12ED ,则 EO?EA 的值为(??? )
A.??328??????????????????????????????????B.??121??????????????????????????????????C.??29??????????????????????????????????D.??221
80010355600答案解析
答案解析
1.【答案】 B
【解析】根据题意, AB=3,BD=2AD ,则 AD=1
在 △ADC 中,又 AC=2 , ∠BAC=60°
则 DC2=AD2+AC2?2AD?DCcos∠BAC=3
则 DC=3
则 CD⊥AB
则 BE?AB=(BD+DE)?AB=BD?AB+DE?AB=BD?AB=3×2×cos180?=?6
故答案为:B
2.【答案】 C
【解析】连接 OD,OC ,则 ∠AOD=2π3,∠CAD=π6,AC=1 ,
在 △AOD 中,由余弦定理得: AD2=12+12?2×1×1×(?12)=3,∴AD=3 ,
所以 AC?AD=1×3×cosπ6=32 ,
故答案为:C。
3.【答案】 D
【解析】由题意,可设 e1=(1,0) , e2=(cosα,sinα) ,则 e1+2e2=(1+2cosα,2sinα) ,
由 |e1+2e2|≤2 ,可得 (1+2cosα)2+4sin2α≤4 ,整理得 cosα≤?14 ,
设 a=(rcosβ,rsinβ) , r>0 ,
由 a?e1≤a?e2 ,可得 (rcosβ,rsinβ)?(1,0)≤(rcosβ,rsinβ)?(cosα,sinα) ,
即 rcosβ≤rcosβcosα+rsinβsinα ,所以 cosβ≤cos(α?β) ,
当 cosβ=cos(α?β) 时, β=α?β+2kπ(k∈Z) 或 β=?α+β+2kπ(k∈Z) ,
即 2β=α+2kπ(k∈Z) 或 α=2kπ(k∈Z) ,
因为 cosα≤?14 ,所以 α=2kπ(k∈Z) 不符合题意,
故 cosβ=cos(α?β) 时, 2β=α+2kπ(k∈Z) .
而 a?(2e1+e2)|a|=2rcosβ+rcosβcosα+rsinβsinαr=2cosβ+cos(α?β) ,
因为 cosβ≤cos(α?β) ,所以 a?(2e1+e2)|a| ≤3cos(α?β) ,
当 2β=α+2kπ(k∈Z) 时,等号成立,此时 3cos(α?β)=3cos(β?2kπ)=3cosβ ,
因为 cosα=cos(2β?2kπ)=cos2β=2cos2β?1≤?14 ,所以 cos2β≤38 ,即 ?64≤cosβ≤64 ,
所以 a?(2e1+e2)|a| ≤3cos(α?β)=3cosβ≤364 .
故答案为:D.
4.【答案】 A
【解析】圆 C 标准方程为 (x?1)2+(y+2)2=5 ,圆心半径为 r=5 ,
在△ABC 中,利用余弦定理,得: cos∠ACB=CA2+CB2?AB22CA?CB=5+5?152×5×5=?12 ,
∴ CA?CB=|CA||CB|cos∠ACB=5×5×(?12)=?52 ,
故答案为:A.
5.【答案】 D
【解析】由题意,作出图形,如图,
∵OA=1 , OB=2 , OA?OB=?1
∴OA?OB=1×2cos∠AOB=2cos∠AOB=?1 , ∴cos∠AOB=?12 ,
由 ∠AOB∈(0,π) 可得 ∠AOB=2π3 ,
∴AB=OA2+OB2?2?OA?OB?cos∠AOB=7 ,
又 S△AOB=12?OA?OB?sin∠AOB=12?OD?AB=32 ,则 OD=37 ,
∴EO?EA=?OE?(ED+DA)=?2OE2=?29?OD2=?29×37=?221 .
故答案为:D.
第六章 平面向量及其应用
3810532765知识储备
知识储备
6.3.2平面向量的数量积
1.平面向量的数量积:已知两个非零向量a与b,我们把数量|a||b|cosfalse叫作a与b的数量积(或内积),记 作a·b,即a·b=|a| |b|cosfalse.其中false是a与b的 夹角,la|cosfalse( |b |cosfalse)叫作向量a在b方向上(b在a方向上)的投影.
规定:零向量与任一向量的数量积为0.
2.平面向量数量积的几何意义:数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosfalse的乘积.
3.平面向量数量积的性质:设a和b都是非零向量,则
(1)如果e是单位向量,则a·e=e·a=la|cosfalse.
(2)a⊥bfalsea·b=0.
(3)当a与b同向时,a·b=|a| |b|
当a与b反向时a·b=-la| |b|
特别地:a·a=|a|false或|a|=false
(4)cosfalse=false
-1524029845例题分析
例题分析
例1.已知平面向量 a 、 b 满足 |a|=|a+2b|=3 ,则 3|b|+|a+b| 的最大值为________.
【解析】 ∵|a+2b|2=a2+4a?b+4b2=3+4a?b+4b2=3 ,则 a?b=?b2 ,
设 a 与 b 的夹角为 θ ,则 |a|?|b|cosθ=?|b|2 , ∴|b|=?3cosθ ,
∵|b|≥0 , 0≤θ≤π ,可得 π2≤θ≤π ,
|a+b|2=a2+2a?b+b2=3?|b|2=3sin2θ ,则 |a+b|=3sinθ ,
所以, 3|b|+|a+b|=?3cosθ+3sinθ=23sin(θ?π3) ,
∵π2≤θ≤π ,则 π6≤θ?π3≤2π3 ,所以,当 θ?π3=π2 时, 3|b|+|a+b| 取最大值 23 .
故答案为: 23 .
7.如图,在四边形 ABCD 中,对角线 AC 与 BD 相交于点 O .已知 AC=BC , AC⊥BC , AD⊥BD ,且 O 是 AC 的中点,若 AD?AB?CD?CB=2 ,则 AC?BD 的值为________.
【解析】如图, A,B,C,D 四点共圆, AB 为圆的直径.
设 OA=OC=12BC=t ,所以 AB=22t,OB=5t ,由相交弦定理得 OD=t5 ,
在直角△ AOD 中,由勾股定理得 AD=2t5 ,
在△ COD 中,由余弦定理得 CD=22t5 ,
因为 AD?AB?CD?CB=2 ,
所以 2t5·22t·cos∠DAB?22t5·2t·cos(180??∠DAB)=2 ,
又 cos∠DAB=ADAB=110 ,所以 t=52 ,
所以 AC?BD=(2t)·(5t+t5)·cos(180??α)=?125t2=?125·54=?3 ,
故答案为:-3。
-5715125095课堂小练
课堂小练
1.在 △ABC 中, AB=3 , AC=2 , ∠BAC=60° ,点 D , E 分别在线段 AB , CD 上,且 BD=2AD , CE=2ED ,则 BE?AB= (??? ).
A.?-3??????????????????????????????????????????B.?-6??????????????????????????????????????????C.?4??????????????????????????????????????????D.?9
2.如图, AB 是单位圆 O 的直径,点 C , D 是半圆弧 AB 上的两个三等分点,则 AC?AD= (??? )
A.?1?????????????????????????????????????????B.?32?????????????????????????????????????????C.?32?????????????????????????????????????????D.?3
3.已知 e1,e2 为单位向量,且 |e1+2e2|≤2 ,若非零向量 a 满足 a?e1≤a?e2 ,则 a?(2e1+e2)|a| 的最大值是(??? )
A.?334???????????????????????????????????B.?332???????????????????????????????????C.?362???????????????????????????????????D.?364
4.直线 ax+by+c=0 与圆 C : x2?2x+y2+4y=0 相交于 A , B 两点,且 |AB|=15 ,则 CA?CB= (??? )
A.??52????????????????????????????????????B.?532????????????????????????????????????C.?32????????????????????????????????????D.??32
5.已知 △OAB , OA=1 , OB=2 , OA?OB=?1 ,过点 O 作 OD 垂直 AB 于点 D ,点 E 满足 OE=12ED ,则 EO?EA 的值为(??? )
A.??328??????????????????????????????????B.??121??????????????????????????????????C.??29??????????????????????????????????D.??221
80010355600答案解析
答案解析
1.【答案】 B
【解析】根据题意, AB=3,BD=2AD ,则 AD=1
在 △ADC 中,又 AC=2 , ∠BAC=60°
则 DC2=AD2+AC2?2AD?DCcos∠BAC=3
则 DC=3
则 CD⊥AB
则 BE?AB=(BD+DE)?AB=BD?AB+DE?AB=BD?AB=3×2×cos180?=?6
故答案为:B
2.【答案】 C
【解析】连接 OD,OC ,则 ∠AOD=2π3,∠CAD=π6,AC=1 ,
在 △AOD 中,由余弦定理得: AD2=12+12?2×1×1×(?12)=3,∴AD=3 ,
所以 AC?AD=1×3×cosπ6=32 ,
故答案为:C。
3.【答案】 D
【解析】由题意,可设 e1=(1,0) , e2=(cosα,sinα) ,则 e1+2e2=(1+2cosα,2sinα) ,
由 |e1+2e2|≤2 ,可得 (1+2cosα)2+4sin2α≤4 ,整理得 cosα≤?14 ,
设 a=(rcosβ,rsinβ) , r>0 ,
由 a?e1≤a?e2 ,可得 (rcosβ,rsinβ)?(1,0)≤(rcosβ,rsinβ)?(cosα,sinα) ,
即 rcosβ≤rcosβcosα+rsinβsinα ,所以 cosβ≤cos(α?β) ,
当 cosβ=cos(α?β) 时, β=α?β+2kπ(k∈Z) 或 β=?α+β+2kπ(k∈Z) ,
即 2β=α+2kπ(k∈Z) 或 α=2kπ(k∈Z) ,
因为 cosα≤?14 ,所以 α=2kπ(k∈Z) 不符合题意,
故 cosβ=cos(α?β) 时, 2β=α+2kπ(k∈Z) .
而 a?(2e1+e2)|a|=2rcosβ+rcosβcosα+rsinβsinαr=2cosβ+cos(α?β) ,
因为 cosβ≤cos(α?β) ,所以 a?(2e1+e2)|a| ≤3cos(α?β) ,
当 2β=α+2kπ(k∈Z) 时,等号成立,此时 3cos(α?β)=3cos(β?2kπ)=3cosβ ,
因为 cosα=cos(2β?2kπ)=cos2β=2cos2β?1≤?14 ,所以 cos2β≤38 ,即 ?64≤cosβ≤64 ,
所以 a?(2e1+e2)|a| ≤3cos(α?β)=3cosβ≤364 .
故答案为:D.
4.【答案】 A
【解析】圆 C 标准方程为 (x?1)2+(y+2)2=5 ,圆心半径为 r=5 ,
在△ABC 中,利用余弦定理,得: cos∠ACB=CA2+CB2?AB22CA?CB=5+5?152×5×5=?12 ,
∴ CA?CB=|CA||CB|cos∠ACB=5×5×(?12)=?52 ,
故答案为:A.
5.【答案】 D
【解析】由题意,作出图形,如图,
∵OA=1 , OB=2 , OA?OB=?1
∴OA?OB=1×2cos∠AOB=2cos∠AOB=?1 , ∴cos∠AOB=?12 ,
由 ∠AOB∈(0,π) 可得 ∠AOB=2π3 ,
∴AB=OA2+OB2?2?OA?OB?cos∠AOB=7 ,
又 S△AOB=12?OA?OB?sin∠AOB=12?OD?AB=32 ,则 OD=37 ,
∴EO?EA=?OE?(ED+DA)=?2OE2=?29?OD2=?29×37=?221 .
故答案为:D.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
