山东省济宁市高新区2020-2021学年六年级下学期期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 山东省济宁市高新区2020-2021学年六年级下学期期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览


文档简介
2020-2021学年山东省济宁市高新区六年级(下)期末数学试卷(五四学制)
一.选择题(本大题满分30分,每小题3分)
1.以下调查方式比较合理的是( )
A.了解全国学生周末使用网络情况,采用普查的方式
B.了解全国七年级学生节约用水的情况,采用抽样调查的方式
C.了解一沓钞票中有没有假钞,采用抽样调查的方式
D.了解全国中学生心理健康现状,采用普查的方式
2.下列计算正确的是( )
A.
B.(a2)3=a5
C.a﹣1÷a﹣3=a2
D.(a+b)2=a2+b2
3.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1
B.2
C.3
D.4
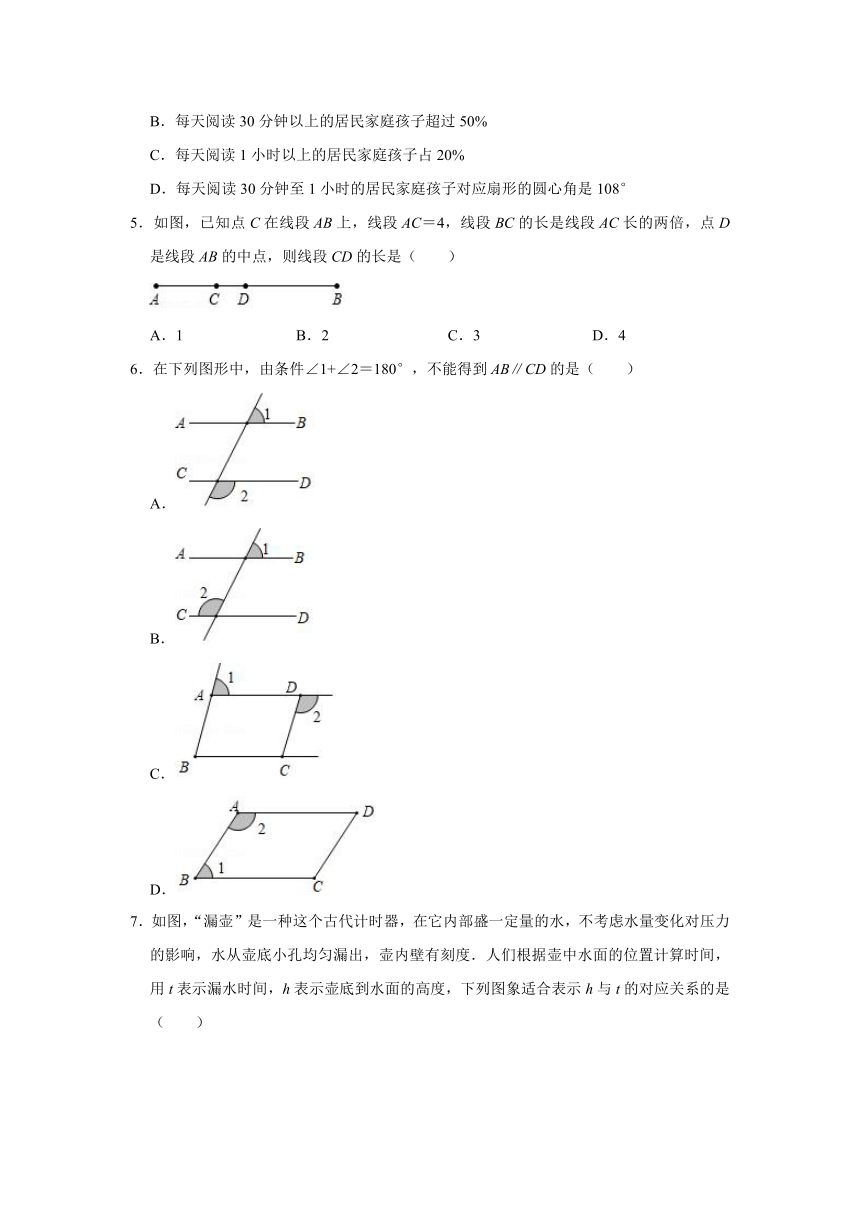
4.根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )
A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
5.如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,则线段CD的长是( )
A.1
B.2
C.3
D.4
6.在下列图形中,由条件∠1+∠2=180°,不能得到AB∥CD的是( )
A.
B.
C.
D.
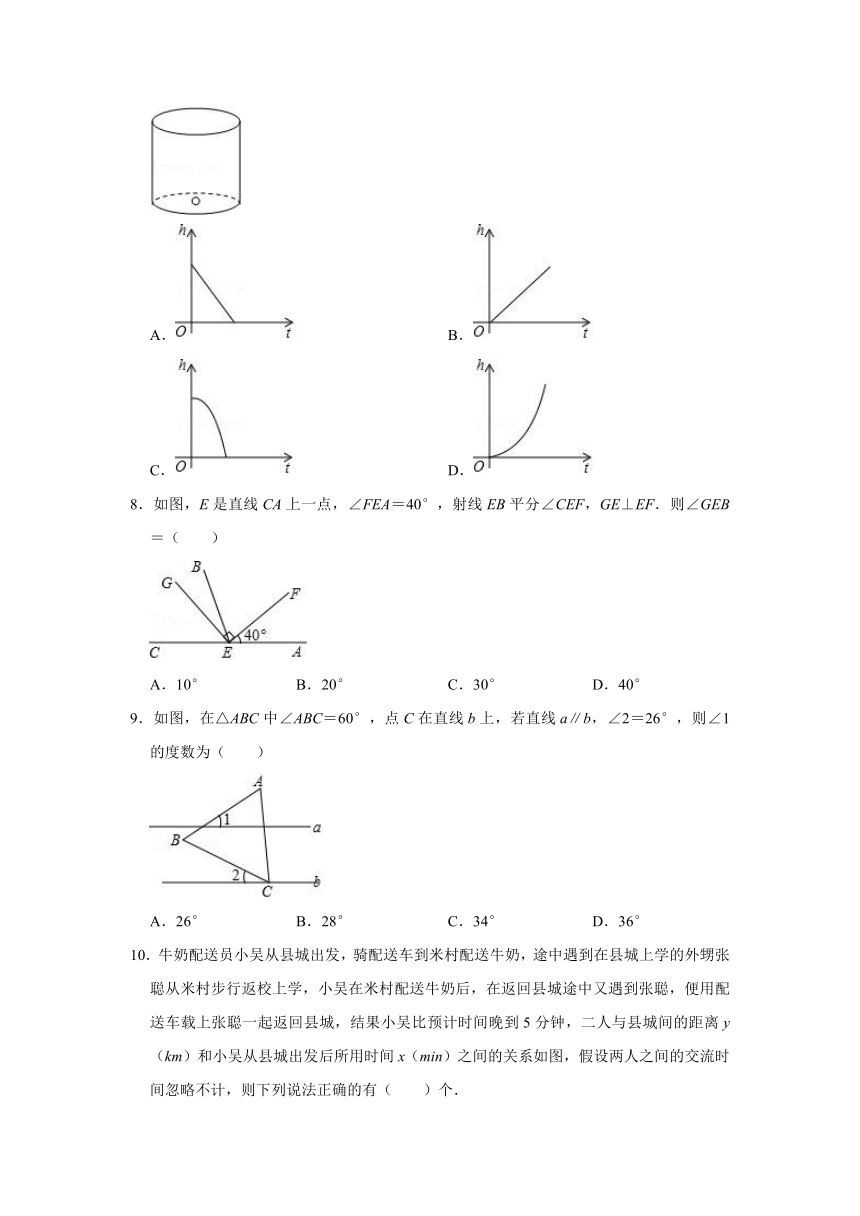
7.如图,“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,h表示壶底到水面的高度,下列图象适合表示h与t的对应关系的是( )
A.
B.
C.
D.
8.如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10°
B.20°
C.30°
D.40°
9.如图,在△ABC中∠ABC=60°,点C在直线b上,若直线a∥b,∠2=26°,则∠1的度数为( )
A.26°
B.28°
C.34°
D.36°
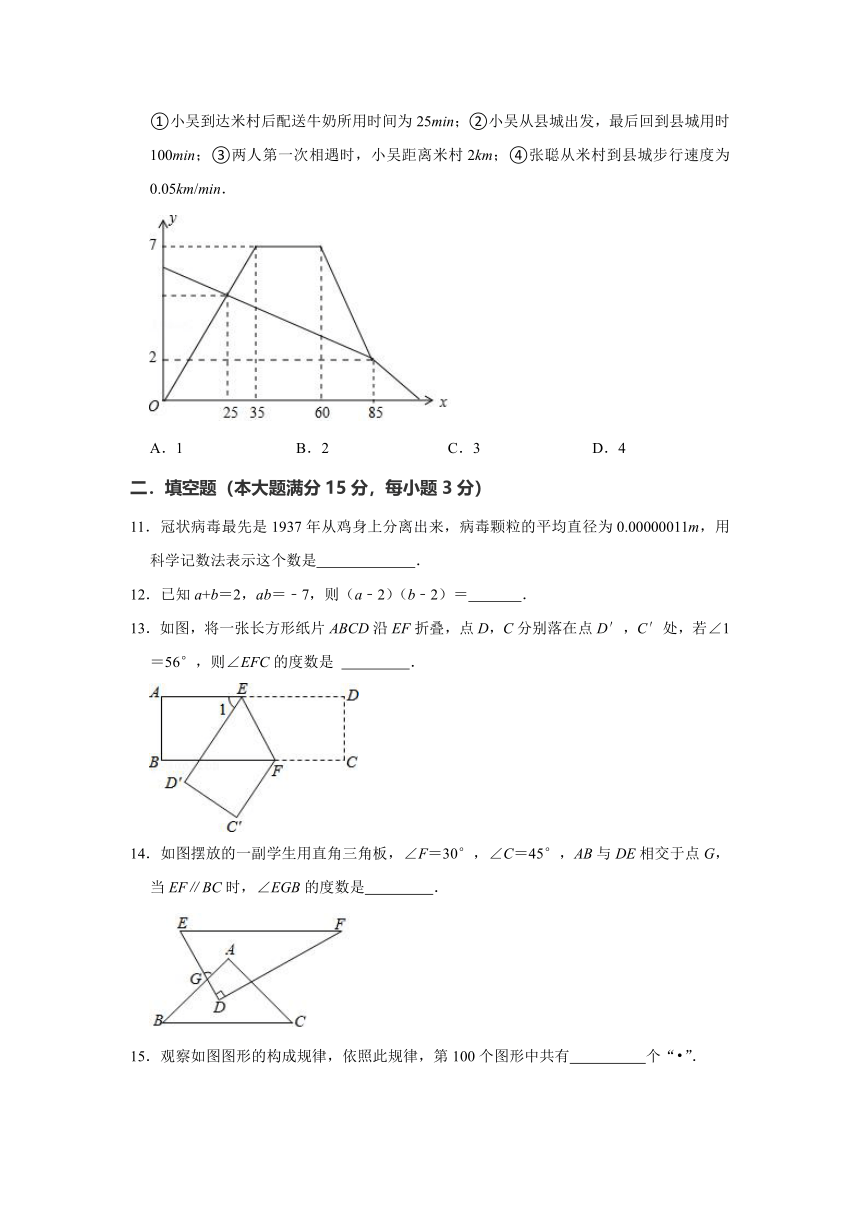
10.牛奶配送员小吴从县城出发,骑配送车到米村配送牛奶,途中遇到在县城上学的外甥张聪从米村步行返校上学,小吴在米村配送牛奶后,在返回县城途中又遇到张聪,便用配送车载上张聪一起返回县城,结果小吴比预计时间晚到5分钟,二人与县城间的距离y(km)和小吴从县城出发后所用时间x(min)之间的关系如图,假设两人之间的交流时间忽略不计,则下列说法正确的有( )个.
①小吴到达米村后配送牛奶所用时间为25min;②小吴从县城出发,最后回到县城用时100min;③两人第一次相遇时,小吴距离米村2km;④张聪从米村到县城步行速度为0.05km/min.
A.1
B.2
C.3
D.4
二.填空题(本大题满分15分,每小题3分)
11.冠状病毒最先是1937年从鸡身上分离出来,病毒颗粒的平均直径为0.00000011m,用科学记数法表示这个数是
.
12.已知a+b=2,ab=﹣7,则(a﹣2)(b﹣2)=
.
13.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D′,C′处,若∠1=56°,则∠EFC的度数是
.
14.如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是
.
15.观察如图图形的构成规律,依照此规律,第100个图形中共有
个“?”.
三.解答题(本大题满分35分,解答题写出必要的文字说明或推演步骤)
16计算:
(1)(﹣a)3?a2﹣(﹣3a3)2÷a.
(2)20212﹣2022×2020.
17先化简,再求值:a(a+6)﹣(a+3)(a﹣3)+(2a﹣1)2,其中a=﹣1.
18如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°
( ),
∴∠ADC=∠EFC,
∴AD∥ ( ),
∴∠ +∠2=180°( ),
∵∠1+∠2=180°,
∴∠ =∠ ( ),
∴DG∥ ( ),
∴∠CGD=∠CAB.
19疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果很好;B.效果较好;C.效果一般;D.效果不理想),并根据调查结果绘制了如图两幅不完整的统计图:
(1)此次调查中,共抽查了
名学生;
(2)补全条形统计图;
(3)求出扇形统计图中∠α的度数;
(4)根据本次调查情况,请你估计我市某校5000名学生中自我评价为“效果不理想”的人数有多少?
20如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
21周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是
,因变量是
;
(2)小明家到滨海公园的路程为
km,小明在中心书城逗留的时间为
h;
(3)小明出发
小时后爸爸驾车出发;
(4)小明从中心书城到滨海公园的平均速度为
km/h,小明爸爸驾车的平均速度为
km/h;
(5)爸爸驾车经过
小时追上小明,他离家路程s与小明离家时间t之间的关系式为
.
22我们已经学过了对顶角、邻补角、同位角等,知道了它们的特征.现在若有两个角,它们不是同一个顶点,但这两角的两边相互平行,我们就把满足这个条件的两个角称作“平行角”.如图1,已知AB∥CD,AD∥BC,因此∠B和∠D是“平行角”.
(1)图1中,证明∠B=∠D;
(2)如图2,延长DC到E,可知∠A和∠BCE也是“平行角”,判断它们的数量关系;
(3)如图3,DE平分∠ADC,BF平分∠ABC,请说明图中的∠1和∠2是“平行角”.
参考答案与试题解析
一.选择题(共10小题)
1.以下调查方式比较合理的是( )
A.了解全国学生周末使用网络情况,采用普查的方式
B.了解全国七年级学生节约用水的情况,采用抽样调查的方式
C.了解一沓钞票中有没有假钞,采用抽样调查的方式
D.了解全国中学生心理健康现状,采用普查的方式
【分析】根据全面调查和抽样调查的意义,结合实际需要进行判断即可.
【解答】解:A.了解全国学生周末使用网络情况,由于数量较大,且没有必要,因此采用抽样调查的方式较好,因此A不符合题意;
B.了解全国七年级学生节约用水的情况,采用抽样调查的方式较好,因此B符合题意;
C.了解一沓钞票中有没有假钞,必须每一种都要检查,因此采用全面调查的方式较好,因此C不符合题意;
D.了解全国中学生心理健康现状,由于个体较多,且没有必要全面调查,采用抽样调查的方式较好,因此D不符合题意;
故选:B.
2.下列计算正确的是( )
A.
B.(a2)3=a5
C.a﹣1÷a﹣3=a2
D.(a+b)2=a2+b2
【分析】分别根据任何非零数的零次幂等于1,幂的乘方运算法则,同底数幂的乘法法则,负整数指数幂的定义以及完全平方公式逐一判断即可.
【解答】解:A、,故本选项不合题意;
B、(a2)3=a6,故本选项不合题意;
C、a﹣1÷a﹣3=a﹣1+3=a2,故本选项符合题意;
D、(a+b)2=a2+2ab+b2,故本选项不合题意.
故选:C.
3.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1
B.2
C.3
D.4
【分析】总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考察的对象.从而找出总体、个体.
【解答】解:①为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,这种调查采用了抽样调查的方式,故说法正确;
②7万名考生的数学成绩是总体,故原说法错误;
③每名考生的数学成绩是个体,故说法正确;
④1000名考生的数学成绩是总体的一个样本,故说法正确;
⑤1000是样本容量,故原说法错误.
所以正确的说法有3个.
故选:C.
4.根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )
A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
【分析】根据扇形统计图中的百分比的意义逐一判断即可得.
【解答】解:A.扇形统计图能反映各部分在总体中所占的百分比,此选项正确;
B.每天阅读30分钟以上的居民家庭孩子超过50%,此选项正确;
C.每天阅读1小时以上的居民家庭孩子占30%,此选项错误;
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是360°×(1﹣40%﹣20%﹣10%)=108°,此选项正确;
故选:C.
5.如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,则线段CD的长是( )
A.1
B.2
C.3
D.4
【分析】根据已知条件得到BC=8,求得AB=AC+BC=12,由于点D是线段AB的中点,于是得到结论.
【解答】解:∵AC=4,线段BC的长是线段AC长的两倍,
∴BC=8,
∴AB=AC+BC=12,
∵点D是线段AB的中点,
∴AD=AB=6,
∴CD=AD﹣AC=2.
故选:B.
6.在下列图形中,由条件∠1+∠2=180°,不能得到AB∥CD的是( )
A.
B.
C.
D.
【分析】在三线八角的前提下,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.据此判断即可.
【解答】解:A、∠1的对顶角与∠2的对顶角是同旁内角,它们互补,所以能判定AB∥CD,故本选项不符合题意;
B、∠1的对顶角与∠2是同旁内角,它们互补,所以能判定AB∥CD,故本选项不符合题意;
C、∠1的邻补角∠BAD=∠2,所以能判定AB∥CD,故本选项不符合题意;
D、由条件∠1+∠2=180°能得到AD∥BC,不能判定AB∥CD,故本选项符合题意;
故选:D.
7.如图,“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,h表示壶底到水面的高度,下列图象适合表示h与t的对应关系的是( )
A.
B.
C.
D.
【分析】根据题意,可知y随t的增大而减小,符合一次函数图象,从而可以解答本题.
【解答】解:∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度,
∴y随t的增大而减小,符合一次函数图象,
故选:A.
8.如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10°
B.20°
C.30°
D.40°
【分析】根据平角的定义得到∠CEF=180°﹣∠FEA=180°﹣40°=140°,由角平分线的定义可得,由GE⊥EF可得∠GEF=90°,可得∠CEG=180°﹣∠AEF﹣∠GEF=180°﹣40°﹣90°=50°,由∠GEB=∠CEB﹣∠CEG可得结果.
【解答】解:∵∠FEA=40°,GE⊥EF,
∴∠CEF=180°﹣∠FEA=180°﹣40°=140°,∠CEG=180°﹣∠AEF﹣∠GEF=180°﹣40°﹣90°=50°,
∵射线EB平分∠CEF,
∴,
∴∠GEB=∠CEB﹣∠CEG=70°﹣50°=20°,
故选:B.
9.如图,在△ABC中∠ABC=60°,点C在直线b上,若直线a∥b,∠2=26°,则∠1的度数为( )
A.26°
B.28°
C.34°
D.36°
【分析】如图,过点B作BE∥a.想办法证明∠1+∠2=60°即可解决问题.
【解答】解:如图,过点B作BE∥a.
∵a∥b,a∥BE,
∴b∥BE,
∴∠1=∠ABE,∠2=∠CBE,
∵∠ABC=∠ABE+∠CBE=60°,
∴∠1+∠2=60°,
∵∠2=26°,
∴∠1=34°,
故选:C.
10.牛奶配送员小吴从县城出发,骑配送车到米村配送牛奶,途中遇到在县城上学的外甥张聪从米村步行返校上学,小吴在米村配送牛奶后,在返回县城途中又遇到张聪,便用配送车载上张聪一起返回县城,结果小吴比预计时间晚到5分钟,二人与县城间的距离y(km)和小吴从县城出发后所用时间x(min)之间的关系如图,假设两人之间的交流时间忽略不计,则下列说法正确的有( )个.
①小吴到达米村后配送牛奶所用时间为25min;②小吴从县城出发,最后回到县城用时100min;③两人第一次相遇时,小吴距离米村2km;④张聪从米村到县城步行速度为0.05km/min.
A.1
B.2
C.3
D.4
【分析】由图象可知,从35分钟到60分钟,小吴一直在米村配送牛奶,由此可得配送牛奶所用时间,由小吴从离城7千米到2千米用时85分钟,可得小吴返回时的速度,进而可得其从县城出发,最后回到县城用的时间,由两人第一次相遇的时间25分钟可得小吴与米村的距离,分别找到两人两次相遇时,张聪所走的路程和所用的时间,可得其步行速度.
【解答】解:小吴到达米村后配送牛奶所用时间为60﹣35=25(min),故①正确;
从图中可知,小吴从离城7千米到2千米用时85分钟,
∴小吴返回的速度为(7﹣2)÷(85﹣60)=0.2(km/min),
∴小吴原计划返回用时7÷0.2=35(分钟),
∵结果小吴比预计时间晚到5分钟,
∴小吴实际返回用时35+5=40(分钟),
∴小吴从县城出发,最后回到县城用时60+40=100(分钟),故②正确;
由图象可知,小吴35分钟后离县城7千米,
∴两人第一次相遇,即25分钟时小吴距离米村7﹣25×(7÷35)=2(千米),故③正确;
两次相遇时张聪走的路程为5﹣2=3(千米),用时为85﹣25=60(分钟),
∴张聪从米村到县城步行速度为3÷60=0.05(km/min),故④正确.
综上,说法正确的共有4个,
故选:D.
二.填空题(共5小题)
11.冠状病毒最先是1937年从鸡身上分离出来,病毒颗粒的平均直径为0.00000011m,用科学记数法表示这个数是 1.1×10﹣7 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00000011=1.1×10﹣7,
故答案是:1.1×10﹣7.
12.已知a+b=2,ab=﹣7,则(a﹣2)(b﹣2)= ﹣7 .
【分析】将(a﹣2)(b﹣2)变形为ab﹣2(a+b)+4的形式后代入已知条件即可得到答案.
【解答】解:(a﹣2)(b﹣2)
=ab﹣2(a+b)+4
=﹣7﹣2×2+4
=﹣7.
故答案为:﹣7.
13.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D′,C′处,若∠1=56°,则∠EFC的度数是
118° .
【分析】根据折叠性质得出∠DED′=2∠DEF,根据∠1的度数求出∠DED′,即可得出∠DEF,再根据平行线的性质即可求出答案.
【解答】解:由折叠的性质得:∠DED′=2∠DEF,
∵∠1=56°,
∴∠DED′=180°﹣∠1=124°,
∴∠DEF=62°,
∵AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠EFC=118°.
故答案为:118°.
14.如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是 105° .
【分析】过点G作HG∥BC,则有∠HGB=∠B,∠HGE=∠E,又因为△DEF和△ABC都是特殊直角三角形,∠F=30°,∠C=45°,可以得到∠E=60°,∠B=45°,有∠EGB=∠HGE+∠HGB即可得出答案.
【解答】解:过点G作HG∥BC,
∵EF∥BC,
∴GH∥BC∥EF,
∴∠HGB=∠B,∠HGE=∠E,
在Rt△DEF和Rt△ABC中,∠F=30°,∠C=45°,
∴∠E=60°,∠B=45°,
∴∠HGB=∠B=45°,∠HGE=∠E=60°,
∴∠EGB=∠HGE+∠HGB=60°+45°=105°,
故∠EGB的度数是105°,
故答案为:105°.
15.观察如图图形的构成规律,依照此规律,第100个图形中共有 10101 个“?”.
【分析】观察图形可知前4个图形中分别有:3,7,13,21个“?”,所以可得规律为:第n个图形中共有[n(n+1)+1]个“?”,依此即可求解.
【解答】解:由图形可知:
n=1时,“?”的个数为:1×2+1=3,
n=2时,“?”的个数为:2×3+1=7,
n=3时,“?”的个数为:3×4+1=13,
n=4时,“?”的个数为:4×5+1=21,
所以n=n时,“?”的个数为:n(n+1)+1,
n=100时,“?”的个数为:100×(100+1)+1=10101.
故答案为:10101.
三.解答题
16计算:
(1)(﹣a)3?a2﹣(﹣3a3)2÷a.
(2)20212﹣2022×2020.
【考点】同底数幂的乘法;幂的乘方与积的乘方;平方差公式;整式的除法.
【专题】整式;运算能力.
【答案】(1)﹣10a5;
(2)1.
【分析】(1)先计算乘方运算,再计算乘除,最后合并同类项即可;
(2)先利用平方差公式展开,再合并即可得到答案.
【解答】解:(1)原式=﹣a3?a2﹣9a6÷a
=﹣a5﹣9a5
=﹣10a5;
(2)原式=20212﹣(2021+1)×(2021﹣1)
=20212﹣20212+1
=1.
17先化简,再求值:a(a+6)﹣(a+3)(a﹣3)+(2a﹣1)2,其中a=﹣1.
【考点】整式的混合运算—化简求值.
【专题】计算题;整式.
【答案】见试题解答内容
【分析】原式利用单项式乘以多项式,平方差公式,以及完全平方公式计算得到最简结果,把a的值代入计算即可求出值.
【解答】解:原式=a2+6a﹣a2+9+4a2﹣4a+1=4a2+2a+10,
当a=﹣1时,原式=4﹣2+10=12.
18如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°
( ),
∴∠ADC=∠EFC,
∴AD∥ ( ),
∴∠ +∠2=180°( ),
∵∠1+∠2=180°,
∴∠ =∠ ( ),
∴DG∥ ( ),
∴∠CGD=∠CAB.
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】根据同位角相等,两直线平行得出AD∥EF,根据平行线的性质得出∠3+∠2=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
【解答】解:∠CGD=∠CAB,理由如下:
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠3+∠2=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°,
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB.
故答案为:垂直定义;EF;同位角相等,两直线平行;3;两直线平行,同旁内角互补;1;3;同角的补角相等;AB;内错角相等,两直线平行.
19疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果很好;B.效果较好;C.效果一般;D.效果不理想),并根据调查结果绘制了如图两幅不完整的统计图:
(1)此次调查中,共抽查了
名学生;
(2)补全条形统计图;
(3)求出扇形统计图中∠α的度数;
(4)根据本次调查情况,请你估计我市某校5000名学生中自我评价为“效果不理想”的人数有多少?
【考点】抽样调查的可靠性;用样本估计总体;扇形统计图;条形统计图.
【专题】统计与概率;数据分析观念.
【答案】(1)200;(2)补全的条形统计图见解答;(3)72°;(4)500人.
【分析】(1)根据学习效果A的人数和所占的百分比,可以计算出本次调查的人数;
(2)根据(1)中的结果和条形统计图中的数据,可以计算出学习效果C的人数,然后即可将条形统计图补充完整;
(3)根据条形统计图中的数据,可以计算出∠α的度数;
(4)根据条形统计图中的数据,可以计算出我市某校5000名学生中自我评价为“效果不理想”的人数有多少.
【解答】解:(1)此次调查中,共抽查了80÷40%=200名学生,
故答案为:200;
(2)学习效果C的学生有:200﹣80﹣60﹣20=40(人),
补全的条形统计图如右图所示;
(3)∠α=360°×=72°,
即扇形统计图中∠α是72°;
(4)5000×=500(人),
答:估计我市某校5000名学生中自我评价为“效果不理想”的有500人.
20如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
【考点】平行线的判定与性质.
【专题】几何图形.
【答案】见试题解答内容
【分析】(1)根据平行线的判定得出即可.
(2)根据平行线的性质求出∠B.
【解答】解:(1)∵AC∥DE,
∴∠C=∠1,
∵∠AFD=∠1,
∴∠C=∠AFD,
∴DF∥BC.
(2)∵∠1=68°,DF∥BC,
∴∠EDF=∠1=68°,
∵DF平分∠ADE,
∴∠ADF=∠EDF=68°,
∵DF∥BC,
∴∠B=∠ADF=68°.
21周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是
,因变量是
;
(2)小明家到滨海公园的路程为
km,小明在中心书城逗留的时间为
h;
(3)小明出发
小时后爸爸驾车出发;
(4)小明从中心书城到滨海公园的平均速度为
km/h,小明爸爸驾车的平均速度为
km/h;
(5)爸爸驾车经过
小时追上小明,他离家路程s与小明离家时间t之间的关系式为
.
【考点】常量与变量;函数关系式;函数的图象.
【专题】一次函数及其应用;应用意识.
【答案】(1)时间;路程;
(2)30;1.7;
(3)2.5;
(4)12;30;
(5);s=30t﹣75(t≥2.5).
【分析】(1)根据图象进行判断,即可得出自变量与因变量;
(2)根据图象中数据进行计算,即可得到路程与时间;
(3)根据梯形即可得到爸爸驾车出发的时间;
(4)根据相应的路程除以时间,即可得出速度;
(5)根据(4)的结论可得爸爸驾车追上小明的时间,利用待定系数法可得他离家路程s与小明离家时间t之间的关系式.
【解答】解:(1)由图可得,自变量是t,因变量是s,
故答案为:时间,路程;
(2)由图可得,小明家到滨海公园的路程为30km,小明在中心书城逗留的时间为2.5﹣0.8=1.7(h);
故答案为:30,1.7;
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
故答案为:2.5;
(4)小明从中心书城到滨海公园的平均速度为=12(km/h),
小明爸爸驾车的平均速度为=30(km/h);
故答案为:12;30;
(5)爸爸驾车经过h追上小明;
由爸爸的速度为30km/h,可设爸爸离家路程s与小明离家时间t之间的关系式为s=30t+k,
则30=3.5×30+k,
解得k=﹣75;
他离家路程s与小明离家时间t之间的关系式为s=30t﹣75(t≥2.5).
故答案为:;s=30t﹣75(t≥2.5).
22我们已经学过了对顶角、邻补角、同位角等,知道了它们的特征.现在若有两个角,它们不是同一个顶点,但这两角的两边相互平行,我们就把满足这个条件的两个角称作“平行角”.如图1,已知AB∥CD,AD∥BC,因此∠B和∠D是“平行角”.
(1)图1中,证明∠B=∠D;
(2)如图2,延长DC到E,可知∠A和∠BCE也是“平行角”,判断它们的数量关系;
(3)如图3,DE平分∠ADC,BF平分∠ABC,请说明图中的∠1和∠2是“平行角”.
【考点】同位角、内错角、同旁内角;平行线的判定与性质.
【专题】证明题;线段、角、相交线与平行线;推理能力.
【答案】详见解答.
【分析】(1)(2)利用平行线的性质,推理得结论;
(3)要说明∠1和∠2是“平行角”,需说明DE∥BF,可利用角平分线的性质和平行线的性质和判定.
【解答】(1)证明:∵AB∥CD,AD∥BC,
∴∠D+∠A=180°,∠B+∠A=180°.
∴∠B=∠D.
(2)解:由(1)知∠B=∠D,
同理可得,∠A=∠BCD.
∵∠BCD+∠BCE=180°,
∴∠A+∠BCE=180°.
即∠A和∠BCE互补.
(3)证明:∵∠B和∠D是“平行角”,
∴∠ABC=∠ADC.
∵DE平分∠ADC,BF平分∠ABC
∴∠1=∠ADC,∠2=∠ABC.
∴∠1=∠2.
又∵AB∥DC,
∴∠2=∠BFC.
∴∠1=∠BFC.
∴DE∥BF.
∴∠1和∠2是“平行角”.
一.选择题(本大题满分30分,每小题3分)
1.以下调查方式比较合理的是( )
A.了解全国学生周末使用网络情况,采用普查的方式
B.了解全国七年级学生节约用水的情况,采用抽样调查的方式
C.了解一沓钞票中有没有假钞,采用抽样调查的方式
D.了解全国中学生心理健康现状,采用普查的方式
2.下列计算正确的是( )
A.
B.(a2)3=a5
C.a﹣1÷a﹣3=a2
D.(a+b)2=a2+b2
3.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1
B.2
C.3
D.4
4.根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )
A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
5.如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,则线段CD的长是( )
A.1
B.2
C.3
D.4
6.在下列图形中,由条件∠1+∠2=180°,不能得到AB∥CD的是( )
A.
B.
C.
D.
7.如图,“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,h表示壶底到水面的高度,下列图象适合表示h与t的对应关系的是( )
A.
B.
C.
D.
8.如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10°
B.20°
C.30°
D.40°
9.如图,在△ABC中∠ABC=60°,点C在直线b上,若直线a∥b,∠2=26°,则∠1的度数为( )
A.26°
B.28°
C.34°
D.36°
10.牛奶配送员小吴从县城出发,骑配送车到米村配送牛奶,途中遇到在县城上学的外甥张聪从米村步行返校上学,小吴在米村配送牛奶后,在返回县城途中又遇到张聪,便用配送车载上张聪一起返回县城,结果小吴比预计时间晚到5分钟,二人与县城间的距离y(km)和小吴从县城出发后所用时间x(min)之间的关系如图,假设两人之间的交流时间忽略不计,则下列说法正确的有( )个.
①小吴到达米村后配送牛奶所用时间为25min;②小吴从县城出发,最后回到县城用时100min;③两人第一次相遇时,小吴距离米村2km;④张聪从米村到县城步行速度为0.05km/min.
A.1
B.2
C.3
D.4
二.填空题(本大题满分15分,每小题3分)
11.冠状病毒最先是1937年从鸡身上分离出来,病毒颗粒的平均直径为0.00000011m,用科学记数法表示这个数是
.
12.已知a+b=2,ab=﹣7,则(a﹣2)(b﹣2)=
.
13.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D′,C′处,若∠1=56°,则∠EFC的度数是
.
14.如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是
.
15.观察如图图形的构成规律,依照此规律,第100个图形中共有
个“?”.
三.解答题(本大题满分35分,解答题写出必要的文字说明或推演步骤)
16计算:
(1)(﹣a)3?a2﹣(﹣3a3)2÷a.
(2)20212﹣2022×2020.
17先化简,再求值:a(a+6)﹣(a+3)(a﹣3)+(2a﹣1)2,其中a=﹣1.
18如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°
( ),
∴∠ADC=∠EFC,
∴AD∥ ( ),
∴∠ +∠2=180°( ),
∵∠1+∠2=180°,
∴∠ =∠ ( ),
∴DG∥ ( ),
∴∠CGD=∠CAB.
19疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果很好;B.效果较好;C.效果一般;D.效果不理想),并根据调查结果绘制了如图两幅不完整的统计图:
(1)此次调查中,共抽查了
名学生;
(2)补全条形统计图;
(3)求出扇形统计图中∠α的度数;
(4)根据本次调查情况,请你估计我市某校5000名学生中自我评价为“效果不理想”的人数有多少?
20如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
21周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是
,因变量是
;
(2)小明家到滨海公园的路程为
km,小明在中心书城逗留的时间为
h;
(3)小明出发
小时后爸爸驾车出发;
(4)小明从中心书城到滨海公园的平均速度为
km/h,小明爸爸驾车的平均速度为
km/h;
(5)爸爸驾车经过
小时追上小明,他离家路程s与小明离家时间t之间的关系式为
.
22我们已经学过了对顶角、邻补角、同位角等,知道了它们的特征.现在若有两个角,它们不是同一个顶点,但这两角的两边相互平行,我们就把满足这个条件的两个角称作“平行角”.如图1,已知AB∥CD,AD∥BC,因此∠B和∠D是“平行角”.
(1)图1中,证明∠B=∠D;
(2)如图2,延长DC到E,可知∠A和∠BCE也是“平行角”,判断它们的数量关系;
(3)如图3,DE平分∠ADC,BF平分∠ABC,请说明图中的∠1和∠2是“平行角”.
参考答案与试题解析
一.选择题(共10小题)
1.以下调查方式比较合理的是( )
A.了解全国学生周末使用网络情况,采用普查的方式
B.了解全国七年级学生节约用水的情况,采用抽样调查的方式
C.了解一沓钞票中有没有假钞,采用抽样调查的方式
D.了解全国中学生心理健康现状,采用普查的方式
【分析】根据全面调查和抽样调查的意义,结合实际需要进行判断即可.
【解答】解:A.了解全国学生周末使用网络情况,由于数量较大,且没有必要,因此采用抽样调查的方式较好,因此A不符合题意;
B.了解全国七年级学生节约用水的情况,采用抽样调查的方式较好,因此B符合题意;
C.了解一沓钞票中有没有假钞,必须每一种都要检查,因此采用全面调查的方式较好,因此C不符合题意;
D.了解全国中学生心理健康现状,由于个体较多,且没有必要全面调查,采用抽样调查的方式较好,因此D不符合题意;
故选:B.
2.下列计算正确的是( )
A.
B.(a2)3=a5
C.a﹣1÷a﹣3=a2
D.(a+b)2=a2+b2
【分析】分别根据任何非零数的零次幂等于1,幂的乘方运算法则,同底数幂的乘法法则,负整数指数幂的定义以及完全平方公式逐一判断即可.
【解答】解:A、,故本选项不合题意;
B、(a2)3=a6,故本选项不合题意;
C、a﹣1÷a﹣3=a﹣1+3=a2,故本选项符合题意;
D、(a+b)2=a2+2ab+b2,故本选项不合题意.
故选:C.
3.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1
B.2
C.3
D.4
【分析】总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考察的对象.从而找出总体、个体.
【解答】解:①为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,这种调查采用了抽样调查的方式,故说法正确;
②7万名考生的数学成绩是总体,故原说法错误;
③每名考生的数学成绩是个体,故说法正确;
④1000名考生的数学成绩是总体的一个样本,故说法正确;
⑤1000是样本容量,故原说法错误.
所以正确的说法有3个.
故选:C.
4.根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )
A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
【分析】根据扇形统计图中的百分比的意义逐一判断即可得.
【解答】解:A.扇形统计图能反映各部分在总体中所占的百分比,此选项正确;
B.每天阅读30分钟以上的居民家庭孩子超过50%,此选项正确;
C.每天阅读1小时以上的居民家庭孩子占30%,此选项错误;
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是360°×(1﹣40%﹣20%﹣10%)=108°,此选项正确;
故选:C.
5.如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,则线段CD的长是( )
A.1
B.2
C.3
D.4
【分析】根据已知条件得到BC=8,求得AB=AC+BC=12,由于点D是线段AB的中点,于是得到结论.
【解答】解:∵AC=4,线段BC的长是线段AC长的两倍,
∴BC=8,
∴AB=AC+BC=12,
∵点D是线段AB的中点,
∴AD=AB=6,
∴CD=AD﹣AC=2.
故选:B.
6.在下列图形中,由条件∠1+∠2=180°,不能得到AB∥CD的是( )
A.
B.
C.
D.
【分析】在三线八角的前提下,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.据此判断即可.
【解答】解:A、∠1的对顶角与∠2的对顶角是同旁内角,它们互补,所以能判定AB∥CD,故本选项不符合题意;
B、∠1的对顶角与∠2是同旁内角,它们互补,所以能判定AB∥CD,故本选项不符合题意;
C、∠1的邻补角∠BAD=∠2,所以能判定AB∥CD,故本选项不符合题意;
D、由条件∠1+∠2=180°能得到AD∥BC,不能判定AB∥CD,故本选项符合题意;
故选:D.
7.如图,“漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,h表示壶底到水面的高度,下列图象适合表示h与t的对应关系的是( )
A.
B.
C.
D.
【分析】根据题意,可知y随t的增大而减小,符合一次函数图象,从而可以解答本题.
【解答】解:∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度,
∴y随t的增大而减小,符合一次函数图象,
故选:A.
8.如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10°
B.20°
C.30°
D.40°
【分析】根据平角的定义得到∠CEF=180°﹣∠FEA=180°﹣40°=140°,由角平分线的定义可得,由GE⊥EF可得∠GEF=90°,可得∠CEG=180°﹣∠AEF﹣∠GEF=180°﹣40°﹣90°=50°,由∠GEB=∠CEB﹣∠CEG可得结果.
【解答】解:∵∠FEA=40°,GE⊥EF,
∴∠CEF=180°﹣∠FEA=180°﹣40°=140°,∠CEG=180°﹣∠AEF﹣∠GEF=180°﹣40°﹣90°=50°,
∵射线EB平分∠CEF,
∴,
∴∠GEB=∠CEB﹣∠CEG=70°﹣50°=20°,
故选:B.
9.如图,在△ABC中∠ABC=60°,点C在直线b上,若直线a∥b,∠2=26°,则∠1的度数为( )
A.26°
B.28°
C.34°
D.36°
【分析】如图,过点B作BE∥a.想办法证明∠1+∠2=60°即可解决问题.
【解答】解:如图,过点B作BE∥a.
∵a∥b,a∥BE,
∴b∥BE,
∴∠1=∠ABE,∠2=∠CBE,
∵∠ABC=∠ABE+∠CBE=60°,
∴∠1+∠2=60°,
∵∠2=26°,
∴∠1=34°,
故选:C.
10.牛奶配送员小吴从县城出发,骑配送车到米村配送牛奶,途中遇到在县城上学的外甥张聪从米村步行返校上学,小吴在米村配送牛奶后,在返回县城途中又遇到张聪,便用配送车载上张聪一起返回县城,结果小吴比预计时间晚到5分钟,二人与县城间的距离y(km)和小吴从县城出发后所用时间x(min)之间的关系如图,假设两人之间的交流时间忽略不计,则下列说法正确的有( )个.
①小吴到达米村后配送牛奶所用时间为25min;②小吴从县城出发,最后回到县城用时100min;③两人第一次相遇时,小吴距离米村2km;④张聪从米村到县城步行速度为0.05km/min.
A.1
B.2
C.3
D.4
【分析】由图象可知,从35分钟到60分钟,小吴一直在米村配送牛奶,由此可得配送牛奶所用时间,由小吴从离城7千米到2千米用时85分钟,可得小吴返回时的速度,进而可得其从县城出发,最后回到县城用的时间,由两人第一次相遇的时间25分钟可得小吴与米村的距离,分别找到两人两次相遇时,张聪所走的路程和所用的时间,可得其步行速度.
【解答】解:小吴到达米村后配送牛奶所用时间为60﹣35=25(min),故①正确;
从图中可知,小吴从离城7千米到2千米用时85分钟,
∴小吴返回的速度为(7﹣2)÷(85﹣60)=0.2(km/min),
∴小吴原计划返回用时7÷0.2=35(分钟),
∵结果小吴比预计时间晚到5分钟,
∴小吴实际返回用时35+5=40(分钟),
∴小吴从县城出发,最后回到县城用时60+40=100(分钟),故②正确;
由图象可知,小吴35分钟后离县城7千米,
∴两人第一次相遇,即25分钟时小吴距离米村7﹣25×(7÷35)=2(千米),故③正确;
两次相遇时张聪走的路程为5﹣2=3(千米),用时为85﹣25=60(分钟),
∴张聪从米村到县城步行速度为3÷60=0.05(km/min),故④正确.
综上,说法正确的共有4个,
故选:D.
二.填空题(共5小题)
11.冠状病毒最先是1937年从鸡身上分离出来,病毒颗粒的平均直径为0.00000011m,用科学记数法表示这个数是 1.1×10﹣7 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00000011=1.1×10﹣7,
故答案是:1.1×10﹣7.
12.已知a+b=2,ab=﹣7,则(a﹣2)(b﹣2)= ﹣7 .
【分析】将(a﹣2)(b﹣2)变形为ab﹣2(a+b)+4的形式后代入已知条件即可得到答案.
【解答】解:(a﹣2)(b﹣2)
=ab﹣2(a+b)+4
=﹣7﹣2×2+4
=﹣7.
故答案为:﹣7.
13.如图,将一张长方形纸片ABCD沿EF折叠,点D,C分别落在点D′,C′处,若∠1=56°,则∠EFC的度数是
118° .
【分析】根据折叠性质得出∠DED′=2∠DEF,根据∠1的度数求出∠DED′,即可得出∠DEF,再根据平行线的性质即可求出答案.
【解答】解:由折叠的性质得:∠DED′=2∠DEF,
∵∠1=56°,
∴∠DED′=180°﹣∠1=124°,
∴∠DEF=62°,
∵AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠EFC=118°.
故答案为:118°.
14.如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是 105° .
【分析】过点G作HG∥BC,则有∠HGB=∠B,∠HGE=∠E,又因为△DEF和△ABC都是特殊直角三角形,∠F=30°,∠C=45°,可以得到∠E=60°,∠B=45°,有∠EGB=∠HGE+∠HGB即可得出答案.
【解答】解:过点G作HG∥BC,
∵EF∥BC,
∴GH∥BC∥EF,
∴∠HGB=∠B,∠HGE=∠E,
在Rt△DEF和Rt△ABC中,∠F=30°,∠C=45°,
∴∠E=60°,∠B=45°,
∴∠HGB=∠B=45°,∠HGE=∠E=60°,
∴∠EGB=∠HGE+∠HGB=60°+45°=105°,
故∠EGB的度数是105°,
故答案为:105°.
15.观察如图图形的构成规律,依照此规律,第100个图形中共有 10101 个“?”.
【分析】观察图形可知前4个图形中分别有:3,7,13,21个“?”,所以可得规律为:第n个图形中共有[n(n+1)+1]个“?”,依此即可求解.
【解答】解:由图形可知:
n=1时,“?”的个数为:1×2+1=3,
n=2时,“?”的个数为:2×3+1=7,
n=3时,“?”的个数为:3×4+1=13,
n=4时,“?”的个数为:4×5+1=21,
所以n=n时,“?”的个数为:n(n+1)+1,
n=100时,“?”的个数为:100×(100+1)+1=10101.
故答案为:10101.
三.解答题
16计算:
(1)(﹣a)3?a2﹣(﹣3a3)2÷a.
(2)20212﹣2022×2020.
【考点】同底数幂的乘法;幂的乘方与积的乘方;平方差公式;整式的除法.
【专题】整式;运算能力.
【答案】(1)﹣10a5;
(2)1.
【分析】(1)先计算乘方运算,再计算乘除,最后合并同类项即可;
(2)先利用平方差公式展开,再合并即可得到答案.
【解答】解:(1)原式=﹣a3?a2﹣9a6÷a
=﹣a5﹣9a5
=﹣10a5;
(2)原式=20212﹣(2021+1)×(2021﹣1)
=20212﹣20212+1
=1.
17先化简,再求值:a(a+6)﹣(a+3)(a﹣3)+(2a﹣1)2,其中a=﹣1.
【考点】整式的混合运算—化简求值.
【专题】计算题;整式.
【答案】见试题解答内容
【分析】原式利用单项式乘以多项式,平方差公式,以及完全平方公式计算得到最简结果,把a的值代入计算即可求出值.
【解答】解:原式=a2+6a﹣a2+9+4a2﹣4a+1=4a2+2a+10,
当a=﹣1时,原式=4﹣2+10=12.
18如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°
( ),
∴∠ADC=∠EFC,
∴AD∥ ( ),
∴∠ +∠2=180°( ),
∵∠1+∠2=180°,
∴∠ =∠ ( ),
∴DG∥ ( ),
∴∠CGD=∠CAB.
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】根据同位角相等,两直线平行得出AD∥EF,根据平行线的性质得出∠3+∠2=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
【解答】解:∠CGD=∠CAB,理由如下:
∵AD⊥BC,EF⊥BC,
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠3+∠2=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°,
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB.
故答案为:垂直定义;EF;同位角相等,两直线平行;3;两直线平行,同旁内角互补;1;3;同角的补角相等;AB;内错角相等,两直线平行.
19疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果很好;B.效果较好;C.效果一般;D.效果不理想),并根据调查结果绘制了如图两幅不完整的统计图:
(1)此次调查中,共抽查了
名学生;
(2)补全条形统计图;
(3)求出扇形统计图中∠α的度数;
(4)根据本次调查情况,请你估计我市某校5000名学生中自我评价为“效果不理想”的人数有多少?
【考点】抽样调查的可靠性;用样本估计总体;扇形统计图;条形统计图.
【专题】统计与概率;数据分析观念.
【答案】(1)200;(2)补全的条形统计图见解答;(3)72°;(4)500人.
【分析】(1)根据学习效果A的人数和所占的百分比,可以计算出本次调查的人数;
(2)根据(1)中的结果和条形统计图中的数据,可以计算出学习效果C的人数,然后即可将条形统计图补充完整;
(3)根据条形统计图中的数据,可以计算出∠α的度数;
(4)根据条形统计图中的数据,可以计算出我市某校5000名学生中自我评价为“效果不理想”的人数有多少.
【解答】解:(1)此次调查中,共抽查了80÷40%=200名学生,
故答案为:200;
(2)学习效果C的学生有:200﹣80﹣60﹣20=40(人),
补全的条形统计图如右图所示;
(3)∠α=360°×=72°,
即扇形统计图中∠α是72°;
(4)5000×=500(人),
答:估计我市某校5000名学生中自我评价为“效果不理想”的有500人.
20如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
【考点】平行线的判定与性质.
【专题】几何图形.
【答案】见试题解答内容
【分析】(1)根据平行线的判定得出即可.
(2)根据平行线的性质求出∠B.
【解答】解:(1)∵AC∥DE,
∴∠C=∠1,
∵∠AFD=∠1,
∴∠C=∠AFD,
∴DF∥BC.
(2)∵∠1=68°,DF∥BC,
∴∠EDF=∠1=68°,
∵DF平分∠ADE,
∴∠ADF=∠EDF=68°,
∵DF∥BC,
∴∠B=∠ADF=68°.
21周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是
,因变量是
;
(2)小明家到滨海公园的路程为
km,小明在中心书城逗留的时间为
h;
(3)小明出发
小时后爸爸驾车出发;
(4)小明从中心书城到滨海公园的平均速度为
km/h,小明爸爸驾车的平均速度为
km/h;
(5)爸爸驾车经过
小时追上小明,他离家路程s与小明离家时间t之间的关系式为
.
【考点】常量与变量;函数关系式;函数的图象.
【专题】一次函数及其应用;应用意识.
【答案】(1)时间;路程;
(2)30;1.7;
(3)2.5;
(4)12;30;
(5);s=30t﹣75(t≥2.5).
【分析】(1)根据图象进行判断,即可得出自变量与因变量;
(2)根据图象中数据进行计算,即可得到路程与时间;
(3)根据梯形即可得到爸爸驾车出发的时间;
(4)根据相应的路程除以时间,即可得出速度;
(5)根据(4)的结论可得爸爸驾车追上小明的时间,利用待定系数法可得他离家路程s与小明离家时间t之间的关系式.
【解答】解:(1)由图可得,自变量是t,因变量是s,
故答案为:时间,路程;
(2)由图可得,小明家到滨海公园的路程为30km,小明在中心书城逗留的时间为2.5﹣0.8=1.7(h);
故答案为:30,1.7;
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
故答案为:2.5;
(4)小明从中心书城到滨海公园的平均速度为=12(km/h),
小明爸爸驾车的平均速度为=30(km/h);
故答案为:12;30;
(5)爸爸驾车经过h追上小明;
由爸爸的速度为30km/h,可设爸爸离家路程s与小明离家时间t之间的关系式为s=30t+k,
则30=3.5×30+k,
解得k=﹣75;
他离家路程s与小明离家时间t之间的关系式为s=30t﹣75(t≥2.5).
故答案为:;s=30t﹣75(t≥2.5).
22我们已经学过了对顶角、邻补角、同位角等,知道了它们的特征.现在若有两个角,它们不是同一个顶点,但这两角的两边相互平行,我们就把满足这个条件的两个角称作“平行角”.如图1,已知AB∥CD,AD∥BC,因此∠B和∠D是“平行角”.
(1)图1中,证明∠B=∠D;
(2)如图2,延长DC到E,可知∠A和∠BCE也是“平行角”,判断它们的数量关系;
(3)如图3,DE平分∠ADC,BF平分∠ABC,请说明图中的∠1和∠2是“平行角”.
【考点】同位角、内错角、同旁内角;平行线的判定与性质.
【专题】证明题;线段、角、相交线与平行线;推理能力.
【答案】详见解答.
【分析】(1)(2)利用平行线的性质,推理得结论;
(3)要说明∠1和∠2是“平行角”,需说明DE∥BF,可利用角平分线的性质和平行线的性质和判定.
【解答】(1)证明:∵AB∥CD,AD∥BC,
∴∠D+∠A=180°,∠B+∠A=180°.
∴∠B=∠D.
(2)解:由(1)知∠B=∠D,
同理可得,∠A=∠BCD.
∵∠BCD+∠BCE=180°,
∴∠A+∠BCE=180°.
即∠A和∠BCE互补.
(3)证明:∵∠B和∠D是“平行角”,
∴∠ABC=∠ADC.
∵DE平分∠ADC,BF平分∠ABC
∴∠1=∠ADC,∠2=∠ABC.
∴∠1=∠2.
又∵AB∥DC,
∴∠2=∠BFC.
∴∠1=∠BFC.
∴DE∥BF.
∴∠1和∠2是“平行角”.
同课章节目录
