山东省泰安市东平县2020-2021学年六年级下学期期末数学试卷(五四学制)(word解析版)
文档属性
| 名称 | 山东省泰安市东平县2020-2021学年六年级下学期期末数学试卷(五四学制)(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 21:03:32 | ||
图片预览



文档简介
2020-2021学年山东省泰安市东平县六年级(下)期末数学试卷(五四学制)
一、选择题(本大题共12个小题,每小题4分,共48分.每小题给出的四个答案中,只有一项是正确的.)
1.平面上有四点,经过其中的两点画直线最多可画出( )
A.三条
B.四条
C.五条
D.六条
2.下列运算正确的是( )
A.a2+a2=a4
B.a3?a4=a12
C.(a3)4=a12
D.(ab)2=ab2
3.生物学家发现了一种病毒,其长度约为0.00000032mm,它的1%用科学记数法表示正确的是( )
A.3.2×10﹣10
B.3.2×10﹣8
C.3.2×10﹣7
D.3.2×10﹣9
4.中学生骑电动车上学给交通安全带来隐患,为了解某中学2500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A.该校约有90%的家长持反对态度
B.调查方式是普查
C.该校只有360个家长持反对态度
D.样本是360个家长
5.下列说法中,正确的个数是( )
(1)过两点有且只有一条线段;
(2)连接两点的线段的长度叫做两点的距离:
(3)两点之间,线段最短;
(4)AB=BC,则点B是线段AC的中点;
(5)射线比直线短.
A.1
B.2
C.3
D.4
6.如图直线l1∥l2,AB⊥CD,∠1=34°,那么∠2的度数是( )
A.34°
B.56°
C.46°
D.44°
7.如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠A=180°,所以BC∥AD.
A.1个
B.2个
C.3个
D.4个
8.如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
A.5°
B.10°
C.15°
D.20°
9.已知∠A=40°,则∠A的余角的补角是( )
A.130°
B.120°
C.50°
D.60°
10.过多边形的一条边(不含顶点)上的一个点向各顶点连线,可将此多边形分成7个三角形,则此多边形的边数为( )
A.6
B.7
C.8
D.9
11.如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )
A.垂直
B.相交
C.平行
D.不能确定
12.正方形边长为5厘米,若边长减少x,则面积减少y.下列说法正确的是( )
A.边长x是自变量,面积减少量y是因变量
B.边长是自变量,面积是因变量
C.上述关系式为y=(5﹣x)2
D.上述关系式为y=52﹣(5﹣x)2
二、填空题(本大题共8小题,每小题4分,共32分.只要求填写最后结果)
13.若m2﹣2km+是关于m的完全平方式,则k的值是
.
14.一个人从A地出发沿北偏东60°方向走到B地,再从B地出发沿南偏西20°方向走到C地,那么∠ABC=
度.
15.如图所示,将长方形纸片ABCD进行折叠,如果∠BHG=70°,那么∠BHE=
度.
16.如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP与∠EFP的平分线相交于点P,且∠EFD=60°,EP⊥FP,则∠BEP=
度.
17.如图,已知AB和CD的公共部分BD=AB=CD,线段AB,CD的中点E,F之间的距离是10cm,则AB的长是
.
18.线段AB=5cm,点C在直线AB上,BC=3cm,则线段AC的一半是
.
19九点45分时,钟面上的时针与分针的夹角是
度.
20若a2+b2=5,ab=2,则(a+b)2= .
三、解答题(本大题共7小题,共70分写出必要的文字说明、证明过程或推演步骤)
21计算:
(1)(x﹣2y+1)(x+2y﹣1)﹣(x+2y+1)(x﹣2y﹣1);
(2)[(x﹣3y)(x+3y)+(3y﹣x)2]÷(﹣2x).
22先化简,再求值:(x﹣y2)﹣(x﹣y)(x+y)+(x+y)2,其中x2﹣2x+1+(y+3)2=0.
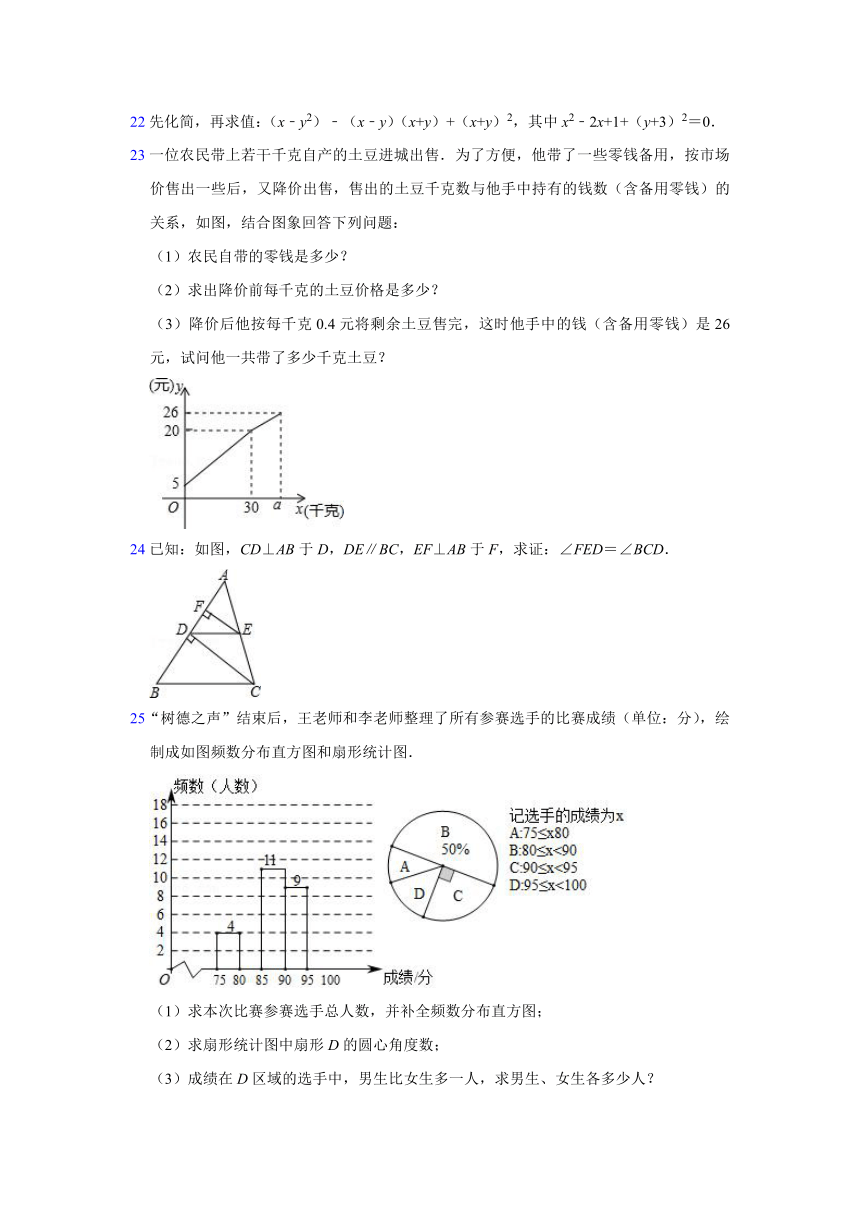
23一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
24已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.
25“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数分布直方图和扇形统计图.
(1)求本次比赛参赛选手总人数,并补全频数分布直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,求男生、女生各多少人?
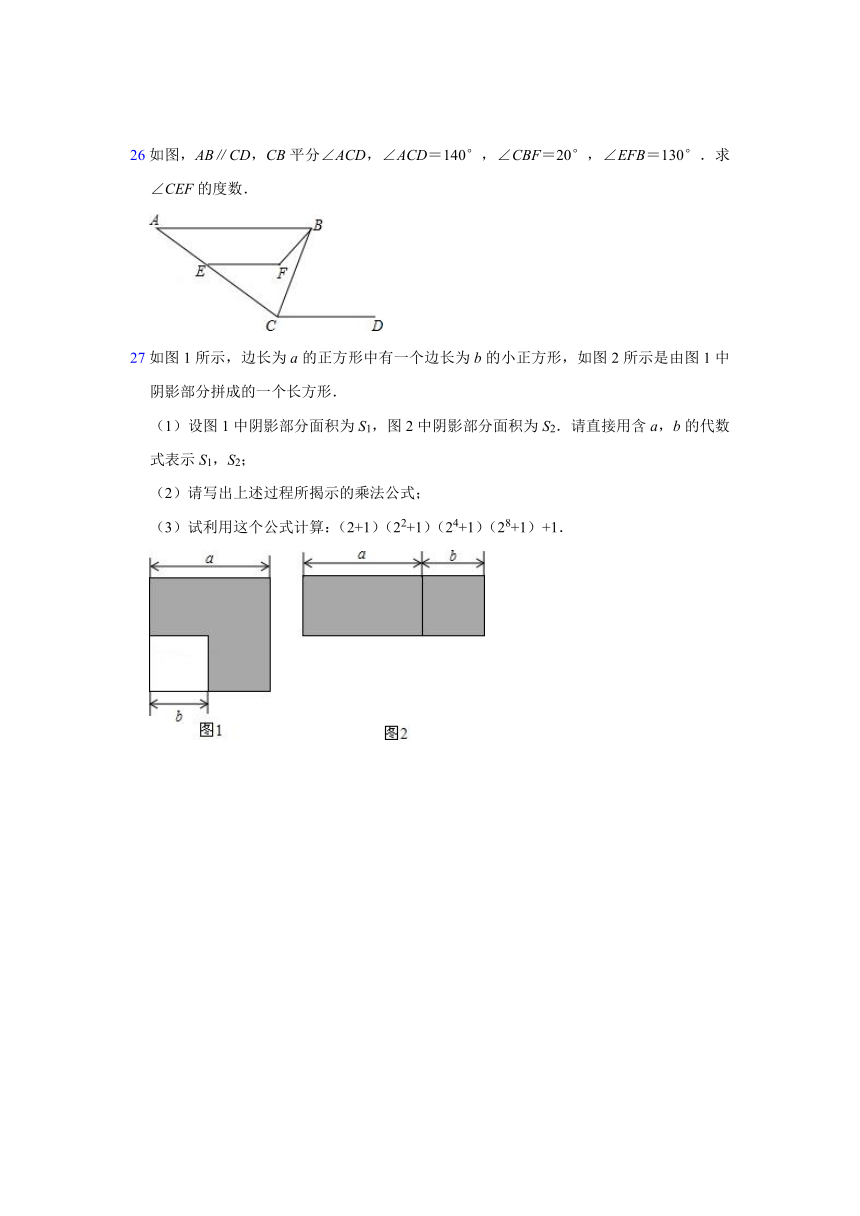
26如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
27如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个长方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
参考答案与试题解析
一.选择题(共12小题)
1.平面上有四点,经过其中的两点画直线最多可画出( )
A.三条
B.四条
C.五条
D.六条
【分析】画出图形即可确定最多能画的直线的条数.
【解答】解:如图,最多可画6条直线.
,
故选:D.
2.下列运算正确的是( )
A.a2+a2=a4
B.a3?a4=a12
C.(a3)4=a12
D.(ab)2=ab2
【分析】分别根据合并同类项的法则、同底数幂的乘法、幂的乘方以及积的乘方化简即可判断.
【解答】解:A.a2+a2=2a2,故选项A不合题意;
B.a3?a4=a7,故选项B不合题意;
C.(a3)4=a12,故选项C符合题意;
D.(ab)2=a2b2,故选项D不合题意.
故选:C.
3.生物学家发现了一种病毒,其长度约为0.00000032mm,它的1%用科学记数法表示正确的是( )
A.3.2×10﹣10
B.3.2×10﹣8
C.3.2×10﹣7
D.3.2×10﹣9
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00000032×1%=0.0000000032=3.2×10﹣9.
故选:D.
4.中学生骑电动车上学给交通安全带来隐患,为了解某中学2500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A.该校约有90%的家长持反对态度
B.调查方式是普查
C.该校只有360个家长持反对态度
D.样本是360个家长
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:A.该校约有90%的家长持反对态度,说法正确,故本选项符合题意;
B.调查方式是抽样调查,故本选项不合题意;
C.该校有2250个家长持反对态度,故本选项不合题意;
D.样本是400个家长对“中学生骑电动车上学”的态度,故本选项不合题意;
故选:A.
5.下列说法中,正确的个数是( )
(1)过两点有且只有一条线段;
(2)连接两点的线段的长度叫做两点的距离:
(3)两点之间,线段最短;
(4)AB=BC,则点B是线段AC的中点;
(5)射线比直线短.
A.1
B.2
C.3
D.4
【分析】根据直线,线段的性质,两点间距离的定义,对各小题分析判断后利用排除法求解.
【解答】解:(1过两点有且只有一条线段,错误;
(2)应为连接两点的线段的长度叫做两点的距离,故本小题正确:
(3)两点之间,线段最短,正确;
(4)AB=BC,则点B是线段AC的中点,错误,因为A、B、C三点不一定在同一直线上,故本小题错误;
(5)射线比直线短,错误,射线与直线不能比较长短,故本小题错误.
综上所述,正确的有(2)(3)共2个.
故选:B.
6.如图直线l1∥l2,AB⊥CD,∠1=34°,那么∠2的度数是( )
A.34°
B.56°
C.46°
D.44°
【分析】根据垂直的定义得到∠4=90°,根据三角形外角性质有∠4=∠1+∠3,则∠3=90°﹣∠1=90°﹣34°=56°,由l1∥l2,根据两直线平行,同位角相等即可得到∠2=∠3=56°.
【解答】解:如图:
∵AB⊥CD,
∴∠4=90°,
∵∠4=∠1+∠3,∠1=34°,
∴∠3=90°﹣∠1=90°﹣34°=56°,
∵l1∥l2,
∴∠2=∠3=56°.
故选:B.
7.如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠A=180°,所以BC∥AD.
A.1个
B.2个
C.3个
D.4个
【分析】根据平行线的判定定理判断求解即可.
【解答】解:∵∠1=∠4,
∴AB∥CD,
故①错误,不符合题意;
∵∠2=∠3,
∴BC∥AD,
故②错误,不符合题意;
∵∠BCD+∠ADC=180°,
∴AD∥BC,
故③正确,符合题意;
∵∠1+∠2+∠A=180°,
即∠ABC+∠A=180°,
∴BC∥AD,
故④正确,符合题意;
故推理符合题意的有2个,
故选:B.
8.如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
A.5°
B.10°
C.15°
D.20°
【分析】利用角平分线得到∠AOB=∠BOD=2∠BOC,借助图形即可求出∠BOC.
【解答】解:∵OC平分∠BOD,
∴∠BOD=2∠BOC,
∵OB平分∠AOD,
∴∠AOB=∠BOD=2∠BOC,
∵∠AOC=45°,
∴∠AOC=∠AOB+∠BOC=2∠BOC+∠BOC=3∠BOC=45°,
∴∠BOC=∠AOC=15°,
故选:C.
9.已知∠A=40°,则∠A的余角的补角是( )
A.130°
B.120°
C.50°
D.60°
【分析】先计算出∠A的余角,再计算出它余角的补角.
【解答】解:因为∠A=40°,
所以∠A的余角就是:90°﹣40°=50°.
而∠A的余角的补角就是:180°﹣50°=130°.
故选:A.
10.过多边形的一条边(不含顶点)上的一个点向各顶点连线,可将此多边形分成7个三角形,则此多边形的边数为( )
A.6
B.7
C.8
D.9
【分析】若P点取在一边上(不含顶点),则可以与其他顶点连接出(n﹣2)条线段,可以分n边形为(n﹣1)个三角形.
【解答】解:此多边形的边数为:7+1=8.
故选:C.
11.如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )
A.垂直
B.相交
C.平行
D.不能确定
【分析】由两条平行线被第三条直线所截,根据两直线平行,同位角相等,即可得一组同位角相等即∠FEB=∠GFD,又由角平分线的性质求得∠1=∠2,然后根据同位角相等,两直线平行,即可求得答案.
【解答】解:∵AB∥CD,
∴∠FEB=∠GFD,
∵EM与FN分别是∠FEM与∠GFD的平分线,
∴∠1=∠FEB,∠2=∠GFD,
∴∠1=∠2,
∴EM∥FN.
故选:C.
12.正方形边长为5厘米,若边长减少x,则面积减少y.下列说法正确的是( )
A.边长x是自变量,面积减少量y是因变量
B.边长是自变量,面积是因变量
C.上述关系式为y=(5﹣x)2
D.上述关系式为y=52﹣(5﹣x)2
【分析】根据题意可得减小后的边长及减小后的面积,进而可得面积的减小量y与x的关系式,由此可判断C,D选项;结合函数关系式根据自变量和因变量的概念可判断A,B选项.
【解答】解:由题意得边长减小为5﹣x,减小后的面积为(5﹣x)2,
∴y与x的关系式为y=52﹣(5﹣x)2;
由因变量和自变量的概念可知:x是自变量,y是因变量,即边长减小量为自变量,面积减少量是因变量,
故选:D.
二.填空题(共6小题)
13.若m2﹣2km+是关于m的完全平方式,则k的值是
﹣或 .
【分析】根据完全平方式得出﹣2k=±2×,再求出即可.
【解答】解:∵m2﹣2km+是关于m的完全平方式,
∴﹣2k=±2×,
解得:k=﹣或,
故答案为:﹣或.
14.一个人从A地出发沿北偏东60°方向走到B地,再从B地出发沿南偏西20°方向走到C地,那么∠ABC= 40 度.
【分析】根据方位角的概念,画图正确表示出行驶的过程,再根据已知转向的角度结合三角形的内角和与外角的关系求解.
【解答】解:如图,A沿北偏东60°的方向行驶到B,则∠BAC=90°﹣60°=30°,
B沿南偏西20°的方向行驶到C,则∠BCO=90°﹣20°=70°,
又∵∠ABC=∠BCO﹣∠BAC,
∴∠ABC=70°﹣30°=40°.
故答案为:40.
15.如图所示,将长方形纸片ABCD进行折叠,如果∠BHG=70°,那么∠BHE= 55 度.
【分析】利用平行线的性质可得∠1=70°,利用折叠及平行线的性质,三角形的内角和定理可得所求角的度数.
【解答】解:由题意得EF∥GH,
∴∠1=∠BHG=70°,
∴∠FEH+∠BHE=110°,
由折叠可得∠2=∠FEH,
∵AD∥BC
∴∠2=∠BHE,
∴∠FEH=∠BHE=55°.
故答案为55.
16.如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP与∠EFP的平分线相交于点P,且∠EFD=60°,EP⊥FP,则∠BEP= 60 度.
【分析】根据平行线的性质和角平分线的定义求解.
【解答】解:∵AB∥CD,
∴∠BEF=180﹣∠EFD=120°;
∵FP平分∠EFD,且∠EFD=60°,
∴∠EFP=30°,
在△EFP中,EP⊥FP,
∴∠FEP=60°;
∴∠BEP=∠BEF﹣∠FEP=60°,
故答案为:60.
17.如图,已知AB和CD的公共部分BD=AB=CD,线段AB,CD的中点E,F之间的距离是10cm,则AB的长是
cm .
【分析】设BD=x,则AB=3x,CD=4x,由中点的定义可得EF=(3x+4x)=10,即可求解x值,进而可求得AB的长.
【解答】解:设BD=x,
∵BD=AB=CD,
∴AB=3x,CD=4x,
∵线段AB,CD的中点E,F之间的距离是10cm,
∴EF=BE+BF=AB+CD=(AB+CD)=(3x+4x)=10cm,
解得x=,
∴AB=3x=(cm).
故答案为cm.
18.线段AB=5cm,点C在直线AB上,BC=3cm,则线段AC的一半是
1cm或4cm .
【分析】可分两种情况:当点C在线段AB上时,当C点在线段AB的延长线上时,分别求解AC的长,进而可求解.
【解答】解:当点C在线段AB上时,AC=AB﹣BC=5﹣3=2(cm),
∴线段AC的一半为1cm;
当C点在线段AB的延长线上时,AC=AB+BC=5+3=8(cm),
∴线段AC的一半为4cm,
即线段AC的一半为1cm或4cm,
故答案为1cm或4cm.
19九点45分时,钟面上的时针与分针的夹角是
度.
【考点】钟面角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】22.5.
【分析】9点45分时,分针指向9,时针在指向9与10之间,则时针45分钟转过的角度即为8时45分时,时钟的时针与分针的夹角度数,根据时针每分钟转0.5°,计算0.5°×45即可.
【解答】解:∵9点45分时,分针指向9,时针在指向9与10之间,
∴时针45分钟转过的角度即为9时45分时,时钟的时针与分针的夹角度数,即0.5°×45=22.5°.
故答案为:22.5.
20若a2+b2=5,ab=2,则(a+b)2= .
【考点】完全平方公式.
【专题】计算题.
【答案】见试题解答内容
【分析】根据完全平方公式直接代入解答即可.
【解答】解:∵(a+b)2=a2+b2+2ab,
∴把a2+b2与ab代入,得
(a+b)2=5+2×2=9.
21计算:
(1)(x﹣2y+1)(x+2y﹣1)﹣(x+2y+1)(x﹣2y﹣1);
(2)[(x﹣3y)(x+3y)+(3y﹣x)2]÷(﹣2x).
【考点】整式的混合运算.
【专题】计算题;整式;运算能力.
【答案】(1)8y;(2)﹣x+3y.
【分析】(1)先利用平方差公式计算乘法,然后再去括号,最后合并同类项;
(2)先利用平方差公式和完全平方公式计算乘方和乘法,然后再计算多项式除以单项式.
【解答】解:(1)原式=[x﹣(2y﹣1)][x+(2y﹣1)]﹣[x+(2y+1)][x﹣(2y+1)]
=[x2﹣(2y﹣1)2]﹣[x2﹣(2y+1)2]
=[x2﹣(4y2﹣4y+1)]﹣[x2﹣(4y2+4y+1)]
=(x2﹣4y2+4y﹣1)﹣(x2﹣4y2﹣4y﹣1)
=x2﹣4y2+4y﹣1﹣x2+4y2+4y+1
=8y;
(2)原式=(x2﹣9y2+9y2﹣6xy+x2)÷(﹣2x)
=(2x2﹣6xy)÷(﹣2x)
=﹣x+3y.
22先化简,再求值:(x﹣y2)﹣(x﹣y)(x+y)+(x+y)2,其中x2﹣2x+1+(y+3)2=0.
【考点】非负数的性质:偶次方;整式的混合运算—化简求值.
【专题】计算题;整式;运算能力.
【答案】x+2xy+y2,4.
【分析】先利用平方差公式和完全平方公式计算乘方和乘法,然后再算加减,最后根据完全平方式的非负性确定x,y的值,代入求值即可.
【解答】解:原式=x﹣y2﹣(x2﹣y2)+(x2+2xy+y2)
=x﹣y2﹣x2+y2+x2+2xy+y2
=x+2xy+y2,
∵x2﹣2x+1+(y+3)2=0,
∴(x﹣1)2+(y+3)2=0,
∴x﹣1=0,y+3=0,
∴x=1,y=﹣3,
原式=1+2×1×(﹣3)+(﹣3)2
=1﹣6+9
=4.
23一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
【考点】一次函数的应用.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)由图象可知,当x=0时,y=5,所以农民自带的零钱是5元.
(2)可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式.
(3)可设降价后农民手中钱y与所售土豆千克数x之间的函数关系式,因为当x=a时,y=26,当x=30时,y=20,依此列出方程求解.
【解答】解:(1)由图象可知,当x=0时,y=5.
答:农民自带的零钱是5元.
(2)设降价前每千克土豆价格为k元,
则农民手中钱y与所售土豆千克数x之间的函数关系式为:y=kx+5,
∵当x=30时,y=20,
∴20=30k+5,
解得k=0.5.
答:降价前每千克土豆价格为0.5元.
(3)设降价后农民手中钱y与所售土豆千克数x之间的函数关系式为y=0.4x+b.
∵当x=30时,y=20,
∴b=8,
当x=a时,y=26,即0.4a+8=26,
解得:a=45.
答:农民一共带了45千克土豆.
24已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.
【考点】平行线的判定与性质.
【专题】证明题.
【答案】见试题解答内容
【分析】由垂直于同一条直线的两直线平行得到CD与EF平行,利用两直线平行得到一对内错角相等,再由DE与BC平行,利用两直线平行得到另一对内错角相等,等量代换即可得证.
【解答】证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠FED=∠EDC,
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠FED=∠BCD.
25“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数分布直方图和扇形统计图.
(1)求本次比赛参赛选手总人数,并补全频数分布直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,求男生、女生各多少人?
【考点】频数(率)分布直方图;扇形统计图.
【专题】数据的收集与整理;统计的应用;数据分析观念;运算能力.
【答案】(1)36,补全统计图详见解答;
(2)50°;
(3)男生3人,女生2人.
【分析】(1)根据“C组”所对应的圆心角度数,可得出“C组”所占的百分比,再根据频率=求出调查人数,进而计算出“B组”频数,补全频数分布直方图;
(2)求出“D组”所占整体的百分比,即可求出相应的圆心角度数;
(3)根据“D组”的人数求解即可.
【解答】解:(1)“C组”所占的百分比为:×100%=25%,
本次参赛人数为:9÷25%=36(人),
“B组”人数为:36×50%=18(人),
“80≤x<85”的人数为:18﹣11=7(人),
“95≤x<100”的人数为:36﹣4﹣18﹣9=5(人),
答:本次比赛参赛选手总人数为44人,补全频数分布直方图如下:
(2)360°×=50°,
答:扇形统计图中扇形D的圆心角度数为50°;
(3)由频数分布直方图可知,
“D组”的有5人,男生比女生多1人,
所以男生3人,女生2人,
答:成绩在D区域的选手中,男生比女生多一人,男生有3人、女生有2人.
26如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
【考点】角平分线的定义;平行线的性质.
【答案】见试题解答内容
【分析】由CB平分∠ACD,∠ACD=140°,推出∠DCB=70°,由AB∥CD,证得∠CBA=∠DCB=70°,进而求得∠FAB,故得到∠EFB+∠FBA=180°,由平行线的判定证得EF∥AB,即可证得∠CEF=∠A,从而求出∠ACD=140°,即可证得结论.
【解答】解:∵CB平分∠ACD,∠ACD=140°,
∴∠DCB=70°,
∵AB∥CD,
∴∠CBA=∠DCB=70°,
∵∠CBF=20°,
∴∠FAB=70°﹣20°=50°,
∵∠EFB=130°,
∴∠EFB+∠FBA=180°,
∴EF∥AB,
∴∠CEF=∠A,
∵AB∥CD,∠ACD=140°,
∴∠A=180﹣140°=40°,
∴∠CEF=40°.
27如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个长方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
【考点】平方差公式的几何背景.
【答案】见试题解答内容
【分析】(1)根据两个图形的面积相等,即可写出公式;
(2)根据面积相等可得(a+b)(a﹣b)=a2﹣b2;
(3)从左到右依次利用平方差公式即可求解.
【解答】解:(1),S2=(a+b)(a﹣b);
(2)(a+b)(a﹣b)=a2﹣b2;
(3)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)+1
=(22﹣1)(22+1)(24+1)(28+1)+1
=(24﹣1)(24+1)(28+1)+1
=(28﹣1)(28+1)+1
=(216﹣1)+1
=216.
一、选择题(本大题共12个小题,每小题4分,共48分.每小题给出的四个答案中,只有一项是正确的.)
1.平面上有四点,经过其中的两点画直线最多可画出( )
A.三条
B.四条
C.五条
D.六条
2.下列运算正确的是( )
A.a2+a2=a4
B.a3?a4=a12
C.(a3)4=a12
D.(ab)2=ab2
3.生物学家发现了一种病毒,其长度约为0.00000032mm,它的1%用科学记数法表示正确的是( )
A.3.2×10﹣10
B.3.2×10﹣8
C.3.2×10﹣7
D.3.2×10﹣9
4.中学生骑电动车上学给交通安全带来隐患,为了解某中学2500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A.该校约有90%的家长持反对态度
B.调查方式是普查
C.该校只有360个家长持反对态度
D.样本是360个家长
5.下列说法中,正确的个数是( )
(1)过两点有且只有一条线段;
(2)连接两点的线段的长度叫做两点的距离:
(3)两点之间,线段最短;
(4)AB=BC,则点B是线段AC的中点;
(5)射线比直线短.
A.1
B.2
C.3
D.4
6.如图直线l1∥l2,AB⊥CD,∠1=34°,那么∠2的度数是( )
A.34°
B.56°
C.46°
D.44°
7.如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠A=180°,所以BC∥AD.
A.1个
B.2个
C.3个
D.4个
8.如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
A.5°
B.10°
C.15°
D.20°
9.已知∠A=40°,则∠A的余角的补角是( )
A.130°
B.120°
C.50°
D.60°
10.过多边形的一条边(不含顶点)上的一个点向各顶点连线,可将此多边形分成7个三角形,则此多边形的边数为( )
A.6
B.7
C.8
D.9
11.如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )
A.垂直
B.相交
C.平行
D.不能确定
12.正方形边长为5厘米,若边长减少x,则面积减少y.下列说法正确的是( )
A.边长x是自变量,面积减少量y是因变量
B.边长是自变量,面积是因变量
C.上述关系式为y=(5﹣x)2
D.上述关系式为y=52﹣(5﹣x)2
二、填空题(本大题共8小题,每小题4分,共32分.只要求填写最后结果)
13.若m2﹣2km+是关于m的完全平方式,则k的值是
.
14.一个人从A地出发沿北偏东60°方向走到B地,再从B地出发沿南偏西20°方向走到C地,那么∠ABC=
度.
15.如图所示,将长方形纸片ABCD进行折叠,如果∠BHG=70°,那么∠BHE=
度.
16.如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP与∠EFP的平分线相交于点P,且∠EFD=60°,EP⊥FP,则∠BEP=
度.
17.如图,已知AB和CD的公共部分BD=AB=CD,线段AB,CD的中点E,F之间的距离是10cm,则AB的长是
.
18.线段AB=5cm,点C在直线AB上,BC=3cm,则线段AC的一半是
.
19九点45分时,钟面上的时针与分针的夹角是
度.
20若a2+b2=5,ab=2,则(a+b)2= .
三、解答题(本大题共7小题,共70分写出必要的文字说明、证明过程或推演步骤)
21计算:
(1)(x﹣2y+1)(x+2y﹣1)﹣(x+2y+1)(x﹣2y﹣1);
(2)[(x﹣3y)(x+3y)+(3y﹣x)2]÷(﹣2x).
22先化简,再求值:(x﹣y2)﹣(x﹣y)(x+y)+(x+y)2,其中x2﹣2x+1+(y+3)2=0.
23一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
24已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.
25“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数分布直方图和扇形统计图.
(1)求本次比赛参赛选手总人数,并补全频数分布直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,求男生、女生各多少人?
26如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
27如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个长方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
参考答案与试题解析
一.选择题(共12小题)
1.平面上有四点,经过其中的两点画直线最多可画出( )
A.三条
B.四条
C.五条
D.六条
【分析】画出图形即可确定最多能画的直线的条数.
【解答】解:如图,最多可画6条直线.
,
故选:D.
2.下列运算正确的是( )
A.a2+a2=a4
B.a3?a4=a12
C.(a3)4=a12
D.(ab)2=ab2
【分析】分别根据合并同类项的法则、同底数幂的乘法、幂的乘方以及积的乘方化简即可判断.
【解答】解:A.a2+a2=2a2,故选项A不合题意;
B.a3?a4=a7,故选项B不合题意;
C.(a3)4=a12,故选项C符合题意;
D.(ab)2=a2b2,故选项D不合题意.
故选:C.
3.生物学家发现了一种病毒,其长度约为0.00000032mm,它的1%用科学记数法表示正确的是( )
A.3.2×10﹣10
B.3.2×10﹣8
C.3.2×10﹣7
D.3.2×10﹣9
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00000032×1%=0.0000000032=3.2×10﹣9.
故选:D.
4.中学生骑电动车上学给交通安全带来隐患,为了解某中学2500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A.该校约有90%的家长持反对态度
B.调查方式是普查
C.该校只有360个家长持反对态度
D.样本是360个家长
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:A.该校约有90%的家长持反对态度,说法正确,故本选项符合题意;
B.调查方式是抽样调查,故本选项不合题意;
C.该校有2250个家长持反对态度,故本选项不合题意;
D.样本是400个家长对“中学生骑电动车上学”的态度,故本选项不合题意;
故选:A.
5.下列说法中,正确的个数是( )
(1)过两点有且只有一条线段;
(2)连接两点的线段的长度叫做两点的距离:
(3)两点之间,线段最短;
(4)AB=BC,则点B是线段AC的中点;
(5)射线比直线短.
A.1
B.2
C.3
D.4
【分析】根据直线,线段的性质,两点间距离的定义,对各小题分析判断后利用排除法求解.
【解答】解:(1过两点有且只有一条线段,错误;
(2)应为连接两点的线段的长度叫做两点的距离,故本小题正确:
(3)两点之间,线段最短,正确;
(4)AB=BC,则点B是线段AC的中点,错误,因为A、B、C三点不一定在同一直线上,故本小题错误;
(5)射线比直线短,错误,射线与直线不能比较长短,故本小题错误.
综上所述,正确的有(2)(3)共2个.
故选:B.
6.如图直线l1∥l2,AB⊥CD,∠1=34°,那么∠2的度数是( )
A.34°
B.56°
C.46°
D.44°
【分析】根据垂直的定义得到∠4=90°,根据三角形外角性质有∠4=∠1+∠3,则∠3=90°﹣∠1=90°﹣34°=56°,由l1∥l2,根据两直线平行,同位角相等即可得到∠2=∠3=56°.
【解答】解:如图:
∵AB⊥CD,
∴∠4=90°,
∵∠4=∠1+∠3,∠1=34°,
∴∠3=90°﹣∠1=90°﹣34°=56°,
∵l1∥l2,
∴∠2=∠3=56°.
故选:B.
7.如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠A=180°,所以BC∥AD.
A.1个
B.2个
C.3个
D.4个
【分析】根据平行线的判定定理判断求解即可.
【解答】解:∵∠1=∠4,
∴AB∥CD,
故①错误,不符合题意;
∵∠2=∠3,
∴BC∥AD,
故②错误,不符合题意;
∵∠BCD+∠ADC=180°,
∴AD∥BC,
故③正确,符合题意;
∵∠1+∠2+∠A=180°,
即∠ABC+∠A=180°,
∴BC∥AD,
故④正确,符合题意;
故推理符合题意的有2个,
故选:B.
8.如图,OB平分∠AOD,OC平分∠BOD,∠AOC=45°,则∠BOC=( )
A.5°
B.10°
C.15°
D.20°
【分析】利用角平分线得到∠AOB=∠BOD=2∠BOC,借助图形即可求出∠BOC.
【解答】解:∵OC平分∠BOD,
∴∠BOD=2∠BOC,
∵OB平分∠AOD,
∴∠AOB=∠BOD=2∠BOC,
∵∠AOC=45°,
∴∠AOC=∠AOB+∠BOC=2∠BOC+∠BOC=3∠BOC=45°,
∴∠BOC=∠AOC=15°,
故选:C.
9.已知∠A=40°,则∠A的余角的补角是( )
A.130°
B.120°
C.50°
D.60°
【分析】先计算出∠A的余角,再计算出它余角的补角.
【解答】解:因为∠A=40°,
所以∠A的余角就是:90°﹣40°=50°.
而∠A的余角的补角就是:180°﹣50°=130°.
故选:A.
10.过多边形的一条边(不含顶点)上的一个点向各顶点连线,可将此多边形分成7个三角形,则此多边形的边数为( )
A.6
B.7
C.8
D.9
【分析】若P点取在一边上(不含顶点),则可以与其他顶点连接出(n﹣2)条线段,可以分n边形为(n﹣1)个三角形.
【解答】解:此多边形的边数为:7+1=8.
故选:C.
11.如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )
A.垂直
B.相交
C.平行
D.不能确定
【分析】由两条平行线被第三条直线所截,根据两直线平行,同位角相等,即可得一组同位角相等即∠FEB=∠GFD,又由角平分线的性质求得∠1=∠2,然后根据同位角相等,两直线平行,即可求得答案.
【解答】解:∵AB∥CD,
∴∠FEB=∠GFD,
∵EM与FN分别是∠FEM与∠GFD的平分线,
∴∠1=∠FEB,∠2=∠GFD,
∴∠1=∠2,
∴EM∥FN.
故选:C.
12.正方形边长为5厘米,若边长减少x,则面积减少y.下列说法正确的是( )
A.边长x是自变量,面积减少量y是因变量
B.边长是自变量,面积是因变量
C.上述关系式为y=(5﹣x)2
D.上述关系式为y=52﹣(5﹣x)2
【分析】根据题意可得减小后的边长及减小后的面积,进而可得面积的减小量y与x的关系式,由此可判断C,D选项;结合函数关系式根据自变量和因变量的概念可判断A,B选项.
【解答】解:由题意得边长减小为5﹣x,减小后的面积为(5﹣x)2,
∴y与x的关系式为y=52﹣(5﹣x)2;
由因变量和自变量的概念可知:x是自变量,y是因变量,即边长减小量为自变量,面积减少量是因变量,
故选:D.
二.填空题(共6小题)
13.若m2﹣2km+是关于m的完全平方式,则k的值是
﹣或 .
【分析】根据完全平方式得出﹣2k=±2×,再求出即可.
【解答】解:∵m2﹣2km+是关于m的完全平方式,
∴﹣2k=±2×,
解得:k=﹣或,
故答案为:﹣或.
14.一个人从A地出发沿北偏东60°方向走到B地,再从B地出发沿南偏西20°方向走到C地,那么∠ABC= 40 度.
【分析】根据方位角的概念,画图正确表示出行驶的过程,再根据已知转向的角度结合三角形的内角和与外角的关系求解.
【解答】解:如图,A沿北偏东60°的方向行驶到B,则∠BAC=90°﹣60°=30°,
B沿南偏西20°的方向行驶到C,则∠BCO=90°﹣20°=70°,
又∵∠ABC=∠BCO﹣∠BAC,
∴∠ABC=70°﹣30°=40°.
故答案为:40.
15.如图所示,将长方形纸片ABCD进行折叠,如果∠BHG=70°,那么∠BHE= 55 度.
【分析】利用平行线的性质可得∠1=70°,利用折叠及平行线的性质,三角形的内角和定理可得所求角的度数.
【解答】解:由题意得EF∥GH,
∴∠1=∠BHG=70°,
∴∠FEH+∠BHE=110°,
由折叠可得∠2=∠FEH,
∵AD∥BC
∴∠2=∠BHE,
∴∠FEH=∠BHE=55°.
故答案为55.
16.如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP与∠EFP的平分线相交于点P,且∠EFD=60°,EP⊥FP,则∠BEP= 60 度.
【分析】根据平行线的性质和角平分线的定义求解.
【解答】解:∵AB∥CD,
∴∠BEF=180﹣∠EFD=120°;
∵FP平分∠EFD,且∠EFD=60°,
∴∠EFP=30°,
在△EFP中,EP⊥FP,
∴∠FEP=60°;
∴∠BEP=∠BEF﹣∠FEP=60°,
故答案为:60.
17.如图,已知AB和CD的公共部分BD=AB=CD,线段AB,CD的中点E,F之间的距离是10cm,则AB的长是
cm .
【分析】设BD=x,则AB=3x,CD=4x,由中点的定义可得EF=(3x+4x)=10,即可求解x值,进而可求得AB的长.
【解答】解:设BD=x,
∵BD=AB=CD,
∴AB=3x,CD=4x,
∵线段AB,CD的中点E,F之间的距离是10cm,
∴EF=BE+BF=AB+CD=(AB+CD)=(3x+4x)=10cm,
解得x=,
∴AB=3x=(cm).
故答案为cm.
18.线段AB=5cm,点C在直线AB上,BC=3cm,则线段AC的一半是
1cm或4cm .
【分析】可分两种情况:当点C在线段AB上时,当C点在线段AB的延长线上时,分别求解AC的长,进而可求解.
【解答】解:当点C在线段AB上时,AC=AB﹣BC=5﹣3=2(cm),
∴线段AC的一半为1cm;
当C点在线段AB的延长线上时,AC=AB+BC=5+3=8(cm),
∴线段AC的一半为4cm,
即线段AC的一半为1cm或4cm,
故答案为1cm或4cm.
19九点45分时,钟面上的时针与分针的夹角是
度.
【考点】钟面角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】22.5.
【分析】9点45分时,分针指向9,时针在指向9与10之间,则时针45分钟转过的角度即为8时45分时,时钟的时针与分针的夹角度数,根据时针每分钟转0.5°,计算0.5°×45即可.
【解答】解:∵9点45分时,分针指向9,时针在指向9与10之间,
∴时针45分钟转过的角度即为9时45分时,时钟的时针与分针的夹角度数,即0.5°×45=22.5°.
故答案为:22.5.
20若a2+b2=5,ab=2,则(a+b)2= .
【考点】完全平方公式.
【专题】计算题.
【答案】见试题解答内容
【分析】根据完全平方公式直接代入解答即可.
【解答】解:∵(a+b)2=a2+b2+2ab,
∴把a2+b2与ab代入,得
(a+b)2=5+2×2=9.
21计算:
(1)(x﹣2y+1)(x+2y﹣1)﹣(x+2y+1)(x﹣2y﹣1);
(2)[(x﹣3y)(x+3y)+(3y﹣x)2]÷(﹣2x).
【考点】整式的混合运算.
【专题】计算题;整式;运算能力.
【答案】(1)8y;(2)﹣x+3y.
【分析】(1)先利用平方差公式计算乘法,然后再去括号,最后合并同类项;
(2)先利用平方差公式和完全平方公式计算乘方和乘法,然后再计算多项式除以单项式.
【解答】解:(1)原式=[x﹣(2y﹣1)][x+(2y﹣1)]﹣[x+(2y+1)][x﹣(2y+1)]
=[x2﹣(2y﹣1)2]﹣[x2﹣(2y+1)2]
=[x2﹣(4y2﹣4y+1)]﹣[x2﹣(4y2+4y+1)]
=(x2﹣4y2+4y﹣1)﹣(x2﹣4y2﹣4y﹣1)
=x2﹣4y2+4y﹣1﹣x2+4y2+4y+1
=8y;
(2)原式=(x2﹣9y2+9y2﹣6xy+x2)÷(﹣2x)
=(2x2﹣6xy)÷(﹣2x)
=﹣x+3y.
22先化简,再求值:(x﹣y2)﹣(x﹣y)(x+y)+(x+y)2,其中x2﹣2x+1+(y+3)2=0.
【考点】非负数的性质:偶次方;整式的混合运算—化简求值.
【专题】计算题;整式;运算能力.
【答案】x+2xy+y2,4.
【分析】先利用平方差公式和完全平方公式计算乘方和乘法,然后再算加减,最后根据完全平方式的非负性确定x,y的值,代入求值即可.
【解答】解:原式=x﹣y2﹣(x2﹣y2)+(x2+2xy+y2)
=x﹣y2﹣x2+y2+x2+2xy+y2
=x+2xy+y2,
∵x2﹣2x+1+(y+3)2=0,
∴(x﹣1)2+(y+3)2=0,
∴x﹣1=0,y+3=0,
∴x=1,y=﹣3,
原式=1+2×1×(﹣3)+(﹣3)2
=1﹣6+9
=4.
23一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
【考点】一次函数的应用.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)由图象可知,当x=0时,y=5,所以农民自带的零钱是5元.
(2)可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式.
(3)可设降价后农民手中钱y与所售土豆千克数x之间的函数关系式,因为当x=a时,y=26,当x=30时,y=20,依此列出方程求解.
【解答】解:(1)由图象可知,当x=0时,y=5.
答:农民自带的零钱是5元.
(2)设降价前每千克土豆价格为k元,
则农民手中钱y与所售土豆千克数x之间的函数关系式为:y=kx+5,
∵当x=30时,y=20,
∴20=30k+5,
解得k=0.5.
答:降价前每千克土豆价格为0.5元.
(3)设降价后农民手中钱y与所售土豆千克数x之间的函数关系式为y=0.4x+b.
∵当x=30时,y=20,
∴b=8,
当x=a时,y=26,即0.4a+8=26,
解得:a=45.
答:农民一共带了45千克土豆.
24已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.
【考点】平行线的判定与性质.
【专题】证明题.
【答案】见试题解答内容
【分析】由垂直于同一条直线的两直线平行得到CD与EF平行,利用两直线平行得到一对内错角相等,再由DE与BC平行,利用两直线平行得到另一对内错角相等,等量代换即可得证.
【解答】证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠FED=∠EDC,
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠FED=∠BCD.
25“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数分布直方图和扇形统计图.
(1)求本次比赛参赛选手总人数,并补全频数分布直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,求男生、女生各多少人?
【考点】频数(率)分布直方图;扇形统计图.
【专题】数据的收集与整理;统计的应用;数据分析观念;运算能力.
【答案】(1)36,补全统计图详见解答;
(2)50°;
(3)男生3人,女生2人.
【分析】(1)根据“C组”所对应的圆心角度数,可得出“C组”所占的百分比,再根据频率=求出调查人数,进而计算出“B组”频数,补全频数分布直方图;
(2)求出“D组”所占整体的百分比,即可求出相应的圆心角度数;
(3)根据“D组”的人数求解即可.
【解答】解:(1)“C组”所占的百分比为:×100%=25%,
本次参赛人数为:9÷25%=36(人),
“B组”人数为:36×50%=18(人),
“80≤x<85”的人数为:18﹣11=7(人),
“95≤x<100”的人数为:36﹣4﹣18﹣9=5(人),
答:本次比赛参赛选手总人数为44人,补全频数分布直方图如下:
(2)360°×=50°,
答:扇形统计图中扇形D的圆心角度数为50°;
(3)由频数分布直方图可知,
“D组”的有5人,男生比女生多1人,
所以男生3人,女生2人,
答:成绩在D区域的选手中,男生比女生多一人,男生有3人、女生有2人.
26如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
【考点】角平分线的定义;平行线的性质.
【答案】见试题解答内容
【分析】由CB平分∠ACD,∠ACD=140°,推出∠DCB=70°,由AB∥CD,证得∠CBA=∠DCB=70°,进而求得∠FAB,故得到∠EFB+∠FBA=180°,由平行线的判定证得EF∥AB,即可证得∠CEF=∠A,从而求出∠ACD=140°,即可证得结论.
【解答】解:∵CB平分∠ACD,∠ACD=140°,
∴∠DCB=70°,
∵AB∥CD,
∴∠CBA=∠DCB=70°,
∵∠CBF=20°,
∴∠FAB=70°﹣20°=50°,
∵∠EFB=130°,
∴∠EFB+∠FBA=180°,
∴EF∥AB,
∴∠CEF=∠A,
∵AB∥CD,∠ACD=140°,
∴∠A=180﹣140°=40°,
∴∠CEF=40°.
27如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个长方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
【考点】平方差公式的几何背景.
【答案】见试题解答内容
【分析】(1)根据两个图形的面积相等,即可写出公式;
(2)根据面积相等可得(a+b)(a﹣b)=a2﹣b2;
(3)从左到右依次利用平方差公式即可求解.
【解答】解:(1),S2=(a+b)(a﹣b);
(2)(a+b)(a﹣b)=a2﹣b2;
(3)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)+1
=(22﹣1)(22+1)(24+1)(28+1)+1
=(24﹣1)(24+1)(28+1)+1
=(28﹣1)(28+1)+1
=(216﹣1)+1
=216.
同课章节目录
