湘教版七年级上册数学 4.1.2从不同方向看立体图形和立体图形的展开 课件(共22张PPT)
文档属性
| 名称 | 湘教版七年级上册数学 4.1.2从不同方向看立体图形和立体图形的展开 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 13:20:47 | ||
图片预览






文档简介
(共22张PPT)
第1节
几何图形
第4章
图形的认识
第2课时
从不同方向看立体图形和立体图形的展开
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
从不同方向看立体图形
立体图形的展开
课时导入
复习提问
引出问题
如图所示的美丽景色,就像诗人苏轼的名诗“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”原诗意:从正面看庐山山岭连绵起伏,从侧面看庐山山峰耸立,从远处、近处、高处、低处看庐山,庐山呈现各种不同的样子.人不清楚庐山本来的面目,只因为自己在庐山中.这首诗蕴含什么样的数学思想呢?读这首诗的时候,你会想到吗?
在现实生活中,同一个物体,从不同方向看到不同
形状,你能找出一个从不同方向看,看到的形状都
相同的物体吗?
知识点
从不同方向看立体图形
知1-导
感悟新知
1
从三个不同的方向看一个物体,一般是从正面、上面和侧面,然后描绘三张所看到的图,即视图.这样就把一个物体转化为平面的图形.
知1-讲
感悟新知
1.对于一些立体图形,从不同的方向去看,往往会得到不同形状的平面图形,一般从三个方向看:从正面看、从左面看、从上面看.
2.画从不同方向看立体图形得到的平面图形时,看得见的轮廓线画成实线,看不见的轮麻线画成虚线.
知识链接
一些立体图形的问题,常把它们转化成平面图形来研究,从不同方向看立体图形得到不同形状的平面图形,就是其中一种研究方式,在建筑和工程设计中应用较多.
知1-讲
感悟新知
3.常见的立体图形从不同方向看到的平面图形:
知1-讲
感悟新知
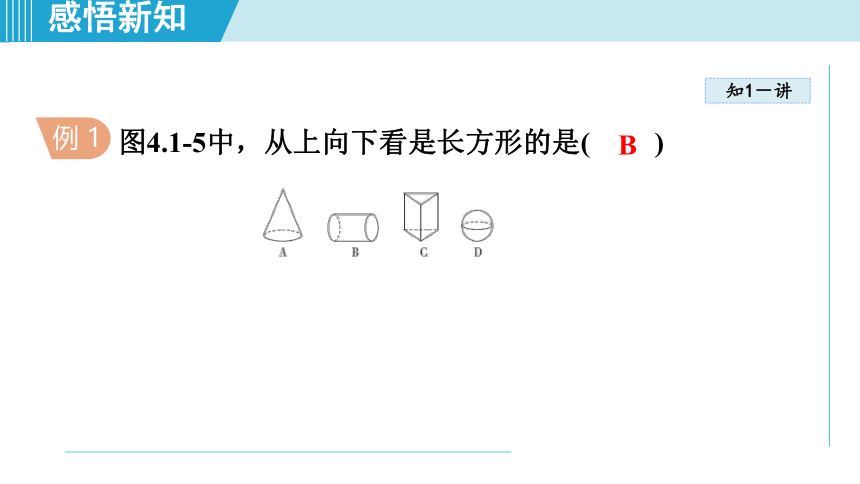
例
1
图4.1-5中,从上向下看是长方形的是(
)
B
知1-讲
感悟新知
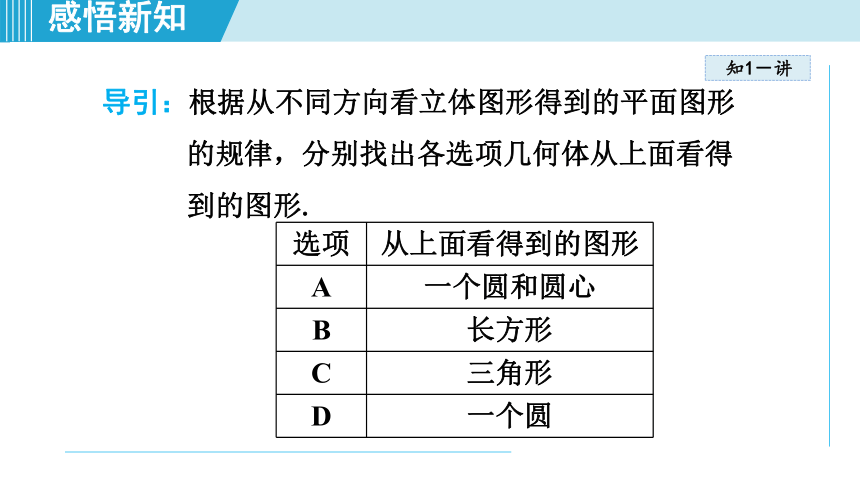
导引:根据从不同方向看立体图形得到的平面图形的规律,分别找出各选项几何体从上面看得到的图形.
选项
从上面看得到的图形
A
一个圆和圆心
B
长方形
C
三角形
D
一个圆
知1-讲
总
结
感悟新知
从不同的方向看物体,一定找准方向,发挥自己的想象力,找出看到的平面图形注意常见几何体从不同方向看到的平面图形.
1.下列立体图形中,左视图是圆的是( )
2.如图所示的正六棱柱的主视图是( )
知1-练
感悟新知
D
B
知2-导
感悟新知
知识点
立体图形的展开
2
虽然立体图形与平面图形是两类不同的几何图形,但他们是相互联系的,立体图形中某些部分是平面图形,如正方体的每个侧面都是正方形.
知2-导
感悟新知
从不同方向看立体图形,往往会得到不同形状的平面图形。如图4-4,整体上看,我们看到的是长方体;看不同侧面,看到的是长方形或正方形;从长方形或正方形中,我们还可以看到点、线段.
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形(如图4-5所示)
知2-讲
感悟新知
1.立体图形的展开图:有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开开图;同时这个平面图形可以折叠成相应的立体图形.
特别解读
同一个立体图形,按不同的方式展开,可能得到不同的平面图形.不是所有的立体图形都有展开图,如球就没有展开图.
知2-讲
感悟新知
2.展开和折叠是互递过程.
3.判断一个平面图形能否折叠成立体图形的方法:一看面数够不够;二看各面的位置是否合适,尤其是底面的位置;三看对应边的长度是否相等.
知2-讲
感悟新知
例2
图4.1-9中能折叠成正方体的是(
)
D
知2-讲
感悟新知
导引:常见的正方体的展开图如图4.1-10.解答这类题可以根据几何体的展开图特点,充分发挥空间想象能力直接判断,或通过动手折叠或展开确定正确结果.
知2-讲
感悟新知
总
结
用口诀“一线不过四,凹、田应弃之”,即一条线超过4个正方形,有凹字(如B,C),田字(如A)都不能折叠成正方体,可以判断是否为正方体的展开图;同时,充分发挥想象力和动手实践是解决此类问题的有效途径.
1.下列图形中,不可以作为一个正方体的展开图的是( )
知2-练
感悟新知
C
2.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
知2-练
感悟新知
B
课堂小结
从不同方向看立体图形和立体图形的展开
1.从不同的方向看立体图形的技巧:
(1)从正面看立体图形时,可以想象为:将立体图形从前向后压缩,使看到的面全部落在同一竖直的平面内.
(2)从左面看立体图形时,可以想象为:将立体图形从左向右压缩,使看到的面全部落在同一竖直的平面内.
(3)从上面看立体图形时,可以想象为:将立体图形从上向下压缩,使看到的面全部落在同一水平的平面内.
课堂小结
2.
重要知识点
知识点解析
特别注意的问题
立体图形的展开图
立体图形的展开图是平面图形.
正方体的展开图有多种情况,圆柱与圆锥的展开图不要忽略底面.
解题方法小结
结合实例,体会立体图形的表面展开图的展开过程,不断提高对几何体的展开图形认识
从不同方向看立体图形和立体图形的展开
必做:
请完成教材课后习题
课后作业
作业
第1节
几何图形
第4章
图形的认识
第2课时
从不同方向看立体图形和立体图形的展开
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
从不同方向看立体图形
立体图形的展开
课时导入
复习提问
引出问题
如图所示的美丽景色,就像诗人苏轼的名诗“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”原诗意:从正面看庐山山岭连绵起伏,从侧面看庐山山峰耸立,从远处、近处、高处、低处看庐山,庐山呈现各种不同的样子.人不清楚庐山本来的面目,只因为自己在庐山中.这首诗蕴含什么样的数学思想呢?读这首诗的时候,你会想到吗?
在现实生活中,同一个物体,从不同方向看到不同
形状,你能找出一个从不同方向看,看到的形状都
相同的物体吗?
知识点
从不同方向看立体图形
知1-导
感悟新知
1
从三个不同的方向看一个物体,一般是从正面、上面和侧面,然后描绘三张所看到的图,即视图.这样就把一个物体转化为平面的图形.
知1-讲
感悟新知
1.对于一些立体图形,从不同的方向去看,往往会得到不同形状的平面图形,一般从三个方向看:从正面看、从左面看、从上面看.
2.画从不同方向看立体图形得到的平面图形时,看得见的轮廓线画成实线,看不见的轮麻线画成虚线.
知识链接
一些立体图形的问题,常把它们转化成平面图形来研究,从不同方向看立体图形得到不同形状的平面图形,就是其中一种研究方式,在建筑和工程设计中应用较多.
知1-讲
感悟新知
3.常见的立体图形从不同方向看到的平面图形:
知1-讲
感悟新知
例
1
图4.1-5中,从上向下看是长方形的是(
)
B
知1-讲
感悟新知
导引:根据从不同方向看立体图形得到的平面图形的规律,分别找出各选项几何体从上面看得到的图形.
选项
从上面看得到的图形
A
一个圆和圆心
B
长方形
C
三角形
D
一个圆
知1-讲
总
结
感悟新知
从不同的方向看物体,一定找准方向,发挥自己的想象力,找出看到的平面图形注意常见几何体从不同方向看到的平面图形.
1.下列立体图形中,左视图是圆的是( )
2.如图所示的正六棱柱的主视图是( )
知1-练
感悟新知
D
B
知2-导
感悟新知
知识点
立体图形的展开
2
虽然立体图形与平面图形是两类不同的几何图形,但他们是相互联系的,立体图形中某些部分是平面图形,如正方体的每个侧面都是正方形.
知2-导
感悟新知
从不同方向看立体图形,往往会得到不同形状的平面图形。如图4-4,整体上看,我们看到的是长方体;看不同侧面,看到的是长方形或正方形;从长方形或正方形中,我们还可以看到点、线段.
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形(如图4-5所示)
知2-讲
感悟新知
1.立体图形的展开图:有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开开图;同时这个平面图形可以折叠成相应的立体图形.
特别解读
同一个立体图形,按不同的方式展开,可能得到不同的平面图形.不是所有的立体图形都有展开图,如球就没有展开图.
知2-讲
感悟新知
2.展开和折叠是互递过程.
3.判断一个平面图形能否折叠成立体图形的方法:一看面数够不够;二看各面的位置是否合适,尤其是底面的位置;三看对应边的长度是否相等.
知2-讲
感悟新知
例2
图4.1-9中能折叠成正方体的是(
)
D
知2-讲
感悟新知
导引:常见的正方体的展开图如图4.1-10.解答这类题可以根据几何体的展开图特点,充分发挥空间想象能力直接判断,或通过动手折叠或展开确定正确结果.
知2-讲
感悟新知
总
结
用口诀“一线不过四,凹、田应弃之”,即一条线超过4个正方形,有凹字(如B,C),田字(如A)都不能折叠成正方体,可以判断是否为正方体的展开图;同时,充分发挥想象力和动手实践是解决此类问题的有效途径.
1.下列图形中,不可以作为一个正方体的展开图的是( )
知2-练
感悟新知
C
2.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
知2-练
感悟新知
B
课堂小结
从不同方向看立体图形和立体图形的展开
1.从不同的方向看立体图形的技巧:
(1)从正面看立体图形时,可以想象为:将立体图形从前向后压缩,使看到的面全部落在同一竖直的平面内.
(2)从左面看立体图形时,可以想象为:将立体图形从左向右压缩,使看到的面全部落在同一竖直的平面内.
(3)从上面看立体图形时,可以想象为:将立体图形从上向下压缩,使看到的面全部落在同一水平的平面内.
课堂小结
2.
重要知识点
知识点解析
特别注意的问题
立体图形的展开图
立体图形的展开图是平面图形.
正方体的展开图有多种情况,圆柱与圆锥的展开图不要忽略底面.
解题方法小结
结合实例,体会立体图形的表面展开图的展开过程,不断提高对几何体的展开图形认识
从不同方向看立体图形和立体图形的展开
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
