湘教版七年级上册数学 4.3.3余角和补角 课件(共17张PPT)
文档属性
| 名称 | 湘教版七年级上册数学 4.3.3余角和补角 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第3节
角
第4章
图形的认识
第3课时
余角和补角
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
余角和补角
余角和补角的计算
课时导入
复习提问
引出问题
如果两个角的和是平角、直角时,这两个角的关系是怎样的呢?
知识点
余角和补角
知1-导
感悟新知
1
如图4-27,量一量,算一算,∠1+∠2,∠3+∠4的度数分别是多少?
知1-导
结
论
感悟新知
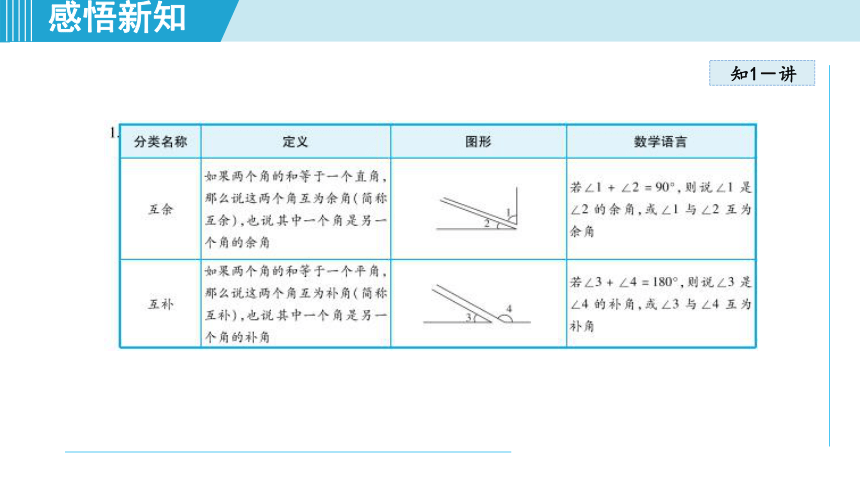
如果两个角的和等于一个直角,那么说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
如果两个角的和等于一个平角,那么说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
例如,34°的角与56°的角互为余角,图4-27(a)中∠1与∠2互为余角;48°的角与132°的角互为补角,图4-27(b)中∠3与∠4互为补角.
知1-讲
感悟新知
知1-讲
感悟新知
例
1
下列说法正确的有(
)
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3
B.4个
C.5个
D.6个
B
知1-讲
感悟新知
分析:主要紧扣锐角、直角、钝角、余角、补角的特征进行判断,除①②不正确外,其他说法都正确.
知1-讲
总
结
感悟新知
由于互余的两个角之和为90°,所以这两个角都为锐角;由于互补的两个角之和为180°,所以这两个角为一个锐角一个钟角或两个角都为直角.
1.中若一个角为65°,则它的补角的度数为( )
A.25°
B.35°
C.115°
D.125°
2.与30°的角互为余角的角的度数是( )
A.30°
B.60°
C.70°
D.90°
知1-练
感悟新知
C
B
知1-练
感悟新知
解:(1)错误;(2)错误.
2.判断下列说法的正误:
(1)已知∠1+∠2+∠3=90°,则∠1,∠2,∠3互为余角;
(2)互为余角或互为补角的两个角一定有公共边.
分析:互为余角或互为补角是针对两个角而言的,而且是两个角的度数关系,与角的位置没有关系.
知2-讲
感悟新知
知识点
余角和补角的计算
2
要点精析
(1)互余、互补必须是两个角之间的关系.
(2)互补的角不一定互为邻补角,但互为邻补角的角一定互为补角.
(3)互余或互补的角只与数量有关,与位置无关.
知2-讲
感悟新知
例2
如图4-29,∠AOB与∠BOD互为余角,OC是∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
解:因为∠AOB与∠BOD互为余角,所以∠BOD=
90°-∠AOB=90°-29.66°=60.34°.
又因为OC是∠BOD的平分线,所以∠COD=
∠BOD=
×60.34°
=30.17°.因此,∠COD的度数为30.17°,
知2-讲
感悟新知
总
结
两个角互余或互补只与它们的度数有关,而与它们的位置无关.
1.一个角比它的余角大10°,这个角为( )
A.40°
B.45°
C.50°
D.55°
2.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
A.互补
B.互余
C.相等
D.无法确定
知2-练
感悟新知
C
C
课堂小结
余角和补角
重要知识点
知识点解析
特别注意的问题
补角
?
如果两个角的度数之和等于180°(平角),就说这两个角互为补角,简称互补.
补角是两个角之间的关系,一个角不能说互补,三个以上角也不能说互补.
余角
?
两个角的度数之和等于90°(直角),就说这两个角互为余角,简称互余.
余角是两个角之间的关系,一个角不能说互余,三个以上角也不能说互余.
必做:
请完成教材课后习题
课后作业
作业
第3节
角
第4章
图形的认识
第3课时
余角和补角
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
余角和补角
余角和补角的计算
课时导入
复习提问
引出问题
如果两个角的和是平角、直角时,这两个角的关系是怎样的呢?
知识点
余角和补角
知1-导
感悟新知
1
如图4-27,量一量,算一算,∠1+∠2,∠3+∠4的度数分别是多少?
知1-导
结
论
感悟新知
如果两个角的和等于一个直角,那么说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
如果两个角的和等于一个平角,那么说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
例如,34°的角与56°的角互为余角,图4-27(a)中∠1与∠2互为余角;48°的角与132°的角互为补角,图4-27(b)中∠3与∠4互为补角.
知1-讲
感悟新知
知1-讲
感悟新知
例
1
下列说法正确的有(
)
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3
B.4个
C.5个
D.6个
B
知1-讲
感悟新知
分析:主要紧扣锐角、直角、钝角、余角、补角的特征进行判断,除①②不正确外,其他说法都正确.
知1-讲
总
结
感悟新知
由于互余的两个角之和为90°,所以这两个角都为锐角;由于互补的两个角之和为180°,所以这两个角为一个锐角一个钟角或两个角都为直角.
1.中若一个角为65°,则它的补角的度数为( )
A.25°
B.35°
C.115°
D.125°
2.与30°的角互为余角的角的度数是( )
A.30°
B.60°
C.70°
D.90°
知1-练
感悟新知
C
B
知1-练
感悟新知
解:(1)错误;(2)错误.
2.判断下列说法的正误:
(1)已知∠1+∠2+∠3=90°,则∠1,∠2,∠3互为余角;
(2)互为余角或互为补角的两个角一定有公共边.
分析:互为余角或互为补角是针对两个角而言的,而且是两个角的度数关系,与角的位置没有关系.
知2-讲
感悟新知
知识点
余角和补角的计算
2
要点精析
(1)互余、互补必须是两个角之间的关系.
(2)互补的角不一定互为邻补角,但互为邻补角的角一定互为补角.
(3)互余或互补的角只与数量有关,与位置无关.
知2-讲
感悟新知
例2
如图4-29,∠AOB与∠BOD互为余角,OC是∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
解:因为∠AOB与∠BOD互为余角,所以∠BOD=
90°-∠AOB=90°-29.66°=60.34°.
又因为OC是∠BOD的平分线,所以∠COD=
∠BOD=
×60.34°
=30.17°.因此,∠COD的度数为30.17°,
知2-讲
感悟新知
总
结
两个角互余或互补只与它们的度数有关,而与它们的位置无关.
1.一个角比它的余角大10°,这个角为( )
A.40°
B.45°
C.50°
D.55°
2.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
A.互补
B.互余
C.相等
D.无法确定
知2-练
感悟新知
C
C
课堂小结
余角和补角
重要知识点
知识点解析
特别注意的问题
补角
?
如果两个角的度数之和等于180°(平角),就说这两个角互为补角,简称互补.
补角是两个角之间的关系,一个角不能说互补,三个以上角也不能说互补.
余角
?
两个角的度数之和等于90°(直角),就说这两个角互为余角,简称互余.
余角是两个角之间的关系,一个角不能说互余,三个以上角也不能说互余.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
