2020-2021学年河北省沧州市沧县等五县联考七年级下学期期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年河北省沧州市沧县等五县联考七年级下学期期末数学试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 21:41:36 | ||
图片预览




文档简介
2020-2021学年河北省沧州市沧县等五县联考七年级(下)期末数学试卷
一、单选题(本大题共16个小题,1-10小题,每小题3分;11-16小题,每小题3分;共42分,在每小题给出的四个选项中,只有一项符合题目要求)
1.已知x,y满足方程组,则无论m取何值,x,y恒有关系式是( )
A.x+y=1
B.x+y=﹣1
C.x+y=9
D.x+y=﹣9
2.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
3.不等式组的解集在数轴上表示如图所示,则该不等式组可能为( )
A.
B.
C.
D.
4.下列各组图形中,AD是△ABC的高的图形是( )
A.
B.
C.
D.
5.冠状病毒因在显微镜下观察类似王冠而得名,新型冠状病毒是以前从未在人体中发现的冠状病毒,新型冠状病毒的半径约是0.000000045米,将数0.000000045用科学记数法表示为( )
A.4.5×108
B.45×10﹣7
C.4.5×10﹣8
D.0.45×10﹣9
6.下列各式由左边到右边的变形中,是分解因式的为( )
A.10x2﹣5x=5x?2x﹣5x
B.a(x+y)=ax+ay
C.x2﹣4x+4=(x﹣2)2
D.x2﹣16+3x=(x﹣4)(x+4)+3x
7.下列说法中,正确的是( )
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线垂直
D.同旁内角互补
8.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
9.若关于x的不等式组无解,则m的取值范围是( )
A.m>4
B.m<4
C.m≥4
D.m≤4
10.如果将一副三角板按如图方式叠放,那么∠1的度数是( )
A.90°
B.100°
C.105°
D.135°
11.(2分)若方程组的解中x+y=16,则k等于( )
A.15
B.18
C.16
D.17
12.(2分)已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0
B.1
C.2
D.3
13.(2分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
14.(2分)如图,把图1中的①部分剪下来,恰好能拼在②的位置处,构成图2中的图形,形成一个从边长为a的大正方形中剪掉一个边长为b的小正方形.根据图形的变化过程写出的一个正确的等式是( )
A.(a﹣b)=a2﹣2ab+b2
B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣b2
D.(a+b)(a﹣b)=a2﹣b2
15.(2分)将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
16.(2分)如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移5个单位长度就得到了另一直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )
①AC∥DF;
②HE=5;
③CF=5;
④四边形DHCF的面积为32.5.
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共4个小题,每小题3分,共12分)
17.若实数a、b满足:a+b=6,a﹣b=10,则2a2﹣2b2=
.
18.如图,在三角形ABC中,AC=5,BC=6,BC边上的高AD=4,若点P在边AC上(不与点A,C重合)移动,则线段BP最短时的长为
.
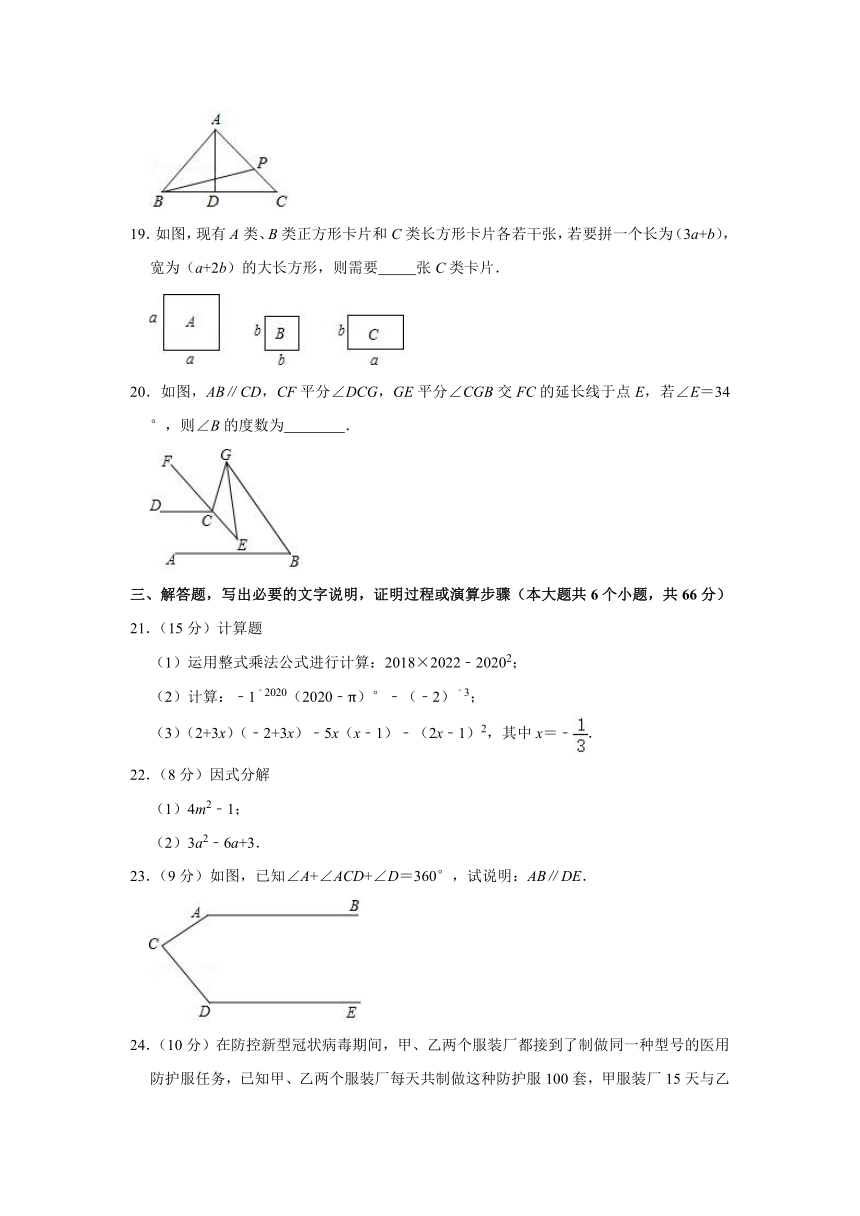
19.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要
张C类卡片.
20.如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为
.
三、解答题,写出必要的文字说明,证明过程或演算步骤(本大题共6个小题,共66分)
21.(15分)计算题
(1)运用整式乘法公式进行计算:2018×2022﹣20202;
(2)计算:﹣1﹣2020(2020﹣π)°﹣(﹣2)﹣3;
(3)(2+3x)(﹣2+3x)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
22.(8分)因式分解
(1)4m2﹣1;
(2)3a2﹣6a+3.
23.(9分)如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
24.(10分)在防控新型冠状病毒期间,甲、乙两个服装厂都接到了制做同一种型号的医用防护服任务,已知甲、乙两个服装厂每天共制做这种防护服100套,甲服装厂15天与乙服装厂10天制做的防护服套数相同.
(1)求甲、乙两个服装厂每天各制做多少套这种防护服.
(2)现有3000套这种防护服的制做任务,要求不超过25天完成,若乙服装厂每天多做8套,那么甲服装厂每天至少多做多少套?
25.(12分)阅读材料:
如果x是一个有理数,我们把不超过x的最大整数记作【x】.
例如,【3.2】=3,【5】=5,【﹣2.1】=﹣3.
那么,x=【x】+a,其中0≤a<1.
例如,3.2=【3.2】+0.2,5=【5】+0,﹣2.1=【﹣2.1】+0.9.
请你解决下列问题:
(1)【4.8】=
,【﹣6.5】=
;
(2)如果x=【3】,那么x的取值范围是
;
(3)如果【5x﹣2】=3x+1,那么x的值是
.
26.(12分)探索三角形的内角与外角平分线:
(1)已知,如图1,在△ABC中,两内角平分线,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=
;此时∠A与∠BOC有怎样的关系,试说明理由.
(2)已知,如图2,在△ABC中,一内角平分线BO平分∠ABC,一外角平分线CO平分∠ACE,若∠A=50°,则∠BOC=
;此时∠A与∠BOC有怎样的关系,试说明理由.
(3)已知,如图3,在△ABC中,∠ABC、∠ACB的外角平分线OB、OC相交于点O,若∠A=50°,则∠BOC=
;此时∠A与∠BOC有怎样的关系(不需说明理由)
图1中:关系式:
,理由:
;
图2中:关系式:
,理由:
;
图3中:关系式:
,理由:
.
2020-2021学年河北省沧州市沧县等五县联考七年级(下)期末数学试卷
参考答案与试题解析
一、单选题(本大题共16个小题,1-10小题,每小题3分;11-16小题,每小题3分;共42分,在每小题给出的四个选项中,只有一项符合题目要求)
1.已知x,y满足方程组,则无论m取何值,x,y恒有关系式是( )
A.x+y=1
B.x+y=﹣1
C.x+y=9
D.x+y=﹣9
【分析】由方程组消去m,得到一个关于x,y的方程,化简这个方程即可.
【解答】解:由方程组,
有y﹣5=m
∴将上式代入x+m=4,
得到x+(y﹣5)=4,
∴x+y=9.
故选:C.
2.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
【分析】根据不等式的性质解答.
【解答】解:A、若m=3,n=﹣2,则2m>3n,故不符合题意.
B、若m>n,则2+m>2+n,故符合题意.
C、若m>n,则2﹣m<2﹣n,故不符合题意.
D、若m>n,则>,故不符合题意.
故选:B.
3.不等式组的解集在数轴上表示如图所示,则该不等式组可能为( )
A.
B.
C.
D.
【分析】先根据在数轴上表示不等式解集的方法得出该不等式组的解集,再找出符合条件的不等式组即可.
【解答】解:由数轴上表示不等式解集的方法可知,该不等式组的解集为:﹣1<x≤2,
A.的解集是:﹣<x≤2,故本选项不合题意;
B.的解集是:﹣1<x≤2,故本选项符合题意;
C.无解,故本选项不合题意;
D.的解集是:x>2,故本选项不合题意;
故选:B.
4.下列各组图形中,AD是△ABC的高的图形是( )
A.
B.
C.
D.
【分析】根据过三角形的顶点向对边作垂线,顶点和垂足之间的线段叫做三角形的高线解答.
【解答】解:△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.
故选:D.
5.冠状病毒因在显微镜下观察类似王冠而得名,新型冠状病毒是以前从未在人体中发现的冠状病毒,新型冠状病毒的半径约是0.000000045米,将数0.000000045用科学记数法表示为( )
A.4.5×108
B.45×10﹣7
C.4.5×10﹣8
D.0.45×10﹣9
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.000000045=4.5×10﹣8,
故选:C.
6.下列各式由左边到右边的变形中,是分解因式的为( )
A.10x2﹣5x=5x?2x﹣5x
B.a(x+y)=ax+ay
C.x2﹣4x+4=(x﹣2)2
D.x2﹣16+3x=(x﹣4)(x+4)+3x
【分析】根据因式分解是把一个多项式转化成几个整式乘积的形式,可得答案.
【解答】解:A、不符合因式分解的定义,不是因式分解,故此选项不符合题意;
B、是整式的乘法,不是因式分解,故此选项不符合题意;
C、符合因式分解的定义,是因式分解,故此选项符合题意;
D、不符合因式分解的定义,不是因式分解,故此选项不符合题意;
故选:C.
7.下列说法中,正确的是( )
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线垂直
D.同旁内角互补
【分析】根据线段、垂线、同旁内角的相关概念和性质判断.
【解答】解:A、两点之间的距离是指两点间的线段长度,而不是线段本身,原说法错误,故此选项不符合题意;
B、在同一平面内,与同一条直线垂直的两条直线平行,原说法错误,故此选项不符合题意;
C、同一平面内,过一点有且只有一条直线与已知直线垂直,原说法正确,故此选项符合题意;
D、只有两直线平行,同旁内角才互补,原说法错误,故此选项不符合题意.
故选:C.
8.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
【分析】利用公因式的确定方法可得答案.
【解答】解:多项式8a3b2+12a3bc﹣4a2b中各项的公因式是4a2b,
故选:C.
9.若关于x的不等式组无解,则m的取值范围是( )
A.m>4
B.m<4
C.m≥4
D.m≤4
【分析】根据求不等式组解集的规律得出答案即可.
【解答】解:∵关于x的不等式组无解,
∴m≤4,
故选:D.
10.如果将一副三角板按如图方式叠放,那么∠1的度数是( )
A.90°
B.100°
C.105°
D.135°
【分析】直接利用一副三角板的内角度数,再结合三角形外角的性质得出答案.
【解答】解:如图所示:由题意可得,∠2=90°﹣45°=45°,
则∠1=∠2+60°=45°+60°=105°.
故选:C.
11.(2分)若方程组的解中x+y=16,则k等于( )
A.15
B.18
C.16
D.17
【分析】根据题意得,解三元一次方程组即可求得k的值.
【解答】解:由题意得,
①+③得:4x=4k+11④,
①×6+②得:20x=25k﹣30,即4x=5k﹣6⑤,
⑤﹣④得:k=17,
故选:D.
12.(2分)已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0
B.1
C.2
D.3
【分析】首先把a2+b2+c2﹣ab﹣ac﹣bc化为2(a2+b2+c2﹣ab﹣ac﹣bc)÷2,再应用完全平方公式,可得:2(a2+b2+c2﹣ab﹣ac﹣bc)÷2=[(a﹣b)2+(b﹣c)2+(c﹣a)2]÷2,然后把a、b、c的值代入,求出算式的值是多少即可.
【解答】解:∵a=2019x+2018,b=2019x+2019,c=2019x+2020,
∴a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,
∴a2+b2+c2﹣ab﹣ac﹣bc
=2(a2+b2+c2﹣ab﹣ac﹣bc)÷2
=[(a﹣b)2+(b﹣c)2+(c﹣a)2]÷2
=[(﹣1)2+(﹣1)2+22]÷2
=6÷2
=3
故选:D.
13.(2分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
【分析】直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;作出一个直角三角形的高线进行判断,就可以得到.
【解答】解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.
故选:C.
14.(2分)如图,把图1中的①部分剪下来,恰好能拼在②的位置处,构成图2中的图形,形成一个从边长为a的大正方形中剪掉一个边长为b的小正方形.根据图形的变化过程写出的一个正确的等式是( )
A.(a﹣b)=a2﹣2ab+b2
B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣b2
D.(a+b)(a﹣b)=a2﹣b2
【分析】根据面积相等,列出关系式即可.
【解答】解:由题意这两个图形的面积相等,
则(a+b)(a﹣b)=a2﹣b2.
故选:D.
15.(2分)将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
【分析】分三种情况讨论,即可得到这两个三角形不可能都是锐角三角形.
【解答】解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:A.
16.(2分)如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移5个单位长度就得到了另一直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )
①AC∥DF;
②HE=5;
③CF=5;
④四边形DHCF的面积为32.5.
A.1个
B.2个
C.3个
D.4个
【分析】首先由平移的性质可得:S△ABC=S△DEF,AB=DE=8,继而可得S四边形DHCF=S梯形ABEH,然后可求得四边形DHCF的面积.
【解答】解:由平移的性质可得AC∥DF,AB=DE=8,
∵DH=3,
∴HE=DE﹣DH=8﹣3=5,CF=BE=5,S△ABC=S△DEF,
∴S四边形DHCF=S梯形ABEH=(EH+AB)?BE=×(5+8)×5=,
故①②③④都正确,
故选:D.
二、填空题(本大题共4个小题,每小题3分,共12分)
17.若实数a、b满足:a+b=6,a﹣b=10,则2a2﹣2b2= 120 .
【分析】将所求式子变形,然后根据a+b=6,a﹣b=10,即可求出所求式子的值.
【解答】解:2a2﹣2b2
=2(a2﹣b2)
=2(a+b)(a﹣b),
∵a+b=6,a﹣b=10,
∴原式=2×6×10=120,
故答案为:120.
18.如图,在三角形ABC中,AC=5,BC=6,BC边上的高AD=4,若点P在边AC上(不与点A,C重合)移动,则线段BP最短时的长为 .
【分析】根据点到直线的连线中,垂线段最短,得到当BP垂直于AC时,BP的长最小,利用面积法即可求出此时BP的长.
【解答】解:根据垂线段最短可知,当BP⊥AC时,BP最短,
∵S△ABC=×BC×AD=×AC×BP,
∴6×4=5BP,
∴PB=,
即BP最短时的值为:.
故答案为:.
19.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 7 张C类卡片.
【分析】用长乘以宽,列出算式,根据多项式乘以多项式的运算法则展开,然后根据A、B、C类卡片的形状可得答案.
【解答】解:∵(3a+b)(a+2b)
=3a2+6ab+ab+2b2
=3a2+7ab+2b2,
∴若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要A类3张,B类2张,C类7张.
故答案为:7.
20.如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为 68° .
【分析】如图,延长DC交BG于M.由题意可以假设∠DCF=∠GCF=x,∠CGE=∠MGE=y.构建方程组证明∠GMC=2∠E即可解决问题.
【解答】解:如图,延长DC交BG于M.由题意可以假设∠DCF=∠GCF=x,∠CGE=∠MGE=y.
则有,
①﹣②×2可得:∠GMC=2∠E,
∵∠E=34°,
∴∠GMC=68°,
∵AB∥CD,
∴∠GMC=∠B=68°,
故答案为68°.
三、解答题,写出必要的文字说明,证明过程或演算步骤(本大题共6个小题,共66分)
21.(15分)计算题
(1)运用整式乘法公式进行计算:2018×2022﹣20202;
(2)计算:﹣1﹣2020(2020﹣π)°﹣(﹣2)﹣3;
(3)(2+3x)(﹣2+3x)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
【分析】(1)根据2018=2020﹣2和2022=2020+2变形,再利用平方差公式计算;
(2)利用负整数指数幂的公式和零指数幂的值进行计算;
(3)利用平方差公式和完全平方差公式化简求值.
【解答】解:(1)原式=(2020﹣2)(2020+2)﹣20202
=20202﹣22﹣20202
=﹣4;
(2)原式=﹣1×1﹣()
=﹣1+
=﹣;
(3)原式=9x2﹣4﹣5x2+5x﹣4x2+4x﹣1
=9x﹣5,
∵x=﹣,
∴9x﹣5=9×(﹣)﹣5=﹣8.
22.(8分)因式分解
(1)4m2﹣1;
(2)3a2﹣6a+3.
【分析】(1)直接用平方差公式分解即可;
(2)先提出公因式3,再套用完全平方公式.
【解答】解:(1)原式=(2m)2﹣1
=(2m+1)(2m﹣1);
(2)原式=3(a2﹣2a+1)
=3(a﹣1)2.
23.(9分)如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
【分析】根据平行线的判定解答即可.
【解答】证明:过点C作CF∥AB,
∵CF∥DE,
∴∠A+∠ACF=180°,
∵∠A+∠ACD+∠D=360°,
∴∠D+∠DCF=180°,
∴CF∥DE,
∴AB∥DE.
24.(10分)在防控新型冠状病毒期间,甲、乙两个服装厂都接到了制做同一种型号的医用防护服任务,已知甲、乙两个服装厂每天共制做这种防护服100套,甲服装厂15天与乙服装厂10天制做的防护服套数相同.
(1)求甲、乙两个服装厂每天各制做多少套这种防护服.
(2)现有3000套这种防护服的制做任务,要求不超过25天完成,若乙服装厂每天多做8套,那么甲服装厂每天至少多做多少套?
【分析】(1)设甲服装厂每天制做x套防护服,则乙服装厂每天制做(100﹣x)套防护服,根据“甲服装厂15天与乙服装厂10天制做的防护服套数相同”列出方程并解答;
(2)设甲服装厂每天多做m套,根据“不超过25天完成”列出不等式并解答.
【解答】解:(1)设甲服装厂每天制做x套防护服,则乙服装厂每天制做(100﹣x)套防护服,依题意有
15x=10(100﹣x),
解得x=40,
则100﹣x=100﹣40=60.
故甲服装厂每天制做40套防护服,乙服装厂每天制做60套防护服;
(2)设甲服装厂每天多做m套,依题意有
25(100+8+m)≥3000,
解得m≥12.
故甲服装厂每天至少多做12套.
25.(12分)阅读材料:
如果x是一个有理数,我们把不超过x的最大整数记作【x】.
例如,【3.2】=3,【5】=5,【﹣2.1】=﹣3.
那么,x=【x】+a,其中0≤a<1.
例如,3.2=【3.2】+0.2,5=【5】+0,﹣2.1=【﹣2.1】+0.9.
请你解决下列问题:
(1)【4.8】= 4 ,【﹣6.5】= ﹣7 ;
(2)如果x=【3】,那么x的取值范围是
3≤x<4 ;
(3)如果【5x﹣2】=3x+1,那么x的值是
.
【分析】(1)根据新定义直接求解;
(2)根据[x]表示不超过x的最大整数的定义即可求解;
(3)根据[x]表示不超过x的最大整数的定义得:3x+1≤5x﹣2<3x+2,且3x+1是整数,计算可得结论;
(4)根据4a=[x]+1,表示a,再根据a的范围建立不等式x值.
【解答】解:(1)[4.8]=4,[﹣6.5]=﹣7.
故答案为:4,﹣7.
(2)如果[x]=3.
那么x的取值范围是3≤x<4.
故答案为:3≤x<4.
(3)如果[5x﹣2]=3x+1,
那么3x+1≤5x﹣2<3x+2.
解得:≤x<2.
∵3x+1是整数.
∴x=.
故答案为:.
26.(12分)探索三角形的内角与外角平分线:
(1)已知,如图1,在△ABC中,两内角平分线,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC= 115° ;此时∠A与∠BOC有怎样的关系,试说明理由.
(2)已知,如图2,在△ABC中,一内角平分线BO平分∠ABC,一外角平分线CO平分∠ACE,若∠A=50°,则∠BOC= 25° ;此时∠A与∠BOC有怎样的关系,试说明理由.
(3)已知,如图3,在△ABC中,∠ABC、∠ACB的外角平分线OB、OC相交于点O,若∠A=50°,则∠BOC= 65° ;此时∠A与∠BOC有怎样的关系(不需说明理由)
图1中:关系式: ∠BOC=90°+∠A ,理由: 略 ;
图2中:关系式: ∠BOC=∠A ,理由: 略 ;
图3中:关系式: ∠BOC=90°﹣∠A ,理由: 略 .
【分析】(1)根据三角形内角和定理得到∠BOC=180°﹣∠OBC﹣∠OCB,则2∠BOC=360°﹣2∠OBC﹣2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°﹣∠ABC﹣∠ACB,易得∠BOC=90°+∠A.
(2)根据角平分线的定义得∠ACE=2∠OCE,∠ABC=2∠OBC,由三角形外角的性质有∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,则2∠BOC+2∠OBC=∠ABC+∠A,即可得到∠BOC=∠A;
(3)根据三角形内角和定理和外角性质可得到∠BOC=90°﹣∠A.
【解答】解:(1)∠BOC=90°+∠A.理由如下:
∵∠BOC=180°﹣∠OBC﹣∠OCB,
∴2∠BOC=360°﹣2∠OBC﹣2∠OCB,
而BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+∠A.
当∠A=50°,∠BOC=115°;
(2)∠BOC=∠A.理由如下:
∵∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,
而BO平分∠ABC,CO平分∠ACE,
∴∠ACE=2∠OCE,∠ABC=2∠OBC,
∴2∠BOC+2∠OBC=∠ABC+∠A,
∴2∠BOC=∠A,
即∠BOC=∠A.
当∠A=50°,∠BOC=25°;
(3)∠BOC=90°﹣∠A.
当∠A=50°,∠BOC=65°.
一、单选题(本大题共16个小题,1-10小题,每小题3分;11-16小题,每小题3分;共42分,在每小题给出的四个选项中,只有一项符合题目要求)
1.已知x,y满足方程组,则无论m取何值,x,y恒有关系式是( )
A.x+y=1
B.x+y=﹣1
C.x+y=9
D.x+y=﹣9
2.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
3.不等式组的解集在数轴上表示如图所示,则该不等式组可能为( )
A.
B.
C.
D.
4.下列各组图形中,AD是△ABC的高的图形是( )
A.
B.
C.
D.
5.冠状病毒因在显微镜下观察类似王冠而得名,新型冠状病毒是以前从未在人体中发现的冠状病毒,新型冠状病毒的半径约是0.000000045米,将数0.000000045用科学记数法表示为( )
A.4.5×108
B.45×10﹣7
C.4.5×10﹣8
D.0.45×10﹣9
6.下列各式由左边到右边的变形中,是分解因式的为( )
A.10x2﹣5x=5x?2x﹣5x
B.a(x+y)=ax+ay
C.x2﹣4x+4=(x﹣2)2
D.x2﹣16+3x=(x﹣4)(x+4)+3x
7.下列说法中,正确的是( )
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线垂直
D.同旁内角互补
8.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
9.若关于x的不等式组无解,则m的取值范围是( )
A.m>4
B.m<4
C.m≥4
D.m≤4
10.如果将一副三角板按如图方式叠放,那么∠1的度数是( )
A.90°
B.100°
C.105°
D.135°
11.(2分)若方程组的解中x+y=16,则k等于( )
A.15
B.18
C.16
D.17
12.(2分)已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0
B.1
C.2
D.3
13.(2分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
14.(2分)如图,把图1中的①部分剪下来,恰好能拼在②的位置处,构成图2中的图形,形成一个从边长为a的大正方形中剪掉一个边长为b的小正方形.根据图形的变化过程写出的一个正确的等式是( )
A.(a﹣b)=a2﹣2ab+b2
B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣b2
D.(a+b)(a﹣b)=a2﹣b2
15.(2分)将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
16.(2分)如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移5个单位长度就得到了另一直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )
①AC∥DF;
②HE=5;
③CF=5;
④四边形DHCF的面积为32.5.
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共4个小题,每小题3分,共12分)
17.若实数a、b满足:a+b=6,a﹣b=10,则2a2﹣2b2=
.
18.如图,在三角形ABC中,AC=5,BC=6,BC边上的高AD=4,若点P在边AC上(不与点A,C重合)移动,则线段BP最短时的长为
.
19.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要
张C类卡片.
20.如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为
.
三、解答题,写出必要的文字说明,证明过程或演算步骤(本大题共6个小题,共66分)
21.(15分)计算题
(1)运用整式乘法公式进行计算:2018×2022﹣20202;
(2)计算:﹣1﹣2020(2020﹣π)°﹣(﹣2)﹣3;
(3)(2+3x)(﹣2+3x)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
22.(8分)因式分解
(1)4m2﹣1;
(2)3a2﹣6a+3.
23.(9分)如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
24.(10分)在防控新型冠状病毒期间,甲、乙两个服装厂都接到了制做同一种型号的医用防护服任务,已知甲、乙两个服装厂每天共制做这种防护服100套,甲服装厂15天与乙服装厂10天制做的防护服套数相同.
(1)求甲、乙两个服装厂每天各制做多少套这种防护服.
(2)现有3000套这种防护服的制做任务,要求不超过25天完成,若乙服装厂每天多做8套,那么甲服装厂每天至少多做多少套?
25.(12分)阅读材料:
如果x是一个有理数,我们把不超过x的最大整数记作【x】.
例如,【3.2】=3,【5】=5,【﹣2.1】=﹣3.
那么,x=【x】+a,其中0≤a<1.
例如,3.2=【3.2】+0.2,5=【5】+0,﹣2.1=【﹣2.1】+0.9.
请你解决下列问题:
(1)【4.8】=
,【﹣6.5】=
;
(2)如果x=【3】,那么x的取值范围是
;
(3)如果【5x﹣2】=3x+1,那么x的值是
.
26.(12分)探索三角形的内角与外角平分线:
(1)已知,如图1,在△ABC中,两内角平分线,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=
;此时∠A与∠BOC有怎样的关系,试说明理由.
(2)已知,如图2,在△ABC中,一内角平分线BO平分∠ABC,一外角平分线CO平分∠ACE,若∠A=50°,则∠BOC=
;此时∠A与∠BOC有怎样的关系,试说明理由.
(3)已知,如图3,在△ABC中,∠ABC、∠ACB的外角平分线OB、OC相交于点O,若∠A=50°,则∠BOC=
;此时∠A与∠BOC有怎样的关系(不需说明理由)
图1中:关系式:
,理由:
;
图2中:关系式:
,理由:
;
图3中:关系式:
,理由:
.
2020-2021学年河北省沧州市沧县等五县联考七年级(下)期末数学试卷
参考答案与试题解析
一、单选题(本大题共16个小题,1-10小题,每小题3分;11-16小题,每小题3分;共42分,在每小题给出的四个选项中,只有一项符合题目要求)
1.已知x,y满足方程组,则无论m取何值,x,y恒有关系式是( )
A.x+y=1
B.x+y=﹣1
C.x+y=9
D.x+y=﹣9
【分析】由方程组消去m,得到一个关于x,y的方程,化简这个方程即可.
【解答】解:由方程组,
有y﹣5=m
∴将上式代入x+m=4,
得到x+(y﹣5)=4,
∴x+y=9.
故选:C.
2.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
【分析】根据不等式的性质解答.
【解答】解:A、若m=3,n=﹣2,则2m>3n,故不符合题意.
B、若m>n,则2+m>2+n,故符合题意.
C、若m>n,则2﹣m<2﹣n,故不符合题意.
D、若m>n,则>,故不符合题意.
故选:B.
3.不等式组的解集在数轴上表示如图所示,则该不等式组可能为( )
A.
B.
C.
D.
【分析】先根据在数轴上表示不等式解集的方法得出该不等式组的解集,再找出符合条件的不等式组即可.
【解答】解:由数轴上表示不等式解集的方法可知,该不等式组的解集为:﹣1<x≤2,
A.的解集是:﹣<x≤2,故本选项不合题意;
B.的解集是:﹣1<x≤2,故本选项符合题意;
C.无解,故本选项不合题意;
D.的解集是:x>2,故本选项不合题意;
故选:B.
4.下列各组图形中,AD是△ABC的高的图形是( )
A.
B.
C.
D.
【分析】根据过三角形的顶点向对边作垂线,顶点和垂足之间的线段叫做三角形的高线解答.
【解答】解:△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.
故选:D.
5.冠状病毒因在显微镜下观察类似王冠而得名,新型冠状病毒是以前从未在人体中发现的冠状病毒,新型冠状病毒的半径约是0.000000045米,将数0.000000045用科学记数法表示为( )
A.4.5×108
B.45×10﹣7
C.4.5×10﹣8
D.0.45×10﹣9
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.000000045=4.5×10﹣8,
故选:C.
6.下列各式由左边到右边的变形中,是分解因式的为( )
A.10x2﹣5x=5x?2x﹣5x
B.a(x+y)=ax+ay
C.x2﹣4x+4=(x﹣2)2
D.x2﹣16+3x=(x﹣4)(x+4)+3x
【分析】根据因式分解是把一个多项式转化成几个整式乘积的形式,可得答案.
【解答】解:A、不符合因式分解的定义,不是因式分解,故此选项不符合题意;
B、是整式的乘法,不是因式分解,故此选项不符合题意;
C、符合因式分解的定义,是因式分解,故此选项符合题意;
D、不符合因式分解的定义,不是因式分解,故此选项不符合题意;
故选:C.
7.下列说法中,正确的是( )
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线垂直
D.同旁内角互补
【分析】根据线段、垂线、同旁内角的相关概念和性质判断.
【解答】解:A、两点之间的距离是指两点间的线段长度,而不是线段本身,原说法错误,故此选项不符合题意;
B、在同一平面内,与同一条直线垂直的两条直线平行,原说法错误,故此选项不符合题意;
C、同一平面内,过一点有且只有一条直线与已知直线垂直,原说法正确,故此选项符合题意;
D、只有两直线平行,同旁内角才互补,原说法错误,故此选项不符合题意.
故选:C.
8.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
【分析】利用公因式的确定方法可得答案.
【解答】解:多项式8a3b2+12a3bc﹣4a2b中各项的公因式是4a2b,
故选:C.
9.若关于x的不等式组无解,则m的取值范围是( )
A.m>4
B.m<4
C.m≥4
D.m≤4
【分析】根据求不等式组解集的规律得出答案即可.
【解答】解:∵关于x的不等式组无解,
∴m≤4,
故选:D.
10.如果将一副三角板按如图方式叠放,那么∠1的度数是( )
A.90°
B.100°
C.105°
D.135°
【分析】直接利用一副三角板的内角度数,再结合三角形外角的性质得出答案.
【解答】解:如图所示:由题意可得,∠2=90°﹣45°=45°,
则∠1=∠2+60°=45°+60°=105°.
故选:C.
11.(2分)若方程组的解中x+y=16,则k等于( )
A.15
B.18
C.16
D.17
【分析】根据题意得,解三元一次方程组即可求得k的值.
【解答】解:由题意得,
①+③得:4x=4k+11④,
①×6+②得:20x=25k﹣30,即4x=5k﹣6⑤,
⑤﹣④得:k=17,
故选:D.
12.(2分)已知a=2019x+2018,b=2019x+2019,c=2019x+2020,则代数式a2+b2+c2﹣ab﹣ac﹣bc的值为( )
A.0
B.1
C.2
D.3
【分析】首先把a2+b2+c2﹣ab﹣ac﹣bc化为2(a2+b2+c2﹣ab﹣ac﹣bc)÷2,再应用完全平方公式,可得:2(a2+b2+c2﹣ab﹣ac﹣bc)÷2=[(a﹣b)2+(b﹣c)2+(c﹣a)2]÷2,然后把a、b、c的值代入,求出算式的值是多少即可.
【解答】解:∵a=2019x+2018,b=2019x+2019,c=2019x+2020,
∴a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,
∴a2+b2+c2﹣ab﹣ac﹣bc
=2(a2+b2+c2﹣ab﹣ac﹣bc)÷2
=[(a﹣b)2+(b﹣c)2+(c﹣a)2]÷2
=[(﹣1)2+(﹣1)2+22]÷2
=6÷2
=3
故选:D.
13.(2分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
【分析】直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;作出一个直角三角形的高线进行判断,就可以得到.
【解答】解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.
故选:C.
14.(2分)如图,把图1中的①部分剪下来,恰好能拼在②的位置处,构成图2中的图形,形成一个从边长为a的大正方形中剪掉一个边长为b的小正方形.根据图形的变化过程写出的一个正确的等式是( )
A.(a﹣b)=a2﹣2ab+b2
B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣b2
D.(a+b)(a﹣b)=a2﹣b2
【分析】根据面积相等,列出关系式即可.
【解答】解:由题意这两个图形的面积相等,
则(a+b)(a﹣b)=a2﹣b2.
故选:D.
15.(2分)将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
【分析】分三种情况讨论,即可得到这两个三角形不可能都是锐角三角形.
【解答】解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:A.
16.(2分)如图,是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移5个单位长度就得到了另一直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )
①AC∥DF;
②HE=5;
③CF=5;
④四边形DHCF的面积为32.5.
A.1个
B.2个
C.3个
D.4个
【分析】首先由平移的性质可得:S△ABC=S△DEF,AB=DE=8,继而可得S四边形DHCF=S梯形ABEH,然后可求得四边形DHCF的面积.
【解答】解:由平移的性质可得AC∥DF,AB=DE=8,
∵DH=3,
∴HE=DE﹣DH=8﹣3=5,CF=BE=5,S△ABC=S△DEF,
∴S四边形DHCF=S梯形ABEH=(EH+AB)?BE=×(5+8)×5=,
故①②③④都正确,
故选:D.
二、填空题(本大题共4个小题,每小题3分,共12分)
17.若实数a、b满足:a+b=6,a﹣b=10,则2a2﹣2b2= 120 .
【分析】将所求式子变形,然后根据a+b=6,a﹣b=10,即可求出所求式子的值.
【解答】解:2a2﹣2b2
=2(a2﹣b2)
=2(a+b)(a﹣b),
∵a+b=6,a﹣b=10,
∴原式=2×6×10=120,
故答案为:120.
18.如图,在三角形ABC中,AC=5,BC=6,BC边上的高AD=4,若点P在边AC上(不与点A,C重合)移动,则线段BP最短时的长为 .
【分析】根据点到直线的连线中,垂线段最短,得到当BP垂直于AC时,BP的长最小,利用面积法即可求出此时BP的长.
【解答】解:根据垂线段最短可知,当BP⊥AC时,BP最短,
∵S△ABC=×BC×AD=×AC×BP,
∴6×4=5BP,
∴PB=,
即BP最短时的值为:.
故答案为:.
19.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 7 张C类卡片.
【分析】用长乘以宽,列出算式,根据多项式乘以多项式的运算法则展开,然后根据A、B、C类卡片的形状可得答案.
【解答】解:∵(3a+b)(a+2b)
=3a2+6ab+ab+2b2
=3a2+7ab+2b2,
∴若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要A类3张,B类2张,C类7张.
故答案为:7.
20.如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为 68° .
【分析】如图,延长DC交BG于M.由题意可以假设∠DCF=∠GCF=x,∠CGE=∠MGE=y.构建方程组证明∠GMC=2∠E即可解决问题.
【解答】解:如图,延长DC交BG于M.由题意可以假设∠DCF=∠GCF=x,∠CGE=∠MGE=y.
则有,
①﹣②×2可得:∠GMC=2∠E,
∵∠E=34°,
∴∠GMC=68°,
∵AB∥CD,
∴∠GMC=∠B=68°,
故答案为68°.
三、解答题,写出必要的文字说明,证明过程或演算步骤(本大题共6个小题,共66分)
21.(15分)计算题
(1)运用整式乘法公式进行计算:2018×2022﹣20202;
(2)计算:﹣1﹣2020(2020﹣π)°﹣(﹣2)﹣3;
(3)(2+3x)(﹣2+3x)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
【分析】(1)根据2018=2020﹣2和2022=2020+2变形,再利用平方差公式计算;
(2)利用负整数指数幂的公式和零指数幂的值进行计算;
(3)利用平方差公式和完全平方差公式化简求值.
【解答】解:(1)原式=(2020﹣2)(2020+2)﹣20202
=20202﹣22﹣20202
=﹣4;
(2)原式=﹣1×1﹣()
=﹣1+
=﹣;
(3)原式=9x2﹣4﹣5x2+5x﹣4x2+4x﹣1
=9x﹣5,
∵x=﹣,
∴9x﹣5=9×(﹣)﹣5=﹣8.
22.(8分)因式分解
(1)4m2﹣1;
(2)3a2﹣6a+3.
【分析】(1)直接用平方差公式分解即可;
(2)先提出公因式3,再套用完全平方公式.
【解答】解:(1)原式=(2m)2﹣1
=(2m+1)(2m﹣1);
(2)原式=3(a2﹣2a+1)
=3(a﹣1)2.
23.(9分)如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
【分析】根据平行线的判定解答即可.
【解答】证明:过点C作CF∥AB,
∵CF∥DE,
∴∠A+∠ACF=180°,
∵∠A+∠ACD+∠D=360°,
∴∠D+∠DCF=180°,
∴CF∥DE,
∴AB∥DE.
24.(10分)在防控新型冠状病毒期间,甲、乙两个服装厂都接到了制做同一种型号的医用防护服任务,已知甲、乙两个服装厂每天共制做这种防护服100套,甲服装厂15天与乙服装厂10天制做的防护服套数相同.
(1)求甲、乙两个服装厂每天各制做多少套这种防护服.
(2)现有3000套这种防护服的制做任务,要求不超过25天完成,若乙服装厂每天多做8套,那么甲服装厂每天至少多做多少套?
【分析】(1)设甲服装厂每天制做x套防护服,则乙服装厂每天制做(100﹣x)套防护服,根据“甲服装厂15天与乙服装厂10天制做的防护服套数相同”列出方程并解答;
(2)设甲服装厂每天多做m套,根据“不超过25天完成”列出不等式并解答.
【解答】解:(1)设甲服装厂每天制做x套防护服,则乙服装厂每天制做(100﹣x)套防护服,依题意有
15x=10(100﹣x),
解得x=40,
则100﹣x=100﹣40=60.
故甲服装厂每天制做40套防护服,乙服装厂每天制做60套防护服;
(2)设甲服装厂每天多做m套,依题意有
25(100+8+m)≥3000,
解得m≥12.
故甲服装厂每天至少多做12套.
25.(12分)阅读材料:
如果x是一个有理数,我们把不超过x的最大整数记作【x】.
例如,【3.2】=3,【5】=5,【﹣2.1】=﹣3.
那么,x=【x】+a,其中0≤a<1.
例如,3.2=【3.2】+0.2,5=【5】+0,﹣2.1=【﹣2.1】+0.9.
请你解决下列问题:
(1)【4.8】= 4 ,【﹣6.5】= ﹣7 ;
(2)如果x=【3】,那么x的取值范围是
3≤x<4 ;
(3)如果【5x﹣2】=3x+1,那么x的值是
.
【分析】(1)根据新定义直接求解;
(2)根据[x]表示不超过x的最大整数的定义即可求解;
(3)根据[x]表示不超过x的最大整数的定义得:3x+1≤5x﹣2<3x+2,且3x+1是整数,计算可得结论;
(4)根据4a=[x]+1,表示a,再根据a的范围建立不等式x值.
【解答】解:(1)[4.8]=4,[﹣6.5]=﹣7.
故答案为:4,﹣7.
(2)如果[x]=3.
那么x的取值范围是3≤x<4.
故答案为:3≤x<4.
(3)如果[5x﹣2]=3x+1,
那么3x+1≤5x﹣2<3x+2.
解得:≤x<2.
∵3x+1是整数.
∴x=.
故答案为:.
26.(12分)探索三角形的内角与外角平分线:
(1)已知,如图1,在△ABC中,两内角平分线,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC= 115° ;此时∠A与∠BOC有怎样的关系,试说明理由.
(2)已知,如图2,在△ABC中,一内角平分线BO平分∠ABC,一外角平分线CO平分∠ACE,若∠A=50°,则∠BOC= 25° ;此时∠A与∠BOC有怎样的关系,试说明理由.
(3)已知,如图3,在△ABC中,∠ABC、∠ACB的外角平分线OB、OC相交于点O,若∠A=50°,则∠BOC= 65° ;此时∠A与∠BOC有怎样的关系(不需说明理由)
图1中:关系式: ∠BOC=90°+∠A ,理由: 略 ;
图2中:关系式: ∠BOC=∠A ,理由: 略 ;
图3中:关系式: ∠BOC=90°﹣∠A ,理由: 略 .
【分析】(1)根据三角形内角和定理得到∠BOC=180°﹣∠OBC﹣∠OCB,则2∠BOC=360°﹣2∠OBC﹣2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°﹣∠ABC﹣∠ACB,易得∠BOC=90°+∠A.
(2)根据角平分线的定义得∠ACE=2∠OCE,∠ABC=2∠OBC,由三角形外角的性质有∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,则2∠BOC+2∠OBC=∠ABC+∠A,即可得到∠BOC=∠A;
(3)根据三角形内角和定理和外角性质可得到∠BOC=90°﹣∠A.
【解答】解:(1)∠BOC=90°+∠A.理由如下:
∵∠BOC=180°﹣∠OBC﹣∠OCB,
∴2∠BOC=360°﹣2∠OBC﹣2∠OCB,
而BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+∠A.
当∠A=50°,∠BOC=115°;
(2)∠BOC=∠A.理由如下:
∵∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,
而BO平分∠ABC,CO平分∠ACE,
∴∠ACE=2∠OCE,∠ABC=2∠OBC,
∴2∠BOC+2∠OBC=∠ABC+∠A,
∴2∠BOC=∠A,
即∠BOC=∠A.
当∠A=50°,∠BOC=25°;
(3)∠BOC=90°﹣∠A.
当∠A=50°,∠BOC=65°.
同课章节目录
