1 5两点间的距离(备课件14张)2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册)
文档属性
| 名称 | 1 5两点间的距离(备课件14张)2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览






文档简介
1.5 两点间的距离
学习目标
1.掌握平面上两点间的距离公式、中点坐标公式;
2.能运用距离公式、中点坐标公式解决一些简单的问题;
3.理解坐标法的意义,并会用坐标法研究问题.
情景引入
已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法一:证明两组对边分别平行
方法二:证明一组对边平行且相等
方法三:证明两组对边分别相等
方法四:证明对角线互相平分
问题:如何求解AB、CD的距离?
在x轴上,已知点P1(x1,0)和P2(x2,0),那么点P1和P2的距离为多少?
在y轴上,已知点P1(0,y1)和P2(0,y2),那么点P1和P2的距离为多少?
|P1P2|=|x1-x2|
|P1P2|=|y1-y2|
x
y
o
P1(x1,0)
P2(x2,0)
x
y
o
P2(0,y2)
P1(0,y1)
合作探究
已知x轴上一点P1(x0,0)和y轴上一点P2(0,y0),那么点P1和P2的距离为多少?
x
y
o
P1
P2
已知平面上两点P1(x1,y1)和P2(x2,y2),利用上述方法求点P1和P2的距离
x
y
o
P1
P2
M
y1=y2
?
数学建构
例1、已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法一:证明两组对边分别平行
方法二:证明一组对边平行且相等
方法三:证明两组对边分别相等
方法四:证明对角线互相平分
数学应用
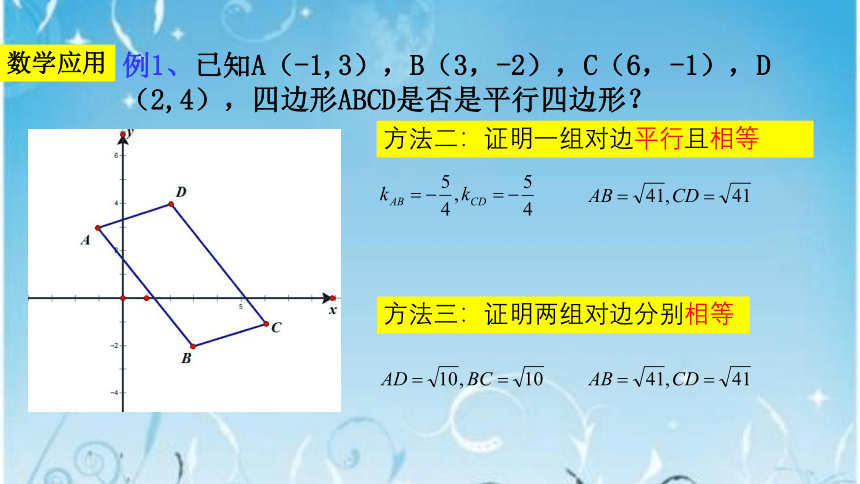
例1、已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法二:证明一组对边平行且相等
方法三:证明两组对边分别相等
数学应用
例1、已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法四:证明对角线互相平分
数学应用
分析:求出BD中点,求出AC中点,
中点坐标一样,即可证明平分
数学建构
?
?
?
数学应用
例3.△ABC的两个顶点为B(2,1),C(-2,3),求BC边的垂直平分线的方程.
解 因为B(2,1),C(-2,3),线段BC的中点坐标是(0,2),
所以BC边的垂直平分线方程是y-2=2(x-0),整理得2x-y+2=0.
数学应用
1、平面上P1(x1,y1),P2(x2,y2)两点间的距离:
2、平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0)
课堂小结
1.已知M(2,1),N(-1,5),则MN等于
√
2.若三角形的顶点分别为A(2,-3),B(-2,-5),C(6,4),则AB边上的中线长为___.
10
达标测试
3.若△ABC的顶点A(-5,0),B(3,-2),C(1,2),则经过AB,BC两边中点的直线方程为
A.3x-y-2=0 B.x-3y-4=0 C.x-3y-2=0 D.3x-y-4=0
√
4.在x轴上到A(-4,3)和B(2,6)两点的距离相等的点P的坐标为_______
?
谢谢!
学习目标
1.掌握平面上两点间的距离公式、中点坐标公式;
2.能运用距离公式、中点坐标公式解决一些简单的问题;
3.理解坐标法的意义,并会用坐标法研究问题.
情景引入
已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法一:证明两组对边分别平行
方法二:证明一组对边平行且相等
方法三:证明两组对边分别相等
方法四:证明对角线互相平分
问题:如何求解AB、CD的距离?
在x轴上,已知点P1(x1,0)和P2(x2,0),那么点P1和P2的距离为多少?
在y轴上,已知点P1(0,y1)和P2(0,y2),那么点P1和P2的距离为多少?
|P1P2|=|x1-x2|
|P1P2|=|y1-y2|
x
y
o
P1(x1,0)
P2(x2,0)
x
y
o
P2(0,y2)
P1(0,y1)
合作探究
已知x轴上一点P1(x0,0)和y轴上一点P2(0,y0),那么点P1和P2的距离为多少?
x
y
o
P1
P2
已知平面上两点P1(x1,y1)和P2(x2,y2),利用上述方法求点P1和P2的距离
x
y
o
P1
P2
M
y1=y2
?
数学建构
例1、已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法一:证明两组对边分别平行
方法二:证明一组对边平行且相等
方法三:证明两组对边分别相等
方法四:证明对角线互相平分
数学应用
例1、已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法二:证明一组对边平行且相等
方法三:证明两组对边分别相等
数学应用
例1、已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?
方法四:证明对角线互相平分
数学应用
分析:求出BD中点,求出AC中点,
中点坐标一样,即可证明平分
数学建构
?
?
?
数学应用
例3.△ABC的两个顶点为B(2,1),C(-2,3),求BC边的垂直平分线的方程.
解 因为B(2,1),C(-2,3),线段BC的中点坐标是(0,2),
所以BC边的垂直平分线方程是y-2=2(x-0),整理得2x-y+2=0.
数学应用
1、平面上P1(x1,y1),P2(x2,y2)两点间的距离:
2、平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0)
课堂小结
1.已知M(2,1),N(-1,5),则MN等于
√
2.若三角形的顶点分别为A(2,-3),B(-2,-5),C(6,4),则AB边上的中线长为___.
10
达标测试
3.若△ABC的顶点A(-5,0),B(3,-2),C(1,2),则经过AB,BC两边中点的直线方程为
A.3x-y-2=0 B.x-3y-4=0 C.x-3y-2=0 D.3x-y-4=0
√
4.在x轴上到A(-4,3)和B(2,6)两点的距离相等的点P的坐标为_______
?
谢谢!
