2 1圆的方程(第1课时 圆的标准方程)(备课件22张-)-2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册)
文档属性
| 名称 | 2 1圆的方程(第1课时 圆的标准方程)(备课件22张-)-2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 775.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 18:42:22 | ||
图片预览







文档简介
2.1 圆的方程
第1课时 圆的标准方程
学习目标
1.掌握圆的标准方程,能根据圆心、半径写出圆的标准方程
2.会用待定系数法求圆的标准方程
3.进一步培养学生能用解析法研究几何问题的能力,渗透数形结合思想
情景引入
日出
情景引入
摩天轮
情景引入
荷叶
情景引入
一石激起千层浪
圆
圆是自然界最完美的曲线之一.
复习引入
问题1.平面内,两点确定一条直线,一点和倾斜角也确定一条直线,那么在什么条件下可以确定一个圆呢?
问题2.引入平面直角坐标系,直线可以用一个方程表示,圆也可以用一个方程来表示吗?
合作探究
如何用集合符号语言描述以点C为圆心,r为半径的圆?
思考1:圆可以看成是平面上的一条曲线,在平面几何中,圆是怎样定义的?
圆的定义:平面上到一个定点的距离等于定长的点的集合叫做圆.
C
P
r
M={P||PC|=r}.
圆心-确定圆的位置
半径-确定圆的大小
合作探究
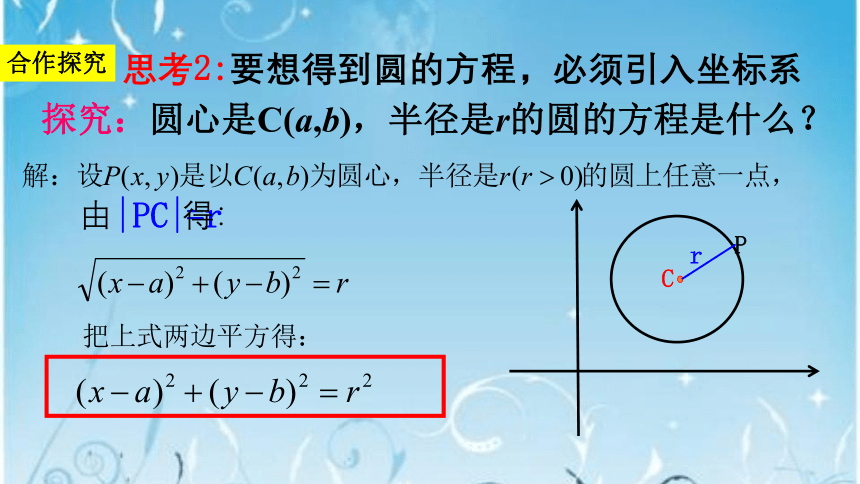
思考2:要想得到圆的方程,必须引入坐标系
C
P
r
|PC|=r
探究:圆心是C(a,b),半径是r的圆的方程是什么?
由 得:
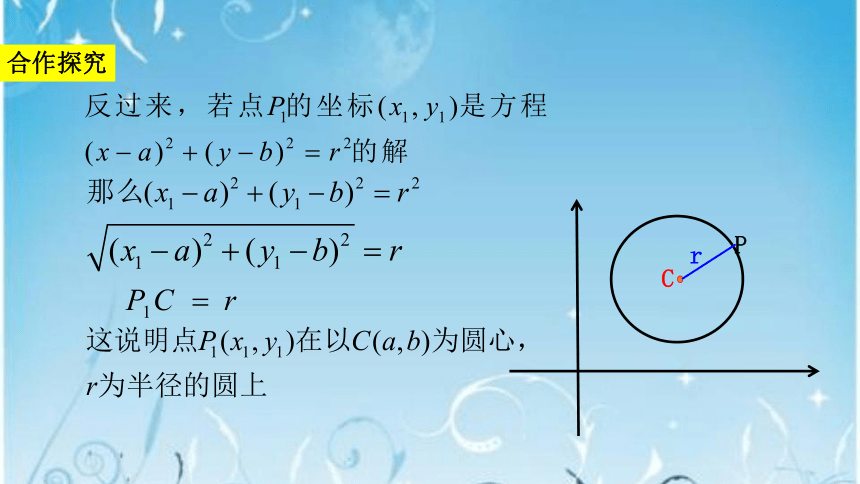
合作探究
C
P
r
数学建构
(x-a) 2 + (y-b) 2 = r2 (r > 0)
特点:
4、若圆心在坐标原点,则圆方程为x2+y2=r2.
当r=1,即x2+y2=1时,称该方程表示的
圆为单位圆.
问题:观察圆的标准方程的特点有哪些?
圆的标准方程:
2、明确给出了圆心坐标和半径.
3、确定圆的方程必须具备三个独立条件,
即a、b、r .
1、是关于x、y的二元二次方程.
概念辨析
判断下列方程是否为圆的方程,如果是,写出下
列各圆的圆心坐标和半径.
(1) (x-1)2+y2=6 (2) (x+1)2-(y-2)2=9
(3)x2+(y+3)2=0 (4)(x+a)2+y2=a2
数学应用
例1(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的标准方程是__ .
解析 ∵AB为直径,
∴AB的中点(1,2)为圆心,
∴该圆的标准方程为
(直接法)
解析∵圆心坐标为(-5,-3),
又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为
(2)与y轴相切于点P,且圆心C 坐标为(-5,-3)的圆的标准方程为__.
(直接法)
数学应用
(待定系数法)
解析:
x
y
O
C
A(1,-1)
B(-1,1)
数学应用
x
y
O
C
A(1,-1)
B(-1,1)
方法二 由几何关系知,圆心在AB的垂直平分线上,
∵AB的中点为(0,0),AB的斜率k=-1,
则AB的垂直平分线为y-0=x-0.
(直接法:几何法)
课堂小结
(1)直接法
根据已知条件,直接求出圆心坐标和圆的半径,然后写出圆的方程.
求解圆的标准方程方法:
(2)待定系数法
①根据题意,设出标准方程;
②根据条件,列关于a,b,r的方程组;
③解出a,b,r,代入标准方程.
数学应用
例2:已知圆D的方程为 (x+1) 2 + (y-1) 2 = 4 ,判断下面的点A(1,1),B(0,1),C(0,3)在圆内、圆上、还是圆外?
x
y
O
D
A(1,1)
B(0,1)
C(0,3)
|DA|=2
|DB|=1
|DC|=
r =2
r =2
r =2
A在圆上
B在圆内
C在圆外
数学建构
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
点M在圆上
CM=r
点M在圆外
CM>r
点M在圆内
CM利用方程判断
数学建构
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
利用方程判断
点M在圆上
CM=r
(x0-a)2+(y0-b)2 r2
点M在圆外
CM>r
(x0-a)2+(y0-b)2 r2
点M在圆内
CM(x0-a)2+(y0-b)2 r2
=
>
<
(1)圆心为C(a,b),半径为r的圆的标准方程为 (x-a)2+(y-b)2=r2
当圆心在原点时 a=b=0,圆的标准方程为:x2+y2=r2
(2)由于圆的标准方程中含有 a, b, r三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程.
(3)会判定点与圆的位置关系.
课堂小结
(2)求圆心为(1,3) ,且和直线3x-4y-7=0相切的圆的标准方程.
解:(2)因为圆和直线3x-4y-7=0相切,
所以圆的半径r = ????×?????????×?????????????????+???????? =????????????,
圆的方程为: (x-1) 2 + (y-3) 2 =????????????????????
?
例2
解:(1)由(m2)2+52=m4+25>24,
∴点P在圆外.
x
y
O
C
M(-1,1).
P.
达标测试
谢谢!
第1课时 圆的标准方程
学习目标
1.掌握圆的标准方程,能根据圆心、半径写出圆的标准方程
2.会用待定系数法求圆的标准方程
3.进一步培养学生能用解析法研究几何问题的能力,渗透数形结合思想
情景引入
日出
情景引入
摩天轮
情景引入
荷叶
情景引入
一石激起千层浪
圆
圆是自然界最完美的曲线之一.
复习引入
问题1.平面内,两点确定一条直线,一点和倾斜角也确定一条直线,那么在什么条件下可以确定一个圆呢?
问题2.引入平面直角坐标系,直线可以用一个方程表示,圆也可以用一个方程来表示吗?
合作探究
如何用集合符号语言描述以点C为圆心,r为半径的圆?
思考1:圆可以看成是平面上的一条曲线,在平面几何中,圆是怎样定义的?
圆的定义:平面上到一个定点的距离等于定长的点的集合叫做圆.
C
P
r
M={P||PC|=r}.
圆心-确定圆的位置
半径-确定圆的大小
合作探究
思考2:要想得到圆的方程,必须引入坐标系
C
P
r
|PC|=r
探究:圆心是C(a,b),半径是r的圆的方程是什么?
由 得:
合作探究
C
P
r
数学建构
(x-a) 2 + (y-b) 2 = r2 (r > 0)
特点:
4、若圆心在坐标原点,则圆方程为x2+y2=r2.
当r=1,即x2+y2=1时,称该方程表示的
圆为单位圆.
问题:观察圆的标准方程的特点有哪些?
圆的标准方程:
2、明确给出了圆心坐标和半径.
3、确定圆的方程必须具备三个独立条件,
即a、b、r .
1、是关于x、y的二元二次方程.
概念辨析
判断下列方程是否为圆的方程,如果是,写出下
列各圆的圆心坐标和半径.
(1) (x-1)2+y2=6 (2) (x+1)2-(y-2)2=9
(3)x2+(y+3)2=0 (4)(x+a)2+y2=a2
数学应用
例1(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的标准方程是__ .
解析 ∵AB为直径,
∴AB的中点(1,2)为圆心,
∴该圆的标准方程为
(直接法)
解析∵圆心坐标为(-5,-3),
又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为
(2)与y轴相切于点P,且圆心C 坐标为(-5,-3)的圆的标准方程为__.
(直接法)
数学应用
(待定系数法)
解析:
x
y
O
C
A(1,-1)
B(-1,1)
数学应用
x
y
O
C
A(1,-1)
B(-1,1)
方法二 由几何关系知,圆心在AB的垂直平分线上,
∵AB的中点为(0,0),AB的斜率k=-1,
则AB的垂直平分线为y-0=x-0.
(直接法:几何法)
课堂小结
(1)直接法
根据已知条件,直接求出圆心坐标和圆的半径,然后写出圆的方程.
求解圆的标准方程方法:
(2)待定系数法
①根据题意,设出标准方程;
②根据条件,列关于a,b,r的方程组;
③解出a,b,r,代入标准方程.
数学应用
例2:已知圆D的方程为 (x+1) 2 + (y-1) 2 = 4 ,判断下面的点A(1,1),B(0,1),C(0,3)在圆内、圆上、还是圆外?
x
y
O
D
A(1,1)
B(0,1)
C(0,3)
|DA|=2
|DB|=1
|DC|=
r =2
r =2
r =2
A在圆上
B在圆内
C在圆外
数学建构
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
点M在圆上
CM=r
点M在圆外
CM>r
点M在圆内
CM
数学建构
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
利用方程判断
点M在圆上
CM=r
(x0-a)2+(y0-b)2 r2
点M在圆外
CM>r
(x0-a)2+(y0-b)2 r2
点M在圆内
CM
=
>
<
(1)圆心为C(a,b),半径为r的圆的标准方程为 (x-a)2+(y-b)2=r2
当圆心在原点时 a=b=0,圆的标准方程为:x2+y2=r2
(2)由于圆的标准方程中含有 a, b, r三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程.
(3)会判定点与圆的位置关系.
课堂小结
(2)求圆心为(1,3) ,且和直线3x-4y-7=0相切的圆的标准方程.
解:(2)因为圆和直线3x-4y-7=0相切,
所以圆的半径r = ????×?????????×?????????????????+???????? =????????????,
圆的方程为: (x-1) 2 + (y-3) 2 =????????????????????
?
例2
解:(1)由(m2)2+52=m4+25>24,
∴点P在圆外.
x
y
O
C
M(-1,1).
P.
达标测试
谢谢!
