3 1 1数系的扩充与复数的概念课件 (22张PPT)---2020-2021学年高二数学人教A版选修2-2第三章
文档属性
| 名称 | 3 1 1数系的扩充与复数的概念课件 (22张PPT)---2020-2021学年高二数学人教A版选修2-2第三章 |

|
|
| 格式 | pptx | ||
| 文件大小 | 499.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 19:54:17 | ||
图片预览






文档简介
3.1.1 数系的扩充与复数的概念
学习目标:
1、理解复数的基本概念
2、理解复数相等的充要条件
3、理解复数的代数表示方法
4、了解数系的扩充过程
学习重点:
复数的概念,复数的代数形式表示.
学习难点:
理解复数的基本概念以及复数相等的充要条件.
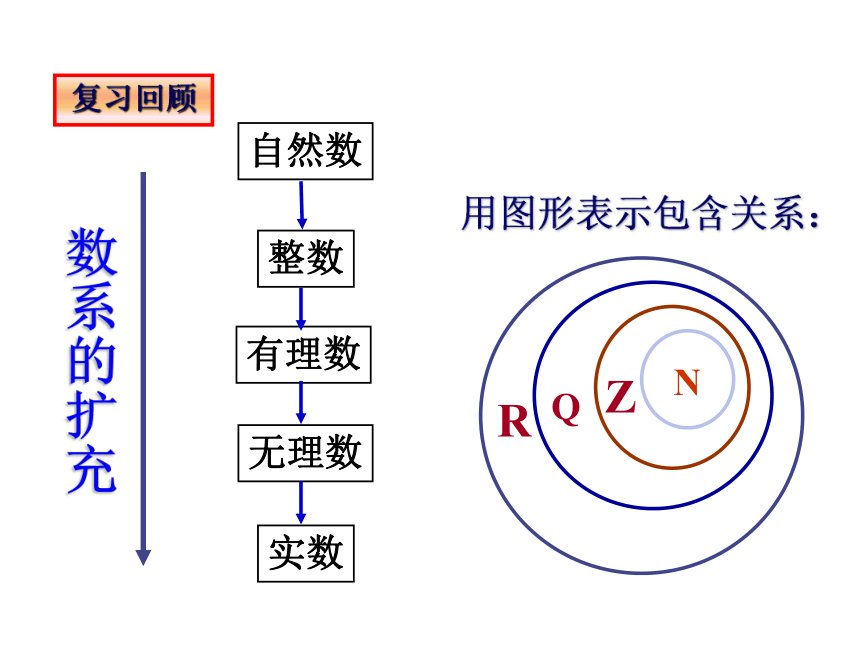
数系的扩充
自然数
整数
有理数
无理数
实数
N
Z
Q
R
用图形表示包含关系:
复习回顾
下列方程在给定数集内有解吗?
N
Z
Q
R
自然数
整数
有理数
实数
?
负整数
分数
无理数
数 系 的 扩 充
减法
除法
开方
?
数系的每一次扩充,解决了在原有数集中运算不能实施的矛盾,且原数集中运算规则在新数集中得到保留.
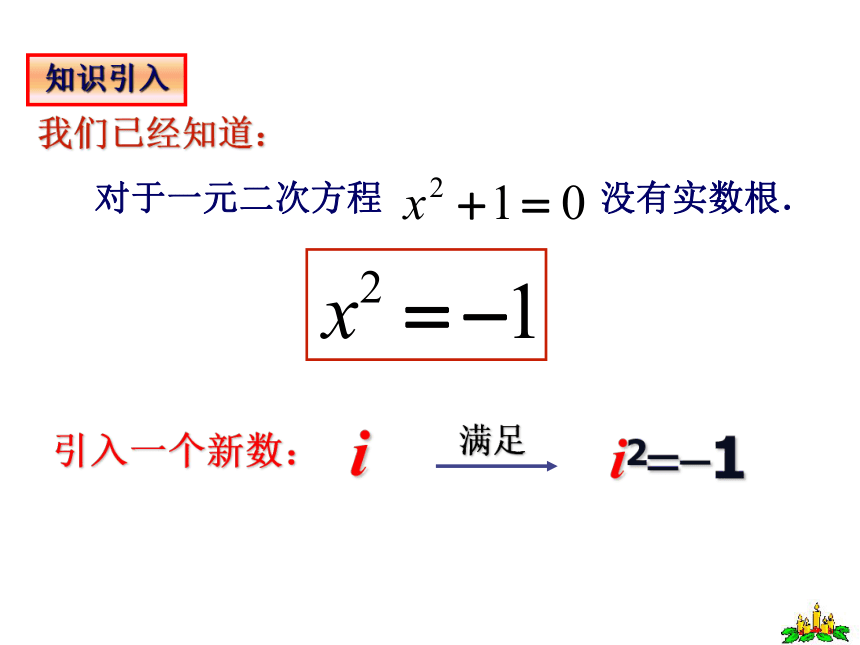
知识引入
对于一元二次方程 没有实数根.
我们已经知道:
满足
引入一个新数:
i
i2??1
引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。
形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集,
一般用字母C表示 .
一、复数的概念
实部
复数的代数形式:
通常用字母 z 表示,即
虚部
其中 称为虚数单位。
复数集C和实数集R之间有什么关系?
讨论?
复数a+bi
(a,b∈R)
复数的分类
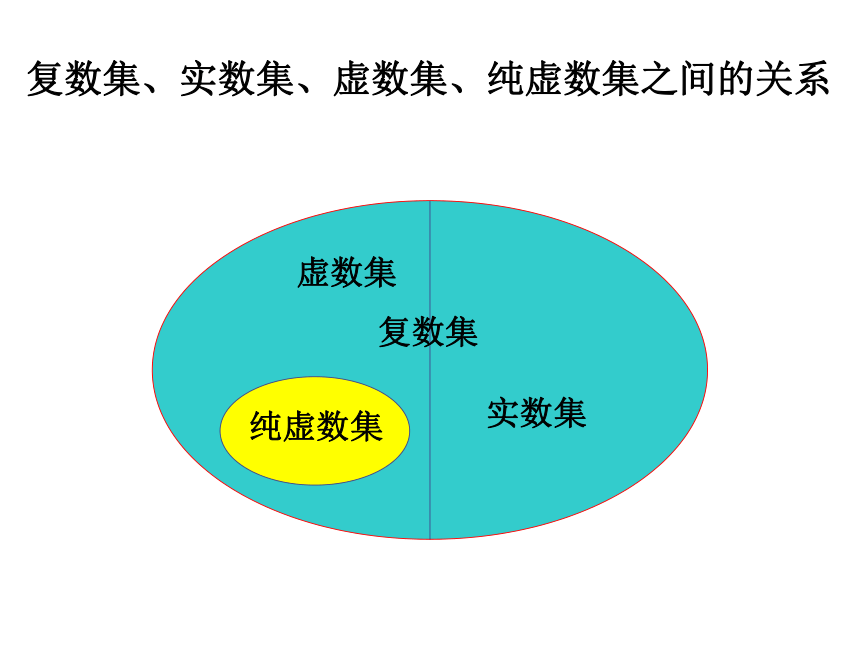
复数集
虚数集
实数集
纯虚数集
复数集、实数集、虚数集、纯虚数集之间的关系
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
二、复数相等的定义
注意:
除了复数的相等之外,还规定:
只有当两个复数都是实数时,它们才能比较大小。
练一练:
说明下列数中,哪些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。
5 +8
0,
实数:
虚数:
纯虚数
实部a
虚部b
0
5 +8
0
0
0
0
0
-1
0
0
3
8
5
i2??1
复数z=a+bi(a,b∈R)
例1 实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
解: (1)当 ,即 时,复数z 是实数.
(2)当 ,即 时,复数z 是虚数.
(3)当
即 时,复数z 是
纯虚数.
变式训练1:实数m 取什么值时,复数
z=(m2-3m-4)+(m2-5m-6)i
(1) 是实数?(2)纯虚数? (3)零?
解:(1)当m2-5m-6=0时,
即m=6或m=-1时,
z为实数
(2)当 时,
m2-3m-4=0
m2-5m-6?0
即m=4时,
z为纯虚数
(3)当 时,
m2-3m-4=0
m2-5m-6=0
即m=-1时,
z为零
例2 已知 ,
其中 求
解:根据复数相等的定义,得方程组
,解得
1.若x,y为实数,且
求x,y.
变式训练2:
x=-3,y=4
2.若(2x2-3x-2)+(x2-5x+6) =0,求实数x的值.
x=2
例3 解方程:
x2-2x+3=0
解:一元二次方程 x2-2x+3=0的判别式
故原方程的解是
i2??1
变式训练3: 解下列方程
(1) x2-x+1=0;
(2) 2x2-x+1=0.
答案:
小结:
1.虚数单位i的引入:
2.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
i2??1
课后作业:
5. 已知 是实数, 是纯虚数,且满足
, 求 、 。
课本习题3.1A组 1、2.
再见!
学习目标:
1、理解复数的基本概念
2、理解复数相等的充要条件
3、理解复数的代数表示方法
4、了解数系的扩充过程
学习重点:
复数的概念,复数的代数形式表示.
学习难点:
理解复数的基本概念以及复数相等的充要条件.
数系的扩充
自然数
整数
有理数
无理数
实数
N
Z
Q
R
用图形表示包含关系:
复习回顾
下列方程在给定数集内有解吗?
N
Z
Q
R
自然数
整数
有理数
实数
?
负整数
分数
无理数
数 系 的 扩 充
减法
除法
开方
?
数系的每一次扩充,解决了在原有数集中运算不能实施的矛盾,且原数集中运算规则在新数集中得到保留.
知识引入
对于一元二次方程 没有实数根.
我们已经知道:
满足
引入一个新数:
i
i2??1
引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。
形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集,
一般用字母C表示 .
一、复数的概念
实部
复数的代数形式:
通常用字母 z 表示,即
虚部
其中 称为虚数单位。
复数集C和实数集R之间有什么关系?
讨论?
复数a+bi
(a,b∈R)
复数的分类
复数集
虚数集
实数集
纯虚数集
复数集、实数集、虚数集、纯虚数集之间的关系
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
二、复数相等的定义
注意:
除了复数的相等之外,还规定:
只有当两个复数都是实数时,它们才能比较大小。
练一练:
说明下列数中,哪些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。
5 +8
0,
实数:
虚数:
纯虚数
实部a
虚部b
0
5 +8
0
0
0
0
0
-1
0
0
3
8
5
i2??1
复数z=a+bi(a,b∈R)
例1 实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
解: (1)当 ,即 时,复数z 是实数.
(2)当 ,即 时,复数z 是虚数.
(3)当
即 时,复数z 是
纯虚数.
变式训练1:实数m 取什么值时,复数
z=(m2-3m-4)+(m2-5m-6)i
(1) 是实数?(2)纯虚数? (3)零?
解:(1)当m2-5m-6=0时,
即m=6或m=-1时,
z为实数
(2)当 时,
m2-3m-4=0
m2-5m-6?0
即m=4时,
z为纯虚数
(3)当 时,
m2-3m-4=0
m2-5m-6=0
即m=-1时,
z为零
例2 已知 ,
其中 求
解:根据复数相等的定义,得方程组
,解得
1.若x,y为实数,且
求x,y.
变式训练2:
x=-3,y=4
2.若(2x2-3x-2)+(x2-5x+6) =0,求实数x的值.
x=2
例3 解方程:
x2-2x+3=0
解:一元二次方程 x2-2x+3=0的判别式
故原方程的解是
i2??1
变式训练3: 解下列方程
(1) x2-x+1=0;
(2) 2x2-x+1=0.
答案:
小结:
1.虚数单位i的引入:
2.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
i2??1
课后作业:
5. 已知 是实数, 是纯虚数,且满足
, 求 、 。
课本习题3.1A组 1、2.
再见!
