1 4充分条件与必要条件(习题课课件 24张)-2021-2022学年高一上学期数学人教A版必修第一册
文档属性
| 名称 | 1 4充分条件与必要条件(习题课课件 24张)-2021-2022学年高一上学期数学人教A版必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 943.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 20:21:19 | ||
图片预览








文档简介
第一章 集合与常用逻辑用语
1.4 充分条件与必要条件
(第2课时)
复习
1、?????????:p是q的充分条件,q是p的必要条件
?????????:p是q的必要条件,q是p的充分条件
2、?????????,?????????:p是q的充要条件
?????????,?????????:p是q的充分不必要条件
?????????,?????????:p是q的必要不充分条件
?????????,?????????:p是q的既不充分也不必要条件
3、判断一个命题为真,要依据定义、定理或常用结论能由条件推出结论成立;判断一个命题为假,只需举反例。
?
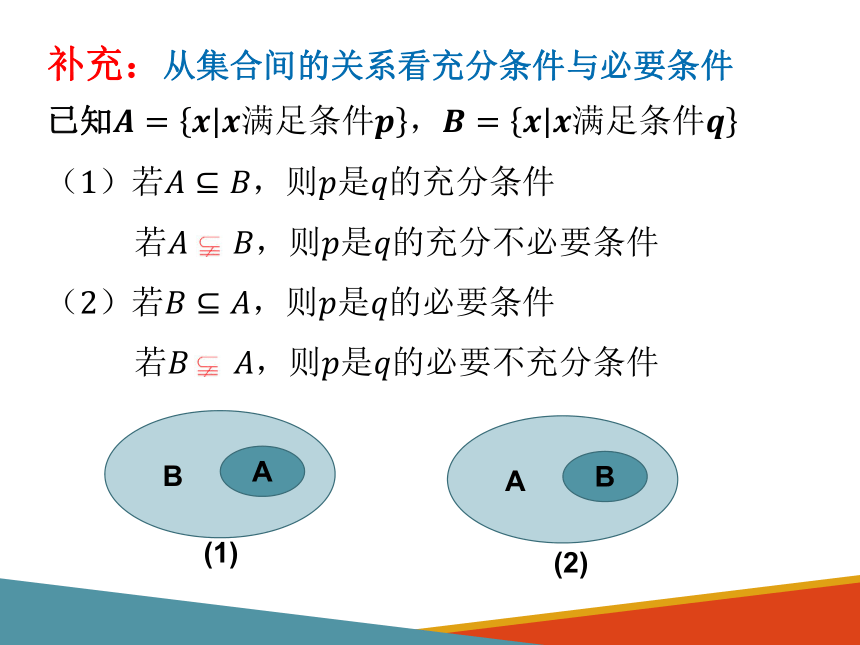
补充:从集合间的关系看充分条件与必要条件
已知????=????????满足条件????,????=????????满足条件????
(1)若?????????,则????是????的充分条件
若??????????????,则????是????的充分不必要条件
(2)若?????????,则????是????的必要条件
若??????????????,则????是????的必要不充分条件
?
B
A
(1)
A
B
(2)
补充:从集合间的关系看充分条件与必要条件
已知????=????????满足条件????,????=????????满足条件????
(3)若????=????,则????,????互为充要条件
(4)若?????????,?????????,则????是????的既不充分也不必要条件
?
A(B)
(3)
A
B
A
B
(4)
简记:
小范围
大范围
?
?
?
?
顺着箭头方向讲是“充分”
逆着箭头方向讲是“必要”
题型一:充要条件的判断
例1 在下列各题中,判断p是q的什么条件(请用“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”回答)
(1)p:????+????(2)p:????????≠????,q:????????+????????≠????
?
p是q的必要不充分条件
p
q
?
?
?
?
p
q
?
?
?
?
p是q的充分不必要条件
(3)p:0(4)p:点?????????????,????????+????在第四象限,q:?????
大范围
小范围
?
?
?
?
p是q的必要不充分条件
点????1?????,2????+6在第四象限,即1?????>02????+6<0,
解得?????
p:?????
小范围
大范围
?
?
?
?
p是q的充分不必要条件
题型技法
充分条件、必要条件、充要条件的判断方法:
1.定义法:判断的三个步骤如下
(1)分清命题的条件和结论;
(2)找推式:判断“p?q”及“q?p”的真假;
(3)确定条件p和结论q的关系.
2.集合法:根据p,q成立时对应的集合之间的包含关系进行判断.
?
巩固训练
1、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空
(1)“????>????”是“?????????????????>0”的 条件;
(2)“点M在直线????=?????上”是“点M到两坐标轴的距离相等”的 条件;
(3)“????=????”是“??????????????????=0”的 条件;
(4)“????+????是无理数”是“????是无理数”的 条件;
(5)“????<5”是“????<3”的 条件;
(6)“四边形的对角线相等”是“四边形为平行四边形”的
条件;
?
必要不充分
充分不必要
充分不必要
充要
必要不充分
既充分也不必要
巩固训练
2、(多选)使不等式?????????????.?????????????. ??????
BD
解析:由题意可知,选项是“?????????即选项所对应的集合是??????????????
?
?
?
?
注意:
在充分、必要条件的判断中,看清设问方式,明确哪个是条件,哪个是结论,然后根据充分条件、必要条件的概念作出准确的判断,从集合的角度判断充分、必要条件,应该准确判断集合间的包含关系。
题型二:根据充分、必要条件,求参数的范围
例2 已知集合????=?????????(1)若????∈????是????∈????成立的一个充分不必要条件,求实数????的取值范围;
?
解:因为????∈????是????∈????成立的一个充分不必要条件,
所以??????????????
?
????+????
?
所以????+????>????,即????>????
所以????的取值范围为????????>????
?
题型二:根据充分、必要条件,求参数的范围
例2 已知集合????=?????????(2)若????∈????是????∈????成立的一个充分不必要条件,求实数????的取值范围;
?
解:因为????∈????是????∈????成立的一个充分不必要条件,
所以???? ????
?
????+????
?
所以?????所以????的取值范围为??????????
题型二:根据充分、必要条件,求参数的范围
例2 已知集合????=?????????(3)若????∈????是????∈????成立的充要条件,求实数????的值;
?
解:因为????∈????是????∈????成立的充要条件,所以????=????
?
所以????+????=????,即????=????
所以实数????的值为2
?
题型技法
依据一个条件是另一个条件的充分条件、必要条件,确定某个参数的取值范围时,先弄清楚条件和结论,再利用集合间的包含关系进行讨论,注意区间端点值的取舍。
巩固训练
1.已知p:?????????>????,q:????≥????,若p是q的充分不必要条件,则实数????的取值范围为( )
????.????????.????≥???? ????.????>????
?
C
解析:由?????????>????得????>????,因为p是q的充分不必要条件,所以????????>???? ????????≥???? ,所以????≥????,故选C
?
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
直线外任意一点到这条直线的垂线段的长度,叫做点到直线的距离。
在连接直线外一点与直线上各点的线段中,垂线段最短。
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
把圆和直线只有一个交点(公共点)的位置关系叫做圆和直线相切,这条直线叫做圆的切线,这个公共点叫做切点。
定理:圆的切线垂直于过切点的半径。
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
分析:设????:????=????,????:直线????与圆????相切
要证????是????的充要条件,只需分别证明充
分性?????????和必要性?????????即可。
?
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
证明:设????:????=????,????:直线????与圆????相切
?
(1)充分性?????????:作????????⊥????于点????,则????????=????,若????=????,则点????在?????上.
在直线????上任取一点????(异于点????).连接????????.在?????????????????????中,????????>????????=????.所以,除点????外直线????上的点都在?????的外部,即直线????与圆????仅有一个公共点,所以直线????与圆????相切.
?
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
(2)必要性?????????:若直线????与圆????相切,不妨设切点为????,则????????⊥????,因此,????=????????=????.
?
证明:设????:????=????,????:直线????与圆????相切
?
由(1)(2)可得????=????是直线????与圆????相切的充要条件.
?
题型技法
关于充要条件命题的证明,一般分为充分性和必要性两个方面进行,其中由条件推出结论就是充分性,由结论推出条件就是必要性。
巩固训练
求证:关于????的方程????????????+????????+????=????有一个根为1的充要条件是????+????+????=????.
?
证明:????:????+????+????=????,????:关于????的方程????????????+????????+????=????有一个根为1
(1)充分性?????????:∵????+????+????=????,∴????=?
巩固训练
求证:关于????的方程????????????+????????+????=????有一个根为1的充要条件是????+????+????=????.
?
证明:????:????+????+????=????,????:关于????的方程????????????+????????+????=????有一个根为1
(2)必要性?????????:∵方程????????????+????????+????=????有一个根为1,∴????=????满足方程????????????+????????+????=????,即????+????+????=????.
由(1)(2)可得,关于????的方程????????????+????????+????=????有一个根为1的充要条件是????+????+????=????.
1.4 充分条件与必要条件
(第2课时)
复习
1、?????????:p是q的充分条件,q是p的必要条件
?????????:p是q的必要条件,q是p的充分条件
2、?????????,?????????:p是q的充要条件
?????????,?????????:p是q的充分不必要条件
?????????,?????????:p是q的必要不充分条件
?????????,?????????:p是q的既不充分也不必要条件
3、判断一个命题为真,要依据定义、定理或常用结论能由条件推出结论成立;判断一个命题为假,只需举反例。
?
补充:从集合间的关系看充分条件与必要条件
已知????=????????满足条件????,????=????????满足条件????
(1)若?????????,则????是????的充分条件
若??????????????,则????是????的充分不必要条件
(2)若?????????,则????是????的必要条件
若??????????????,则????是????的必要不充分条件
?
B
A
(1)
A
B
(2)
补充:从集合间的关系看充分条件与必要条件
已知????=????????满足条件????,????=????????满足条件????
(3)若????=????,则????,????互为充要条件
(4)若?????????,?????????,则????是????的既不充分也不必要条件
?
A(B)
(3)
A
B
A
B
(4)
简记:
小范围
大范围
?
?
?
?
顺着箭头方向讲是“充分”
逆着箭头方向讲是“必要”
题型一:充要条件的判断
例1 在下列各题中,判断p是q的什么条件(请用“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”回答)
(1)p:????+????(2)p:????????≠????,q:????????+????????≠????
?
p是q的必要不充分条件
p
q
?
?
?
?
p
q
?
?
?
?
p是q的充分不必要条件
(3)p:0(4)p:点?????????????,????????+????在第四象限,q:?????
大范围
小范围
?
?
?
?
p是q的必要不充分条件
点????1?????,2????+6在第四象限,即1?????>02????+6<0,
解得?????
p:?????
小范围
大范围
?
?
?
?
p是q的充分不必要条件
题型技法
充分条件、必要条件、充要条件的判断方法:
1.定义法:判断的三个步骤如下
(1)分清命题的条件和结论;
(2)找推式:判断“p?q”及“q?p”的真假;
(3)确定条件p和结论q的关系.
2.集合法:根据p,q成立时对应的集合之间的包含关系进行判断.
?
巩固训练
1、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空
(1)“????>????”是“?????????????????>0”的 条件;
(2)“点M在直线????=?????上”是“点M到两坐标轴的距离相等”的 条件;
(3)“????=????”是“??????????????????=0”的 条件;
(4)“????+????是无理数”是“????是无理数”的 条件;
(5)“????<5”是“????<3”的 条件;
(6)“四边形的对角线相等”是“四边形为平行四边形”的
条件;
?
必要不充分
充分不必要
充分不必要
充要
必要不充分
既充分也不必要
巩固训练
2、(多选)使不等式?????????????.?????????????. ??????
BD
解析:由题意可知,选项是“?????????即选项所对应的集合是??????????????
?
?
?
?
注意:
在充分、必要条件的判断中,看清设问方式,明确哪个是条件,哪个是结论,然后根据充分条件、必要条件的概念作出准确的判断,从集合的角度判断充分、必要条件,应该准确判断集合间的包含关系。
题型二:根据充分、必要条件,求参数的范围
例2 已知集合????=?????????(1)若????∈????是????∈????成立的一个充分不必要条件,求实数????的取值范围;
?
解:因为????∈????是????∈????成立的一个充分不必要条件,
所以??????????????
?
????+????
?
所以????+????>????,即????>????
所以????的取值范围为????????>????
?
题型二:根据充分、必要条件,求参数的范围
例2 已知集合????=?????????(2)若????∈????是????∈????成立的一个充分不必要条件,求实数????的取值范围;
?
解:因为????∈????是????∈????成立的一个充分不必要条件,
所以???? ????
?
????+????
?
所以?????所以????的取值范围为??????????
题型二:根据充分、必要条件,求参数的范围
例2 已知集合????=?????????(3)若????∈????是????∈????成立的充要条件,求实数????的值;
?
解:因为????∈????是????∈????成立的充要条件,所以????=????
?
所以????+????=????,即????=????
所以实数????的值为2
?
题型技法
依据一个条件是另一个条件的充分条件、必要条件,确定某个参数的取值范围时,先弄清楚条件和结论,再利用集合间的包含关系进行讨论,注意区间端点值的取舍。
巩固训练
1.已知p:?????????>????,q:????≥????,若p是q的充分不必要条件,则实数????的取值范围为( )
????.????????.????≥???? ????.????>????
?
C
解析:由?????????>????得????>????,因为p是q的充分不必要条件,所以????????>???? ????????≥???? ,所以????≥????,故选C
?
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
直线外任意一点到这条直线的垂线段的长度,叫做点到直线的距离。
在连接直线外一点与直线上各点的线段中,垂线段最短。
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
把圆和直线只有一个交点(公共点)的位置关系叫做圆和直线相切,这条直线叫做圆的切线,这个公共点叫做切点。
定理:圆的切线垂直于过切点的半径。
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
分析:设????:????=????,????:直线????与圆????相切
要证????是????的充要条件,只需分别证明充
分性?????????和必要性?????????即可。
?
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
证明:设????:????=????,????:直线????与圆????相切
?
(1)充分性?????????:作????????⊥????于点????,则????????=????,若????=????,则点????在?????上.
在直线????上任取一点????(异于点????).连接????????.在?????????????????????中,????????>????????=????.所以,除点????外直线????上的点都在?????的外部,即直线????与圆????仅有一个公共点,所以直线????与圆????相切.
?
题型三:充要条件的证明
例3 已知?????的半径为????,圆心????到直线????的距离为????,求证:????=????是直线????与圆????相切的充要条件.
?
(2)必要性?????????:若直线????与圆????相切,不妨设切点为????,则????????⊥????,因此,????=????????=????.
?
证明:设????:????=????,????:直线????与圆????相切
?
由(1)(2)可得????=????是直线????与圆????相切的充要条件.
?
题型技法
关于充要条件命题的证明,一般分为充分性和必要性两个方面进行,其中由条件推出结论就是充分性,由结论推出条件就是必要性。
巩固训练
求证:关于????的方程????????????+????????+????=????有一个根为1的充要条件是????+????+????=????.
?
证明:????:????+????+????=????,????:关于????的方程????????????+????????+????=????有一个根为1
(1)充分性?????????:∵????+????+????=????,∴????=?
巩固训练
求证:关于????的方程????????????+????????+????=????有一个根为1的充要条件是????+????+????=????.
?
证明:????:????+????+????=????,????:关于????的方程????????????+????????+????=????有一个根为1
(2)必要性?????????:∵方程????????????+????????+????=????有一个根为1,∴????=????满足方程????????????+????????+????=????,即????+????+????=????.
由(1)(2)可得,关于????的方程????????????+????????+????=????有一个根为1的充要条件是????+????+????=????.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
