4 2 1等差数列的概念(第二课时) 课件(共18张PPT)-2020-2021学年高二数学人教A版选择性必修第二册
文档属性
| 名称 | 4 2 1等差数列的概念(第二课时) 课件(共18张PPT)-2020-2021学年高二数学人教A版选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 19:01:52 | ||
图片预览





文档简介
4.2.1等差数列的概念
(第二课时)
复习
1.等差数列的定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示。
符号表示:an - an-1=d(n≥2,n∈N*)
3.推到等差数列通项公式的方法:迭代法、累加法
4.由三个数a,A,b组成的等差数列可以看成是最简单的等差数列,这时A叫做a与b的等差中项。即
2.首项a1公差d,的等差数列{an}的通项公式为
求下列等差数列的通项公式
(1)9,18,27,36,45,54,63,72
(2)38,40,42,44,46,48.
(3)25,24,23,22,21.
(1)an=9n
(2)an=2n+36
(3)an=-n+26
思考:观察等差数列的通项公式,你认为它与我们熟悉的哪一类函数有关?
探究
新知
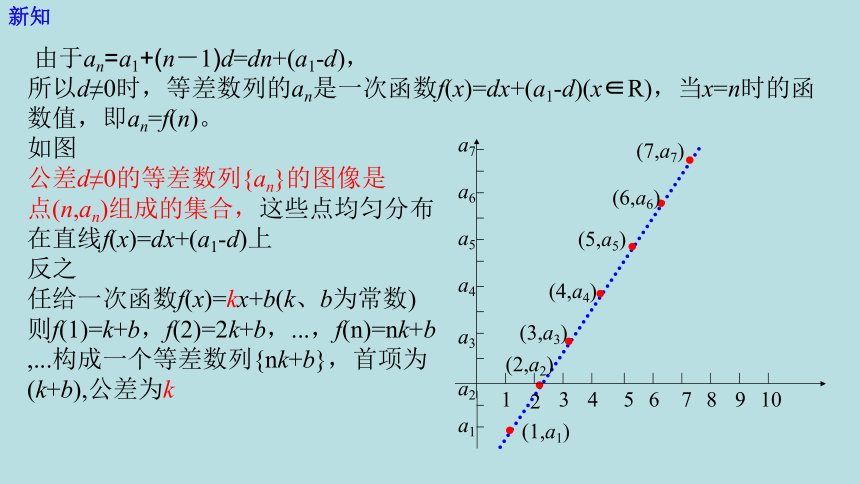
由于an=a1+(n-1)d=dn+(a1-d),
所以d≠0时,等差数列的an是一次函数f(x)=dx+(a1-d)(x∈R),当x=n时的函数值,即an=f(n)。
如图
公差d≠0的等差数列{an}的图像是
点(n,an)组成的集合,这些点均匀分布
在直线f(x)=dx+(a1-d)上
反之
任给一次函数f(x)=kx+b(k、b为常数)
则f(1)=k+b,f(2)=2k+b,...,f(n)=nk+b
,...构成一个等差数列{nk+b},首项为
(k+b),公差为k
●
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
10
(1,a1)
(2,a2)
(3,a3)
(4,a4)
(5,a5)
(6,a6)
(7,a7)
a1
a2
a3
a4
a5
a6
a7
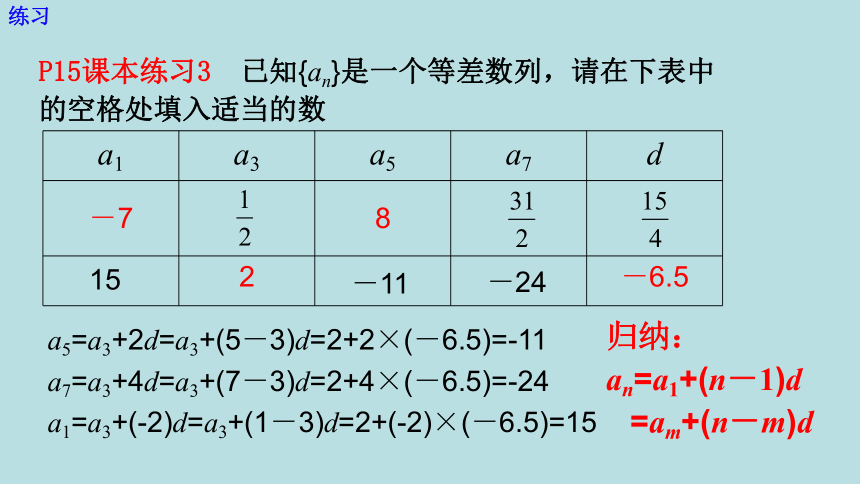
P15课本练习3 已知{an}是一个等差数列,请在下表中的空格处填入适当的数
{5940675A-B579-460E-94D1-54222C63F5DA}a1
a3
a5
a7
d
-7
8
2
-6.5
15
-11
-24
a5=a3+2d=a3+(5-3)d=2+2×(-6.5)=-11
a7=a3+4d=a3+(7-3)d=2+4×(-6.5)=-24
a1=a3+(-2)d=a3+(1-3)d=2+(-2)×(-6.5)=15
归纳:
an=a1+(n-1)d
=am+(n-m)d
练习
1.等差数列的定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示。
符号表示:an - an-1=d(n≥2,n∈N*)
2.首项a1公差d,的等差数列{an}的通项公式为
an=a1+(n-1)d=an=am+(n-m)d
新知
已知等差数列的任意两项可求公差
P15课本练习4 在7和21中插入3个数,使这5个数成等差数列
解:设等差数列{an}的首项为a1与公差为d
由题意可知a1=7,a5=21
∴
则a2=7+3.5=10.5
a3=7+2×3.5=14
a4=7+3×3.5=17.5
故在7和21中插入的3个数分别为10.5,14,17.5
∴a5=a1+4d=21 解得d=3.5
练习
例4.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:a1,a2,a3,a4,a5,...
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
例题
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
解:(1)设数列{bn}的公差为d′.
由题意可知,b1=a1,b5=a2,
于是b5-b1=a2-a1=8.
∵b5-b1=4d′,所以4d′ =8,所以d′ =2.
∴bn=2+(n-1)×2=2n
∴数列{bn}的通项公式是bn=2n.
例题
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:(2)①先求b29=?
②再求an
③令an=?,解出n
解:(2)由(1)可得b29=2×29=58
因为a1=2,d=8 所以an=8n-6
令8n-6=58 解得n=8
所以b29是数列{an}项,是第8项
例题
例4.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
a1,a2,a3,a4,a5,...,an ,...
b1,b5,b9 , ..., ....
b13 ,
b17 ,
b4n-3 ,
解:(2)数列{an}的各项依次是数列{bn}的第1,5,9,13....项,
这些下标构成一个首项为1,公差为4的等差数列{cn}
则cn =4n-3.
令4n-3=29,解得n=8.
所以,b29是数列{an}的第8项.
例题
已知等差数列{an}的通项公式为an=4n-3
则
(1)a1+a9= = a2+a8= =a3+a7= = 2a5= .
(2)a3+a15= = a5+a13= =a8+a10= = 2a9= .
34
34
34
17
34
66
66
66
33
66
猜想:等差数列{an},p,q,s,t,k∈N*,且p+q=s+t=2k,
则ap + aq = as + at= 2ak
探究
分析:只要根据等差数列的定义写出ap,aq,as,at,再利用已知条件即可得证。
证明:设数列{an}的公差为d,
则ap =a1+(p-1)d, aq =a1+(q-1)d,
as =a1+(s-1)d, at =a1+(t-1)d.
所以ap + aq =2a1+(p+q-2)d,
as + at =2a1+(s+t-2)d.
因为p+q=s+t,所以ap + aq = as + at.
例5:已知数列{an}是等差数列,p,q,s,t,∈N*,且p+q=s+t,则ap + aq = as + at
例题
18
练习:已知数列{an}是等差数列,
(1)若a2+a3+a10+a11=36,则a5+a8=________.
(2)a6+a9+a12+a15=20,则a1+a20= ;
(3)a3+a11=10,则a6+a7+a8= ;
10
15
练习
18
练习:已知数列{an}是等差数列,
(4)若a4+a7+a10=30,则a3-2a5=________.
(5)若a15=8,a60=20,则a75=________.
解:(4)法一:根据等差数列性质,可得a4+a10=2a7
a4+a7+a10=30=3a7 即a7 =10
∴a3-2a5=a3-(a3+a7)=-a7=-10
法二:根据题意,有(a1+3d)+(a1+6d)+(a1+9d)=30,
∴3a1+18d=3(a1+6d)=30 即a1+6d =10
∴a3-2a5=a1+3d-2(a1+4d)=-a1-6d=-(a1+6d)=-10
练习
18
练习:已知数列{an}是等差数列,
(4)若a4+a7+a10=30,则a3-2a5=________.
(5)若a15=8,a60=20,则a75=________.
练习
小结
1.当d≠0时,等差数列的an=a1+(n-1)d=dn+(a1-d)是一次函数f(x)=dx+(a1-d)(x∈R),当x=n时的函数值,即an=f(n)。
2.首项a1公差d,的等差数列{an}的通项公式为
an=a1+(n-1)d=an=am+(n-m)d
作业
P17课本练习 1、3、5
(第二课时)
复习
1.等差数列的定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示。
符号表示:an - an-1=d(n≥2,n∈N*)
3.推到等差数列通项公式的方法:迭代法、累加法
4.由三个数a,A,b组成的等差数列可以看成是最简单的等差数列,这时A叫做a与b的等差中项。即
2.首项a1公差d,的等差数列{an}的通项公式为
求下列等差数列的通项公式
(1)9,18,27,36,45,54,63,72
(2)38,40,42,44,46,48.
(3)25,24,23,22,21.
(1)an=9n
(2)an=2n+36
(3)an=-n+26
思考:观察等差数列的通项公式,你认为它与我们熟悉的哪一类函数有关?
探究
新知
由于an=a1+(n-1)d=dn+(a1-d),
所以d≠0时,等差数列的an是一次函数f(x)=dx+(a1-d)(x∈R),当x=n时的函数值,即an=f(n)。
如图
公差d≠0的等差数列{an}的图像是
点(n,an)组成的集合,这些点均匀分布
在直线f(x)=dx+(a1-d)上
反之
任给一次函数f(x)=kx+b(k、b为常数)
则f(1)=k+b,f(2)=2k+b,...,f(n)=nk+b
,...构成一个等差数列{nk+b},首项为
(k+b),公差为k
●
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
10
(1,a1)
(2,a2)
(3,a3)
(4,a4)
(5,a5)
(6,a6)
(7,a7)
a1
a2
a3
a4
a5
a6
a7
P15课本练习3 已知{an}是一个等差数列,请在下表中的空格处填入适当的数
{5940675A-B579-460E-94D1-54222C63F5DA}a1
a3
a5
a7
d
-7
8
2
-6.5
15
-11
-24
a5=a3+2d=a3+(5-3)d=2+2×(-6.5)=-11
a7=a3+4d=a3+(7-3)d=2+4×(-6.5)=-24
a1=a3+(-2)d=a3+(1-3)d=2+(-2)×(-6.5)=15
归纳:
an=a1+(n-1)d
=am+(n-m)d
练习
1.等差数列的定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示。
符号表示:an - an-1=d(n≥2,n∈N*)
2.首项a1公差d,的等差数列{an}的通项公式为
an=a1+(n-1)d=an=am+(n-m)d
新知
已知等差数列的任意两项可求公差
P15课本练习4 在7和21中插入3个数,使这5个数成等差数列
解:设等差数列{an}的首项为a1与公差为d
由题意可知a1=7,a5=21
∴
则a2=7+3.5=10.5
a3=7+2×3.5=14
a4=7+3×3.5=17.5
故在7和21中插入的3个数分别为10.5,14,17.5
∴a5=a1+4d=21 解得d=3.5
练习
例4.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:a1,a2,a3,a4,a5,...
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
例题
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
解:(1)设数列{bn}的公差为d′.
由题意可知,b1=a1,b5=a2,
于是b5-b1=a2-a1=8.
∵b5-b1=4d′,所以4d′ =8,所以d′ =2.
∴bn=2+(n-1)×2=2n
∴数列{bn}的通项公式是bn=2n.
例题
例2.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:(2)①先求b29=?
②再求an
③令an=?,解出n
解:(2)由(1)可得b29=2×29=58
因为a1=2,d=8 所以an=8n-6
令8n-6=58 解得n=8
所以b29是数列{an}项,是第8项
例题
例4.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2) b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
a1,? , ? ,? , a2,? ,? ,? ,a3,...
b1,b2 , b3 ,b4 , b5,b6 , b7 , b8 , b9 ,...
a1,a2,a3,a4,a5,...,an ,...
b1,b5,b9 , ..., ....
b13 ,
b17 ,
b4n-3 ,
解:(2)数列{an}的各项依次是数列{bn}的第1,5,9,13....项,
这些下标构成一个首项为1,公差为4的等差数列{cn}
则cn =4n-3.
令4n-3=29,解得n=8.
所以,b29是数列{an}的第8项.
例题
已知等差数列{an}的通项公式为an=4n-3
则
(1)a1+a9= = a2+a8= =a3+a7= = 2a5= .
(2)a3+a15= = a5+a13= =a8+a10= = 2a9= .
34
34
34
17
34
66
66
66
33
66
猜想:等差数列{an},p,q,s,t,k∈N*,且p+q=s+t=2k,
则ap + aq = as + at= 2ak
探究
分析:只要根据等差数列的定义写出ap,aq,as,at,再利用已知条件即可得证。
证明:设数列{an}的公差为d,
则ap =a1+(p-1)d, aq =a1+(q-1)d,
as =a1+(s-1)d, at =a1+(t-1)d.
所以ap + aq =2a1+(p+q-2)d,
as + at =2a1+(s+t-2)d.
因为p+q=s+t,所以ap + aq = as + at.
例5:已知数列{an}是等差数列,p,q,s,t,∈N*,且p+q=s+t,则ap + aq = as + at
例题
18
练习:已知数列{an}是等差数列,
(1)若a2+a3+a10+a11=36,则a5+a8=________.
(2)a6+a9+a12+a15=20,则a1+a20= ;
(3)a3+a11=10,则a6+a7+a8= ;
10
15
练习
18
练习:已知数列{an}是等差数列,
(4)若a4+a7+a10=30,则a3-2a5=________.
(5)若a15=8,a60=20,则a75=________.
解:(4)法一:根据等差数列性质,可得a4+a10=2a7
a4+a7+a10=30=3a7 即a7 =10
∴a3-2a5=a3-(a3+a7)=-a7=-10
法二:根据题意,有(a1+3d)+(a1+6d)+(a1+9d)=30,
∴3a1+18d=3(a1+6d)=30 即a1+6d =10
∴a3-2a5=a1+3d-2(a1+4d)=-a1-6d=-(a1+6d)=-10
练习
18
练习:已知数列{an}是等差数列,
(4)若a4+a7+a10=30,则a3-2a5=________.
(5)若a15=8,a60=20,则a75=________.
练习
小结
1.当d≠0时,等差数列的an=a1+(n-1)d=dn+(a1-d)是一次函数f(x)=dx+(a1-d)(x∈R),当x=n时的函数值,即an=f(n)。
2.首项a1公差d,的等差数列{an}的通项公式为
an=a1+(n-1)d=an=am+(n-m)d
作业
P17课本练习 1、3、5
