3 1函数的单调性(第一课时)课件(共35张PPT)——2021-2022学年高一上学期数学北师大版必修第一册
文档属性
| 名称 | 3 1函数的单调性(第一课时)课件(共35张PPT)——2021-2022学年高一上学期数学北师大版必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览






文档简介
3.1函数的单调性
第一课时
教学目标
01
02
会划分函数的单调区间,判断单调性
03
会用定义证明函数的单调性.
理解函数单调区间、单调性等概念.
1.理解函数单调区间、单调性等概念
2.会划分函数的单调区间,判断单调性
重点
难点
会用定义证明函数的单调性
环节一
创设情境
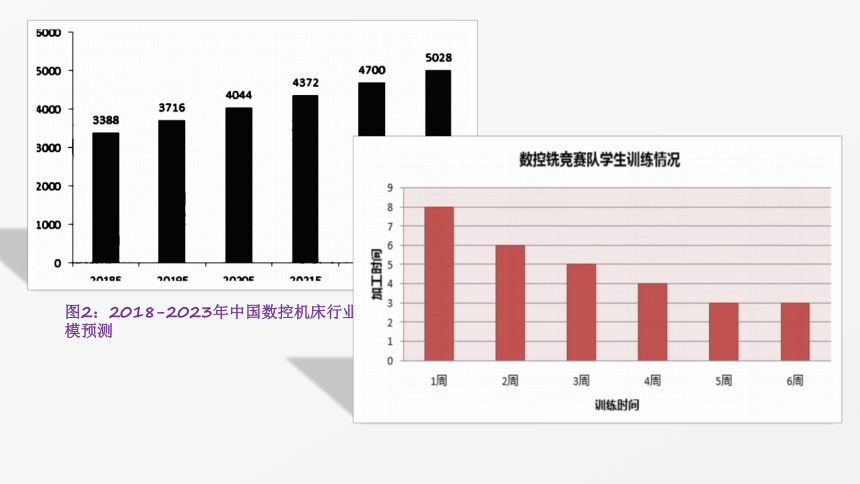
图2:2018-2023年中国数控机床行业市场规模预测
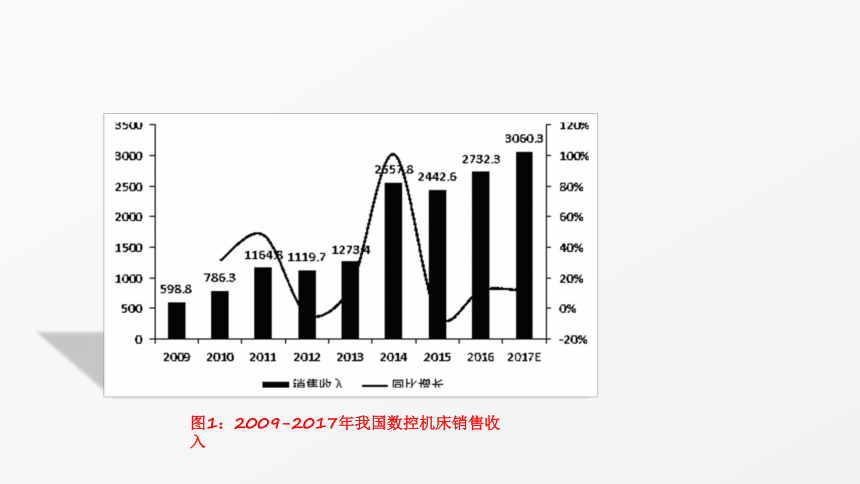
图1:2009-2017年我国数控机床销售收入
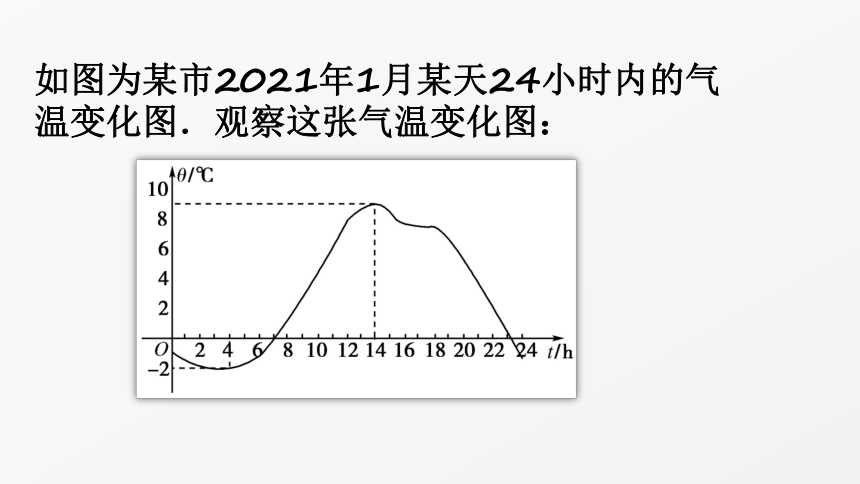
如图为某市2021年1月某天24小时内的气温变化图.观察这张气温变化图:
环节二
增减性概念
01
自然语言
单调性
对于自变量变化时,函数值是变大还是变小,是函数的重要性质,称为函数的单调性,同学们在初中对函数的这种性质就有了一定的认识,但是没有严格的定义
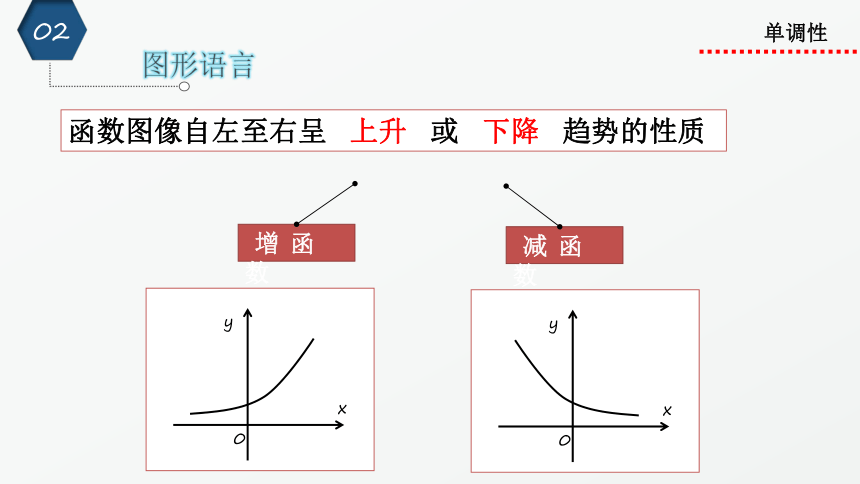
函数图像自左至右呈 上升 或 下降 趋势的性质
增 函 数
减 函 数
x
y
0
x
y
0
02
图形语言
单调性
03
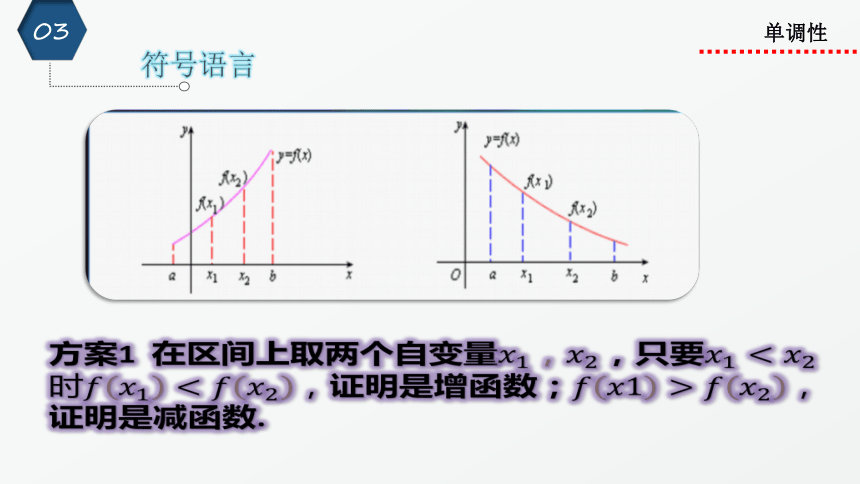
符号语言
单调性
方案1 在区间上取两个自变量????????,????????,只要????????????????????,证明是减函数.
?
03
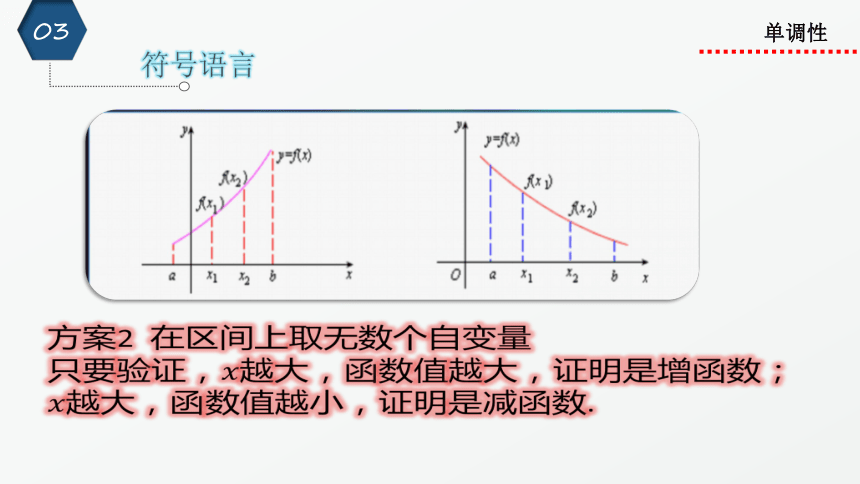
符号语言
单调性
方案2 在区间上取无数个自变量只要验证,????越大,函数值越大,证明是增函数;????越大,函数值越小,证明是减函数.
?
03
符号语言
单调性
方案3 区间上的任意两个自变量x1,x2,当x1f(x2),则为减函数;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
条件
结论
定义
增函数
设函数f(x)的定义域为I,定义域I内某个区间D上的任意两个自变量x1,x2
当x1f(x)在区间D上是
增函数
减函数
当x1f(x2)
f(x)在区间D上是
减函数
增函数与减函数的定义
(1)任意性,即x1,x2是在某一区间上的任意两个值,不能以特殊值代换;
(2)有大小,即确定的两个值x1,x2必须区分大小,一般令x1(3)同属一个单调区间.
x1,x2的三个特征解读
思考
1.定义中的“任意x1,x2∈D”能否改成“存在x1,x2∈D”?
不能
思考
2.函数y=????????在(-∞,0)上和(0,+∞)上都是减函数,能否说它在整个定义域上是减函数?
?
正确的写法是
减区间是?∞,
注意
①单调性是对定义域内某个区间而言的,离开了定义域和相应区间就谈不上单调性.
②有的函数在整个定义域内单调(如一次函数),有的函数只在定义域内的某些区间单调(如二次函数),有的函数根本没有单调区间(如常函数).
③函数在定义域内的两个区间A,B上都是增(或减)函数,一般不能认为函数在 ????∪????上是增(或减)函数.但有时候也可以。
?
函数的图像如下图所示,能否说:
函数在 ?
环节三
判断增减性
图像法
角度一
利用图像,可以直接观察出函数的增减变化情况
例1.下列函数中,在区间(0,+∞)上是减函数的是( )
A.y=-???????? B.y=x
C.y=x2 D.y=1-x
?
D 函数y=1-x在区间(0,+∞)上是减函数,其余函数在(0,+∞)上均为增函数,故选D.
初中常见函数的图像
一次
二次
反比例
高中常见函数的图像
指数
对数
三角函数
定义法
角度二
例2.定义法证明一次函数单调性
定义域为R,
任取????????,?????????∈????,设????????????????????????????????????=?????????????+?????(?????????????+????) = ?????????????+??????????????????????? =k?????????????????
因为????????所以当k>0时,k????????????????? 当k<0时,k?????????????????>????,即?????????????所以当k>0时,?????????在R上是增函数,
当k<0时, ?????????在R上是减函数
?
定义域
任取值
作差变形
判断符号
得出结论
定义法
角度二
判断并证明函数f(x)=?????????+1在(0,+∞)上的单调性
?
[解] 函数f(x)=-????????+1在(0,+∞)上是增函数.证明如下:
设x1,x2是(0,+∞)上的任意两个实数,且x1则f(x1)-f(x2) =?????????????+
环节四
求增减区间
图像法
角度一
2 4 6 8 10 12 14 16 18 20 22 24
10
8
6
4
2
-2
0
θ/?C
t/h
y=f(x),x∈[0,24]
函数在区间[4,14]上单调递增;
在区间[0,4]和[14,24]上单调递减.
例3
图像法
角度一
例4.函数y=f(x)的图象如图所示,其单调递增区间是( )
A.[-4,4] B.[-4,-3]∪[1,4]
C.[-3,1] D.[-3,4]
图像法
角度一
例5.画出函数y=-x2+2|x|+1的图象并写出函数的单调区间.
[解] y=-x2+2x+1,x≥0,-x2-2x+1,x<0,
函数的大致图象如图所示,
单调增区间为(-∞,-1],[0,1],单调减区间为(-1,0),(1,+∞).
【说明】也可以用【翻转法】快速做图(详见2.2.2函数表示法第二课时)
例6.求函数f(x)=-(x-3)????的单调区间.
?
分析
这种含绝对值的二次函数,只有用【分段函数法】画图,这在《2.2.2函数表示法第二课时》中介绍过。
[解] f=?????2+3????,????≥0????2?3????,????<0
作出该函数的图象,观察图象知递增区间为,递减区间为,.
?
定义法
角度二
例7.求函数f(x)=????
图像法和定义法对比
在求区间方面
1.图像法直观,定义法严谨;
2.使用定义法前,也可以用图像法,得到增减区间,再用定义法严格证明。当然,在小题中,能用图像法,就没必要再用定义法。所以,与其说定义法求区间,不如说是验证你前期的猜想。
3.如果图像画不出来,定义也不想使用,怎么办?将来会学导数法
课堂小结
1.核心要点
1.单调性和单调区间概念;
2.求区间、判断单调性、用定义证明
2.数学素养
1.通过单调区间、单调性等概念的学习,培养抽象概括素养.
2.通过用定义证明函数的单调性,培养逻辑推理素养.
谢谢观看
第一课时
教学目标
01
02
会划分函数的单调区间,判断单调性
03
会用定义证明函数的单调性.
理解函数单调区间、单调性等概念.
1.理解函数单调区间、单调性等概念
2.会划分函数的单调区间,判断单调性
重点
难点
会用定义证明函数的单调性
环节一
创设情境
图2:2018-2023年中国数控机床行业市场规模预测
图1:2009-2017年我国数控机床销售收入
如图为某市2021年1月某天24小时内的气温变化图.观察这张气温变化图:
环节二
增减性概念
01
自然语言
单调性
对于自变量变化时,函数值是变大还是变小,是函数的重要性质,称为函数的单调性,同学们在初中对函数的这种性质就有了一定的认识,但是没有严格的定义
函数图像自左至右呈 上升 或 下降 趋势的性质
增 函 数
减 函 数
x
y
0
x
y
0
02
图形语言
单调性
03
符号语言
单调性
方案1 在区间上取两个自变量????????,????????,只要????????????????????,证明是减函数.
?
03
符号语言
单调性
方案2 在区间上取无数个自变量只要验证,????越大,函数值越大,证明是增函数;????越大,函数值越小,证明是减函数.
?
03
符号语言
单调性
方案3 区间上的任意两个自变量x1,x2,当x1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
条件
结论
定义
增函数
设函数f(x)的定义域为I,定义域I内某个区间D上的任意两个自变量x1,x2
当x1
增函数
减函数
当x1
f(x)在区间D上是
减函数
增函数与减函数的定义
(1)任意性,即x1,x2是在某一区间上的任意两个值,不能以特殊值代换;
(2)有大小,即确定的两个值x1,x2必须区分大小,一般令x1
x1,x2的三个特征解读
思考
1.定义中的“任意x1,x2∈D”能否改成“存在x1,x2∈D”?
不能
思考
2.函数y=????????在(-∞,0)上和(0,+∞)上都是减函数,能否说它在整个定义域上是减函数?
?
正确的写法是
减区间是?∞,
注意
①单调性是对定义域内某个区间而言的,离开了定义域和相应区间就谈不上单调性.
②有的函数在整个定义域内单调(如一次函数),有的函数只在定义域内的某些区间单调(如二次函数),有的函数根本没有单调区间(如常函数).
③函数在定义域内的两个区间A,B上都是增(或减)函数,一般不能认为函数在 ????∪????上是增(或减)函数.但有时候也可以。
?
函数的图像如下图所示,能否说:
函数在 ?
环节三
判断增减性
图像法
角度一
利用图像,可以直接观察出函数的增减变化情况
例1.下列函数中,在区间(0,+∞)上是减函数的是( )
A.y=-???????? B.y=x
C.y=x2 D.y=1-x
?
D 函数y=1-x在区间(0,+∞)上是减函数,其余函数在(0,+∞)上均为增函数,故选D.
初中常见函数的图像
一次
二次
反比例
高中常见函数的图像
指数
对数
三角函数
定义法
角度二
例2.定义法证明一次函数单调性
定义域为R,
任取????????,?????????∈????,设????????????????????????????????????=?????????????+?????(?????????????+????) = ?????????????+??????????????????????? =k?????????????????
因为????????所以当k>0时,k????????????????? 当k<0时,k?????????????????>????,即?????????????所以当k>0时,?????????在R上是增函数,
当k<0时, ?????????在R上是减函数
?
定义域
任取值
作差变形
判断符号
得出结论
定义法
角度二
判断并证明函数f(x)=?????????+1在(0,+∞)上的单调性
?
[解] 函数f(x)=-????????+1在(0,+∞)上是增函数.证明如下:
设x1,x2是(0,+∞)上的任意两个实数,且x1
环节四
求增减区间
图像法
角度一
2 4 6 8 10 12 14 16 18 20 22 24
10
8
6
4
2
-2
0
θ/?C
t/h
y=f(x),x∈[0,24]
函数在区间[4,14]上单调递增;
在区间[0,4]和[14,24]上单调递减.
例3
图像法
角度一
例4.函数y=f(x)的图象如图所示,其单调递增区间是( )
A.[-4,4] B.[-4,-3]∪[1,4]
C.[-3,1] D.[-3,4]
图像法
角度一
例5.画出函数y=-x2+2|x|+1的图象并写出函数的单调区间.
[解] y=-x2+2x+1,x≥0,-x2-2x+1,x<0,
函数的大致图象如图所示,
单调增区间为(-∞,-1],[0,1],单调减区间为(-1,0),(1,+∞).
【说明】也可以用【翻转法】快速做图(详见2.2.2函数表示法第二课时)
例6.求函数f(x)=-(x-3)????的单调区间.
?
分析
这种含绝对值的二次函数,只有用【分段函数法】画图,这在《2.2.2函数表示法第二课时》中介绍过。
[解] f=?????2+3????,????≥0????2?3????,????<0
作出该函数的图象,观察图象知递增区间为,递减区间为,.
?
定义法
角度二
例7.求函数f(x)=????
图像法和定义法对比
在求区间方面
1.图像法直观,定义法严谨;
2.使用定义法前,也可以用图像法,得到增减区间,再用定义法严格证明。当然,在小题中,能用图像法,就没必要再用定义法。所以,与其说定义法求区间,不如说是验证你前期的猜想。
3.如果图像画不出来,定义也不想使用,怎么办?将来会学导数法
课堂小结
1.核心要点
1.单调性和单调区间概念;
2.求区间、判断单调性、用定义证明
2.数学素养
1.通过单调区间、单调性等概念的学习,培养抽象概括素养.
2.通过用定义证明函数的单调性,培养逻辑推理素养.
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
