1.2直线的方程(第3课时 直线的一般式)(备课件19张-)2021-2022学年高二数学同步备课系列(苏教版选择性必修第一册)
文档属性
| 名称 | 1.2直线的方程(第3课时 直线的一般式)(备课件19张-)2021-2022学年高二数学同步备课系列(苏教版选择性必修第一册) |  | |
| 格式 | pptx | ||
| 文件大小 | 508.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 19:20:05 | ||
图片预览






文档简介
1.2 直线的方程
第3课时 直线的一般式
学习目标
1.掌握直线的一般式方程
2.理解关于x,y的二元一次方程Ax+By+C=0(A,B不全为0)都表示直线
3.会进行直线方程的五种形式之间的转化
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
根据条件写出下列直线的方程:
复习引入
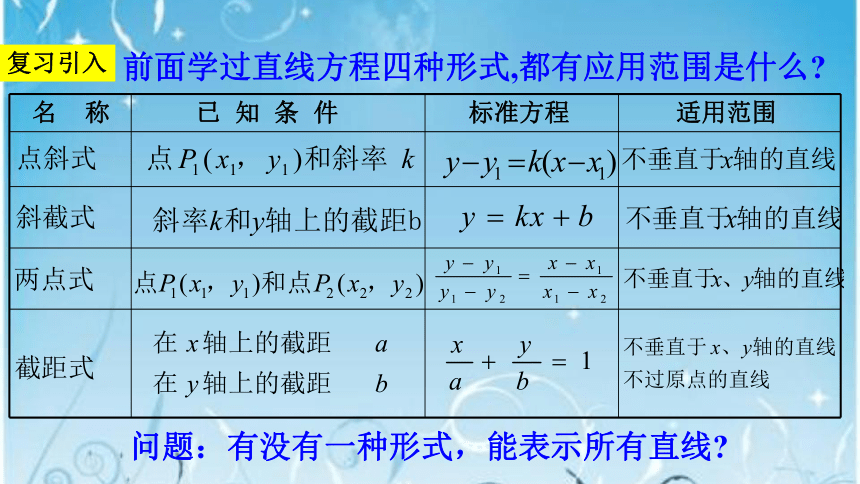
名 称
已 知 条 件
标准方程
适用范围
前面学过直线方程四种形式,都有应用范围是什么?
问题:有没有一种形式,能表示所有直线?
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
根据条件写出下列直线的方程:
x+2y+4=0
y-2=0
2x-y-3=0
x+y-1=0
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
x+2y+4=0
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
y-2=0
2x-y-3=0
x+y-1=0
根据条件写出下列直线的方程:
0x+y-2=0
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
x+2y+4=0
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
2x-y-3=0
x+y-1=0
根据条件写出下列直线的方程:
0x+y-2=0
直线的方程都可以化成形如Ax+By+C=0(A,B,C为常数)二元一次方程的形式
合作探究
Ax+By+C=0
都表示直线吗?
问题1:关于x和y的二元一次方程
小结:方程Ax+By+C=0,不一定代表直线,只有当A,B不同时为零时
Ax+By+C=0(A,B不全为零)
能表示所有直线吗?
问题2:关于x和y的二元一次方程
合作探究
Ax+By+C=0(A,B不全为零)
能表示所有直线吗?
问题2:关于x和y的二元一次方程
A≠0,B≠0
A=0,B≠0
A≠0,B=0
C=0
数学建构
一般地,方程
Ax+By+C=0(A,B不全为0)
叫做直线的一般式方程.
说明:
(1) 平面上的直线与二元一次方程是一一对应的;
(2)前面的四种形式都是一般方程的特殊情况.
数学应用
例1 求直线l:3x+5y-15=0的斜率以及它在 x轴、y轴上的截距,并作图.
例2
解析:
数学应用
解析:
例2
数学应用
x
y
O
解析:
例2
数学应用
直线的一般式与点斜式、斜截式、两点式、截距式的关系
根据条件选择恰当的
方程形式解决问题
x的系数一般不为分数和负数
课堂小结
达标测试
1.若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,则实数m的取值范围是 .
2.已知直线x-2y+2k=0 (k≠0)与两坐标轴围成的三角形面积
不大于1,则实数k的取值范围是 .
3.已知直线
(1)求直线l恒过的一个定点
(2)若当 时, 恒成立,求 的取值范围
1.若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,则实数m的取值范围是 .
解析 方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,
则2m2+m-3=0与m2-m=0不能同时成立.
故m的取值范围为(-∞,1)∪(1,+∞).
达标测试
2.已知直线x-2y+2k=0 (k≠0)与两坐标轴围成的三角形面积
不大于1,则实数k的取值范围是 .
解析 令x=0,则y=k,令y=0,则x=-2k,
所以直线与坐标轴所围成的三角形的面积是
所以-1≤k<0或0达标测试
3.已知直线
(1)求直线l恒过的一个定点
(2)若当 时, 恒成立,求 的取值范围
解析 (1)原方程可化为
所以直线l恒过定点(-2,1)
达标测试
谢谢!
第3课时 直线的一般式
学习目标
1.掌握直线的一般式方程
2.理解关于x,y的二元一次方程Ax+By+C=0(A,B不全为0)都表示直线
3.会进行直线方程的五种形式之间的转化
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
根据条件写出下列直线的方程:
复习引入
名 称
已 知 条 件
标准方程
适用范围
前面学过直线方程四种形式,都有应用范围是什么?
问题:有没有一种形式,能表示所有直线?
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
根据条件写出下列直线的方程:
x+2y+4=0
y-2=0
2x-y-3=0
x+y-1=0
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
x+2y+4=0
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
y-2=0
2x-y-3=0
x+y-1=0
根据条件写出下列直线的方程:
0x+y-2=0
复习引入
(1)斜率是- ,且经过点A(8,-6)的直线方程为____________.
x+2y+4=0
(2)经过点B(4,2),且平行于x轴的直线方程为_________.
(3)在x轴和y轴上的截距分别是 和-3的直线方程为_________.
(4)经过点P1(3,-2),P2(5,-4)的直线方程为____________.
2x-y-3=0
x+y-1=0
根据条件写出下列直线的方程:
0x+y-2=0
直线的方程都可以化成形如Ax+By+C=0(A,B,C为常数)二元一次方程的形式
合作探究
Ax+By+C=0
都表示直线吗?
问题1:关于x和y的二元一次方程
小结:方程Ax+By+C=0,不一定代表直线,只有当A,B不同时为零时
Ax+By+C=0(A,B不全为零)
能表示所有直线吗?
问题2:关于x和y的二元一次方程
合作探究
Ax+By+C=0(A,B不全为零)
能表示所有直线吗?
问题2:关于x和y的二元一次方程
A≠0,B≠0
A=0,B≠0
A≠0,B=0
C=0
数学建构
一般地,方程
Ax+By+C=0(A,B不全为0)
叫做直线的一般式方程.
说明:
(1) 平面上的直线与二元一次方程是一一对应的;
(2)前面的四种形式都是一般方程的特殊情况.
数学应用
例1 求直线l:3x+5y-15=0的斜率以及它在 x轴、y轴上的截距,并作图.
例2
解析:
数学应用
解析:
例2
数学应用
x
y
O
解析:
例2
数学应用
直线的一般式与点斜式、斜截式、两点式、截距式的关系
根据条件选择恰当的
方程形式解决问题
x的系数一般不为分数和负数
课堂小结
达标测试
1.若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,则实数m的取值范围是 .
2.已知直线x-2y+2k=0 (k≠0)与两坐标轴围成的三角形面积
不大于1,则实数k的取值范围是 .
3.已知直线
(1)求直线l恒过的一个定点
(2)若当 时, 恒成立,求 的取值范围
1.若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,则实数m的取值范围是 .
解析 方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,
则2m2+m-3=0与m2-m=0不能同时成立.
故m的取值范围为(-∞,1)∪(1,+∞).
达标测试
2.已知直线x-2y+2k=0 (k≠0)与两坐标轴围成的三角形面积
不大于1,则实数k的取值范围是 .
解析 令x=0,则y=k,令y=0,则x=-2k,
所以直线与坐标轴所围成的三角形的面积是
所以-1≤k<0或0
3.已知直线
(1)求直线l恒过的一个定点
(2)若当 时, 恒成立,求 的取值范围
解析 (1)原方程可化为
所以直线l恒过定点(-2,1)
达标测试
谢谢!
