1.3两条直线的平行与垂直(第1课时 两直线平行与垂直)(备课件)(19张PPT)-2021-2022学年高二数学同步备课系列(苏教版选择性必修第一册)
文档属性
| 名称 | 1.3两条直线的平行与垂直(第1课时 两直线平行与垂直)(备课件)(19张PPT)-2021-2022学年高二数学同步备课系列(苏教版选择性必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 327.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 19:14:33 | ||
图片预览





文档简介
1.3 两条直线的平行与垂直
学习目标
1.理解两条直线平行、垂直的判断条件.
2.能根据斜率判定两条直线平行和垂直,体会用代数方法研究几何问题的思想.
复习引入
问题1:平面内,两直线的位置关系有哪些?
问题2:初中时,如何判断平面内两直线平行?相交?垂直?
复习引入
问题1:平面内,两直线的位置关系有哪些?
问题2:初中时,如何判断平面内两直线平行?相交?垂直?
引入坐标系,我们就有了坐标,也就有了倾斜角和斜率,
倾斜角和斜率刻画了直线的倾斜程度,那么,能否用倾斜
角和斜率刻画两条直线的位置关系?
k =k
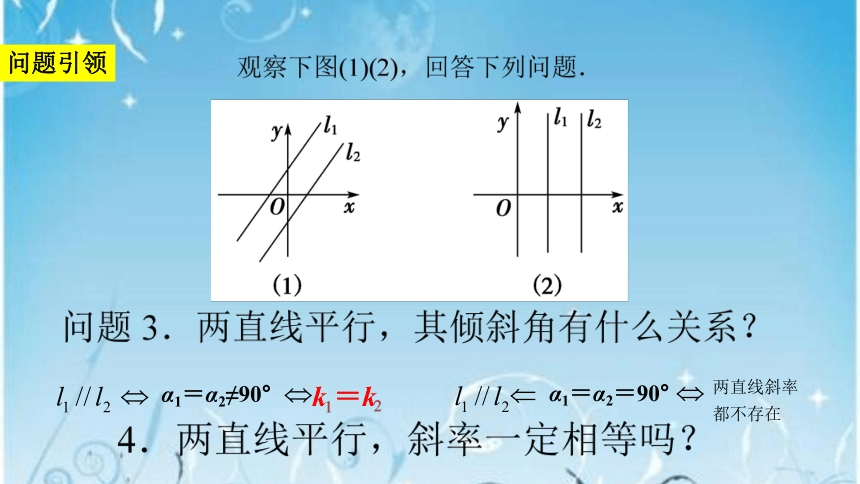
问题引领
α1=α2≠90°
α1=α2=90°
概念辨析
√
√
×
B
k1=k2且b1≠b2
l1∥l2
数学建构
结论:利用直线的斜截式判断两直线平行
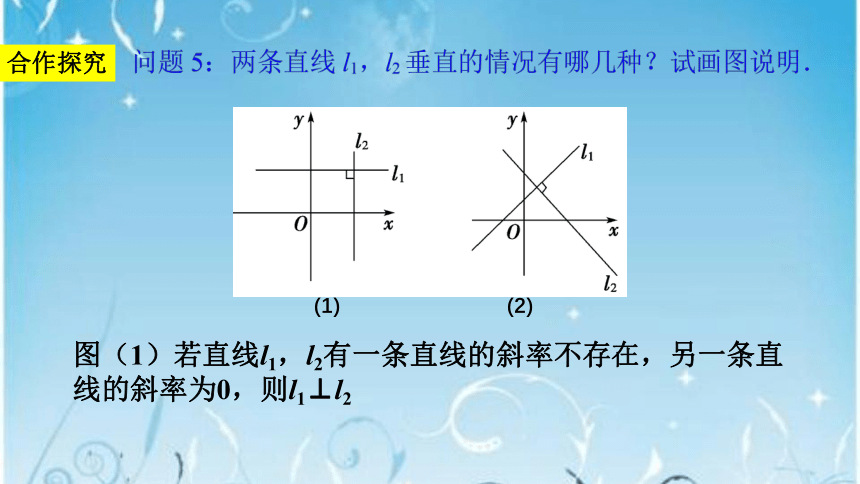
合作探究
(1)
(2)
图(1)若直线l1,l2有一条直线的斜率不存在,另一条直线的斜率为0,则l1⊥l2
数学建构
tan α2=tan(90°+α1)
α2=90°+α1
数学建构
1:设直线l1,l2(斜率存在)所对应的斜率分别为k1,k2,则
概念辨析
数学构建
l1⊥l2?k1k2=-1
我们有:
1:当直线l1和l2的方程为:l1:y=k1x+b1,l2:y=k2x+b2
结论:利用直线的斜截式判断两直线垂直
数学应用
数学应用
课堂小结
我们学到了什么?
l1∥l2 ? k1=k2且b1≠b2
l1⊥l2?k1k2=-1
利用直线l1和l2的斜截式方程:
l1:y=k1x+b1
l2:y=k2x+b2
1.判断两条直线平行与垂直方法:
2.判断方法的证明过程
等价关系的证明
数与形结合
归纳、猜想、证明
分类讨论
达标测试
2.求过点A(1,-4),且与直线2x+y+5=0平行的直线方程.
达标测试
达标测试
解:已知直线的斜率是-2,因为所求直线与已知直线平行,
所以它的斜率也是-2.
由点斜式得到所求直线的方程为:y+3=-2(x-2)
即为y=-2x+4
2.求过点A(1,-4),且与直线2x+y+5=0平行的直线方程.
谢谢!
学习目标
1.理解两条直线平行、垂直的判断条件.
2.能根据斜率判定两条直线平行和垂直,体会用代数方法研究几何问题的思想.
复习引入
问题1:平面内,两直线的位置关系有哪些?
问题2:初中时,如何判断平面内两直线平行?相交?垂直?
复习引入
问题1:平面内,两直线的位置关系有哪些?
问题2:初中时,如何判断平面内两直线平行?相交?垂直?
引入坐标系,我们就有了坐标,也就有了倾斜角和斜率,
倾斜角和斜率刻画了直线的倾斜程度,那么,能否用倾斜
角和斜率刻画两条直线的位置关系?
k =k
问题引领
α1=α2≠90°
α1=α2=90°
概念辨析
√
√
×
B
k1=k2且b1≠b2
l1∥l2
数学建构
结论:利用直线的斜截式判断两直线平行
合作探究
(1)
(2)
图(1)若直线l1,l2有一条直线的斜率不存在,另一条直线的斜率为0,则l1⊥l2
数学建构
tan α2=tan(90°+α1)
α2=90°+α1
数学建构
1:设直线l1,l2(斜率存在)所对应的斜率分别为k1,k2,则
概念辨析
数学构建
l1⊥l2?k1k2=-1
我们有:
1:当直线l1和l2的方程为:l1:y=k1x+b1,l2:y=k2x+b2
结论:利用直线的斜截式判断两直线垂直
数学应用
数学应用
课堂小结
我们学到了什么?
l1∥l2 ? k1=k2且b1≠b2
l1⊥l2?k1k2=-1
利用直线l1和l2的斜截式方程:
l1:y=k1x+b1
l2:y=k2x+b2
1.判断两条直线平行与垂直方法:
2.判断方法的证明过程
等价关系的证明
数与形结合
归纳、猜想、证明
分类讨论
达标测试
2.求过点A(1,-4),且与直线2x+y+5=0平行的直线方程.
达标测试
达标测试
解:已知直线的斜率是-2,因为所求直线与已知直线平行,
所以它的斜率也是-2.
由点斜式得到所求直线的方程为:y+3=-2(x-2)
即为y=-2x+4
2.求过点A(1,-4),且与直线2x+y+5=0平行的直线方程.
谢谢!
