三年级下册数学教案 7.5 整理与提高 数学广场(谁围出的面积更大) 沪教版
文档属性
| 名称 | 三年级下册数学教案 7.5 整理与提高 数学广场(谁围出的面积更大) 沪教版 |  | |
| 格式 | doc | ||
| 文件大小 | 54.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 11:49:01 | ||
图片预览


文档简介
谁围出的面积最大
教学目标:
知识与技能:知道并理解长方形周长相等时,长宽与面积之间的关系”。
过程与方法:通过动手操作围出图形,探究“长方形周长相等时,长宽与面积之间的关系”。
情感、态度、价值观:通过动手操作围出图形,发现规律,得出结论。感受数学的魅力,发展对数学的兴趣,获得成功的体验。
教学重难点:长方形周长相等时,长、宽与面积之间的关系
一、创设情境,提出问题
师:今天老师要给大家介绍一位非常了不起的人物——瑞士大数学家欧拉。
欧拉小时候就特别爱思考。有一次,他的父亲准备建一个新羊圈。
师:他准备在一块足够大的、空旷的土地上围一块长40米,宽15米的长方形的羊圈。这个长方形的面积是多少?周长是多少?(学生计算)
生:面积是600平方米,周长是110米。
师:周长是110米,可是父亲在准备动工时发现栅栏只有100米长,少了!父亲很为难:因为他既不想增加栅栏,又想使羊圈的面积足够大,那该怎么办呢?
(学生陷入思考)
师:谁能用自己的话说说对这道题的理解吗?
生:就是用100米长的栅栏,围成一个尽量大的羊圈。
生:其实就是周长固定,面积尽量大。
生:……
师:你们都说得很好!其实就是要解决周长一定,通过改变长方形的长和宽,使面积尽可能大的问题。
师:聪明的欧拉很快就帮父亲解决了难题。你想知道欧拉是怎么做的吗?这节课我们就学习“谁围出的面积最大”。(板书)
师:要解决问题就要找到解决问题的方法,周长是100的长方形数字大了,我们先换个简单一点的问题研究一下好吗?
二、动手操作、记录并反馈
(出示)用一根20根1cm厘米长的小棒围一个长方形(包括正方形),看谁围的图形面积最大?
思考:你准备怎样解决这个问题?你有什么问题或想法吗?
设想:1、20根火柴可以围成几个长方形?
2、长方形的长宽会是多少?
3、通过什么方式去比较谁的面积大?记录?看图?(这里老师给出方法:用记录表格的方法)
4、面积最大跟什么有关?
5、长和宽成何种关系时,图形面积最大?
小结:(1)、先用20根火柴围出各种形状的长方形。
(2)、再分别算算它们的面积,比一比谁的面积最大。
师:请大家用手中的棉签代替小棒动手围一围,在表一中记下每次探究的结果。
周长(cm) 长(cm) 宽(cm) 面积()
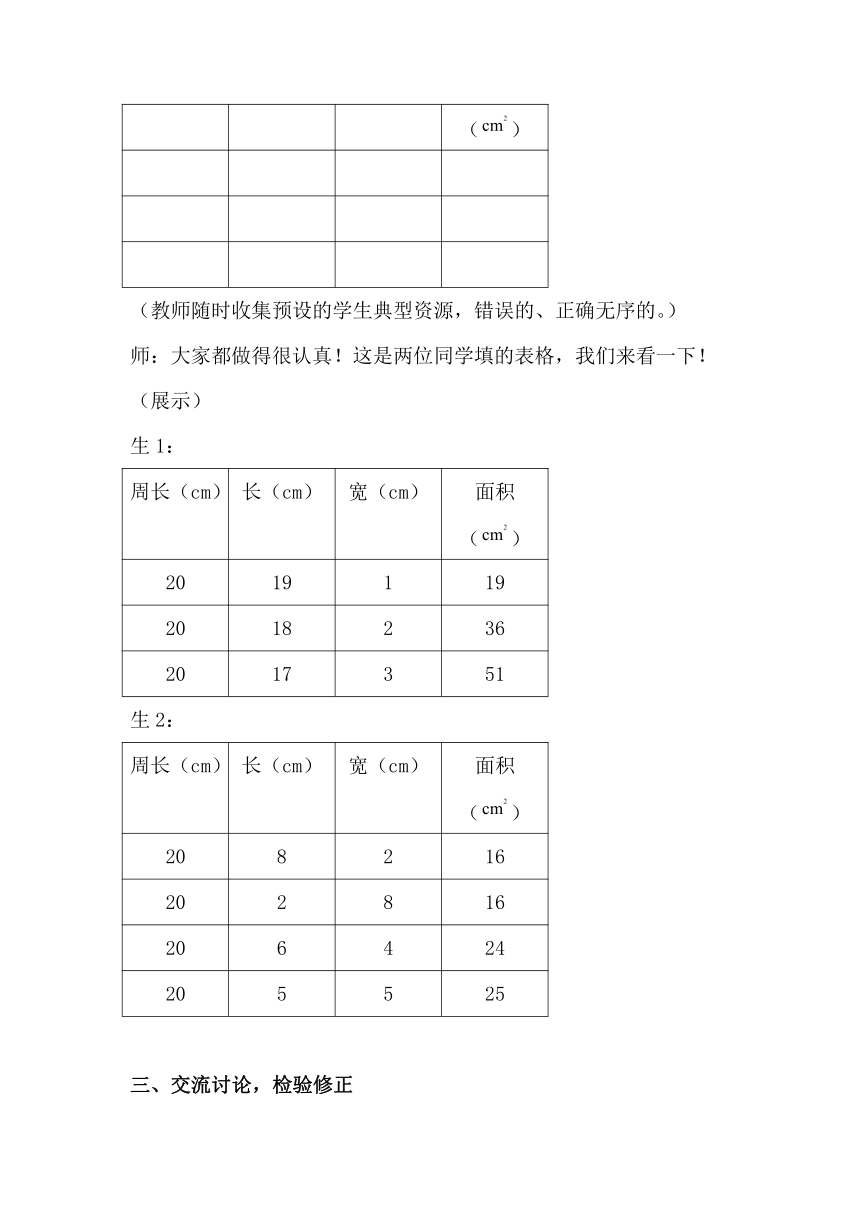
(教师随时收集预设的学生典型资源,错误的、正确无序的。)
师:大家都做得很认真!这是两位同学填的表格,我们来看一下!
(展示)
生1:
周长(cm) 长(cm) 宽(cm) 面积()
20 19 1 19
20 18 2 36
20 17 3 51
生2:
周长(cm) 长(cm) 宽(cm) 面积()
20 8 2 16
20 2 8 16
20 6 4 24
20 5 5 25
三、交流讨论,检验修正
师:同学们,看了这两位同学的表格,你有什么发现,你有什么想说的吗?
生:生1的表格是错的,周长是20厘米,“长+宽”应该是10厘米,而不是20厘米。
师:同学们,题目中周长是20厘米,这个20是长和宽的和吗?
生:不是。
师:那么“长+宽”和周长有什么关系呢?
生:“长+宽”是周长的一半。
师:非常好,这里我们就解决了问题2。板书:“长+宽”是周长的一半
那么生2的表格你们觉得怎么样呢?请大家就这张表格展开讨论,谈谈你认为填写表格时需要注意些什么?
(学生讨论)
生:我觉得他的填写过程有点乱。
生:长方形的长应该大于宽,所以表格第三行(长2、宽8)不对,应该倒一倒!
生:而且表格的第一种情况和第二种其实是一种情况,重复了!
生:他的表格还没有填写完整。
师:你们观察得真仔细!那你们觉得填表格时要注意些什么?
生:我觉得要有顺序。
生:要注意美观。
生:不能遗漏。
生:也不能重复!
师:你们回答得真好!我们在填表时一定要仔细认真,做到有序、不重复、不遗漏。
师:谁来向大家展示一下你的表格呢?
(生齐举手!)
(展示)
周长(cm) 长(cm) 宽(cm) 面积()
20 9 1 9
20 8 2 16
20 7 3 21
20 6 4 24
20 5 5 25
师: 现在我们来看是否可以解决问题1,20根小棒可以围成几个长方形?
四、得出结论,表达陈述
师:从表格中,你发现了什么?是否可以解决剩下的问题?
生:我发现面积越来越大了。
师:是啊,面积越来越大了!为什么面积会越来越大呢?
生:长越来越小了,宽越来越大了。
生:长和宽的差距越来越小,面积就越来越大。
师:什么时候面积最大呢?
生:当能围成正方形时,面积最大。
师:谁来回答最后两个问题?
初步得出结论:周长一定时,长方形长与宽相差越小(大),面积越大(小);围成的正方形面积最大。
五、质疑结论并验证
师:这个结论是否同样适用于其它周长一定的长方形呢?
(出示)分别用16、26厘米长的铁丝围成一个长方形,有多少种围法?怎样围面积最大?
男生女生分别完成表格,然后交流:
生:16厘米长铁丝:当长是4厘米,宽4厘米时,面积最大是16平方厘米。
26厘米长铁丝:当长是7厘米,宽6厘米时,面积最大是42平方厘米。
师:大家同意他的结果吗?
生:同意!
完成填空小结:
这些周长相等的长方形中,
长方形的长和宽的长度相差越大,面积就越( )。
长方形的长和宽的长度相差越小,面积就越( )。
当围成的长方形长与宽相等成为( )时,面积( )。
板书:周长一定时,长方形长与宽相差越小(大),面积越大(小);围成的正方形面积最大。
六、回顾欧拉问题
师:现在你知道欧拉的解决办法了吗?100米的栅栏怎么围可以围出最大的面积?
生:100米可以围出一个正方形,面积是最大的。
师:面积是多少呢?
生:周长是100米,正方形的边长就是25厘米,面积是625平方厘米。
师:同学们,你们都学得很认真。相信你们一定掌握了今天的知识!
七、联系生活,解决问题
师:你们知道吗围最大的面积在生活中有很大的用处!
1、小区想围出一个长方形的临时停车场,用一根长40米的绳子,围成的面积最大是( )平方米。
(1)、400 (2)、100 (3)、200
2、公园管理员叔叔要用18根一米长的铁栏杆来围一个最大的长方形花坛(长和宽都是整米数),它的长和宽各是( )米。
(1)、 3和6 (2)、 7和2 (3)、 4和5
师:围最大的面积不仅可以解决很多生活中的问题,还可以解决很多数学问题。
3、两个自然数的和是60,你认为这两个自然数的积最大是( )
4、两个自然数的和是41,你认为这两个自然数的积最大是( )
八、总结
教学目标:
知识与技能:知道并理解长方形周长相等时,长宽与面积之间的关系”。
过程与方法:通过动手操作围出图形,探究“长方形周长相等时,长宽与面积之间的关系”。
情感、态度、价值观:通过动手操作围出图形,发现规律,得出结论。感受数学的魅力,发展对数学的兴趣,获得成功的体验。
教学重难点:长方形周长相等时,长、宽与面积之间的关系
一、创设情境,提出问题
师:今天老师要给大家介绍一位非常了不起的人物——瑞士大数学家欧拉。
欧拉小时候就特别爱思考。有一次,他的父亲准备建一个新羊圈。
师:他准备在一块足够大的、空旷的土地上围一块长40米,宽15米的长方形的羊圈。这个长方形的面积是多少?周长是多少?(学生计算)
生:面积是600平方米,周长是110米。
师:周长是110米,可是父亲在准备动工时发现栅栏只有100米长,少了!父亲很为难:因为他既不想增加栅栏,又想使羊圈的面积足够大,那该怎么办呢?
(学生陷入思考)
师:谁能用自己的话说说对这道题的理解吗?
生:就是用100米长的栅栏,围成一个尽量大的羊圈。
生:其实就是周长固定,面积尽量大。
生:……
师:你们都说得很好!其实就是要解决周长一定,通过改变长方形的长和宽,使面积尽可能大的问题。
师:聪明的欧拉很快就帮父亲解决了难题。你想知道欧拉是怎么做的吗?这节课我们就学习“谁围出的面积最大”。(板书)
师:要解决问题就要找到解决问题的方法,周长是100的长方形数字大了,我们先换个简单一点的问题研究一下好吗?
二、动手操作、记录并反馈
(出示)用一根20根1cm厘米长的小棒围一个长方形(包括正方形),看谁围的图形面积最大?
思考:你准备怎样解决这个问题?你有什么问题或想法吗?
设想:1、20根火柴可以围成几个长方形?
2、长方形的长宽会是多少?
3、通过什么方式去比较谁的面积大?记录?看图?(这里老师给出方法:用记录表格的方法)
4、面积最大跟什么有关?
5、长和宽成何种关系时,图形面积最大?
小结:(1)、先用20根火柴围出各种形状的长方形。
(2)、再分别算算它们的面积,比一比谁的面积最大。
师:请大家用手中的棉签代替小棒动手围一围,在表一中记下每次探究的结果。
周长(cm) 长(cm) 宽(cm) 面积()
(教师随时收集预设的学生典型资源,错误的、正确无序的。)
师:大家都做得很认真!这是两位同学填的表格,我们来看一下!
(展示)
生1:
周长(cm) 长(cm) 宽(cm) 面积()
20 19 1 19
20 18 2 36
20 17 3 51
生2:
周长(cm) 长(cm) 宽(cm) 面积()
20 8 2 16
20 2 8 16
20 6 4 24
20 5 5 25
三、交流讨论,检验修正
师:同学们,看了这两位同学的表格,你有什么发现,你有什么想说的吗?
生:生1的表格是错的,周长是20厘米,“长+宽”应该是10厘米,而不是20厘米。
师:同学们,题目中周长是20厘米,这个20是长和宽的和吗?
生:不是。
师:那么“长+宽”和周长有什么关系呢?
生:“长+宽”是周长的一半。
师:非常好,这里我们就解决了问题2。板书:“长+宽”是周长的一半
那么生2的表格你们觉得怎么样呢?请大家就这张表格展开讨论,谈谈你认为填写表格时需要注意些什么?
(学生讨论)
生:我觉得他的填写过程有点乱。
生:长方形的长应该大于宽,所以表格第三行(长2、宽8)不对,应该倒一倒!
生:而且表格的第一种情况和第二种其实是一种情况,重复了!
生:他的表格还没有填写完整。
师:你们观察得真仔细!那你们觉得填表格时要注意些什么?
生:我觉得要有顺序。
生:要注意美观。
生:不能遗漏。
生:也不能重复!
师:你们回答得真好!我们在填表时一定要仔细认真,做到有序、不重复、不遗漏。
师:谁来向大家展示一下你的表格呢?
(生齐举手!)
(展示)
周长(cm) 长(cm) 宽(cm) 面积()
20 9 1 9
20 8 2 16
20 7 3 21
20 6 4 24
20 5 5 25
师: 现在我们来看是否可以解决问题1,20根小棒可以围成几个长方形?
四、得出结论,表达陈述
师:从表格中,你发现了什么?是否可以解决剩下的问题?
生:我发现面积越来越大了。
师:是啊,面积越来越大了!为什么面积会越来越大呢?
生:长越来越小了,宽越来越大了。
生:长和宽的差距越来越小,面积就越来越大。
师:什么时候面积最大呢?
生:当能围成正方形时,面积最大。
师:谁来回答最后两个问题?
初步得出结论:周长一定时,长方形长与宽相差越小(大),面积越大(小);围成的正方形面积最大。
五、质疑结论并验证
师:这个结论是否同样适用于其它周长一定的长方形呢?
(出示)分别用16、26厘米长的铁丝围成一个长方形,有多少种围法?怎样围面积最大?
男生女生分别完成表格,然后交流:
生:16厘米长铁丝:当长是4厘米,宽4厘米时,面积最大是16平方厘米。
26厘米长铁丝:当长是7厘米,宽6厘米时,面积最大是42平方厘米。
师:大家同意他的结果吗?
生:同意!
完成填空小结:
这些周长相等的长方形中,
长方形的长和宽的长度相差越大,面积就越( )。
长方形的长和宽的长度相差越小,面积就越( )。
当围成的长方形长与宽相等成为( )时,面积( )。
板书:周长一定时,长方形长与宽相差越小(大),面积越大(小);围成的正方形面积最大。
六、回顾欧拉问题
师:现在你知道欧拉的解决办法了吗?100米的栅栏怎么围可以围出最大的面积?
生:100米可以围出一个正方形,面积是最大的。
师:面积是多少呢?
生:周长是100米,正方形的边长就是25厘米,面积是625平方厘米。
师:同学们,你们都学得很认真。相信你们一定掌握了今天的知识!
七、联系生活,解决问题
师:你们知道吗围最大的面积在生活中有很大的用处!
1、小区想围出一个长方形的临时停车场,用一根长40米的绳子,围成的面积最大是( )平方米。
(1)、400 (2)、100 (3)、200
2、公园管理员叔叔要用18根一米长的铁栏杆来围一个最大的长方形花坛(长和宽都是整米数),它的长和宽各是( )米。
(1)、 3和6 (2)、 7和2 (3)、 4和5
师:围最大的面积不仅可以解决很多生活中的问题,还可以解决很多数学问题。
3、两个自然数的和是60,你认为这两个自然数的积最大是( )
4、两个自然数的和是41,你认为这两个自然数的积最大是( )
八、总结
