2021—2022学年人教版数学九年级上册:23.2.3 关于原点对称的点的坐标自学自测 word版,含答案
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册:23.2.3 关于原点对称的点的坐标自学自测 word版,含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 265.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 13:26:33 | ||
图片预览


文档简介
23.2.3
关于原点对称的点的坐标自学自测
一、选择题
1.已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是
(
)
2.
在平面直角坐标系中,点P(-1,m2+1)关于原点对称的点在
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.如图,点关于原点对称后落在直线上点处,则的值为(
)
A.
B.
C.
D.
4.若点P(-a,a-3)关于原点对称的点在第三象限内,则a满足
(
)
A.a>3
B.0C.a<0
D.a<0或a>3
5.已知点与点关于原点对称,则的值为( )
A.5
B.-5
C.1
D.-1
6.点A(-3,2)关于原点的对称点是B,点B关于x轴的对称点是C,则点C的坐标是
(
)
A.(3,2)
B.(-3,2)
C.(3,-2)
D.(-2,3)
7.
点A(-3,2)关于原点对称的点是B,点B关于y轴对称的点是C,则点C的坐标是(
)
A.(3,-2)
B.(3,2)
C.(-3,-2)
D.(-3,2)
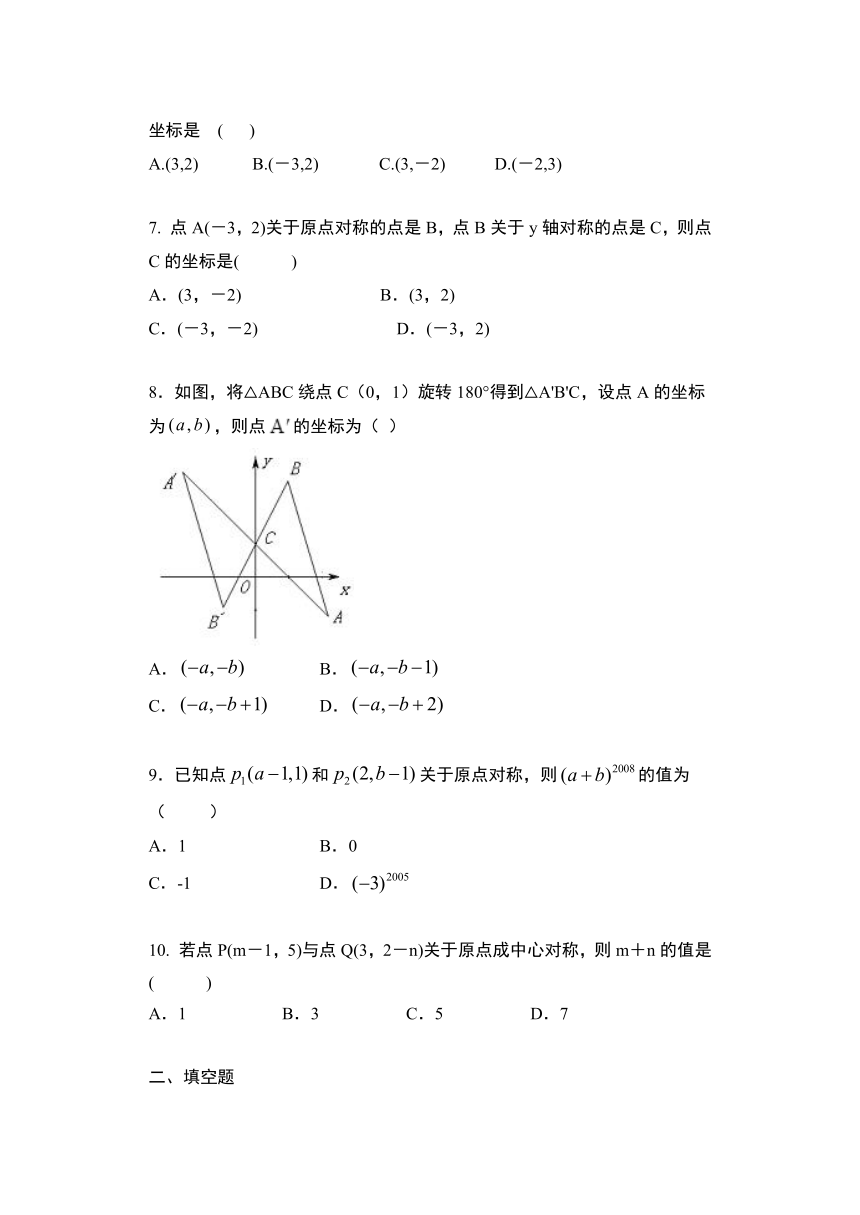
8.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为,则点的坐标为(
)
A.
B.
C.
D.
9.已知点和关于原点对称,则的值为(
)
A.1
B.0
C.-1
D.
10.
若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是(
)
A.1
B.3
C.5
D.7
二、填空题
11.
已知点P关于x轴的对称点P1的坐标是(5,8),则点P关于原点的对称点P2的坐标是__
__.
12.
若点P(2a+3b,-2)关于原点的对称点为Q(3,a-2b),则(3a+b)2
020= .
13.二次函数y=x2-2x-3的图象关于原点O(0,0)对称的图象的解析式是_________.
14.△ABC三个顶点的坐标依次为A(1,-1),B(4,1)和C(2,2),将△ABC绕坐标原点旋转180°,旋转后所得三角形各顶点的坐标依次为
.?
15.已知点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,则(x+y)y的值是__
__.
16.已知点P(3+2a,2a+1)与点P'关于原点成中心对称.若点P'在第二象限,且a为整数,则关于x的分式方程=3的解是
.?
三、解答题
17.如图,AB∥CD∥x轴,且AB=CD=3,已知点A(-1,1),C(1,-1).
(1)写出点B,D的坐标.
(2)你发现点A,B,C,D之间有何关系?
18.
如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.
(1)请按下列要求画图:
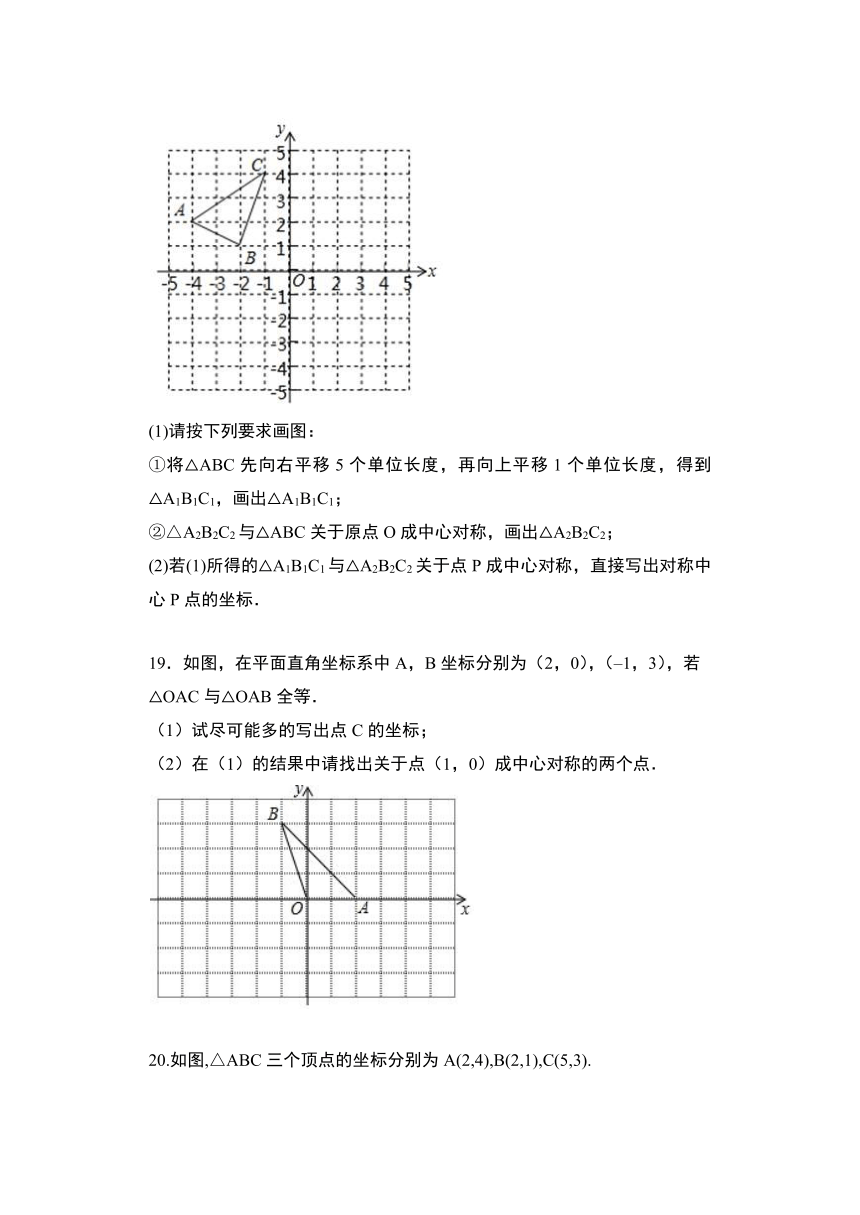
①将△ABC先向右平移5个单位长度,再向上平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2关于点P成中心对称,直接写出对称中心P点的坐标.
19.如图,在平面直角坐标系中A,B坐标分别为(2,0),(–1,3),若△OAC与△OAB全等.
(1)试尽可能多的写出点C的坐标;
(2)在(1)的结果中请找出关于点(1,0)成中心对称的两个点.
20.如图,△ABC三个顶点的坐标分别为A(2,4),B(2,1),C(5,3).
(1)请在网格中,画出△ABC关于原点对称的△A1B1C1;
(2)请在网格中,过点A画一条直线AD,将△ABC分成面积相等的两部分,与x轴相交于点D,并写出点D的坐标.
21.如图所示,在平面直角坐标系中,△PQR是由△ABC经过某种变换后得到的图形.
⑴仔细观察点A和点P,点B和点Q,点C和点R的坐标之间的关系,在这种变换下分别写出这六个点的坐标,从中你发现什么特征?请你用文字语言将你发现的特征表达出来;
⑵若△ABC内有一点M(2a+5,-1-3b)经过变换后,在△PRQ内的坐标为(-3,-2),根据你发现的特征,求关于x的方程2-ax=bx-3的解.
22.如图,已知点A(2,3)和直线y=x.
(1)分别写出点A关于直线y=x的对称点B和关于原点的对称点C的坐标;
(2)若D是点B关于原点的对称点,判断四边形ABCD的形状,并说明理由.
23.阅读下列材料并完成题目:
类似于平移变换是在原有横、纵坐标上加减一个数,在平面直角坐标系xOy中,点P(x,y)经过变换φ得到P′(x′,y′),把这种变换记作φ(x,y)=(x′,y′),其中(a,b为常数),例如:当a=1,且b=1时,则φ(﹣2,3)=(1,﹣5).
(1)①当a=2,且b=1时,φ(﹣2,1)=
.
②若φ(3,1)=(﹣3,﹣3),则a=
,b=
.
(2)点P(2,1)经过变换φ得到点P′(x′,y′),若点P′与点P关于原点对称,求a和b的值.
(3)对任意横、纵坐标满足二元一次方程2x﹣y=0的点P(x,y),点P经过变换φ得到点P′(x′,y′),若点P与点P′重合,求a和b的值.
答案
一、选择题
1.
C
2.
D
3.
B
4.
D
5.
C
6.
A
7.
C
8.
D
9.
A
10.
C
二、填空题
11.
(-5,8)
12.
1
13.
Y=-x2-2x+3(写成顶点式也对)
14.
(-1,1) , (-4,-1) , (-2,-2)
15.
1
16.
x=-2
三、解答题
17.
解:(1)点B的坐标为(2,1),点D的坐标为(-2,-1).
(2)点A与点C关于原点对称,点B与点D关于原点对称.
18.
(1)
解:①△A1B1C1如图所示.②△A2B2C2如图所示.
(2)
解:△A1B1C1与△A2B2C2关于点P成中心对称,如图,点P的坐标是(2.5,0.5).
19.
(1)(3,3)或(–1,–3)或(3,–3);(2)(–1,–3)、(3,3)
20.解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,直线AD即为所求;点D的坐标为(5,0).
21.
⑴A(4,3),B(3,1),C(1,2),P(-4,-3),Q(-3,-1),R(-1,-2),△ABC所在平面上各点与△PQR所在平面的对应点关于原点对称;⑵x=-
22.
解:(1)B(3,2),C(-2,-3).
(2)四边形ABCD是矩形.
理由:∵点B(3,2)关于原点的对称点为D(-3,-2).又∵点B和点D关于原点对称,∴BO=DO.同理AO=CO,∴四边形ABCD是平行四边形.∵点A关于直线y=x的对称点为B,点A关于原点的对称点为C,∴AC=BD,∴四边形ABCD是矩形.
23.
(1)①(﹣3,﹣5);②﹣1,0;(2);(3),.
试卷第8页,总8页
关于原点对称的点的坐标自学自测
一、选择题
1.已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是
(
)
2.
在平面直角坐标系中,点P(-1,m2+1)关于原点对称的点在
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.如图,点关于原点对称后落在直线上点处,则的值为(
)
A.
B.
C.
D.
4.若点P(-a,a-3)关于原点对称的点在第三象限内,则a满足
(
)
A.a>3
B.0
D.a<0或a>3
5.已知点与点关于原点对称,则的值为( )
A.5
B.-5
C.1
D.-1
6.点A(-3,2)关于原点的对称点是B,点B关于x轴的对称点是C,则点C的坐标是
(
)
A.(3,2)
B.(-3,2)
C.(3,-2)
D.(-2,3)
7.
点A(-3,2)关于原点对称的点是B,点B关于y轴对称的点是C,则点C的坐标是(
)
A.(3,-2)
B.(3,2)
C.(-3,-2)
D.(-3,2)
8.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为,则点的坐标为(
)
A.
B.
C.
D.
9.已知点和关于原点对称,则的值为(
)
A.1
B.0
C.-1
D.
10.
若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是(
)
A.1
B.3
C.5
D.7
二、填空题
11.
已知点P关于x轴的对称点P1的坐标是(5,8),则点P关于原点的对称点P2的坐标是__
__.
12.
若点P(2a+3b,-2)关于原点的对称点为Q(3,a-2b),则(3a+b)2
020= .
13.二次函数y=x2-2x-3的图象关于原点O(0,0)对称的图象的解析式是_________.
14.△ABC三个顶点的坐标依次为A(1,-1),B(4,1)和C(2,2),将△ABC绕坐标原点旋转180°,旋转后所得三角形各顶点的坐标依次为
.?
15.已知点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,则(x+y)y的值是__
__.
16.已知点P(3+2a,2a+1)与点P'关于原点成中心对称.若点P'在第二象限,且a为整数,则关于x的分式方程=3的解是
.?
三、解答题
17.如图,AB∥CD∥x轴,且AB=CD=3,已知点A(-1,1),C(1,-1).
(1)写出点B,D的坐标.
(2)你发现点A,B,C,D之间有何关系?
18.
如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.
(1)请按下列要求画图:
①将△ABC先向右平移5个单位长度,再向上平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2关于点P成中心对称,直接写出对称中心P点的坐标.
19.如图,在平面直角坐标系中A,B坐标分别为(2,0),(–1,3),若△OAC与△OAB全等.
(1)试尽可能多的写出点C的坐标;
(2)在(1)的结果中请找出关于点(1,0)成中心对称的两个点.
20.如图,△ABC三个顶点的坐标分别为A(2,4),B(2,1),C(5,3).
(1)请在网格中,画出△ABC关于原点对称的△A1B1C1;
(2)请在网格中,过点A画一条直线AD,将△ABC分成面积相等的两部分,与x轴相交于点D,并写出点D的坐标.
21.如图所示,在平面直角坐标系中,△PQR是由△ABC经过某种变换后得到的图形.
⑴仔细观察点A和点P,点B和点Q,点C和点R的坐标之间的关系,在这种变换下分别写出这六个点的坐标,从中你发现什么特征?请你用文字语言将你发现的特征表达出来;
⑵若△ABC内有一点M(2a+5,-1-3b)经过变换后,在△PRQ内的坐标为(-3,-2),根据你发现的特征,求关于x的方程2-ax=bx-3的解.
22.如图,已知点A(2,3)和直线y=x.
(1)分别写出点A关于直线y=x的对称点B和关于原点的对称点C的坐标;
(2)若D是点B关于原点的对称点,判断四边形ABCD的形状,并说明理由.
23.阅读下列材料并完成题目:
类似于平移变换是在原有横、纵坐标上加减一个数,在平面直角坐标系xOy中,点P(x,y)经过变换φ得到P′(x′,y′),把这种变换记作φ(x,y)=(x′,y′),其中(a,b为常数),例如:当a=1,且b=1时,则φ(﹣2,3)=(1,﹣5).
(1)①当a=2,且b=1时,φ(﹣2,1)=
.
②若φ(3,1)=(﹣3,﹣3),则a=
,b=
.
(2)点P(2,1)经过变换φ得到点P′(x′,y′),若点P′与点P关于原点对称,求a和b的值.
(3)对任意横、纵坐标满足二元一次方程2x﹣y=0的点P(x,y),点P经过变换φ得到点P′(x′,y′),若点P与点P′重合,求a和b的值.
答案
一、选择题
1.
C
2.
D
3.
B
4.
D
5.
C
6.
A
7.
C
8.
D
9.
A
10.
C
二、填空题
11.
(-5,8)
12.
1
13.
Y=-x2-2x+3(写成顶点式也对)
14.
(-1,1) , (-4,-1) , (-2,-2)
15.
1
16.
x=-2
三、解答题
17.
解:(1)点B的坐标为(2,1),点D的坐标为(-2,-1).
(2)点A与点C关于原点对称,点B与点D关于原点对称.
18.
(1)
解:①△A1B1C1如图所示.②△A2B2C2如图所示.
(2)
解:△A1B1C1与△A2B2C2关于点P成中心对称,如图,点P的坐标是(2.5,0.5).
19.
(1)(3,3)或(–1,–3)或(3,–3);(2)(–1,–3)、(3,3)
20.解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,直线AD即为所求;点D的坐标为(5,0).
21.
⑴A(4,3),B(3,1),C(1,2),P(-4,-3),Q(-3,-1),R(-1,-2),△ABC所在平面上各点与△PQR所在平面的对应点关于原点对称;⑵x=-
22.
解:(1)B(3,2),C(-2,-3).
(2)四边形ABCD是矩形.
理由:∵点B(3,2)关于原点的对称点为D(-3,-2).又∵点B和点D关于原点对称,∴BO=DO.同理AO=CO,∴四边形ABCD是平行四边形.∵点A关于直线y=x的对称点为B,点A关于原点的对称点为C,∴AC=BD,∴四边形ABCD是矩形.
23.
(1)①(﹣3,﹣5);②﹣1,0;(2);(3),.
试卷第8页,总8页
同课章节目录
