23.2.2 中心对称图形自学自测 2021--2022学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 23.2.2 中心对称图形自学自测 2021--2022学年人教版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 286.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 15:21:19 | ||
图片预览

文档简介
23.2.2
中心对称图形自学自测
一、选择题
1.如图,△ABC是一个中心对称图形的一部分,点O是对称中心,A和B是对应点,∠C=90°,那么将这个图形补充完整后是
(
)
A.矩形
B.菱形
C.正方形
D.梯形
2.点P(-2,3)关于坐标原点对称的点的坐标是(
)
A.(3,-2)
B.(2,-3)
C.(-2,-3)
D.(2,3)
3.
用完全相同的两个含30°角的直角三角板拼成的四边形是中心对称图形的个数为?( )
A.1 ????B.2 ????C.3 ????D.4
4.观察下列图形,是中心对称图形的是(
)
A.
B.
C.
D.
5.
已知四边形ABCD中,对角线AC与BD相交于点O,添加某个条件使四边形ABCD既是中心对称图形又是轴对称图形,则符合的条件是?( )
A.OA=OC,OB=OD ????B.AC=BD
C.AC⊥BD ????
D.OA=OC=OB=OD
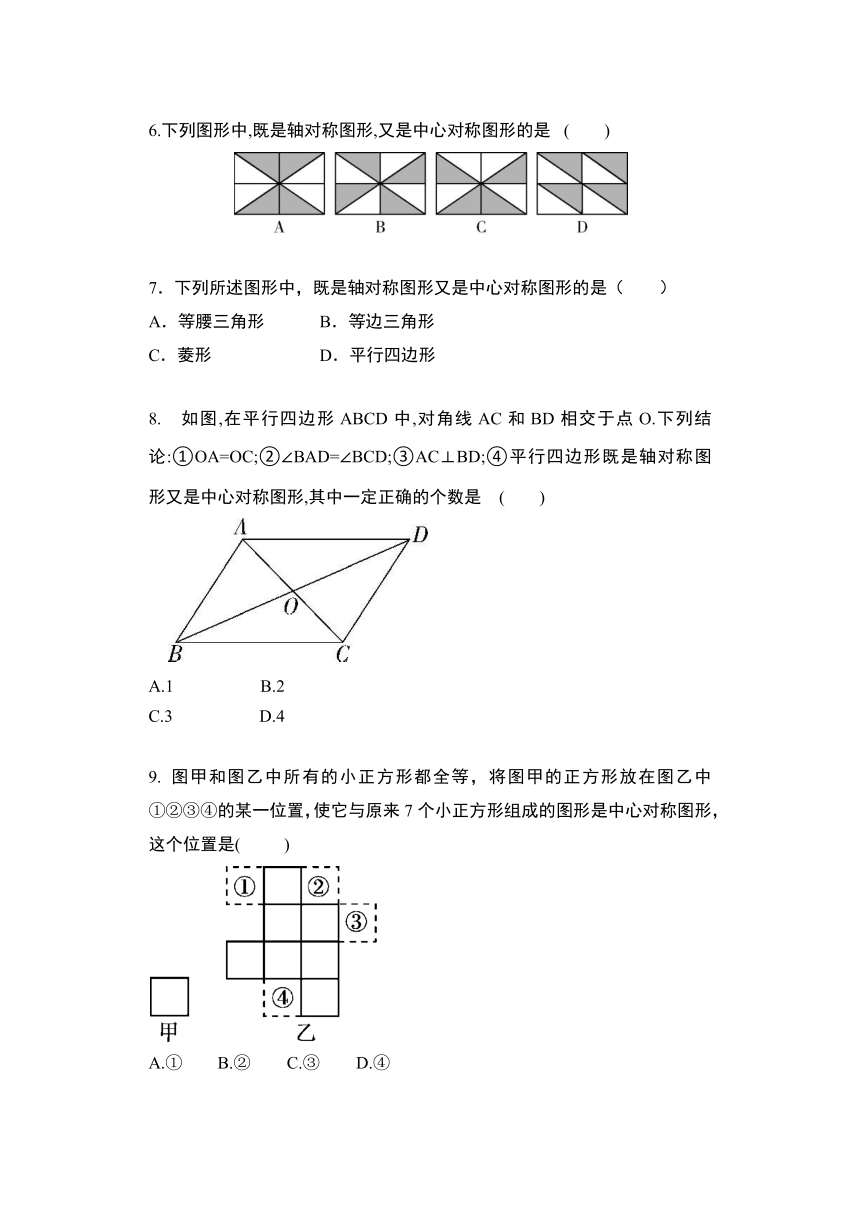
6.下列图形中,既是轴对称图形,又是中心对称图形的是
(
)
7.下列所述图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形
B.等边三角形
C.菱形
D.平行四边形
8.
如图,在平行四边形ABCD中,对角线AC和BD相交于点O.下列结论:①OA=OC;②∠BAD=∠BCD;③AC⊥BD;④平行四边形既是轴对称图形又是中心对称图形,其中一定正确的个数是?( )
?
A.1 ????B.2 ????
C.3 ????D.4
9.
图甲和图乙中所有的小正方形都全等,将图甲的正方形放在图乙中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是(
)
A.①
B.②
C.③
D.④
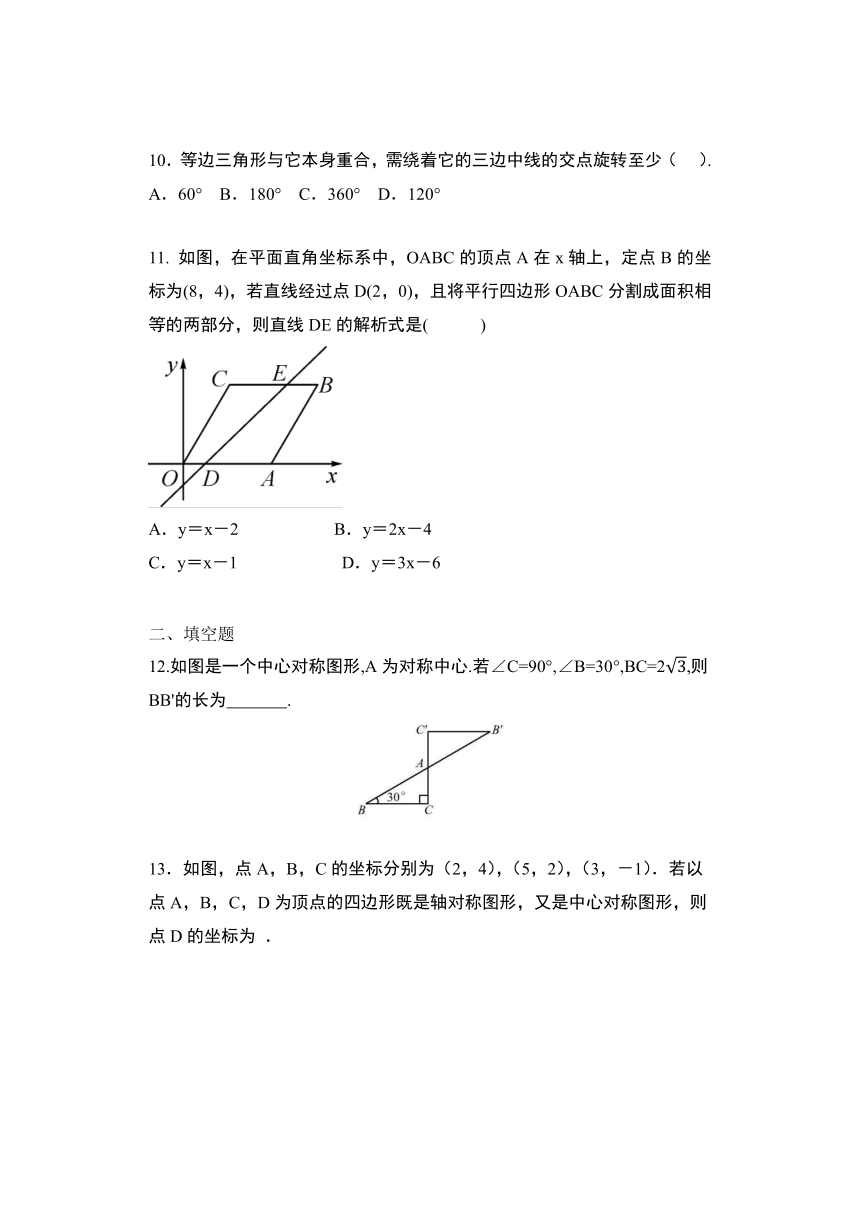
10.等边三角形与它本身重合,需绕着它的三边中线的交点旋转至少(???
).
A.60°
B.180°
C.360°
D.120°
11.
如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的解析式是(
)
A.y=x-2
B.y=2x-4
C.y=x-1
D.y=3x-6
二、填空题
12.如图是一个中心对称图形,A为对称中心.若∠C=90°,∠B=30°,BC=2,则BB'的长为
.?
13.如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为
.
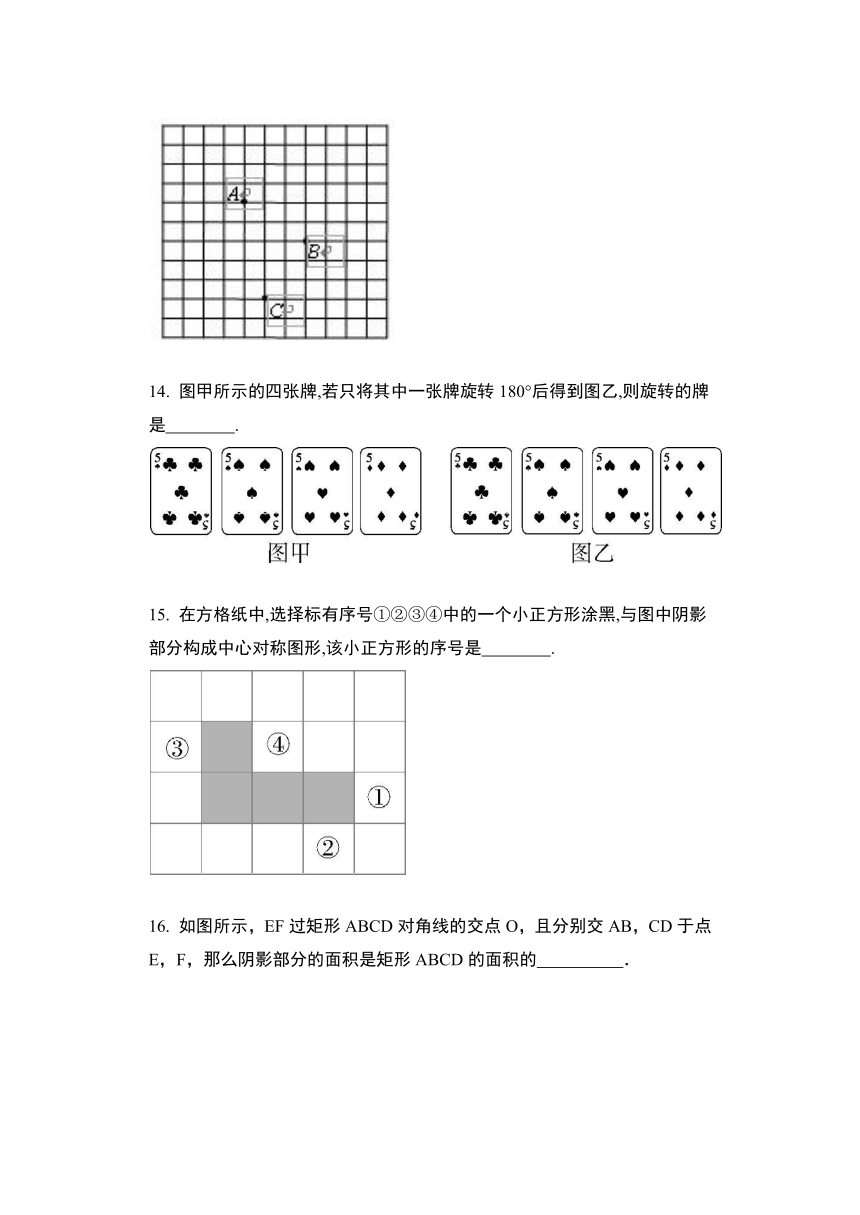
14.
图甲所示的四张牌,若只将其中一张牌旋转180°后得到图乙,则旋转的牌是 ????.
15.
在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是 ????.
16.
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD的面积的
.
三、解答题
17.如图是一个中心对称图形,点A为对称中心.若∠C=90°,∠BAC=30°,BB'=4,求BC的长.
18.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称;
(2)若△ADC的面积为4,求△ABE的面积.
19.
图①、图②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
(2)使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
20.已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD,
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15
cm2,求四边形ABCD的面积.
21.如图,点O是平行四边形ABCD的对称中心,将直线BD绕点O顺时针方向旋转,分别交CD,AB于点E,F.
(1)证明:△DEO≌△BFO;
(2)若BD=2,AD=1,AB=,当BD绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
22.如图,方格纸中有三个点A、B、C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在图甲中作出的四边形是中心对称图形但不是轴对称图形;
(2)在图乙中作出的四边形是轴对称图形但不是中心对称图形;
(3)在图丙中作出的四边形既是轴对称图形又是中心对称图形.
答案
一、选择题
1.
A
2.
B
3.
C
4.
D
5.
D
6.
A
7.
C
8.
B
9.
C
10.
D
11.
?A
二、填空题
12.
8
13.(0,1)
14.
方块5
15.
②
16.
三、解答题
17.
BC=1.
18.
解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8.
19.
(1)
轴对称图形如图①所示.(答案不唯一)
(2)
中心对称图形如图②所示.(答案不唯一)
20.
根据成中心对称图形的性质知OA=OC,OB=OD.根据平行四边形对角线互相平分,所以可以得到四边形ABCD为平行四边形;△AOB的面积为15
cm2,则△ABC面积等于△AOB面积的2倍,因为点O为平行四边形的中心,所以△ABC的高等于△AOB高的2倍,所以S△ABC
=30,所以四边形ABCD的面积是60.
(1)∵AOB与△COD关于点O成中心对称,∴OA=OC,OB=OD.
∴四边形ABCD为平行四边形.
(2)四边形ABCD的面积为60
cm2.
21.解:(1)在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.
又∵点O是平行四边形ABCD的对称中心,
∴OD=OB,∴△DEO≌△BFO(AAS).
(2)四边形AECF是菱形,理由:∵在△ABD中,BD=2,AD=1,AB=,∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°.
∵OD=OB=BD=1,∴AD=OD,
∴△OAD是等腰直角三角形,
∴∠AOD=45°.当直线BD绕点O顺时针旋转45°时,即∠DOE=45°,∴∠AOE=90°.
∵△DEO≌△BFO,∴OE=OF,
又∵点O是平行四边形ABCD的对称中心,
∴OA=OC,
∴四边形AECF是菱形.
22.
解:如图:
试卷第8页,总8页
中心对称图形自学自测
一、选择题
1.如图,△ABC是一个中心对称图形的一部分,点O是对称中心,A和B是对应点,∠C=90°,那么将这个图形补充完整后是
(
)
A.矩形
B.菱形
C.正方形
D.梯形
2.点P(-2,3)关于坐标原点对称的点的坐标是(
)
A.(3,-2)
B.(2,-3)
C.(-2,-3)
D.(2,3)
3.
用完全相同的两个含30°角的直角三角板拼成的四边形是中心对称图形的个数为?( )
A.1 ????B.2 ????C.3 ????D.4
4.观察下列图形,是中心对称图形的是(
)
A.
B.
C.
D.
5.
已知四边形ABCD中,对角线AC与BD相交于点O,添加某个条件使四边形ABCD既是中心对称图形又是轴对称图形,则符合的条件是?( )
A.OA=OC,OB=OD ????B.AC=BD
C.AC⊥BD ????
D.OA=OC=OB=OD
6.下列图形中,既是轴对称图形,又是中心对称图形的是
(
)
7.下列所述图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形
B.等边三角形
C.菱形
D.平行四边形
8.
如图,在平行四边形ABCD中,对角线AC和BD相交于点O.下列结论:①OA=OC;②∠BAD=∠BCD;③AC⊥BD;④平行四边形既是轴对称图形又是中心对称图形,其中一定正确的个数是?( )
?
A.1 ????B.2 ????
C.3 ????D.4
9.
图甲和图乙中所有的小正方形都全等,将图甲的正方形放在图乙中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是(
)
A.①
B.②
C.③
D.④
10.等边三角形与它本身重合,需绕着它的三边中线的交点旋转至少(???
).
A.60°
B.180°
C.360°
D.120°
11.
如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的解析式是(
)
A.y=x-2
B.y=2x-4
C.y=x-1
D.y=3x-6
二、填空题
12.如图是一个中心对称图形,A为对称中心.若∠C=90°,∠B=30°,BC=2,则BB'的长为
.?
13.如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为
.
14.
图甲所示的四张牌,若只将其中一张牌旋转180°后得到图乙,则旋转的牌是 ????.
15.
在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是 ????.
16.
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD的面积的
.
三、解答题
17.如图是一个中心对称图形,点A为对称中心.若∠C=90°,∠BAC=30°,BB'=4,求BC的长.
18.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称;
(2)若△ADC的面积为4,求△ABE的面积.
19.
图①、图②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
(2)使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
20.已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD,
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15
cm2,求四边形ABCD的面积.
21.如图,点O是平行四边形ABCD的对称中心,将直线BD绕点O顺时针方向旋转,分别交CD,AB于点E,F.
(1)证明:△DEO≌△BFO;
(2)若BD=2,AD=1,AB=,当BD绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
22.如图,方格纸中有三个点A、B、C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在图甲中作出的四边形是中心对称图形但不是轴对称图形;
(2)在图乙中作出的四边形是轴对称图形但不是中心对称图形;
(3)在图丙中作出的四边形既是轴对称图形又是中心对称图形.
答案
一、选择题
1.
A
2.
B
3.
C
4.
D
5.
D
6.
A
7.
C
8.
B
9.
C
10.
D
11.
?A
二、填空题
12.
8
13.(0,1)
14.
方块5
15.
②
16.
三、解答题
17.
BC=1.
18.
解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8.
19.
(1)
轴对称图形如图①所示.(答案不唯一)
(2)
中心对称图形如图②所示.(答案不唯一)
20.
根据成中心对称图形的性质知OA=OC,OB=OD.根据平行四边形对角线互相平分,所以可以得到四边形ABCD为平行四边形;△AOB的面积为15
cm2,则△ABC面积等于△AOB面积的2倍,因为点O为平行四边形的中心,所以△ABC的高等于△AOB高的2倍,所以S△ABC
=30,所以四边形ABCD的面积是60.
(1)∵AOB与△COD关于点O成中心对称,∴OA=OC,OB=OD.
∴四边形ABCD为平行四边形.
(2)四边形ABCD的面积为60
cm2.
21.解:(1)在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.
又∵点O是平行四边形ABCD的对称中心,
∴OD=OB,∴△DEO≌△BFO(AAS).
(2)四边形AECF是菱形,理由:∵在△ABD中,BD=2,AD=1,AB=,∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°.
∵OD=OB=BD=1,∴AD=OD,
∴△OAD是等腰直角三角形,
∴∠AOD=45°.当直线BD绕点O顺时针旋转45°时,即∠DOE=45°,∴∠AOE=90°.
∵△DEO≌△BFO,∴OE=OF,
又∵点O是平行四边形ABCD的对称中心,
∴OA=OC,
∴四边形AECF是菱形.
22.
解:如图:
试卷第8页,总8页
同课章节目录
