【优选作业本】卷12 22.1.2 二次函数y-ax2的图像和性质(含解析)
文档属性
| 名称 | 【优选作业本】卷12 22.1.2 二次函数y-ax2的图像和性质(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 14:27:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章
二次函数
22.1
二次函数的图像和性质
22.1.2
二次函数y=ax2的图像和性质
基础夯实练
01
二次函数y=ax2的图像
1.函数y=5x2,y=-9x2,y=x2,y=-10x2图像的共同特征是
(
)
A.开口都向上,且都关于y轴对称.
B.开口都向下,且都关于x轴对称
C.顶点都是原点,且都关于y轴对称
D.顶点都是原点,且都关于x轴对称
2.(易错题)已知四个二次函数的图像如图,那么a1,a2,a3,a4的大小关系是________(请用“>”连接排序)
3.在同一平面直角坐标系中,画出下列函数的图像,并说明这两个图像之间的关系
(1)y=4x2;(2)y=-4x2
02
二次函数y=ax2的性质
4.已知原点是抛物线y=(m+1)x2的最高点,则m的取值范围是
(
)
A.m<-1
B.m<1
C.m>-1
D.m>-2
5.下列关于二次函数y=2x2的说法正确的是
(
)
A.它的图像经过点(-1,-2)
B.它的图像的对称轴是直线x=2
C.当x<0时,y随x的增大而减小
D.当x=0时,y有最大值,为0
6.已知抛物线y=ax2(a>0)经过A(-2,y1),B(1,y2)C(3,y3)三点,则y1,y2,y3的大小关系是________(用“<”连接)
7.(易错题)[教材P32练习改编]已知抛物线y=(m+2)x2与抛物线y=3x2的形状相同,请指出抛物线y=mx2的开口方向、对称轴和顶点坐标.
能力提升练
8.二次函数y=ax2的图像与一次函数y=ax+a的图像在同一平面直角坐标系中的大致图像可能是
(
)
9.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图像,则阴影部分的面积是________
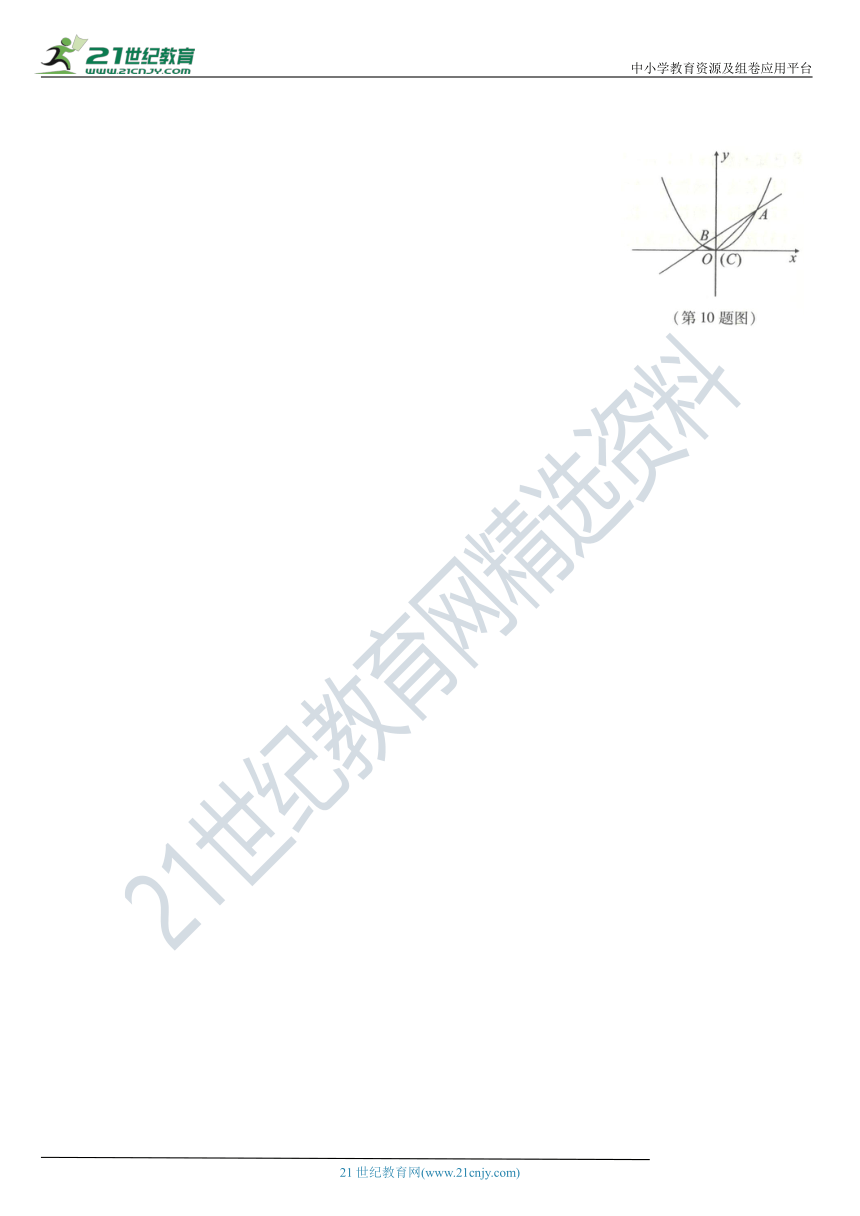
10.如图,已知一次函数y=ax+b(第9题图)的图像上有A,B两点,它们的横坐标分别是3,-1,若二次函数y=x2的图像经过A,B两点
(1)求出一次函数的解析式;
(2)设二次函数图像的顶点为C,求△ABC的面积
????????????????????????????????????????????????????????????
《参考答案及解析》
22.1.2
二次函数y=ax2的图像和性质
1.c【解析】函数y=5x2和y=x2的图像的开口向上,函数y=-9x2和y=-10x2的图像的开口向下,所以选项A和选项B都错误;函数y=5x2,y=-9x2,y=x2,y=-10x2的图像的顶点都是原点,对称轴都是y轴,所以选项D错误.故选C.
2.a1>a2>a3>a4【解析】由图像可知,a1>0,a2>0,a3<0,a4<0,且抛物线y=a1x2的开口小于抛物线y=a2x2的开口,抛物线y=a3x2的开口大于抛物线y=a4x2的开口,所以a1>a2>0,a4a2>a3>a4
【易错总结】对二次函数图像的开口大小与系数的对应关系理解有误二次函数图像的开口大小仅与二次项的系数的绝对值有关,绝对值越大其开口越小,绝对值越小其开口越大,不要记反了
【一题多解】
如答图.因为直线x=1与四条抛物线的交点从上到下依次为点A(1,a1),B(1,a2),C(1,a3),D(1,a4),所以a1>a2>a3>a4
3.解:列表:
描点、连线,如答图
观察图像可发现,二次函数y=-4x2的图像可由二次函数y=4x2的图像以x轴为对称轴向下翻折得到
4.A【解析】∵原点是抛物线y=(m+1)x2的最高点,∴m+1<0,即m<-1.故选A.
5.C【解析】A.当x=-1时,y=2×(-1)2=2≠-2,此选项错误.B.它的图像的对称轴是直线x=0,此选项错误C.当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大,此选项正确.D.当x=0时,y有最小值,为,此选项错误.故选C.
6.y20)经过A(-2,y1),B(1,y2),C(3,y3)三点,∴y1=4a,y2=a,y3=9a.∵a>0,∴a<4a<9a,∴y2【一题多解】
设a=1,则y=x2.将A,B,C三点的坐标分别代入,得y1=4,y2=1,y3=9,∴y2【方法解读】比较几个函数值的大小的方法
(1)代入比较法:先将所给的几个点的横坐标代入函数解析式式,计算出对应的纵坐标的值,再比较纵坐标的大小即可.
(2)增减性比较法:当所给的几个点在抛物线的对称轴的同一侧时,直接用增减性即可比较;当所给的几个点不在抛物线的对称轴的同一侧时,需先利用抛物线的对称性将点转化到对称轴的同一侧,再利用二次函数的增减性来比较.
7.解:∵抛物线y=(m+2)x2与抛物线y=3x2的形状相同,∴m+2=±3,∴m=1或m=-5.
当m=1时,抛物线为y=x2,其开口向上,对称轴是y轴,顶点坐标为(0,0);
当m=-5时,抛物线为y=-5x2,其开口向下对称轴是y轴顶点坐标为(0,0)
【易错总结】对二次函数图像的形状相同理解错误
抛物线y=ax2中a决定开口方向,lal决定开口大小若两条抛物线的形状相同,则说明这两条抛物线的开口大小相同此题易忽略m+2=-3的情况,从而导致漏解
8.D
【解析】一次函数y=ax+a的图像与x轴交于点(-1,0),所以排除A,B选项.当a>0时,二次函数y=ax2的图像的开口向上,一次函数y=+a的图像经过第一、二、三象限,D选项符合;当a<0时,二次函数y=x2的图像的开口向下,一次函数y=ax+a的图像经过第二、三、四象限,所以排除C选项.故选D
【方法解读】解决双函数图像问题的两种方法
(1)分类讨论法:按系数的正负进行讨论;(2)逐项排除法:先假定选项中某一函数的图像正确,再判断另一函数的图像是否合理
9.8【解析】因为函数y=2x2与y=-2x2的图像关于x轴对称,所以阴影部分的面积是正方形面积的一半.又因为边长为4的正方形的面积为16,所以阴影部分的面积是8.
10.解:(1)当x=3时,y=x2=3,∴点A的坐标为(3,3);
当x=-1时,y=x2=,
∴点B的坐标为(-1,)
分别将点A(3,3),B(-1,)的坐标代入y=ax+b,
可得
eq
\b
\lc\{(\a
\al
\co1(3a+b=3,
-a+b=))
,解得
eq
\b
\lc\{(\a
\al
\co1(a=,b=1))
∴一次函数的解析式为y=x+1
(2)∵二次函数的解析式为y=x2,
∴二次函数图像的顶点C的坐标为(0,0)
设一次函数的图像与x轴的交点为D,则点D的坐标为
eq
\b
\bc\((-,0)
,∴DC=
∴S△ABC=S△ADC-S△BDC=××3-××=-=2
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第二十二章
二次函数
22.1
二次函数的图像和性质
22.1.2
二次函数y=ax2的图像和性质
基础夯实练
01
二次函数y=ax2的图像
1.函数y=5x2,y=-9x2,y=x2,y=-10x2图像的共同特征是
(
)
A.开口都向上,且都关于y轴对称.
B.开口都向下,且都关于x轴对称
C.顶点都是原点,且都关于y轴对称
D.顶点都是原点,且都关于x轴对称
2.(易错题)已知四个二次函数的图像如图,那么a1,a2,a3,a4的大小关系是________(请用“>”连接排序)
3.在同一平面直角坐标系中,画出下列函数的图像,并说明这两个图像之间的关系
(1)y=4x2;(2)y=-4x2
02
二次函数y=ax2的性质
4.已知原点是抛物线y=(m+1)x2的最高点,则m的取值范围是
(
)
A.m<-1
B.m<1
C.m>-1
D.m>-2
5.下列关于二次函数y=2x2的说法正确的是
(
)
A.它的图像经过点(-1,-2)
B.它的图像的对称轴是直线x=2
C.当x<0时,y随x的增大而减小
D.当x=0时,y有最大值,为0
6.已知抛物线y=ax2(a>0)经过A(-2,y1),B(1,y2)C(3,y3)三点,则y1,y2,y3的大小关系是________(用“<”连接)
7.(易错题)[教材P32练习改编]已知抛物线y=(m+2)x2与抛物线y=3x2的形状相同,请指出抛物线y=mx2的开口方向、对称轴和顶点坐标.
能力提升练
8.二次函数y=ax2的图像与一次函数y=ax+a的图像在同一平面直角坐标系中的大致图像可能是
(
)
9.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图像,则阴影部分的面积是________
10.如图,已知一次函数y=ax+b(第9题图)的图像上有A,B两点,它们的横坐标分别是3,-1,若二次函数y=x2的图像经过A,B两点
(1)求出一次函数的解析式;
(2)设二次函数图像的顶点为C,求△ABC的面积
????????????????????????????????????????????????????????????
《参考答案及解析》
22.1.2
二次函数y=ax2的图像和性质
1.c【解析】函数y=5x2和y=x2的图像的开口向上,函数y=-9x2和y=-10x2的图像的开口向下,所以选项A和选项B都错误;函数y=5x2,y=-9x2,y=x2,y=-10x2的图像的顶点都是原点,对称轴都是y轴,所以选项D错误.故选C.
2.a1>a2>a3>a4【解析】由图像可知,a1>0,a2>0,a3<0,a4<0,且抛物线y=a1x2的开口小于抛物线y=a2x2的开口,抛物线y=a3x2的开口大于抛物线y=a4x2的开口,所以a1>a2>0,a4
【易错总结】对二次函数图像的开口大小与系数的对应关系理解有误二次函数图像的开口大小仅与二次项的系数的绝对值有关,绝对值越大其开口越小,绝对值越小其开口越大,不要记反了
【一题多解】
如答图.因为直线x=1与四条抛物线的交点从上到下依次为点A(1,a1),B(1,a2),C(1,a3),D(1,a4),所以a1>a2>a3>a4
3.解:列表:
描点、连线,如答图
观察图像可发现,二次函数y=-4x2的图像可由二次函数y=4x2的图像以x轴为对称轴向下翻折得到
4.A【解析】∵原点是抛物线y=(m+1)x2的最高点,∴m+1<0,即m<-1.故选A.
5.C【解析】A.当x=-1时,y=2×(-1)2=2≠-2,此选项错误.B.它的图像的对称轴是直线x=0,此选项错误C.当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大,此选项正确.D.当x=0时,y有最小值,为,此选项错误.故选C.
6.y2
设a=1,则y=x2.将A,B,C三点的坐标分别代入,得y1=4,y2=1,y3=9,∴y2
(1)代入比较法:先将所给的几个点的横坐标代入函数解析式式,计算出对应的纵坐标的值,再比较纵坐标的大小即可.
(2)增减性比较法:当所给的几个点在抛物线的对称轴的同一侧时,直接用增减性即可比较;当所给的几个点不在抛物线的对称轴的同一侧时,需先利用抛物线的对称性将点转化到对称轴的同一侧,再利用二次函数的增减性来比较.
7.解:∵抛物线y=(m+2)x2与抛物线y=3x2的形状相同,∴m+2=±3,∴m=1或m=-5.
当m=1时,抛物线为y=x2,其开口向上,对称轴是y轴,顶点坐标为(0,0);
当m=-5时,抛物线为y=-5x2,其开口向下对称轴是y轴顶点坐标为(0,0)
【易错总结】对二次函数图像的形状相同理解错误
抛物线y=ax2中a决定开口方向,lal决定开口大小若两条抛物线的形状相同,则说明这两条抛物线的开口大小相同此题易忽略m+2=-3的情况,从而导致漏解
8.D
【解析】一次函数y=ax+a的图像与x轴交于点(-1,0),所以排除A,B选项.当a>0时,二次函数y=ax2的图像的开口向上,一次函数y=+a的图像经过第一、二、三象限,D选项符合;当a<0时,二次函数y=x2的图像的开口向下,一次函数y=ax+a的图像经过第二、三、四象限,所以排除C选项.故选D
【方法解读】解决双函数图像问题的两种方法
(1)分类讨论法:按系数的正负进行讨论;(2)逐项排除法:先假定选项中某一函数的图像正确,再判断另一函数的图像是否合理
9.8【解析】因为函数y=2x2与y=-2x2的图像关于x轴对称,所以阴影部分的面积是正方形面积的一半.又因为边长为4的正方形的面积为16,所以阴影部分的面积是8.
10.解:(1)当x=3时,y=x2=3,∴点A的坐标为(3,3);
当x=-1时,y=x2=,
∴点B的坐标为(-1,)
分别将点A(3,3),B(-1,)的坐标代入y=ax+b,
可得
eq
\b
\lc\{(\a
\al
\co1(3a+b=3,
-a+b=))
,解得
eq
\b
\lc\{(\a
\al
\co1(a=,b=1))
∴一次函数的解析式为y=x+1
(2)∵二次函数的解析式为y=x2,
∴二次函数图像的顶点C的坐标为(0,0)
设一次函数的图像与x轴的交点为D,则点D的坐标为
eq
\b
\bc\((-,0)
,∴DC=
∴S△ABC=S△ADC-S△BDC=××3-××=-=2
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
