第9章统计 单元基础检测题-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课前检测(Word版含解析)(含解析)
文档属性
| 名称 | 第9章统计 单元基础检测题-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课前检测(Word版含解析)(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览


文档简介
人教A版第九章统计单元基础检测题
一、单选题
1.医生要检验人血液中血脂的含量,采取的调查方法应该是( )
A.普查 B.抽样调查 C.既不能普查也不能抽样调查 D.普查与抽样调查都可以
2.某校高三一班有学生54人,二班有学生42人,现在要用分层随机抽样的方法从两个班抽出16人参加军训表演,则两班分别被抽取的人数是( )
A.8,8 B.10,6 C.9,7 D.12,4
3.从编号为01,02,…,49,50的50个个体中利用下面的随机数表选取5个个体,选取方法从随机数表第1行第5列的数开始由左到右依次抽取,则选出来的第5个个体的编号为( )
7816 6572 0812 1463 0782 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.14 B.07
C.32 D.43
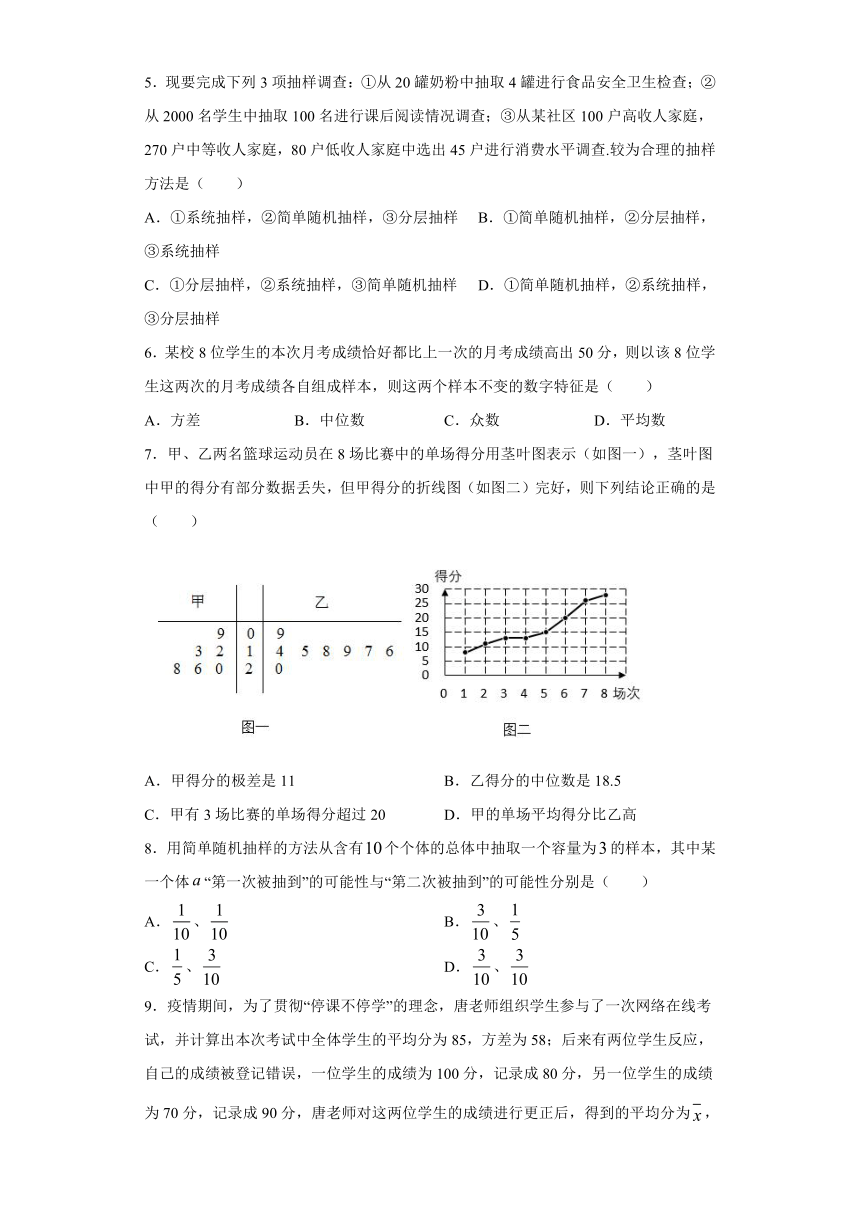
4.2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化、国际化、便利化的营商环境,不断提高贸易便利化水平,外贸稳规模、提质量、转动力取得阶段性成效,进出口保持稳中提质的发展势头,如图是某省近五年进出口情况统计图,下列描述错误的是( )
A.这五年,2015年出口额最少 B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降 D.这五年,2019年进口增速最快
5.现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从2000名学生中抽取100名进行课后阅读情况调查;③从某社区100户高收人家庭,270户中等收人家庭,80户低收人家庭中选出45户进行消费水平调查.较为合理的抽样方法是( )
A.①系统抽样,②简单随机抽样,③分层抽样 B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样 D.①简单随机抽样,②系统抽样,③分层抽样
6.某校8位学生的本次月考成绩恰好都比上一次的月考成绩高出50分,则以该8位学生这两次的月考成绩各自组成样本,则这两个样本不变的数字特征是( )
A.方差 B.中位数 C.众数 D.平均数
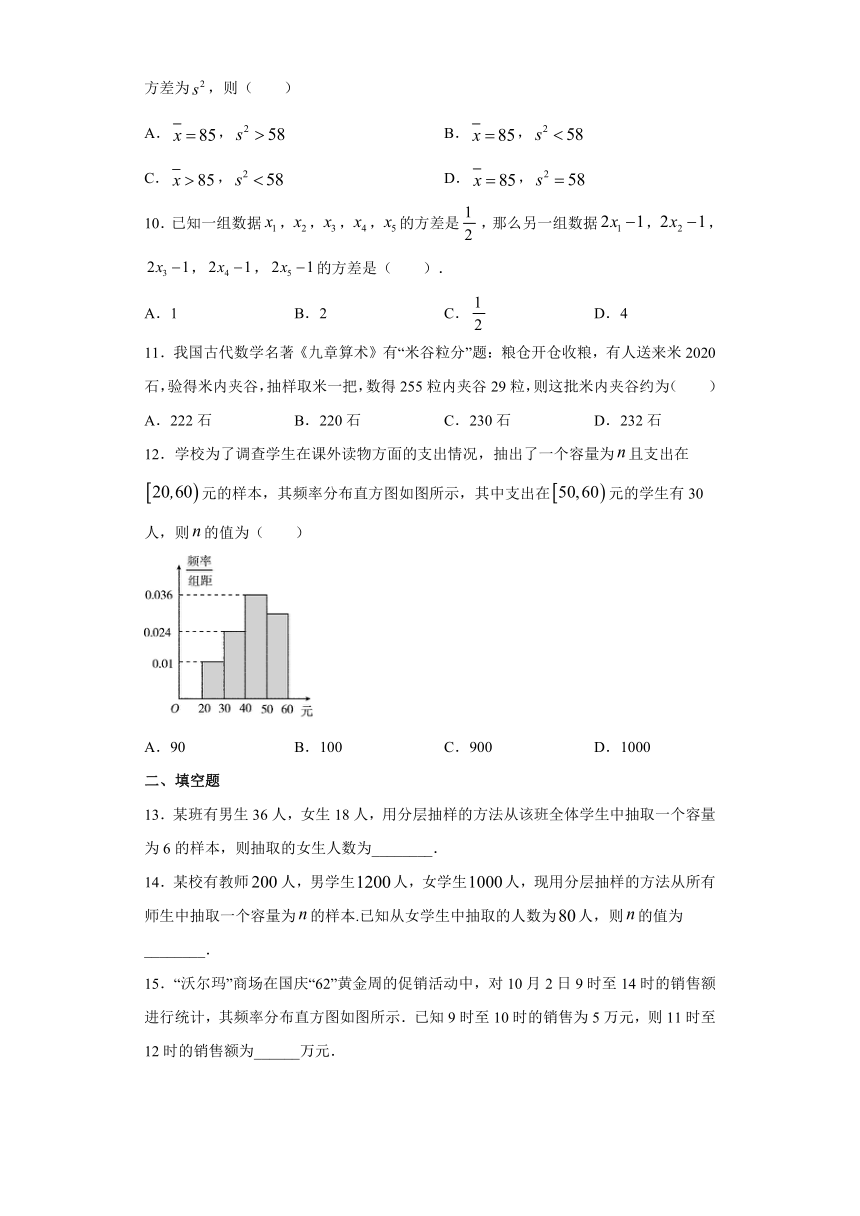
7.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(如图一),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(如图二)完好,则下列结论正确的是( )
A.甲得分的极差是11 B.乙得分的中位数是18.5
C.甲有3场比赛的单场得分超过20 D.甲的单场平均得分比乙高
8.用简单随机抽样的方法从含有个个体的总体中抽取一个容量为的样本,其中某一个体“第一次被抽到”的可能性与“第二次被抽到”的可能性分别是( )
A.、 B.、
C.、 D.、
9.疫情期间,为了贯彻“停课不停学”的理念,唐老师组织学生参与了一次网络在线考试,并计算出本次考试中全体学生的平均分为85,方差为58;后来有两位学生反应,自己的成绩被登记错误,一位学生的成绩为100分,记录成80分,另一位学生的成绩为70分,记录成90分,唐老师对这两位学生的成绩进行更正后,得到的平均分为,方差为,则( )
A., B.,
C., D.,
10.已知一组数据,,,,的方差是,那么另一组数据,,,,的方差是( ).
A.1 B.2 C. D.4
11.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米2020石,验得米内夹谷,抽样取米一把,数得255粒内夹谷29粒,则这批米内夹谷约为( )
A.222石 B.220石 C.230石 D.232石
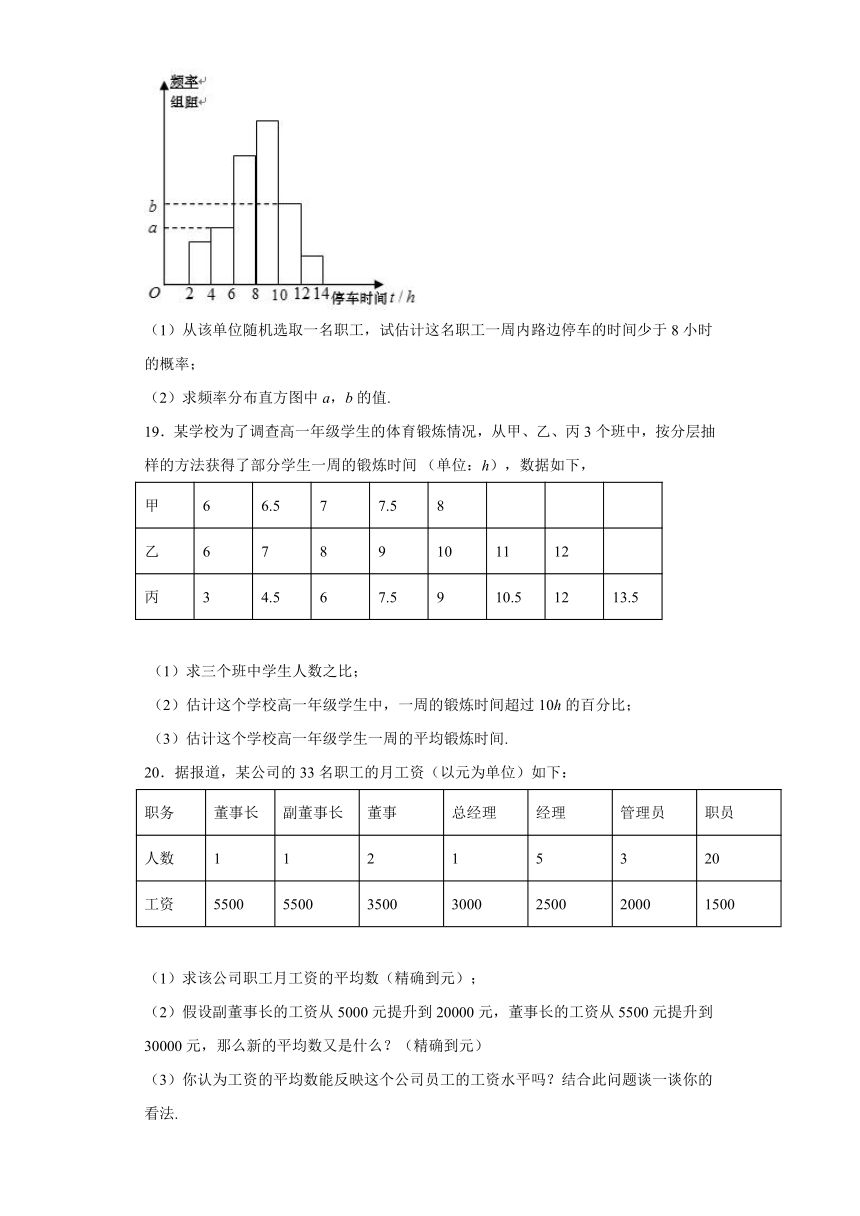
12.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为且支出在元的样本,其频率分布直方图如图所示,其中支出在元的学生有30人,则的值为( )
A.90 B.100 C.900 D.1000
二、填空题
13.某班有男生36人,女生18人,用分层抽样的方法从该班全体学生中抽取一个容量为6的样本,则抽取的女生人数为________.
14.某校有教师人,男学生人,女学生人,现用分层抽样的方法从所有师生中抽取一个容量为的样本.已知从女学生中抽取的人数为人,则的值为________.
15.“沃尔玛”商场在国庆“62”黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售为5万元,则11时至12时的销售额为______万元.
16.已知甲、乙两组数据如茎叶图所示,若两组数据的中位数相同,平均数也相同,那么m+n=________.
三、解答题
17.某中学从40名学生中选1名学生作为某男篮拉拉队成员,采用下面两种方法选取.
方法一:将40名学生按1~40进行编号,相应制作1~40的40个号签,把这40个号签放在一个暗箱中搅拌均匀,最后随机地从中抽取1个号签,与这个号签号码一致的学生幸运入选;方法二;将39个白球与1个红球混合放在一个暗箱中搅匀,让40名学生逐一从中摸取l个球,摸到红球的学生成为拉拉队成员.
试问这两种方法是否都是抽签法?为什么?
18.为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:
(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中a,b的值.
19.某学校为了调查高一年级学生的体育锻炼情况,从甲、乙、丙3个班中,按分层抽样的方法获得了部分学生一周的锻炼时间?(单位:h),数据如下,
甲 6 6.5 7 7.5 8
乙 6 7 8 9 10 11 12
丙 3 4.5 6 7.5 9 10.5 12 13.5
?(1)求三个班中学生人数之比;
?(2)估计这个学校高一年级学生中,一周的锻炼时间超过10h的百分比;
?(3)估计这个学校高一年级学生一周的平均锻炼时间.
20.据报道,某公司的33名职工的月工资(以元为单位)如下:
职务 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5500 3500 3000 2500 2000 1500
(1)求该公司职工月工资的平均数(精确到元);
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数又是什么?(精确到元)
(3)你认为工资的平均数能反映这个公司员工的工资水平吗?结合此问题谈一谈你的看法.
21.我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为,,,,,其频率分布直方图如图所示,请你解答下列问题:
(1)求的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
22.2018年茂名市举办“好心杯”少年美术书法作品比赛,某赛区收到200件参赛作品,为了解作品质量,现从这些作品中随机抽取12件作品进行试评.成绩如下:67,82,78,86,96,81,73,84,76,59,85,93.
(1)求该样本的中位数和方差;
(2)若把成绩不低于85分(含85分)的作品认为为优秀作品,现在从这12件作品中任意抽取3件,求抽到优秀作品的件数的分布列和期望.
参考答案
1.B
【分析】
根据普查和抽样调查的特点进行判断即可.
【详解】
只能抽样调查,如果普查,人也活不了了,
故选:B.
【点睛】
本题考查的是调查方法的选择,正确选择调查方法要根据调查方式的优缺点再结合实际情况去分析.
2.C
【分析】
先计算每个个体被抽到的概率,再用每层的个体数乘以每个个体被抽到的概率,即得到该层应抽取的个体数.
【详解】
抽样比为,则两班分别被抽取的人数是, .
故从一班抽出9人,从二班抽出7人.
故选:C.
【点睛】
本题考查分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数.
3.D
【分析】
根据随机数表的取法,从第1行第5列的数开始两个两个的读数,不大于50的保留,大于50的去掉,保留到第5个即得.
【详解】
由题意知选定的第一个数为65(第1行的第5列和第6列),按由左到右选取两位数(大于50的跳过、重复的不选取),前5个个体编号为08,12,14,07,43.故选出来的第5个个体的编号为43.
故选:D.
【点睛】
本题考查随机数表,掌握随机数表取数规则即可.
4.C
【分析】
观察白色条形图可分析选项A,观察5组条形图可分析选项B,观察虚线折线图可分析选项C,观察实线折线图可分析选项D.
【详解】
对于选项A,观察5个白色条形图可知,这五年中2015年出口额最少,故A正确;
对于选项B,观察五组条形图可得,2015年出口额比进口额稍低,
但2016年至2019年出口额都高于进口额,并且2017年和2018年出口额都明显高于进口额,
故这五年,出口总额比进口总额多,故B正确;
对于选项C,观察虚线折线图可知,2015年到2016年出口增速是上升的,故C错误;
对于选项D,从图中可知,实线折线图2019年是最高的,即2019年进口增速最快,故D正确.
故选:C.
【点睛】
本题考查条形统计图的性质应用,考查数据分析能力,属于基础题.
5.D
【分析】
根据系统抽样、简单随机抽样、分层抽样的概念判断.
【详解】
在①中,由于总体个数较少,故采用简单随机抽样即可;
在②中,由于总体个数较多,故采用系统抽样较好;
在③中,由于高收入家庭、中等收入家庭和低收人家庭的消费水平差异明显,
故采用分层抽样较好.
故选:D.
【点睛】
本题考查抽样的概念,掌握系统抽样、简单随机抽样、分层抽样的概念是解题关键.
6.A
【分析】
通过方差公式分析可知方差没有改变,中位数、众数和平均数都发生了改变.
【详解】
由题可知,中位数和众数、平均数都有变化.
本次和上次的月考成绩相比,成绩和平均数都增加了50,所以没有改变,
根据方差公式可知方差不变.
故选:A
【点睛】
本题主要考查样本的数字特征,意在考查学生对这些知识的理解掌握水平.
7.D
【分析】
根据茎叶图,折线图整合数据,判断选项.
【详解】
甲的极差为,故A选项不符合题意.
乙的中位数为,故选项B不符合题意.
甲得分的折线图可知甲运动员得分有2次超过20,故选项C不符合题意.
根据茎叶图和折线图可知,甲的单场平均得分大于,乙的单场平均得分为,故甲的单场平均得分比乙高.
故选:D.
【点睛】
本题考查对茎叶图,折线图的分析整合能力,属于基础题.
8.A
【分析】
根据抽样中,每个个体在每一次被抽到的概率都是相等的,由此可得出结果.
【详解】
在抽样过程中,个体每一次被抽中的概率是相等的,因为总体容量为,
故个体“第一次被抽到”的可能性与“第二次被抽到”的可能性均为,
故选:A.
【点睛】
本题考查抽样中概率的计算,属于基础题.
9.A
【分析】
由于,,,再根据平均数和方差的计算公式可得选项.
【详解】
由于,因此更正前后样本的平均数不发生改变,即;
由于,,因此更正后样本的方差变大,即;故选:A.
【点睛】
本题考查平均数和方差的计算原理,属于基础题.
10.B
【分析】
根据数据关系得方差关系,即可求解.
【详解】
因为数据,,,,的方差是数据,,,,的方差的4倍,所以数据,,,,的方差是
故选:B
【点睛】
本题考查方差、新旧数据方差关系,考查基本分析求解能力,属基础题.
11.C
【分析】
根据米255粒内夹谷29粒,求得频率,再根据频率计算这批米内夹谷量.
【详解】
根据米255粒内夹谷29粒,则频率为,
则这批米内夹谷约为(石).
故选:C.
【点睛】
本题考查了用样本估计总体,属于基础题.
12.B
【分析】
先由频率分布直方图求出支出在元的频率,然后根据频率、频数和样本容量间的关系求解即可得到答案.
【详解】
由频率分布直方图可得支出在元的频率为,
因此,
解得.
故选:B.
【点睛】
频率分布直方图直观形象地表示了样本的频率分布,从这个直方图上可以求出样本数据在各个组的频率分布.本题考查识图、用图和计算能力,属于基础题.
13.2
【分析】
分层抽样的抽取比例为,抽取的女生人数为抽取比例女生人数.
【详解】
由题意知:分层抽样的抽取比例为,
抽取的女生人数为.
故答案为:2.
【点睛】
本题考查了分层抽样方法,熟练掌握分层抽样的定义是关键,属于基础题.
14.
【分析】
根据女学生的入样比与总体的入样比相等列等式可求出的值.
【详解】
由于女学生的入样比与总体的入样比相等,则,解得.
故答案为:.
【点睛】
本题考查分层抽样的定义和方法,根据每层的入样比与总体的入样比相等列等式是解答的关键,考查运算求解能力,属于基础题.
15.20
【分析】
根据频率分布直方图计算出时至时的销售额.
【详解】
由于时至时的销售额为万元,根据频率分布直方图可知时至时的销售额为万元.
故答案为:
【点睛】
本小题主要考查频率分布直方图,属于基础题.
16.11
【分析】
由两组数据平均数相同有,再由中位数相等可得,即可求n,所以的值可得
【详解】
由平均数相同知:,有
对于乙:,32,34,38,则中位数为
∵两组数据的中位数相同
∴有
即有
故有
故答案为:11
【点睛】
本题考查了利用茎叶图,结合平均数、中位数概念求参数
17.见解析
【分析】
根据抽签法的概念进行判断即可.
【详解】
解:抽签法抽样时给总体中的N个个体编号各不相同,由此可知方法一是抽签法,因为抽签法要求所有的号签编号互不相同,而方法二中39个白球无法相互区分,故方法二不是抽签法.
这两种方法的相同之处在于每名学生被选中的机会都相等.
【点睛】
本题考查抽签法的概念,是基础题.
18.(1);(2),.
【分析】
(1)由频率分布表即可得解;
(2)由频率分布直方图中小矩形的高为频率与组距的比值,观察频率分布表的数据即可得解.
【详解】
解:(1)记“从该单位随机选取一名职工,这名职工该周路边停车的时间少于8小时”为事件A,则;
(2)由频率分布表可得:区间的频数为8, 则,
区间的频数为12,则.
【点睛】
本题考查了频率分布表及频率分布直方图,属基础题.
19.(1)(2)25%(3)8.2h
【分析】
(1)样本中人数比例与总体中人数比例相等;
(2)求出样本中一周的锻炼时间超过10h的人数,求得比例,再估计年段的比例;
(3)求出样本的平均数,从而估计年段的平均数.
【详解】
(1)三个班中学生人数之比为.
(2)样本中一周的锻炼时间超过10h的有5个,
因此一周的锻炼时间超过10h的百分比为.
估计该校高一年级学生中,一周的锻炼时间超过10h的百分比为25%.
?(3)样本中甲、乙、丙三个班级的平均锻炼时间分别为7h,9h,8.25h,
则样本平均数为.
估计该校高一年级学生一周的平均锻炼时间为8.2h.
【点睛】
本题考查频率、平均数的计算,考查数据处理能力,属于基础题.
20.(1)2091元 (2)3288元 (3)不能反映这个公司员工的工资水平.见解析
【分析】
(1)根据平均数的计算公式计算即可;
(2)根据平均数的计算公式计算即可;
(3)根据某些个题对总体的影响情况来说明.
【详解】
解:(1)平均数是
(元).
(2)平均数是
(元).
(3)在这个问题中,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数偏差较大,所以平均数不能反映这个公司员工的工资水平.
【点睛】
本题考查平均数的计算,以及个体对总体的影响,是基础题.
21.(1) (2)60人 (3)76分
【分析】
(1)利用诸矩形面积和为1可求的值.
(2)由直方图可得之间的频率,从而可估计总体中获奖的大约人数.
(3)利用组中值可得平均分的估计值.
【详解】
(1)由,解得
(2)学生成绩在之间的频率为0.05,
故可估计所有参赛学生中能获奖的人数约为人
(3)平均分的估计值为:分
【点睛】
本题考查频率分布直方图的应用,属于基础题.
22.(1)中位数为81.5,方差为98.83(2)详见解析
【分析】
(1)把样本数据排序后可得中位数,计算样本数据的平均数再利用公式计算其方差.
(2)利用超几何分布可求优秀作品的件数的分布列和期望.
【详解】
(1)样本数据按顺序为59,67,73,76,78,81,82,84,85,86,93,96.
数据的中位数为:
平均数为
方差为
(2)设抽到优秀作品的个数为,则的可能值为0,1,2,3
所以的分布列为:
0 1 2 3
期望为
【点睛】
(1)统计中有中位数、众数和平均数,注意它们的差别与计算方法.
(2)在计算离散型随机变量的概率时,注意利用常见的概率分布列来简化计算(如二项分布、超几何分布等).
一、单选题
1.医生要检验人血液中血脂的含量,采取的调查方法应该是( )
A.普查 B.抽样调查 C.既不能普查也不能抽样调查 D.普查与抽样调查都可以
2.某校高三一班有学生54人,二班有学生42人,现在要用分层随机抽样的方法从两个班抽出16人参加军训表演,则两班分别被抽取的人数是( )
A.8,8 B.10,6 C.9,7 D.12,4
3.从编号为01,02,…,49,50的50个个体中利用下面的随机数表选取5个个体,选取方法从随机数表第1行第5列的数开始由左到右依次抽取,则选出来的第5个个体的编号为( )
7816 6572 0812 1463 0782 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.14 B.07
C.32 D.43
4.2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化、国际化、便利化的营商环境,不断提高贸易便利化水平,外贸稳规模、提质量、转动力取得阶段性成效,进出口保持稳中提质的发展势头,如图是某省近五年进出口情况统计图,下列描述错误的是( )
A.这五年,2015年出口额最少 B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降 D.这五年,2019年进口增速最快
5.现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从2000名学生中抽取100名进行课后阅读情况调查;③从某社区100户高收人家庭,270户中等收人家庭,80户低收人家庭中选出45户进行消费水平调查.较为合理的抽样方法是( )
A.①系统抽样,②简单随机抽样,③分层抽样 B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样 D.①简单随机抽样,②系统抽样,③分层抽样
6.某校8位学生的本次月考成绩恰好都比上一次的月考成绩高出50分,则以该8位学生这两次的月考成绩各自组成样本,则这两个样本不变的数字特征是( )
A.方差 B.中位数 C.众数 D.平均数
7.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(如图一),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(如图二)完好,则下列结论正确的是( )
A.甲得分的极差是11 B.乙得分的中位数是18.5
C.甲有3场比赛的单场得分超过20 D.甲的单场平均得分比乙高
8.用简单随机抽样的方法从含有个个体的总体中抽取一个容量为的样本,其中某一个体“第一次被抽到”的可能性与“第二次被抽到”的可能性分别是( )
A.、 B.、
C.、 D.、
9.疫情期间,为了贯彻“停课不停学”的理念,唐老师组织学生参与了一次网络在线考试,并计算出本次考试中全体学生的平均分为85,方差为58;后来有两位学生反应,自己的成绩被登记错误,一位学生的成绩为100分,记录成80分,另一位学生的成绩为70分,记录成90分,唐老师对这两位学生的成绩进行更正后,得到的平均分为,方差为,则( )
A., B.,
C., D.,
10.已知一组数据,,,,的方差是,那么另一组数据,,,,的方差是( ).
A.1 B.2 C. D.4
11.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米2020石,验得米内夹谷,抽样取米一把,数得255粒内夹谷29粒,则这批米内夹谷约为( )
A.222石 B.220石 C.230石 D.232石
12.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为且支出在元的样本,其频率分布直方图如图所示,其中支出在元的学生有30人,则的值为( )
A.90 B.100 C.900 D.1000
二、填空题
13.某班有男生36人,女生18人,用分层抽样的方法从该班全体学生中抽取一个容量为6的样本,则抽取的女生人数为________.
14.某校有教师人,男学生人,女学生人,现用分层抽样的方法从所有师生中抽取一个容量为的样本.已知从女学生中抽取的人数为人,则的值为________.
15.“沃尔玛”商场在国庆“62”黄金周的促销活动中,对10月2日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售为5万元,则11时至12时的销售额为______万元.
16.已知甲、乙两组数据如茎叶图所示,若两组数据的中位数相同,平均数也相同,那么m+n=________.
三、解答题
17.某中学从40名学生中选1名学生作为某男篮拉拉队成员,采用下面两种方法选取.
方法一:将40名学生按1~40进行编号,相应制作1~40的40个号签,把这40个号签放在一个暗箱中搅拌均匀,最后随机地从中抽取1个号签,与这个号签号码一致的学生幸运入选;方法二;将39个白球与1个红球混合放在一个暗箱中搅匀,让40名学生逐一从中摸取l个球,摸到红球的学生成为拉拉队成员.
试问这两种方法是否都是抽签法?为什么?
18.为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:
(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中a,b的值.
19.某学校为了调查高一年级学生的体育锻炼情况,从甲、乙、丙3个班中,按分层抽样的方法获得了部分学生一周的锻炼时间?(单位:h),数据如下,
甲 6 6.5 7 7.5 8
乙 6 7 8 9 10 11 12
丙 3 4.5 6 7.5 9 10.5 12 13.5
?(1)求三个班中学生人数之比;
?(2)估计这个学校高一年级学生中,一周的锻炼时间超过10h的百分比;
?(3)估计这个学校高一年级学生一周的平均锻炼时间.
20.据报道,某公司的33名职工的月工资(以元为单位)如下:
职务 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5500 3500 3000 2500 2000 1500
(1)求该公司职工月工资的平均数(精确到元);
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数又是什么?(精确到元)
(3)你认为工资的平均数能反映这个公司员工的工资水平吗?结合此问题谈一谈你的看法.
21.我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为,,,,,其频率分布直方图如图所示,请你解答下列问题:
(1)求的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
22.2018年茂名市举办“好心杯”少年美术书法作品比赛,某赛区收到200件参赛作品,为了解作品质量,现从这些作品中随机抽取12件作品进行试评.成绩如下:67,82,78,86,96,81,73,84,76,59,85,93.
(1)求该样本的中位数和方差;
(2)若把成绩不低于85分(含85分)的作品认为为优秀作品,现在从这12件作品中任意抽取3件,求抽到优秀作品的件数的分布列和期望.
参考答案
1.B
【分析】
根据普查和抽样调查的特点进行判断即可.
【详解】
只能抽样调查,如果普查,人也活不了了,
故选:B.
【点睛】
本题考查的是调查方法的选择,正确选择调查方法要根据调查方式的优缺点再结合实际情况去分析.
2.C
【分析】
先计算每个个体被抽到的概率,再用每层的个体数乘以每个个体被抽到的概率,即得到该层应抽取的个体数.
【详解】
抽样比为,则两班分别被抽取的人数是, .
故从一班抽出9人,从二班抽出7人.
故选:C.
【点睛】
本题考查分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数.
3.D
【分析】
根据随机数表的取法,从第1行第5列的数开始两个两个的读数,不大于50的保留,大于50的去掉,保留到第5个即得.
【详解】
由题意知选定的第一个数为65(第1行的第5列和第6列),按由左到右选取两位数(大于50的跳过、重复的不选取),前5个个体编号为08,12,14,07,43.故选出来的第5个个体的编号为43.
故选:D.
【点睛】
本题考查随机数表,掌握随机数表取数规则即可.
4.C
【分析】
观察白色条形图可分析选项A,观察5组条形图可分析选项B,观察虚线折线图可分析选项C,观察实线折线图可分析选项D.
【详解】
对于选项A,观察5个白色条形图可知,这五年中2015年出口额最少,故A正确;
对于选项B,观察五组条形图可得,2015年出口额比进口额稍低,
但2016年至2019年出口额都高于进口额,并且2017年和2018年出口额都明显高于进口额,
故这五年,出口总额比进口总额多,故B正确;
对于选项C,观察虚线折线图可知,2015年到2016年出口增速是上升的,故C错误;
对于选项D,从图中可知,实线折线图2019年是最高的,即2019年进口增速最快,故D正确.
故选:C.
【点睛】
本题考查条形统计图的性质应用,考查数据分析能力,属于基础题.
5.D
【分析】
根据系统抽样、简单随机抽样、分层抽样的概念判断.
【详解】
在①中,由于总体个数较少,故采用简单随机抽样即可;
在②中,由于总体个数较多,故采用系统抽样较好;
在③中,由于高收入家庭、中等收入家庭和低收人家庭的消费水平差异明显,
故采用分层抽样较好.
故选:D.
【点睛】
本题考查抽样的概念,掌握系统抽样、简单随机抽样、分层抽样的概念是解题关键.
6.A
【分析】
通过方差公式分析可知方差没有改变,中位数、众数和平均数都发生了改变.
【详解】
由题可知,中位数和众数、平均数都有变化.
本次和上次的月考成绩相比,成绩和平均数都增加了50,所以没有改变,
根据方差公式可知方差不变.
故选:A
【点睛】
本题主要考查样本的数字特征,意在考查学生对这些知识的理解掌握水平.
7.D
【分析】
根据茎叶图,折线图整合数据,判断选项.
【详解】
甲的极差为,故A选项不符合题意.
乙的中位数为,故选项B不符合题意.
甲得分的折线图可知甲运动员得分有2次超过20,故选项C不符合题意.
根据茎叶图和折线图可知,甲的单场平均得分大于,乙的单场平均得分为,故甲的单场平均得分比乙高.
故选:D.
【点睛】
本题考查对茎叶图,折线图的分析整合能力,属于基础题.
8.A
【分析】
根据抽样中,每个个体在每一次被抽到的概率都是相等的,由此可得出结果.
【详解】
在抽样过程中,个体每一次被抽中的概率是相等的,因为总体容量为,
故个体“第一次被抽到”的可能性与“第二次被抽到”的可能性均为,
故选:A.
【点睛】
本题考查抽样中概率的计算,属于基础题.
9.A
【分析】
由于,,,再根据平均数和方差的计算公式可得选项.
【详解】
由于,因此更正前后样本的平均数不发生改变,即;
由于,,因此更正后样本的方差变大,即;故选:A.
【点睛】
本题考查平均数和方差的计算原理,属于基础题.
10.B
【分析】
根据数据关系得方差关系,即可求解.
【详解】
因为数据,,,,的方差是数据,,,,的方差的4倍,所以数据,,,,的方差是
故选:B
【点睛】
本题考查方差、新旧数据方差关系,考查基本分析求解能力,属基础题.
11.C
【分析】
根据米255粒内夹谷29粒,求得频率,再根据频率计算这批米内夹谷量.
【详解】
根据米255粒内夹谷29粒,则频率为,
则这批米内夹谷约为(石).
故选:C.
【点睛】
本题考查了用样本估计总体,属于基础题.
12.B
【分析】
先由频率分布直方图求出支出在元的频率,然后根据频率、频数和样本容量间的关系求解即可得到答案.
【详解】
由频率分布直方图可得支出在元的频率为,
因此,
解得.
故选:B.
【点睛】
频率分布直方图直观形象地表示了样本的频率分布,从这个直方图上可以求出样本数据在各个组的频率分布.本题考查识图、用图和计算能力,属于基础题.
13.2
【分析】
分层抽样的抽取比例为,抽取的女生人数为抽取比例女生人数.
【详解】
由题意知:分层抽样的抽取比例为,
抽取的女生人数为.
故答案为:2.
【点睛】
本题考查了分层抽样方法,熟练掌握分层抽样的定义是关键,属于基础题.
14.
【分析】
根据女学生的入样比与总体的入样比相等列等式可求出的值.
【详解】
由于女学生的入样比与总体的入样比相等,则,解得.
故答案为:.
【点睛】
本题考查分层抽样的定义和方法,根据每层的入样比与总体的入样比相等列等式是解答的关键,考查运算求解能力,属于基础题.
15.20
【分析】
根据频率分布直方图计算出时至时的销售额.
【详解】
由于时至时的销售额为万元,根据频率分布直方图可知时至时的销售额为万元.
故答案为:
【点睛】
本小题主要考查频率分布直方图,属于基础题.
16.11
【分析】
由两组数据平均数相同有,再由中位数相等可得,即可求n,所以的值可得
【详解】
由平均数相同知:,有
对于乙:,32,34,38,则中位数为
∵两组数据的中位数相同
∴有
即有
故有
故答案为:11
【点睛】
本题考查了利用茎叶图,结合平均数、中位数概念求参数
17.见解析
【分析】
根据抽签法的概念进行判断即可.
【详解】
解:抽签法抽样时给总体中的N个个体编号各不相同,由此可知方法一是抽签法,因为抽签法要求所有的号签编号互不相同,而方法二中39个白球无法相互区分,故方法二不是抽签法.
这两种方法的相同之处在于每名学生被选中的机会都相等.
【点睛】
本题考查抽签法的概念,是基础题.
18.(1);(2),.
【分析】
(1)由频率分布表即可得解;
(2)由频率分布直方图中小矩形的高为频率与组距的比值,观察频率分布表的数据即可得解.
【详解】
解:(1)记“从该单位随机选取一名职工,这名职工该周路边停车的时间少于8小时”为事件A,则;
(2)由频率分布表可得:区间的频数为8, 则,
区间的频数为12,则.
【点睛】
本题考查了频率分布表及频率分布直方图,属基础题.
19.(1)(2)25%(3)8.2h
【分析】
(1)样本中人数比例与总体中人数比例相等;
(2)求出样本中一周的锻炼时间超过10h的人数,求得比例,再估计年段的比例;
(3)求出样本的平均数,从而估计年段的平均数.
【详解】
(1)三个班中学生人数之比为.
(2)样本中一周的锻炼时间超过10h的有5个,
因此一周的锻炼时间超过10h的百分比为.
估计该校高一年级学生中,一周的锻炼时间超过10h的百分比为25%.
?(3)样本中甲、乙、丙三个班级的平均锻炼时间分别为7h,9h,8.25h,
则样本平均数为.
估计该校高一年级学生一周的平均锻炼时间为8.2h.
【点睛】
本题考查频率、平均数的计算,考查数据处理能力,属于基础题.
20.(1)2091元 (2)3288元 (3)不能反映这个公司员工的工资水平.见解析
【分析】
(1)根据平均数的计算公式计算即可;
(2)根据平均数的计算公式计算即可;
(3)根据某些个题对总体的影响情况来说明.
【详解】
解:(1)平均数是
(元).
(2)平均数是
(元).
(3)在这个问题中,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数偏差较大,所以平均数不能反映这个公司员工的工资水平.
【点睛】
本题考查平均数的计算,以及个体对总体的影响,是基础题.
21.(1) (2)60人 (3)76分
【分析】
(1)利用诸矩形面积和为1可求的值.
(2)由直方图可得之间的频率,从而可估计总体中获奖的大约人数.
(3)利用组中值可得平均分的估计值.
【详解】
(1)由,解得
(2)学生成绩在之间的频率为0.05,
故可估计所有参赛学生中能获奖的人数约为人
(3)平均分的估计值为:分
【点睛】
本题考查频率分布直方图的应用,属于基础题.
22.(1)中位数为81.5,方差为98.83(2)详见解析
【分析】
(1)把样本数据排序后可得中位数,计算样本数据的平均数再利用公式计算其方差.
(2)利用超几何分布可求优秀作品的件数的分布列和期望.
【详解】
(1)样本数据按顺序为59,67,73,76,78,81,82,84,85,86,93,96.
数据的中位数为:
平均数为
方差为
(2)设抽到优秀作品的个数为,则的可能值为0,1,2,3
所以的分布列为:
0 1 2 3
期望为
【点睛】
(1)统计中有中位数、众数和平均数,注意它们的差别与计算方法.
(2)在计算离散型随机变量的概率时,注意利用常见的概率分布列来简化计算(如二项分布、超几何分布等).
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
