第9章统计 单元综合检测题-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课前检测(Word版含解析)
文档属性
| 名称 | 第9章统计 单元综合检测题-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课前检测(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 795.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览




文档简介
人教A版第九章统计单元综合检测题
一、单选题
1.下列抽样试验中,适合采用抽签法的是( )
A.从某厂生产的5000件产品中抽取600件进行质量检验
B.从某厂生产的两箱产品(每箱18件)中抽取6件进行质量检验
C.从甲、乙两厂生产的两箱产品(两厂各一箱,每箱18件)中抽取6件进行质量检验
D.从某厂生产的5000件产品中抽取10件进行质量检验
2.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图甲和乙所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
A.160,12 B.120,12 C.160,9 D.120,9
3.电视台某节目组要从名观众中抽取名幸运观众.先用简单随机抽样从人中剔除人,剩下的人再按系统抽样方法抽取人,则在人中,每个人被抽取的可能性( )
A.都相等,且为 B.都相等,且为
C.均不相等 D.不全相等
4.甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 参赛人数 平均数 中位数 众数 方差
甲 45 83 86 85 82
乙 45 83 84 85 133
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
5.现要完成下列三项抽样调查:①从罐奶粉中抽取罐进行食品安全卫生检查;②高二年级有名学生,为调查学生的学习情况抽取一个容量为的样本;③从某社区户高收入家庭,户中等收入家庭,户低收入家庭中选出户进行消费水平调查.以下各调查方法较为合理的是( )
A.①系统抽样,②简单随机抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样
D.①简单随机抽样,②系统抽样,③分层抽样
6.在某次测量中得到的样本数据如下17,22,37,42,31,58,61,若B样本数据恰好是样本数据都减2后所得数据,则,两样本的下列数字特征对应相同的是( )
A.平均数 B.众数 C.中位数 D.方差
7.设样本数据,,,…,,的均值和方差分别为和,若 (),则,,,…,,的均值和方差分别为( )
A., B., C., D.,
8.已知样本数据为,该样本平均数为2021,方差为1,现加入一个数2021,得到新样本的平均数为,方差为,则( )
A. B. C. D.
9.某中学初中部有600名学生,高中部有800名学生,其性别比例如图所示,则该校男生比女生多( )
A.60人 B.100人 C.150人 D.180人
10.如图所示的茎叶图记录了甲?乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为106,乙组数据的平均数为,则x,y的值分别为( )
A.5,7 B.6,8 C.6,9 D.8,8
11.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,后从事互联网行业岗位分布条形图,则下列结论错误的是( )
注:后指年及以后出生,后指年之间出生,前指年及以前出生.
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的
C.互联网行业中从事运营岗位的人数后一定比前多
D.互联网行业中从事技术岗位的人数后一定比后多
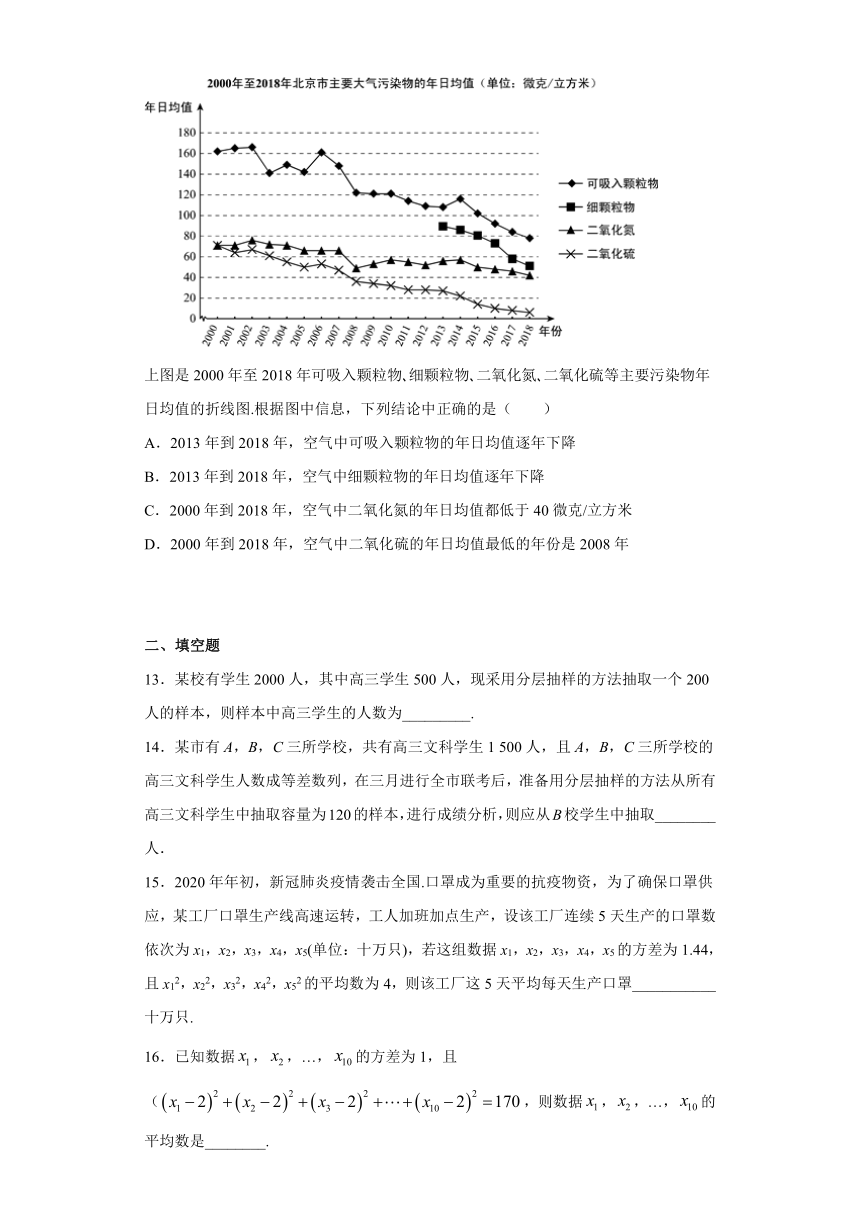
12.年以前,北京市先后组织实施了多个阶段的大气污染防治行动,针对燃煤?工业?扬尘排放和机动车排放等采取了数百项治理措施.2008年北京市首次探索区域联防联控,取得了良好效果.2013年北京市制定实施以防治细颗粒物为重点的《2013-2017年清洁空气行动计划》,治理成效显著.
上图是2000年至2018年可吸入颗粒物?细颗粒物?二氧化氮?二氧化硫等主要污染物年日均值的折线图.根据图中信息,下列结论中正确的是( )
A.2013年到2018年,空气中可吸入颗粒物的年日均值逐年下降
B.2013年到2018年,空气中细颗粒物的年日均值逐年下降
C.2000年到2018年,空气中二氧化氮的年日均值都低于40微克/立方米
D.2000年到2018年,空气中二氧化硫的年日均值最低的年份是2008年
二、填空题
13.某校有学生2000人,其中高三学生500人,现采用分层抽样的方法抽取一个200人的样本,则样本中高三学生的人数为_________.
14.某市有A,B,C三所学校,共有高三文科学生1 500人,且A,B,C三所学校的高三文科学生人数成等差数列,在三月进行全市联考后,准备用分层抽样的方法从所有高三文科学生中抽取容量为120的样本,进行成绩分析,则应从B校学生中抽取________人.
15.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产,设该工厂连续5天生产的口罩数依次为x1,x2,x3,x4,x5(单位:十万只),若这组数据x1,x2,x3,x4,x5的方差为1.44,且x12,x22,x32,x42,x52的平均数为4,则该工厂这5天平均每天生产口罩___________十万只.
16.已知数据,,…,的方差为1,且(,则数据,,…,的平均数是________.
三、解答题
17.实验室的笼子里共有100只小白鼠,现要从中抽取10只作试验用.下列两种情况是否属于简单随机抽样?请说明理由.
(1)每次不经任何挑选地抓一只,抓满10只为止;
(2)将笼中的100只小白鼠按1~100编号,任意选出编号范围内的10个不重复数字,把相应编号的小白鼠作为试验用的小白鼠.
18.某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数;
(3)求这次测试数学成绩的平均分.
19.从甲乙两种棉花苗中各抽10株,测得它们的株高分别如下(单位:cm)
甲:25,41,40,37,22,14,19,39,21,42
乙:27,16,44,27,44,16,40,40,16,40
(1)估计两种棉花苗总体的长势,哪种长的高一些?
(2)哪种棉花的苗长得整齐一些?
20.某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为一、二、三、四,四个等级,加工业务约定:对于一级品、二级品、三级品,厂家每件分别收取加工费9元,5元,2元;对于四级品,厂家每件要赔偿原料损失费5元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为2.5元/件,乙分厂加工成本费为2元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 一 二 三 四
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 一 二 三 四
频数 20 55 15 10
(1)分别估计甲、乙两分厂加工出来的一件产品为一级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
21.某市模拟考试,共有15000名学生参加考试,随机抽取100名学生,将其成绩分为六段,,,,,,得到如图所示的频率分布直方图.
(1)求图中a的值并利用样本估计全市分数在之间的人数;
(2)利用样本估计该次考试的全市平均分.(每组数据用该组的区间中点值表示).
22.甲、乙两位学生参加数学文化知识竞赛培训.在培训期间,他们参加的5次测试成绩记录如下:
甲 82 82 79 95 87
乙 95 75 80 90 85
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)现要从甲、乙两位同学中选派一人参加正式比赛,从统计学的角度考虑,你认为选派哪位同学参加合适?并说明理由.
参考答案
1.B
【分析】
根据抽签法适用的条件以及实施方法,可判断结论
【详解】
显然,A,D选项是简单随机抽样,但总体中的个体数太多,
不宜采用抽签法.
C选项中两箱产品来自两个不同的工厂,甲厂生产的产品不能代表乙厂,
乙厂生产的产品也不能代表甲厂,所以不宜采用抽签法.
故选B.
【点睛】
本题考查简单随机抽样的方法,属于基础题.
2.A
【分析】
根据甲图可得样本容量,再根据乙图计算对四居室满意的人数.
【详解】
样本的容量,
抽取的户主对四居室满意的人数为,
故选:A.
【点睛】
本题考查统计图表的识别,属基础题.
3.A
【分析】
根据随机抽样等可能抽取的性质即可求解.
【详解】
由随机抽样等可能抽取,可知每个个体被抽取的可能性相等,
故抽取的概率为.
故选:A
【点睛】
本题考查了随机抽样的特点,属于基础题.
4.C
【分析】
①看两班的平均数易知正确;②看两班的中位数正确;③看两班的众数正确;④看两班的方差.
【详解】
①从表看出甲、乙两班学生的平均成绩相同,正确;
②因为乙班的中位数比甲班的小,所以正确;
③根据甲、乙两班的众数,所以正确;
④因为乙班的方差比甲的大,所以波动比甲班大,所以错误
故选:C.
【点睛】
本题主要考查了样本中的数字特征,还考查了理解辨析的能力,属于基础题.
5.D
【分析】
根据简单随机抽样、系统抽样及分层抽样的概念及适用情况,直接判断求解即可.
【详解】
对于① ,从罐奶粉中抽取罐进行食品安全卫生检查,由于总体数量较少,因此可用简单随机抽样的方法调查.
对于② ,高二年级有名学生,为调查学生的学习情况抽取一个容量为的样本.总体数量较多,且对于学生来说,有可以直接使用的学号等编码,所以选择系统抽样调查.
对于③ ,从某社区户高收入家庭,户中等收入家庭,户低收入家庭中选出户进行消费水平调查.调查的各个家庭收入有差距,因而选择分层抽样调查的方法.
综上可知,对三项分别使用的调查方法为: 简单随机抽样; 择系统抽样; 分层抽样.
故选:D
【点睛】
本题考查了抽样方法的判断和选择,对抽样方法适用条件的判断,属于基础题.
6.D
【分析】
B样本数据是样本数据都减2后所得的,则A、B两样本数据的平均数、众数、中位数都发生改变,由方差的统计学意义可知, A、B的方差不变.
【详解】
由数据A : 17,22,37,42,31,58,61得到数据B: 15,20,35,40,29,56,59,
所以B的平均数、众数、中位数比A的平均数、众数、中位数均小2;
因为A、B的离散程度相同, 所以A、B的方差相同.
故选:D
【点睛】
(1) 平均数:是指在一组数据中所有数据之和再除以这组数据的个数,表示一组数据集中趋势的量数;
(2) 方差:是各个数据分别与其平均数之差的平方的和的平均数,数据和其数学期望(即均值)之间的偏离程度,反映数据离散程度.两组数据的离散程度相同, 所以他们的方差相同.
7.D
【分析】
设样本数据的均值为,方差为,由已知得新样本的均值为,方差为,可得选项.
【详解】
设样本数据的均值为,则,方差为,则,所以新样本的均值为,方差为.
故选:D.
8.B
【分析】
根据题目计算新的数据的和,进而计算出平均数,再结合方差计算公式计算方差即可.
【详解】
由题知,
,
所以
,
所以.
故选:B
9.B
【分析】
分别求出初中部男生人数和女生人数,高中部女生人数和男生人数,由此能求出该校男生比女生多多少人.
【详解】
解:由题意可得,初中部男生人数为,女生人数为;高中部女生人数为,男生人数为.故该校男生比女生多人.
故选:B
10.B
【分析】
根据茎叶图中的数据,结合中位数与平均数的概念,即可求出、的值.
【详解】
∵甲组数据的中位数为106
∴
又∵乙组数据的平均数为
∴
解得
综上,x,y的值分别为6,8
故选:B
11.D
【分析】
根据整个互联网行业从业者年龄分布饼状图、后从事互联网行业岗位分布条形图,对四个选项逐一分析,即可得出正确选项.
【详解】
对于选项A,因为互联网行业从业人员中,“后”占比为,
其中从事技术和运营岗位的人数占的比分别为和,
则“后”从事技术和运营岗位的人数占总人数的.
“前”和“后”中必然也有从事技术和运营岗位的人,则总的占比一定超过三成,
故选项A正确;
对于选项B,因为互联网行业从业人员中,“后”占比为,
其中从事技术岗位的人数占的比为,
则“后”从事技术岗位的人数占总人数的.
“前”和“后”中必然也有从事技术岗位的人,则总的占比一定超过,故选项B正确;
对于选项C,“后”从事运营岗位的人数占总人数的比为,
大于“前”的总人数所占比,故选项C正确;
选项D,“后”从事技术岗位的人数占总人数的,
“后”的总人数所占比为,条件中未给出从事技术岗位的占比,故不能判断,所以选项D错误.
故选:D.
【点睛】
关键点点睛:本题考查利用扇形统计图和条形统计图解决实际问题,解本题的关键就是利用条形统计图中“后”事互联网行业岗位的占比乘以“后”所占总人数的占比,再对各选项逐一分析即可.
12.B
【分析】
观察折线图,确定数据的变化规律,判断各选项.
【详解】
2014年空气中可吸入颗粒物年日均值比2013年多,A错;
2013年到2018年,空气中细颗粒物的年日均值逐年下降,B正确;
2007年(含2007年)之前空气中二氧化氮的年日均值都高于40微克/立方米,C错;
2000年到2018年,空气中二氧化硫的年日均值最低的年份是2018年,D错.
故选:B.
13.50
【分析】
根据每层抽取样本的比例与抽取总样本的比例相等求解即可.
【详解】
分层抽样即是按比例抽样,
易知抽样比例为,
故500名高三学生应抽取的人数为人.
故答案为:50
【点睛】
本题是分层抽样的相关知识.容易出错的是不理解分层抽样的含义或与其它混淆.抽样方法是数学中的一个小知识点,但一般不难,故也是一个重要的得分点,不容错过.
14.40
【分析】
利用等差中项可得B校学生总人数为500,再利用分层抽样比即可求解.
【详解】
设A,B,C三所学校高三文科学生人数分别为x,y,z,
由题知x,y,z成等差数列,
所以x+z=2y,又x+y+z=1 500,
所以y=500,用分层抽样方法抽取B校学生人数为×500=40(人).
故答案为:40
15.1.6
【分析】
由题意结合平均数,方差的定义整理计算即可求得最终结果.
【详解】
设该工厂这5天平均每天生产口罩为,
由题意可得,
则,
由,
可得,
解得.
故答案为:1.6
16.或6.
【分析】
由数据,,…,的方差为1,且,把所给的式子进行整理,两式相减,得到关于数据的平均数的一元二次方程,解方程即可.
【详解】
数据,,…,的方差为1,
,
,
,①
,
,
,②
将②-①得,解得,或,
故答案为:或6.
【点睛】
本题主要考查一组数据的平均数的求法,解题时要熟练掌握方差的计算公式的灵活运用,属于中档题.
17.(1)属于简单随机抽样;(2)属于简单随机抽样. 理由:(1)(2)都满足简单随机抽样的四个特征:①有限性;②逐个抽取;③不放回;④等可能性.
【分析】
根据简单随机抽样的四个特征:①有限性;②逐个抽取;③不放回;④等可能性,进行判断.
【详解】
(1)属于简单随机抽样;(2)属于简单随机抽样.
理由:(1)(2)都满足简单随机抽样的四个特征:①有限性;②逐个抽取;③不放回;④等可能性.
【点睛】
本题考查简单随机抽样的特征,是基础题.
18.(1);(2);(3).
【分析】
(1)取频率分布直方图中最高矩形的分数中点值即可得答案;
(2)根据中位数将频率分布直方图两边的面积平分计算即可;
(3)用每组中点值乘以该组的频率求和即可得答案.
【详解】
(1)因为频率分布直方图中最高矩形在之间,故众数为;
(2)根据题意得:第一组的频率为,第二组的频率为,
第三组的频率为,第四组的频率为,由于前三组的频率和为,
所以中位数为:;
(3)根据题意,平均数为:
.
19.(1)乙棉花长的更高;(2)甲棉花长的更整齐
【分析】
(1)分别求出甲乙两种棉花株高的平均数,比较二者大小,可得出结论;
(2)分别求出方差,比较二者大小,方差小的,长的更整齐.
【详解】
(1)甲的平均株高为:
,
乙的平均株高为:
,
因为,所以乙棉花长的更高.
(2)甲的方差为:
,
乙的方差为:
,
因为,所以甲棉花株高较平稳,即甲种棉花长的更整齐.
【点睛】
本题考查平均数、方差的求法及应用,考查学生的计算求解能力,属于基础题.
20.(1),;(2)甲的平均利润为元/件;乙的平均利润为元/件;应该选择乙厂承接加工业务.
【分析】
(1)根据频率频数÷样本容量可得结果;
(2)利用频率乘以每件产品的利润,再相加可得平均利润,比较平均利润的大小可得结论.
【详解】
(1)甲分厂加工出来的一件产品为一级品的概率为,乙分厂加工出来的一件产品为一级品的概率为.
(2)甲分厂加工出来的100件产品的平均利润为元/件,
乙分厂加工出来的100件产品的平均利润为元/件,
因为,所以应该选择乙分厂承接加工业务.
【点睛】
本题考查了频数分布表,考查了利用频数分布表计算频率和平均值,属于基础题.
21.(1),人数为人;(2).
【分析】
(1)根据6个矩形的面积和为1列式可求出,再根据频数样本容量×频率可求出全市分数在之间的人数;
(2)用每个区间的中点值乘以相应区间的频率再相加可得结果.
【详解】
(1),
全市分数在之间的人数人.
(2)设全市平均分为,
则.
【点睛】
关键点点睛:掌握用频率分布直方图求平均数的方法是解题关键.
22.(1);(2)派甲参赛比较合适;答案见解析.
【分析】
(1)甲被抽到的成绩为x,乙被抽到成绩为y,用数对表示基本事件,可列举出所有基本事件,也可得出符合的基本事件,计数后可计算概率;
(2)计算两者的均值和方差后比较可得.
【详解】
解(1)记甲被抽到的成绩为x,乙被抽到成绩为y,用数对表示基本事件:
,
,
,
,
,
样本空间中样本点共25个,且每个样本点发生的可能性相同.
设“甲的成绩比乙高”为事件A,事件A包含的样本点:
,
,
事件A包含的基本事件数.所以,.
(2)派甲参赛比较合适,理由如下:
甲
乙
甲
乙
因为甲=乙,甲乙,
所以,甲的成绩较稳定,派甲参赛比较合适.
【点睛】
思路点睛:本题考查古典概型,考查均值与方差的计算.解题时以甲乙两人的成绩组成数对为一个基本事件,这样可用列举法列出两人成绩各随机抽取一个的所有基本事件,同时得出满足题意的基本事件,从而可计算出概率.成绩的优劣问题通常先考虑均值,在均值相等的情况下考虑方差,方差反应稳定状况.
一、单选题
1.下列抽样试验中,适合采用抽签法的是( )
A.从某厂生产的5000件产品中抽取600件进行质量检验
B.从某厂生产的两箱产品(每箱18件)中抽取6件进行质量检验
C.从甲、乙两厂生产的两箱产品(两厂各一箱,每箱18件)中抽取6件进行质量检验
D.从某厂生产的5000件产品中抽取10件进行质量检验
2.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图甲和乙所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
A.160,12 B.120,12 C.160,9 D.120,9
3.电视台某节目组要从名观众中抽取名幸运观众.先用简单随机抽样从人中剔除人,剩下的人再按系统抽样方法抽取人,则在人中,每个人被抽取的可能性( )
A.都相等,且为 B.都相等,且为
C.均不相等 D.不全相等
4.甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 参赛人数 平均数 中位数 众数 方差
甲 45 83 86 85 82
乙 45 83 84 85 133
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
5.现要完成下列三项抽样调查:①从罐奶粉中抽取罐进行食品安全卫生检查;②高二年级有名学生,为调查学生的学习情况抽取一个容量为的样本;③从某社区户高收入家庭,户中等收入家庭,户低收入家庭中选出户进行消费水平调查.以下各调查方法较为合理的是( )
A.①系统抽样,②简单随机抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样
D.①简单随机抽样,②系统抽样,③分层抽样
6.在某次测量中得到的样本数据如下17,22,37,42,31,58,61,若B样本数据恰好是样本数据都减2后所得数据,则,两样本的下列数字特征对应相同的是( )
A.平均数 B.众数 C.中位数 D.方差
7.设样本数据,,,…,,的均值和方差分别为和,若 (),则,,,…,,的均值和方差分别为( )
A., B., C., D.,
8.已知样本数据为,该样本平均数为2021,方差为1,现加入一个数2021,得到新样本的平均数为,方差为,则( )
A. B. C. D.
9.某中学初中部有600名学生,高中部有800名学生,其性别比例如图所示,则该校男生比女生多( )
A.60人 B.100人 C.150人 D.180人
10.如图所示的茎叶图记录了甲?乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为106,乙组数据的平均数为,则x,y的值分别为( )
A.5,7 B.6,8 C.6,9 D.8,8
11.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,后从事互联网行业岗位分布条形图,则下列结论错误的是( )
注:后指年及以后出生,后指年之间出生,前指年及以前出生.
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的
C.互联网行业中从事运营岗位的人数后一定比前多
D.互联网行业中从事技术岗位的人数后一定比后多
12.年以前,北京市先后组织实施了多个阶段的大气污染防治行动,针对燃煤?工业?扬尘排放和机动车排放等采取了数百项治理措施.2008年北京市首次探索区域联防联控,取得了良好效果.2013年北京市制定实施以防治细颗粒物为重点的《2013-2017年清洁空气行动计划》,治理成效显著.
上图是2000年至2018年可吸入颗粒物?细颗粒物?二氧化氮?二氧化硫等主要污染物年日均值的折线图.根据图中信息,下列结论中正确的是( )
A.2013年到2018年,空气中可吸入颗粒物的年日均值逐年下降
B.2013年到2018年,空气中细颗粒物的年日均值逐年下降
C.2000年到2018年,空气中二氧化氮的年日均值都低于40微克/立方米
D.2000年到2018年,空气中二氧化硫的年日均值最低的年份是2008年
二、填空题
13.某校有学生2000人,其中高三学生500人,现采用分层抽样的方法抽取一个200人的样本,则样本中高三学生的人数为_________.
14.某市有A,B,C三所学校,共有高三文科学生1 500人,且A,B,C三所学校的高三文科学生人数成等差数列,在三月进行全市联考后,准备用分层抽样的方法从所有高三文科学生中抽取容量为120的样本,进行成绩分析,则应从B校学生中抽取________人.
15.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产,设该工厂连续5天生产的口罩数依次为x1,x2,x3,x4,x5(单位:十万只),若这组数据x1,x2,x3,x4,x5的方差为1.44,且x12,x22,x32,x42,x52的平均数为4,则该工厂这5天平均每天生产口罩___________十万只.
16.已知数据,,…,的方差为1,且(,则数据,,…,的平均数是________.
三、解答题
17.实验室的笼子里共有100只小白鼠,现要从中抽取10只作试验用.下列两种情况是否属于简单随机抽样?请说明理由.
(1)每次不经任何挑选地抓一只,抓满10只为止;
(2)将笼中的100只小白鼠按1~100编号,任意选出编号范围内的10个不重复数字,把相应编号的小白鼠作为试验用的小白鼠.
18.某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数;
(3)求这次测试数学成绩的平均分.
19.从甲乙两种棉花苗中各抽10株,测得它们的株高分别如下(单位:cm)
甲:25,41,40,37,22,14,19,39,21,42
乙:27,16,44,27,44,16,40,40,16,40
(1)估计两种棉花苗总体的长势,哪种长的高一些?
(2)哪种棉花的苗长得整齐一些?
20.某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为一、二、三、四,四个等级,加工业务约定:对于一级品、二级品、三级品,厂家每件分别收取加工费9元,5元,2元;对于四级品,厂家每件要赔偿原料损失费5元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为2.5元/件,乙分厂加工成本费为2元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 一 二 三 四
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 一 二 三 四
频数 20 55 15 10
(1)分别估计甲、乙两分厂加工出来的一件产品为一级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
21.某市模拟考试,共有15000名学生参加考试,随机抽取100名学生,将其成绩分为六段,,,,,,得到如图所示的频率分布直方图.
(1)求图中a的值并利用样本估计全市分数在之间的人数;
(2)利用样本估计该次考试的全市平均分.(每组数据用该组的区间中点值表示).
22.甲、乙两位学生参加数学文化知识竞赛培训.在培训期间,他们参加的5次测试成绩记录如下:
甲 82 82 79 95 87
乙 95 75 80 90 85
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)现要从甲、乙两位同学中选派一人参加正式比赛,从统计学的角度考虑,你认为选派哪位同学参加合适?并说明理由.
参考答案
1.B
【分析】
根据抽签法适用的条件以及实施方法,可判断结论
【详解】
显然,A,D选项是简单随机抽样,但总体中的个体数太多,
不宜采用抽签法.
C选项中两箱产品来自两个不同的工厂,甲厂生产的产品不能代表乙厂,
乙厂生产的产品也不能代表甲厂,所以不宜采用抽签法.
故选B.
【点睛】
本题考查简单随机抽样的方法,属于基础题.
2.A
【分析】
根据甲图可得样本容量,再根据乙图计算对四居室满意的人数.
【详解】
样本的容量,
抽取的户主对四居室满意的人数为,
故选:A.
【点睛】
本题考查统计图表的识别,属基础题.
3.A
【分析】
根据随机抽样等可能抽取的性质即可求解.
【详解】
由随机抽样等可能抽取,可知每个个体被抽取的可能性相等,
故抽取的概率为.
故选:A
【点睛】
本题考查了随机抽样的特点,属于基础题.
4.C
【分析】
①看两班的平均数易知正确;②看两班的中位数正确;③看两班的众数正确;④看两班的方差.
【详解】
①从表看出甲、乙两班学生的平均成绩相同,正确;
②因为乙班的中位数比甲班的小,所以正确;
③根据甲、乙两班的众数,所以正确;
④因为乙班的方差比甲的大,所以波动比甲班大,所以错误
故选:C.
【点睛】
本题主要考查了样本中的数字特征,还考查了理解辨析的能力,属于基础题.
5.D
【分析】
根据简单随机抽样、系统抽样及分层抽样的概念及适用情况,直接判断求解即可.
【详解】
对于① ,从罐奶粉中抽取罐进行食品安全卫生检查,由于总体数量较少,因此可用简单随机抽样的方法调查.
对于② ,高二年级有名学生,为调查学生的学习情况抽取一个容量为的样本.总体数量较多,且对于学生来说,有可以直接使用的学号等编码,所以选择系统抽样调查.
对于③ ,从某社区户高收入家庭,户中等收入家庭,户低收入家庭中选出户进行消费水平调查.调查的各个家庭收入有差距,因而选择分层抽样调查的方法.
综上可知,对三项分别使用的调查方法为: 简单随机抽样; 择系统抽样; 分层抽样.
故选:D
【点睛】
本题考查了抽样方法的判断和选择,对抽样方法适用条件的判断,属于基础题.
6.D
【分析】
B样本数据是样本数据都减2后所得的,则A、B两样本数据的平均数、众数、中位数都发生改变,由方差的统计学意义可知, A、B的方差不变.
【详解】
由数据A : 17,22,37,42,31,58,61得到数据B: 15,20,35,40,29,56,59,
所以B的平均数、众数、中位数比A的平均数、众数、中位数均小2;
因为A、B的离散程度相同, 所以A、B的方差相同.
故选:D
【点睛】
(1) 平均数:是指在一组数据中所有数据之和再除以这组数据的个数,表示一组数据集中趋势的量数;
(2) 方差:是各个数据分别与其平均数之差的平方的和的平均数,数据和其数学期望(即均值)之间的偏离程度,反映数据离散程度.两组数据的离散程度相同, 所以他们的方差相同.
7.D
【分析】
设样本数据的均值为,方差为,由已知得新样本的均值为,方差为,可得选项.
【详解】
设样本数据的均值为,则,方差为,则,所以新样本的均值为,方差为.
故选:D.
8.B
【分析】
根据题目计算新的数据的和,进而计算出平均数,再结合方差计算公式计算方差即可.
【详解】
由题知,
,
所以
,
所以.
故选:B
9.B
【分析】
分别求出初中部男生人数和女生人数,高中部女生人数和男生人数,由此能求出该校男生比女生多多少人.
【详解】
解:由题意可得,初中部男生人数为,女生人数为;高中部女生人数为,男生人数为.故该校男生比女生多人.
故选:B
10.B
【分析】
根据茎叶图中的数据,结合中位数与平均数的概念,即可求出、的值.
【详解】
∵甲组数据的中位数为106
∴
又∵乙组数据的平均数为
∴
解得
综上,x,y的值分别为6,8
故选:B
11.D
【分析】
根据整个互联网行业从业者年龄分布饼状图、后从事互联网行业岗位分布条形图,对四个选项逐一分析,即可得出正确选项.
【详解】
对于选项A,因为互联网行业从业人员中,“后”占比为,
其中从事技术和运营岗位的人数占的比分别为和,
则“后”从事技术和运营岗位的人数占总人数的.
“前”和“后”中必然也有从事技术和运营岗位的人,则总的占比一定超过三成,
故选项A正确;
对于选项B,因为互联网行业从业人员中,“后”占比为,
其中从事技术岗位的人数占的比为,
则“后”从事技术岗位的人数占总人数的.
“前”和“后”中必然也有从事技术岗位的人,则总的占比一定超过,故选项B正确;
对于选项C,“后”从事运营岗位的人数占总人数的比为,
大于“前”的总人数所占比,故选项C正确;
选项D,“后”从事技术岗位的人数占总人数的,
“后”的总人数所占比为,条件中未给出从事技术岗位的占比,故不能判断,所以选项D错误.
故选:D.
【点睛】
关键点点睛:本题考查利用扇形统计图和条形统计图解决实际问题,解本题的关键就是利用条形统计图中“后”事互联网行业岗位的占比乘以“后”所占总人数的占比,再对各选项逐一分析即可.
12.B
【分析】
观察折线图,确定数据的变化规律,判断各选项.
【详解】
2014年空气中可吸入颗粒物年日均值比2013年多,A错;
2013年到2018年,空气中细颗粒物的年日均值逐年下降,B正确;
2007年(含2007年)之前空气中二氧化氮的年日均值都高于40微克/立方米,C错;
2000年到2018年,空气中二氧化硫的年日均值最低的年份是2018年,D错.
故选:B.
13.50
【分析】
根据每层抽取样本的比例与抽取总样本的比例相等求解即可.
【详解】
分层抽样即是按比例抽样,
易知抽样比例为,
故500名高三学生应抽取的人数为人.
故答案为:50
【点睛】
本题是分层抽样的相关知识.容易出错的是不理解分层抽样的含义或与其它混淆.抽样方法是数学中的一个小知识点,但一般不难,故也是一个重要的得分点,不容错过.
14.40
【分析】
利用等差中项可得B校学生总人数为500,再利用分层抽样比即可求解.
【详解】
设A,B,C三所学校高三文科学生人数分别为x,y,z,
由题知x,y,z成等差数列,
所以x+z=2y,又x+y+z=1 500,
所以y=500,用分层抽样方法抽取B校学生人数为×500=40(人).
故答案为:40
15.1.6
【分析】
由题意结合平均数,方差的定义整理计算即可求得最终结果.
【详解】
设该工厂这5天平均每天生产口罩为,
由题意可得,
则,
由,
可得,
解得.
故答案为:1.6
16.或6.
【分析】
由数据,,…,的方差为1,且,把所给的式子进行整理,两式相减,得到关于数据的平均数的一元二次方程,解方程即可.
【详解】
数据,,…,的方差为1,
,
,
,①
,
,
,②
将②-①得,解得,或,
故答案为:或6.
【点睛】
本题主要考查一组数据的平均数的求法,解题时要熟练掌握方差的计算公式的灵活运用,属于中档题.
17.(1)属于简单随机抽样;(2)属于简单随机抽样. 理由:(1)(2)都满足简单随机抽样的四个特征:①有限性;②逐个抽取;③不放回;④等可能性.
【分析】
根据简单随机抽样的四个特征:①有限性;②逐个抽取;③不放回;④等可能性,进行判断.
【详解】
(1)属于简单随机抽样;(2)属于简单随机抽样.
理由:(1)(2)都满足简单随机抽样的四个特征:①有限性;②逐个抽取;③不放回;④等可能性.
【点睛】
本题考查简单随机抽样的特征,是基础题.
18.(1);(2);(3).
【分析】
(1)取频率分布直方图中最高矩形的分数中点值即可得答案;
(2)根据中位数将频率分布直方图两边的面积平分计算即可;
(3)用每组中点值乘以该组的频率求和即可得答案.
【详解】
(1)因为频率分布直方图中最高矩形在之间,故众数为;
(2)根据题意得:第一组的频率为,第二组的频率为,
第三组的频率为,第四组的频率为,由于前三组的频率和为,
所以中位数为:;
(3)根据题意,平均数为:
.
19.(1)乙棉花长的更高;(2)甲棉花长的更整齐
【分析】
(1)分别求出甲乙两种棉花株高的平均数,比较二者大小,可得出结论;
(2)分别求出方差,比较二者大小,方差小的,长的更整齐.
【详解】
(1)甲的平均株高为:
,
乙的平均株高为:
,
因为,所以乙棉花长的更高.
(2)甲的方差为:
,
乙的方差为:
,
因为,所以甲棉花株高较平稳,即甲种棉花长的更整齐.
【点睛】
本题考查平均数、方差的求法及应用,考查学生的计算求解能力,属于基础题.
20.(1),;(2)甲的平均利润为元/件;乙的平均利润为元/件;应该选择乙厂承接加工业务.
【分析】
(1)根据频率频数÷样本容量可得结果;
(2)利用频率乘以每件产品的利润,再相加可得平均利润,比较平均利润的大小可得结论.
【详解】
(1)甲分厂加工出来的一件产品为一级品的概率为,乙分厂加工出来的一件产品为一级品的概率为.
(2)甲分厂加工出来的100件产品的平均利润为元/件,
乙分厂加工出来的100件产品的平均利润为元/件,
因为,所以应该选择乙分厂承接加工业务.
【点睛】
本题考查了频数分布表,考查了利用频数分布表计算频率和平均值,属于基础题.
21.(1),人数为人;(2).
【分析】
(1)根据6个矩形的面积和为1列式可求出,再根据频数样本容量×频率可求出全市分数在之间的人数;
(2)用每个区间的中点值乘以相应区间的频率再相加可得结果.
【详解】
(1),
全市分数在之间的人数人.
(2)设全市平均分为,
则.
【点睛】
关键点点睛:掌握用频率分布直方图求平均数的方法是解题关键.
22.(1);(2)派甲参赛比较合适;答案见解析.
【分析】
(1)甲被抽到的成绩为x,乙被抽到成绩为y,用数对表示基本事件,可列举出所有基本事件,也可得出符合的基本事件,计数后可计算概率;
(2)计算两者的均值和方差后比较可得.
【详解】
解(1)记甲被抽到的成绩为x,乙被抽到成绩为y,用数对表示基本事件:
,
,
,
,
,
样本空间中样本点共25个,且每个样本点发生的可能性相同.
设“甲的成绩比乙高”为事件A,事件A包含的样本点:
,
,
事件A包含的基本事件数.所以,.
(2)派甲参赛比较合适,理由如下:
甲
乙
甲
乙
因为甲=乙,甲乙,
所以,甲的成绩较稳定,派甲参赛比较合适.
【点睛】
思路点睛:本题考查古典概型,考查均值与方差的计算.解题时以甲乙两人的成绩组成数对为一个基本事件,这样可用列举法列出两人成绩各随机抽取一个的所有基本事件,同时得出满足题意的基本事件,从而可计算出概率.成绩的优劣问题通常先考虑均值,在均值相等的情况下考虑方差,方差反应稳定状况.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
