湘教版八年级上数学2.1.2三角形中的主要线段 课件(48张PPT)
文档属性
| 名称 | 湘教版八年级上数学2.1.2三角形中的主要线段 课件(48张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 14:03:18 | ||
图片预览







文档简介
(共48张PPT)
第1节
三角形
第2课时
三角形中的主要线段
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的高
三角形的角平分线
三角形的中线
课时导入
复习提问
引出问题
复习提问
引出问题
有一天,小明回家看到弟弟正在对着下边的三角形发呆,小明有一点奇怪了,外号“坐不住”的弟弟怎么能坐住了?原来是弟弟想作出三角形ABC的三条高,但是他不会作边AB、BC上的高,小明不假思索
的说:“我来帮你”,当他准备作时,也
难住了,聪明的你,能帮帮小明兄弟吗?
知识点
三角形的高
知1-导
感悟新知
1
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线(alitude),简称三角形的高.如图,AH⊥BC,垂足为点H,则线段AH
△ABC的BC边上的高.
知1-导
感悟新知
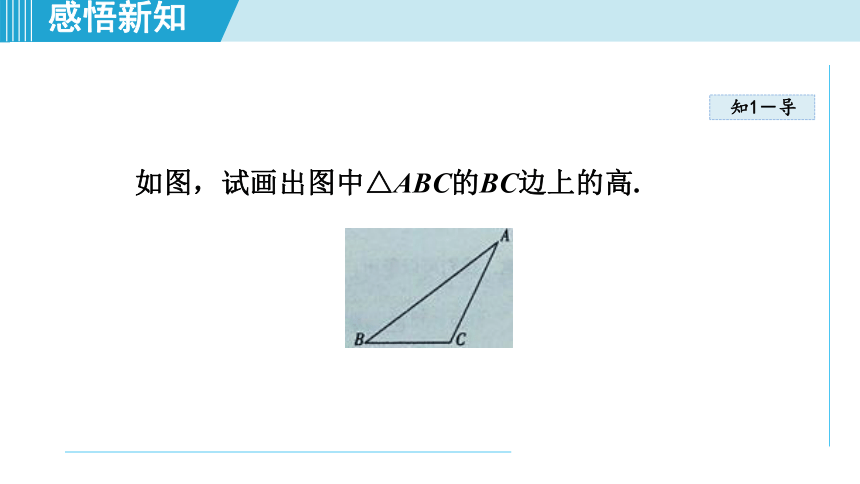
如图,试画出图中△ABC的BC边上的高.
知1-讲
感悟新知
1.定义:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做该三角形这条边上的高.一个三角形有三条高.
2.位置图例:
(1)锐角三角形:三条高都在三角形内部,
其交点也在三角形内部.
知1-讲
感悟新知
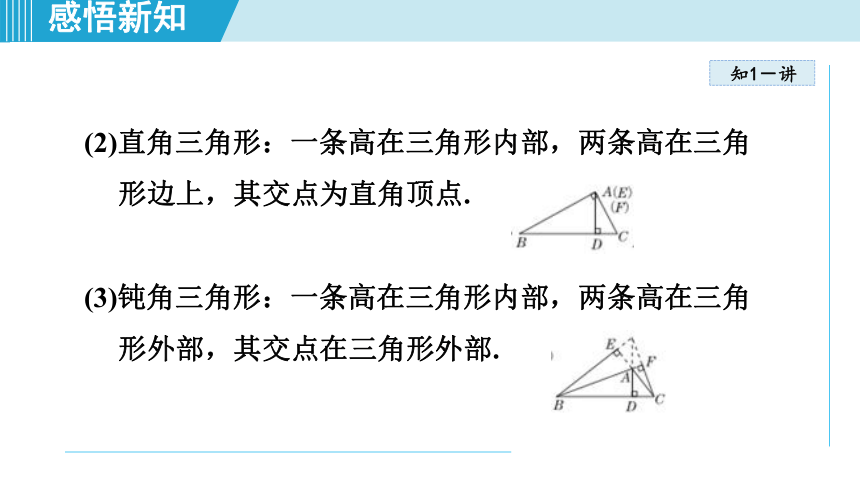
(2)直角三角形:一条高在三角形内部,两条高在三角形边上,其交点为直角顶点.
(3)钝角三角形:一条高在三角形内部,两条高在三角形外部,其交点在三角形外部.
知1-讲
感悟新知
3.表达方式:(1)AD是△ABC的边BC上的高;(2)AD⊥BC
于D;(3)∠ADC
=
90°,∠ADB
=
90°或∠ADC
=
∠ADB=90.注:上述三种情况都表示AD是高,选用哪种表示法,应根据解题需要.
4·易错警示:(1)三角形中大于90的角的两边上的高的作法(高均在三角形外部).
(2)任何三角形的三条商所在直线交于一点(垂心).
知1-讲
感悟新知
例
1
导引:“作一边上的高”可看作“过一点(这边所对角的顶点)作已知直线(这边所在直线)的垂线”.按照“过一点作已知直线的垂线”进行作图,顶点与垂足之间的线段即为该边上的高;需注意AB,BC边上的高在三角形的部,作高时先延长AB与CB.
<动手操作题,易错题>画出图中△
ABC的三条高.(要标明字母,不写画法)
知1-讲
感悟新知
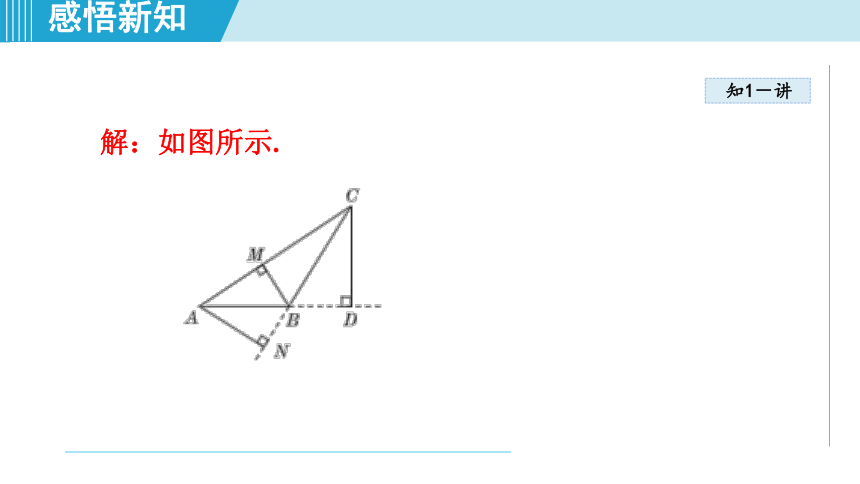
解:如图所示.
知1-讲
总
结
感悟新知
(1)作三角形的高时,找准顶点和对边是关键,作高的步骤就是“过一点作已知直线的垂线”的步骤:一靠(三角尺的一条直角边靠在要作高的边上);二找(移动三角尺使另一条直角边通过要作高的顶点);三画线(画垂线段),如图.
(2)注意:高是线段,垂线是直线.
知1-练
感悟新知
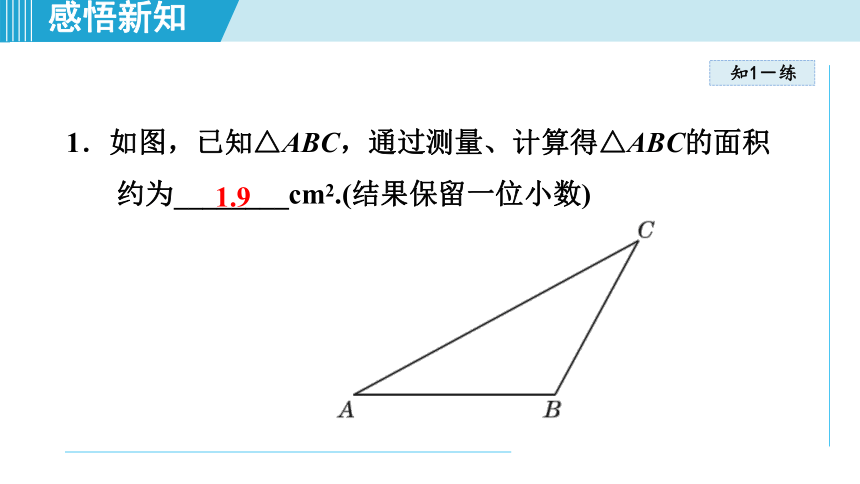
1.9
1.如图,已知△ABC,通过测量、计算得△ABC的面积约为________cm2.(结果保留一位小数)
知1-练
感悟新知
2.下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
知2-导
感悟新知
知识点
三角形的角平分线
2
在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线(angular
bisector)如图,∠BAD=∠CAD,则线段AD是△ABC的一条角平分线.
知2-讲
感悟新知
1.定义:在三角形中一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
2.位置图例:任何三角形的三条角平分线都交于一点,且该点在三角形的内部.如图.
知2-讲
感悟新知
3.表达方式:
(1)AD是△ABC的角平分线;
(2)AD平分2BAC交BC于点D;
(3)∠BAD
=∠CAD
=
∠BAC.
注:上述三种情况都表示同一意义,即AD是AABC的角平分线,选用哪种表示法,应根据解题需要.
4.易错警示:角平分线是一条射线,而三角形的角平分线是一条线段,不要混淆.
知2-讲
感悟新知
例2
关于三角形的角平分线,下列说法正确的是(
)
A.是线段
B.是射线
C.是直线
D.是射线或线段
导引:三角形的角平分线是一条线段,故选A.
A
知2-讲
感悟新知
总
结
角平线与三角形角平分线的比较
名称
组成的线
结果
图示
角平线
一条射线
得到两个相等的角
三角形的角平分线
一条线段
得到两个相等角
知2-练
感悟新知
C
1.如图,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;
⑤AE平分∠BAC.
A.4个
B.3个
C.2个
D.1个
知2-讲
感悟新知
如图所示,AD是△ABC的角平分线,AE是△ABD的角平分线,∠BAC=80°,则∠EAD的度数是(
)
A.20°
B.30°
C.45
°
D.60°
导引:由角平分线的性质,可得出∠EAD与∠BAD,∠BAC之间的数量关系.
A
例
3
知2-讲
感悟新知
解:因为AD平分∠BAC,∠BAC
=80°.
所以∠BAD=40°.
又因为AE平分∠BAD,所以∠EAD=20°.
故选A.
知2-讲
感悟新知
总
结
三角形的角平分线将三角形的内角分成相等的两部分,特别是两角之间的数量关系在求角的度数时起关键作用.
知2-练
感悟新知
D
知3-导
感悟新知
知识点
三角形的中线
3
在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线(median).如图,BE=EC,则线段AE是△ABC的BC边上的中线.
知3-导
感悟新知
任意画一个三角形,画出三边上的中线.你发现了什么?
知3-导
感悟新知
总
结
事实上,三角形的三条中线相交于一点.我们把这三条中线的交点叫作三角形的重心.如图,△ABC的三条中线AD,BE,CF相交于点G,则点G为△ABC的重心.
知3-讲
感悟新知
1.定义:在三角形中,连接一个顶点和它的对边中点的段叫作三角形的中线.
2.位置图例:任何三角形的三条中线都交于一点,且该点在三角形内部,如图,这个交点叫作三角形的重心.
知3-讲
感悟新知
3.表达方式:
(1)AD是△ABC中BC边上的中线;
(2)D是BC边的中点;
(3)BD
=
DC,BD=
BC,DC=
BC或BD=DC=
BC.
注:上述三种情况都表示AD是中线,选用哪种表示法,应根据解题需要.
4.易错警示:中线是线段,不要将它与线段所在直线混淆.
知3-讲
感悟新知
例4
如图,AD是△ABC
的中线,AE是△ABC的高.
(1)图中共有几个三角形?请分别列举出来.
(2)其中哪些三角形的面积相等?
解:(1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.
知3-讲
感悟新知
(2)因为AD是△ABC的中线,所以BD=DC.
因为AE是△ABC的高,也是△ABD和△ADC的高,又S△ABD=
BD
·
AE,S△ADC
=
DC·AE,
所以
S△ABD=
S△ADC
知3-讲
感悟新知
总
结
三角形的中线把三角形分成两个面积相等的三角形,得到两条相等的线段.
知3-讲
感悟新知
1.如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )
A.线段DE
B.线段BE
C.线段EF
D.线段FG
B
知3-讲
感悟新知
A
知3-讲
感悟新知
3.如图(1),已
知△ABC,画出△ABC中,BC边上的高、中线和∠BAC的平分线.
图(1)
知3-讲
感悟新知
分析:因为三角形的高、中线、角平分线都是描述性定义,它们的定义就蕴含了它们的画法,根据总结的画法画出图形即可,如图(2).
图(2)
知3-讲
感悟新知
解:画法如下:
(1)过A作BC的垂线,垂足为D,AD即为BC边上的高;
(2)取BC的中点E,连接AE,AE即为BC边上的中线;
(3)作∠BAC的平分线,交BC于点F,连接AF,AF即为△ABC中∠BAC的平分线.
知3-讲
感悟新知
<动手操作题>在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12cm和15
cm两部分,求△ABC的各边长.
导引:因为中线BD将△ABC的周长分成两部分:(BC+CD)和(AD+AB),无法确定谁为12cm,谁为15cm,故应分类讨论;另外题中涉及线段较多,因此可建立方程的模型,利用设未知数来求解.
例
5
知3-讲
感悟新知
解:设AB=x
cm,则AD=CD=
xcm.
(1)如图①,若AB
+AD=12
cm,则x+
x=12.
解得x=8,即AB=AC=8
cm,则CD=4
cm.
故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,所以三边长分别为8cm,8
cm,11
cm.
知3-讲
感悟新知
(2)如图②,若AB+AD=15
cm,则x+
x=15.
解得x=10,即AB=AC=10
cm,则CD
=5
cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10
cm,
10
cm,7
cm.
综上所述,AABC的三边长分别为8cm,8
cm,
11
cm或10
cm,10
cm,7
cm.
知3-讲
感悟新知
总
结
(1)本例中由于条件不确定,因此我们针对因条件的不确定性导致图形出现不同的情况,运用分类讨论思想对题目进行分类讨论;解答中,针对题中涉及的线段这个“形”较多,为了使解答更简练,我们将它们建立方程这个“数”的模型.因此本例的解答过程体现了:分类讨论思想、建模思想、数形结合思想、方程思想等.(2)警示:求三角形的边时,要注意隐含条件:三角形的三边关系.
知3-讲
感悟新知
1.等腰三角形一腰上的中线把这个三角形的周长分成为12
cm和15
cm两部分,求三角形的底边长.
分析:有两种可能,一种是锐角三角形,如图(1)所示,这时AB+AD=15
cm,BC+CD=12
cm;另一种是钝角三角形,如图(2),这时AB+AD=12
cm,BC+CD=15
cm.
图(1)
图(2)
知3-讲
感悟新知
知3-讲
感悟新知
知3-讲
感悟新知
2.如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线.
知3-讲
感悟新知
解:因为DE∥AC,
所以∠EDA=∠CAD.
因为∠EDA=∠EAD,
所以∠CAD=∠EAD,
所以AD是△ABC的角平分线.
课堂小结
知识总结
知识方法要点
关键总结
注意事项
三角形的三条重要线段
三角形的三条重要的线段是指三角形的内角平分线、三角形的三边的中线和三条高上的高线.
①三角形的角平分线、中线、高线都是线段;②三角形的三条角平分线交于一点,三条中线交于一点,三条高线交于一点:a.三角形的角平分线交于一点,交点在三角形的内部.b.三角形的三条中线的交点交于一点,交点在三角形的内部.c.锐角三角形三条高所在的直线的交点在三角形的内部;直角三角形三条高所在的直线的交点是直角顶点;钝角三角形三条高所在的直线的交点在三角形的外部.
三角形中的主要线段
课堂小结
三角形中的主要线段
方法规律总结
(1)三角形的三条角平分线,三条中线都在三角形内,而三角形的高却要看三角形的形状,锐角三角形的三条高在三角形内部,直角三角形两直角边上的高恰好是另一条直角边,而钝角三角形有两条高在三角形的外部,垂足落在边的延长线上.
(2)不论是一个三角形的三条角平分线还是三条中线,或者三条高线,“三线”或“三线”所在的直线都交于一点.
必做:
请完成教材课后习题
课后作业
作业
第1节
三角形
第2课时
三角形中的主要线段
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的高
三角形的角平分线
三角形的中线
课时导入
复习提问
引出问题
复习提问
引出问题
有一天,小明回家看到弟弟正在对着下边的三角形发呆,小明有一点奇怪了,外号“坐不住”的弟弟怎么能坐住了?原来是弟弟想作出三角形ABC的三条高,但是他不会作边AB、BC上的高,小明不假思索
的说:“我来帮你”,当他准备作时,也
难住了,聪明的你,能帮帮小明兄弟吗?
知识点
三角形的高
知1-导
感悟新知
1
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线(alitude),简称三角形的高.如图,AH⊥BC,垂足为点H,则线段AH
△ABC的BC边上的高.
知1-导
感悟新知
如图,试画出图中△ABC的BC边上的高.
知1-讲
感悟新知
1.定义:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做该三角形这条边上的高.一个三角形有三条高.
2.位置图例:
(1)锐角三角形:三条高都在三角形内部,
其交点也在三角形内部.
知1-讲
感悟新知
(2)直角三角形:一条高在三角形内部,两条高在三角形边上,其交点为直角顶点.
(3)钝角三角形:一条高在三角形内部,两条高在三角形外部,其交点在三角形外部.
知1-讲
感悟新知
3.表达方式:(1)AD是△ABC的边BC上的高;(2)AD⊥BC
于D;(3)∠ADC
=
90°,∠ADB
=
90°或∠ADC
=
∠ADB=90.注:上述三种情况都表示AD是高,选用哪种表示法,应根据解题需要.
4·易错警示:(1)三角形中大于90的角的两边上的高的作法(高均在三角形外部).
(2)任何三角形的三条商所在直线交于一点(垂心).
知1-讲
感悟新知
例
1
导引:“作一边上的高”可看作“过一点(这边所对角的顶点)作已知直线(这边所在直线)的垂线”.按照“过一点作已知直线的垂线”进行作图,顶点与垂足之间的线段即为该边上的高;需注意AB,BC边上的高在三角形的部,作高时先延长AB与CB.
<动手操作题,易错题>画出图中△
ABC的三条高.(要标明字母,不写画法)
知1-讲
感悟新知
解:如图所示.
知1-讲
总
结
感悟新知
(1)作三角形的高时,找准顶点和对边是关键,作高的步骤就是“过一点作已知直线的垂线”的步骤:一靠(三角尺的一条直角边靠在要作高的边上);二找(移动三角尺使另一条直角边通过要作高的顶点);三画线(画垂线段),如图.
(2)注意:高是线段,垂线是直线.
知1-练
感悟新知
1.9
1.如图,已知△ABC,通过测量、计算得△ABC的面积约为________cm2.(结果保留一位小数)
知1-练
感悟新知
2.下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
知2-导
感悟新知
知识点
三角形的角平分线
2
在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线(angular
bisector)如图,∠BAD=∠CAD,则线段AD是△ABC的一条角平分线.
知2-讲
感悟新知
1.定义:在三角形中一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
2.位置图例:任何三角形的三条角平分线都交于一点,且该点在三角形的内部.如图.
知2-讲
感悟新知
3.表达方式:
(1)AD是△ABC的角平分线;
(2)AD平分2BAC交BC于点D;
(3)∠BAD
=∠CAD
=
∠BAC.
注:上述三种情况都表示同一意义,即AD是AABC的角平分线,选用哪种表示法,应根据解题需要.
4.易错警示:角平分线是一条射线,而三角形的角平分线是一条线段,不要混淆.
知2-讲
感悟新知
例2
关于三角形的角平分线,下列说法正确的是(
)
A.是线段
B.是射线
C.是直线
D.是射线或线段
导引:三角形的角平分线是一条线段,故选A.
A
知2-讲
感悟新知
总
结
角平线与三角形角平分线的比较
名称
组成的线
结果
图示
角平线
一条射线
得到两个相等的角
三角形的角平分线
一条线段
得到两个相等角
知2-练
感悟新知
C
1.如图,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;
⑤AE平分∠BAC.
A.4个
B.3个
C.2个
D.1个
知2-讲
感悟新知
如图所示,AD是△ABC的角平分线,AE是△ABD的角平分线,∠BAC=80°,则∠EAD的度数是(
)
A.20°
B.30°
C.45
°
D.60°
导引:由角平分线的性质,可得出∠EAD与∠BAD,∠BAC之间的数量关系.
A
例
3
知2-讲
感悟新知
解:因为AD平分∠BAC,∠BAC
=80°.
所以∠BAD=40°.
又因为AE平分∠BAD,所以∠EAD=20°.
故选A.
知2-讲
感悟新知
总
结
三角形的角平分线将三角形的内角分成相等的两部分,特别是两角之间的数量关系在求角的度数时起关键作用.
知2-练
感悟新知
D
知3-导
感悟新知
知识点
三角形的中线
3
在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线(median).如图,BE=EC,则线段AE是△ABC的BC边上的中线.
知3-导
感悟新知
任意画一个三角形,画出三边上的中线.你发现了什么?
知3-导
感悟新知
总
结
事实上,三角形的三条中线相交于一点.我们把这三条中线的交点叫作三角形的重心.如图,△ABC的三条中线AD,BE,CF相交于点G,则点G为△ABC的重心.
知3-讲
感悟新知
1.定义:在三角形中,连接一个顶点和它的对边中点的段叫作三角形的中线.
2.位置图例:任何三角形的三条中线都交于一点,且该点在三角形内部,如图,这个交点叫作三角形的重心.
知3-讲
感悟新知
3.表达方式:
(1)AD是△ABC中BC边上的中线;
(2)D是BC边的中点;
(3)BD
=
DC,BD=
BC,DC=
BC或BD=DC=
BC.
注:上述三种情况都表示AD是中线,选用哪种表示法,应根据解题需要.
4.易错警示:中线是线段,不要将它与线段所在直线混淆.
知3-讲
感悟新知
例4
如图,AD是△ABC
的中线,AE是△ABC的高.
(1)图中共有几个三角形?请分别列举出来.
(2)其中哪些三角形的面积相等?
解:(1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.
知3-讲
感悟新知
(2)因为AD是△ABC的中线,所以BD=DC.
因为AE是△ABC的高,也是△ABD和△ADC的高,又S△ABD=
BD
·
AE,S△ADC
=
DC·AE,
所以
S△ABD=
S△ADC
知3-讲
感悟新知
总
结
三角形的中线把三角形分成两个面积相等的三角形,得到两条相等的线段.
知3-讲
感悟新知
1.如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )
A.线段DE
B.线段BE
C.线段EF
D.线段FG
B
知3-讲
感悟新知
A
知3-讲
感悟新知
3.如图(1),已
知△ABC,画出△ABC中,BC边上的高、中线和∠BAC的平分线.
图(1)
知3-讲
感悟新知
分析:因为三角形的高、中线、角平分线都是描述性定义,它们的定义就蕴含了它们的画法,根据总结的画法画出图形即可,如图(2).
图(2)
知3-讲
感悟新知
解:画法如下:
(1)过A作BC的垂线,垂足为D,AD即为BC边上的高;
(2)取BC的中点E,连接AE,AE即为BC边上的中线;
(3)作∠BAC的平分线,交BC于点F,连接AF,AF即为△ABC中∠BAC的平分线.
知3-讲
感悟新知
<动手操作题>在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12cm和15
cm两部分,求△ABC的各边长.
导引:因为中线BD将△ABC的周长分成两部分:(BC+CD)和(AD+AB),无法确定谁为12cm,谁为15cm,故应分类讨论;另外题中涉及线段较多,因此可建立方程的模型,利用设未知数来求解.
例
5
知3-讲
感悟新知
解:设AB=x
cm,则AD=CD=
xcm.
(1)如图①,若AB
+AD=12
cm,则x+
x=12.
解得x=8,即AB=AC=8
cm,则CD=4
cm.
故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,所以三边长分别为8cm,8
cm,11
cm.
知3-讲
感悟新知
(2)如图②,若AB+AD=15
cm,则x+
x=15.
解得x=10,即AB=AC=10
cm,则CD
=5
cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10
cm,
10
cm,7
cm.
综上所述,AABC的三边长分别为8cm,8
cm,
11
cm或10
cm,10
cm,7
cm.
知3-讲
感悟新知
总
结
(1)本例中由于条件不确定,因此我们针对因条件的不确定性导致图形出现不同的情况,运用分类讨论思想对题目进行分类讨论;解答中,针对题中涉及的线段这个“形”较多,为了使解答更简练,我们将它们建立方程这个“数”的模型.因此本例的解答过程体现了:分类讨论思想、建模思想、数形结合思想、方程思想等.(2)警示:求三角形的边时,要注意隐含条件:三角形的三边关系.
知3-讲
感悟新知
1.等腰三角形一腰上的中线把这个三角形的周长分成为12
cm和15
cm两部分,求三角形的底边长.
分析:有两种可能,一种是锐角三角形,如图(1)所示,这时AB+AD=15
cm,BC+CD=12
cm;另一种是钝角三角形,如图(2),这时AB+AD=12
cm,BC+CD=15
cm.
图(1)
图(2)
知3-讲
感悟新知
知3-讲
感悟新知
知3-讲
感悟新知
2.如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线.
知3-讲
感悟新知
解:因为DE∥AC,
所以∠EDA=∠CAD.
因为∠EDA=∠EAD,
所以∠CAD=∠EAD,
所以AD是△ABC的角平分线.
课堂小结
知识总结
知识方法要点
关键总结
注意事项
三角形的三条重要线段
三角形的三条重要的线段是指三角形的内角平分线、三角形的三边的中线和三条高上的高线.
①三角形的角平分线、中线、高线都是线段;②三角形的三条角平分线交于一点,三条中线交于一点,三条高线交于一点:a.三角形的角平分线交于一点,交点在三角形的内部.b.三角形的三条中线的交点交于一点,交点在三角形的内部.c.锐角三角形三条高所在的直线的交点在三角形的内部;直角三角形三条高所在的直线的交点是直角顶点;钝角三角形三条高所在的直线的交点在三角形的外部.
三角形中的主要线段
课堂小结
三角形中的主要线段
方法规律总结
(1)三角形的三条角平分线,三条中线都在三角形内,而三角形的高却要看三角形的形状,锐角三角形的三条高在三角形内部,直角三角形两直角边上的高恰好是另一条直角边,而钝角三角形有两条高在三角形的外部,垂足落在边的延长线上.
(2)不论是一个三角形的三条角平分线还是三条中线,或者三条高线,“三线”或“三线”所在的直线都交于一点.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
