湘教版八年级上数学2.1.3三角形的内角和课件(20张PPT)
文档属性
| 名称 | 湘教版八年级上数学2.1.3三角形的内角和课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第1节
三角形
第3课时
三角形的内角和
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的内角和定理
三角形内角和的应用
课时导入
复习提问
引出问题
复习提问
引出问题
三角形飞机
在2001年俄罗斯新发明了一款三角形多用途飞机,这是一种两人乘坐的小型飞机,飞机名为“克鲁伊兹”,由超轻型复合材料制成.飞机的机身呈三角形,机翼可在飞行员控制下灵活地变换飞行角度.“克鲁伊兹”配有特技飞行、领航和发动机参数控制系统,能够完成高难度的飞行动作且操作流程简便.它既可对林场、输电线路、石油管道进行多架次空中监护,为农田喷药施肥,又能搭载游客,使其亲身感受惊险的特技飞行.它的优良性能与三角形的特性是分不开的.三角形具有那些优良特性呢?学习了本章你就明白了.
知识点
三角形的内角和定理
知1-导
感悟新知
1
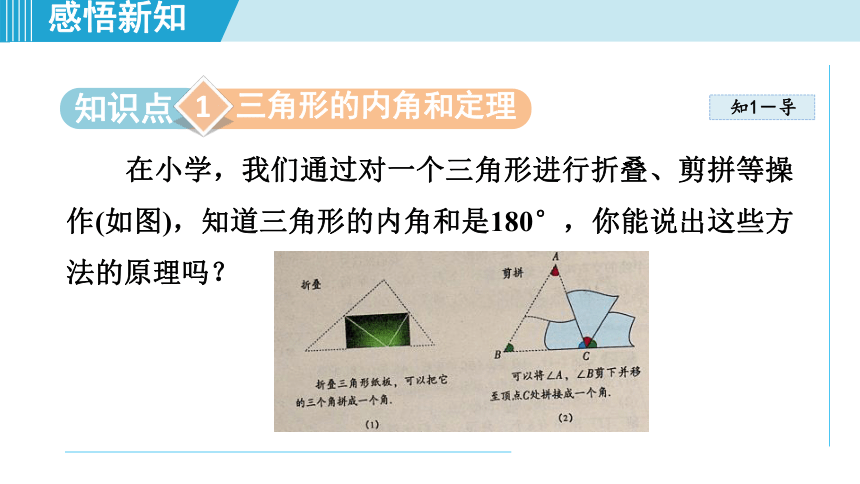
在小学,我们通过对一个三角形进行折叠、剪拼等操作(如图),知道三角形的内角和是180°,你能说出这些方法的原理吗?
知1-导
感悟新知
上述两种操作都是将三角形的三个内角拼到一起构成一个平角.
由此受到启发:如图,将△ABC的边BC所在的直线平移,使其像经过点A,得到直线B'C.
因为直线在平移下的像是与它平行的直线,所以B'C//BC.
则∠B'AB=∠B,∠C'AC=∠C.
又∠B'AB+∠BAC+∠C'AC=180,
所以
∠B+
∠BAC+∠C=180.
知1-导
结
论
感悟新知
三角的内角和等于180°
知1-讲
感悟新知
要点精析:
(1)在三角形中已知两个内角的度数,可以求出第三个内角的度数;
(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.
知1-讲
感悟新知
例
1
解:设∠B为x,则∠A为(3x)°,∠C为(x+
15)
°,从而有3x+x+(x+15)=180.解得x=33.
所以
3x=99,x+15=48.
答:∠A,∠B,∠C的度数分别为99°,33°,48°.
在△ABC中,∠A的度数是∠B的度数的3倍,∠C比∠B大15°,求∠A,∠B,∠C的度数.
知1-讲
总
结
感悟新知
求三角形的内角度数时,可根据三角形三个内角之间的关系设未知数,利用三角形内角和定理列出方程求解即可.
知1-练
感悟新知
B
1.三角形的内角和等于( )
A.90°
B.180°
C.270°
D.360°
2.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
D
知1-练
感悟新知
3.在△ABC中,已知∠A=40°,∠B=60°,则∠C的大小是______度.
解析:因为△ABC中,已知∠A=40°,∠B=60°,则∠C=180°-∠A-∠B=180°-40°-60°=80°.
80°
点拨:已知三角形的两个内角,直接用180°减去已知的两个角就是第三个内角的度数.
知2-讲
感悟新知
知识点
三角形内角和的应用
2
易错警示:在解决有关三角形的问题时,三角形的内角和等于180°,一般是作为隐含条件来用的,这一点在解决问题时切记.
知2-讲
感悟新知
例2
如图,在△
ABC中,AD是高,AE是∠BAC的平分线,∠B=20°,∠C=60°.求∠DAE的度数.
导引:∠DAE在△AED中,而∠DAE=∠BAD-∠BAE,要求DAE的度数,需先求出∠BAD和∠BAE的度数.
知2-讲
感悟新知
解:在△ABC中,∠B=20°,∠C=60°,
所以∠BAC=180°-∠B-∠C=100°.
又因为AE是∠BAC的平分线,
所以∠BAE=
∠BAC
=
×
100°=50°.
在△ABD中,∠B+
∠BAD+∠BDA=180.
又因为AD是高,所以∠BAD=
180°-20°-90°
=70°
所以∠DAE=
∠BAD-∠BAE=70°-50°=20
°.
知2-讲
感悟新知
总
结
灵活运用三角形内角和定理,结合三角形的高及角平分线的定义是求有关角的度数的常用方法.
知2-练
感悟新知
C
1.如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠C的度数是( )
A.50°
B.60°
C.70°
D.80°
2.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于( )
A.118°
B.119°
C.120°
D.121°
知2-练
感悟新知
C
3.锐角三角形的三个内角是∠A,∠B,∠C.如果∠α=∠A+∠B,∠β=∠B+∠C,∠γ=∠C+∠A,那么∠α,∠β,∠γ这三个角中( ).
A.没有锐角
B.有1个锐角
C.有2个锐角
D.有3个锐角
知2-练
感悟新知
A
课堂小结
三角形的内角和
1.任意一个三角形的三个内角和都等于180“,这是三角形中三角关系的一个非常重要的性质,当已知三角形的两个内角时,可以很容易求出第三个内角,例如,在△ABC中,如果∠A=30°,∠B=90°,那么∠C=180°-∠A-∠B=180°-30°-90°=60°.
2.三角形的三个内角中至少有两个是锐角,三角形中最大的角不小于60°.
必做:
请完成教材课后习题
课后作业
作业
第1节
三角形
第3课时
三角形的内角和
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的内角和定理
三角形内角和的应用
课时导入
复习提问
引出问题
复习提问
引出问题
三角形飞机
在2001年俄罗斯新发明了一款三角形多用途飞机,这是一种两人乘坐的小型飞机,飞机名为“克鲁伊兹”,由超轻型复合材料制成.飞机的机身呈三角形,机翼可在飞行员控制下灵活地变换飞行角度.“克鲁伊兹”配有特技飞行、领航和发动机参数控制系统,能够完成高难度的飞行动作且操作流程简便.它既可对林场、输电线路、石油管道进行多架次空中监护,为农田喷药施肥,又能搭载游客,使其亲身感受惊险的特技飞行.它的优良性能与三角形的特性是分不开的.三角形具有那些优良特性呢?学习了本章你就明白了.
知识点
三角形的内角和定理
知1-导
感悟新知
1
在小学,我们通过对一个三角形进行折叠、剪拼等操作(如图),知道三角形的内角和是180°,你能说出这些方法的原理吗?
知1-导
感悟新知
上述两种操作都是将三角形的三个内角拼到一起构成一个平角.
由此受到启发:如图,将△ABC的边BC所在的直线平移,使其像经过点A,得到直线B'C.
因为直线在平移下的像是与它平行的直线,所以B'C//BC.
则∠B'AB=∠B,∠C'AC=∠C.
又∠B'AB+∠BAC+∠C'AC=180,
所以
∠B+
∠BAC+∠C=180.
知1-导
结
论
感悟新知
三角的内角和等于180°
知1-讲
感悟新知
要点精析:
(1)在三角形中已知两个内角的度数,可以求出第三个内角的度数;
(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.
知1-讲
感悟新知
例
1
解:设∠B为x,则∠A为(3x)°,∠C为(x+
15)
°,从而有3x+x+(x+15)=180.解得x=33.
所以
3x=99,x+15=48.
答:∠A,∠B,∠C的度数分别为99°,33°,48°.
在△ABC中,∠A的度数是∠B的度数的3倍,∠C比∠B大15°,求∠A,∠B,∠C的度数.
知1-讲
总
结
感悟新知
求三角形的内角度数时,可根据三角形三个内角之间的关系设未知数,利用三角形内角和定理列出方程求解即可.
知1-练
感悟新知
B
1.三角形的内角和等于( )
A.90°
B.180°
C.270°
D.360°
2.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
D
知1-练
感悟新知
3.在△ABC中,已知∠A=40°,∠B=60°,则∠C的大小是______度.
解析:因为△ABC中,已知∠A=40°,∠B=60°,则∠C=180°-∠A-∠B=180°-40°-60°=80°.
80°
点拨:已知三角形的两个内角,直接用180°减去已知的两个角就是第三个内角的度数.
知2-讲
感悟新知
知识点
三角形内角和的应用
2
易错警示:在解决有关三角形的问题时,三角形的内角和等于180°,一般是作为隐含条件来用的,这一点在解决问题时切记.
知2-讲
感悟新知
例2
如图,在△
ABC中,AD是高,AE是∠BAC的平分线,∠B=20°,∠C=60°.求∠DAE的度数.
导引:∠DAE在△AED中,而∠DAE=∠BAD-∠BAE,要求DAE的度数,需先求出∠BAD和∠BAE的度数.
知2-讲
感悟新知
解:在△ABC中,∠B=20°,∠C=60°,
所以∠BAC=180°-∠B-∠C=100°.
又因为AE是∠BAC的平分线,
所以∠BAE=
∠BAC
=
×
100°=50°.
在△ABD中,∠B+
∠BAD+∠BDA=180.
又因为AD是高,所以∠BAD=
180°-20°-90°
=70°
所以∠DAE=
∠BAD-∠BAE=70°-50°=20
°.
知2-讲
感悟新知
总
结
灵活运用三角形内角和定理,结合三角形的高及角平分线的定义是求有关角的度数的常用方法.
知2-练
感悟新知
C
1.如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠C的度数是( )
A.50°
B.60°
C.70°
D.80°
2.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于( )
A.118°
B.119°
C.120°
D.121°
知2-练
感悟新知
C
3.锐角三角形的三个内角是∠A,∠B,∠C.如果∠α=∠A+∠B,∠β=∠B+∠C,∠γ=∠C+∠A,那么∠α,∠β,∠γ这三个角中( ).
A.没有锐角
B.有1个锐角
C.有2个锐角
D.有3个锐角
知2-练
感悟新知
A
课堂小结
三角形的内角和
1.任意一个三角形的三个内角和都等于180“,这是三角形中三角关系的一个非常重要的性质,当已知三角形的两个内角时,可以很容易求出第三个内角,例如,在△ABC中,如果∠A=30°,∠B=90°,那么∠C=180°-∠A-∠B=180°-30°-90°=60°.
2.三角形的三个内角中至少有两个是锐角,三角形中最大的角不小于60°.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
