湘教版八年级上数学2.1.5三角形的外角课件(21张PPT)
文档属性
| 名称 | 湘教版八年级上数学2.1.5三角形的外角课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 14:14:00 | ||
图片预览







文档简介
(共21张PPT)
第1节
三角形
第5课时
三角形的外角
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的外角定义
三角形的外角性质
三角形的外角的计算
课时导入
复习提问
引出问题
复习提问
引出问题
如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.你发现了什么?
知识点
三角形的外角定义
知1-导
感悟新知
1
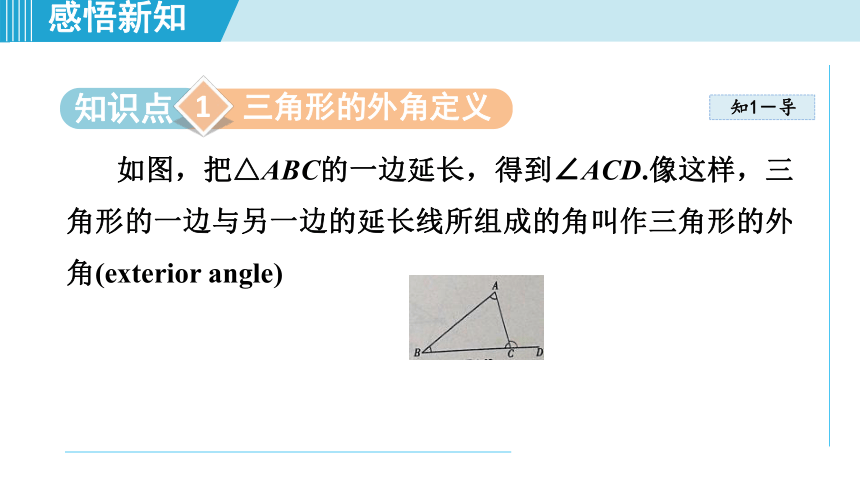
如图,把△ABC的一边延长,得到∠ACD.像这样,三角形的一边与另一边的延长线所组成的角叫作三角形的外角(exterior
angle)
知1-讲
感悟新知
要点精析:
(1)位置:在三角形的外部.
(2)与相邻内角是邻补角(即一边与内角一边公共,另一边是该内角另一边的反向延长线).
(3)三角形的每个顶点处都有两个外角,这两个外角是对顶角,我们研究三角形的外角时,通常只取其中一个.
知1-讲
感悟新知
例
1
导引:图中△CEF的三边的延长线只有EF的延长线FA,CE的延长线EB,延长线FA
与边CF构成的角为∠AFC;延长线EB与边EF构成的角为∠BEF.由三角形外角的概念可以判断∠AFC,
∠BEF是△CEF的外角.
如图,△CEF的外角为________________.
∠AFC,∠BEF
知1-讲
总
结
感悟新知
判定一个角是三角形的外角的三个条件:一是顶点在三角形的一个顶点上;二是一边是三角形的一条边;三是一边是三角形的另一条边的延长线.
知1-练
感悟新知
B
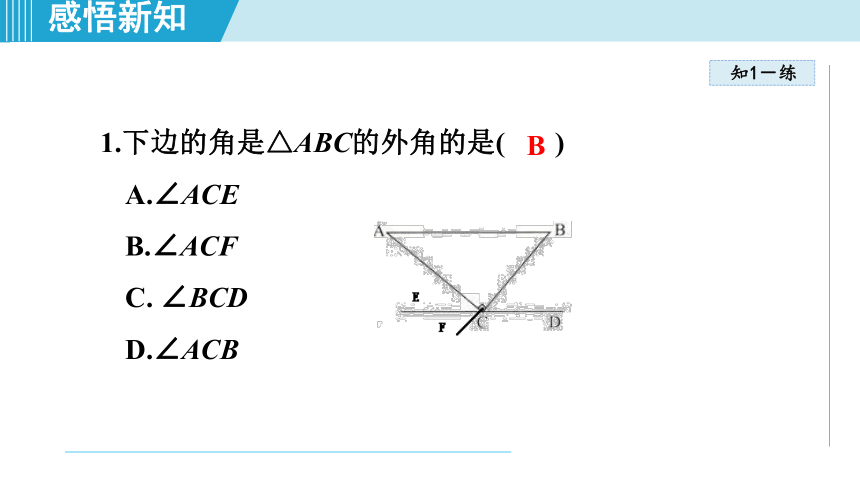
1.下边的角是△ABC的外角的是(
)
A.∠ACE
B.∠ACF
C.
∠BCD
D.∠ACB
知1-练
感悟新知
2.下列各图中,∠1是△ABC的外角的是( )
D
知2-导
感悟新知
知识点
三角形的外角性质
2
在图中,外角∠ACD
和与它不相邻的内角∠A,
∠B之间有什么大小关系?
因为∠ACD
+∠
ACB
=180°,
∠A+∠B+∠ACB
=180°,
所以∠ACD=∠A-∠B=0(等量减等量,差相等).
于是
∠ACD=∠A+∠B.
知2-讲
感悟新知
作用:
(1)此性质反映了三角形的外角与不相邻内角之间的数量关系,利用它可以求相关的角;
(2)利用它可以证明一个角等于另两个角的和或差;
(3)利用它作为中间关系证明两个角相等.
知2-讲
感悟新知
拓展:
(1)三角形不共顶点的三个外角的和等于360°,如图所示,∠1
+∠2+∠3
=
360°.
(2)三角形的一个外角大于任何一个和它不相邻的内角.如图所示,∠ACD
>
∠A,∠ACD
>
∠B.
知2-讲
感悟新知
例2
<浙江温州>如图,直线AB,CD被BC所截,若AB//CD,∠1=45°,∠2=35°,则∠3=______度.
导引:根据平行线的性质求出∠C,根据三角形外角性质求出即可.
解:因为AB//CD,∠1=45°,所以∠C=∠1=45°,
因为∠2=35°,所以∠3=∠2+∠C=35°+45°=
80°
,
80
知2-讲
感悟新知
总
结
利用三角形的外角的性质求角的度数常与内角的度数相结合来应用.
知2-练
感悟新知
C
1.如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A.120° B.90°
C.100° D.30°
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
C
知3-讲
感悟新知
知识点
三角形的外角性质
2
<山东威海>将一副直角三角板如图摆放,点C在EF
上,AC经过点D.已知∠A
=
∠EDF
=
90°,
∠E
=30°,∠BCE=
40°,则∠CDF=______.
例
3
25°
知3-讲
感悟新知
导引:要求∠CDF,则需求其余角∠2的度数.
∠2=180°
-∠1-∠ACB,其中∠1可利用三角形外角的性质求出,∠ACB为三角板内角已知.如图,由三角形外角的性质,知∠1
=∠E+∠BCE=
30°+40°=
70°,由三角形内角和定理知∠2=
180°-1-∠ACB
=
180°
-70°-45°=
65°,所以∠CDF
=∠EDF-∠2
=90°-65°=25°.
知3-讲
感悟新知
总
结
本题是以三角板为背景考查三角形外角的性质,是考试的一个热点;它主要是利用了三角板位置变换过程中其内角的度数不变的原理;解题时注意数形结合思想的应用,能从实物中抽象出所需的角是解题的关键.
1.如图,在△ABC中,在BC的延长线上取点D,E,连接AD,AE,则下列式子中正确的是( )
A.∠ACB>∠ACD
B.∠ACB>∠1+∠2+∠3
C.∠ACB>∠2+∠3
D.以上都正确
知3-练
感悟新知
C
课堂小结
三角形的外角
三角形的一个外角等于与它不相邻的两个内角的和,大于和它不相邻的任一内角.主要应用有:
(1)已知外角和与它不相邻的两个内角这三个角中的任意两个可求“另一个”.
(2)利用这个结论可证明一个角为另两个角的和.
(3)借助三角形内角和证明两个角相等.
(4)证明两角的不等关系.
必做:
请完成教材课后习题
课后作业
作业
第1节
三角形
第5课时
三角形的外角
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
三角形的外角定义
三角形的外角性质
三角形的外角的计算
课时导入
复习提问
引出问题
复习提问
引出问题
如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.你发现了什么?
知识点
三角形的外角定义
知1-导
感悟新知
1
如图,把△ABC的一边延长,得到∠ACD.像这样,三角形的一边与另一边的延长线所组成的角叫作三角形的外角(exterior
angle)
知1-讲
感悟新知
要点精析:
(1)位置:在三角形的外部.
(2)与相邻内角是邻补角(即一边与内角一边公共,另一边是该内角另一边的反向延长线).
(3)三角形的每个顶点处都有两个外角,这两个外角是对顶角,我们研究三角形的外角时,通常只取其中一个.
知1-讲
感悟新知
例
1
导引:图中△CEF的三边的延长线只有EF的延长线FA,CE的延长线EB,延长线FA
与边CF构成的角为∠AFC;延长线EB与边EF构成的角为∠BEF.由三角形外角的概念可以判断∠AFC,
∠BEF是△CEF的外角.
如图,△CEF的外角为________________.
∠AFC,∠BEF
知1-讲
总
结
感悟新知
判定一个角是三角形的外角的三个条件:一是顶点在三角形的一个顶点上;二是一边是三角形的一条边;三是一边是三角形的另一条边的延长线.
知1-练
感悟新知
B
1.下边的角是△ABC的外角的是(
)
A.∠ACE
B.∠ACF
C.
∠BCD
D.∠ACB
知1-练
感悟新知
2.下列各图中,∠1是△ABC的外角的是( )
D
知2-导
感悟新知
知识点
三角形的外角性质
2
在图中,外角∠ACD
和与它不相邻的内角∠A,
∠B之间有什么大小关系?
因为∠ACD
+∠
ACB
=180°,
∠A+∠B+∠ACB
=180°,
所以∠ACD=∠A-∠B=0(等量减等量,差相等).
于是
∠ACD=∠A+∠B.
知2-讲
感悟新知
作用:
(1)此性质反映了三角形的外角与不相邻内角之间的数量关系,利用它可以求相关的角;
(2)利用它可以证明一个角等于另两个角的和或差;
(3)利用它作为中间关系证明两个角相等.
知2-讲
感悟新知
拓展:
(1)三角形不共顶点的三个外角的和等于360°,如图所示,∠1
+∠2+∠3
=
360°.
(2)三角形的一个外角大于任何一个和它不相邻的内角.如图所示,∠ACD
>
∠A,∠ACD
>
∠B.
知2-讲
感悟新知
例2
<浙江温州>如图,直线AB,CD被BC所截,若AB//CD,∠1=45°,∠2=35°,则∠3=______度.
导引:根据平行线的性质求出∠C,根据三角形外角性质求出即可.
解:因为AB//CD,∠1=45°,所以∠C=∠1=45°,
因为∠2=35°,所以∠3=∠2+∠C=35°+45°=
80°
,
80
知2-讲
感悟新知
总
结
利用三角形的外角的性质求角的度数常与内角的度数相结合来应用.
知2-练
感悟新知
C
1.如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A.120° B.90°
C.100° D.30°
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
C
知3-讲
感悟新知
知识点
三角形的外角性质
2
<山东威海>将一副直角三角板如图摆放,点C在EF
上,AC经过点D.已知∠A
=
∠EDF
=
90°,
∠E
=30°,∠BCE=
40°,则∠CDF=______.
例
3
25°
知3-讲
感悟新知
导引:要求∠CDF,则需求其余角∠2的度数.
∠2=180°
-∠1-∠ACB,其中∠1可利用三角形外角的性质求出,∠ACB为三角板内角已知.如图,由三角形外角的性质,知∠1
=∠E+∠BCE=
30°+40°=
70°,由三角形内角和定理知∠2=
180°-1-∠ACB
=
180°
-70°-45°=
65°,所以∠CDF
=∠EDF-∠2
=90°-65°=25°.
知3-讲
感悟新知
总
结
本题是以三角板为背景考查三角形外角的性质,是考试的一个热点;它主要是利用了三角板位置变换过程中其内角的度数不变的原理;解题时注意数形结合思想的应用,能从实物中抽象出所需的角是解题的关键.
1.如图,在△ABC中,在BC的延长线上取点D,E,连接AD,AE,则下列式子中正确的是( )
A.∠ACB>∠ACD
B.∠ACB>∠1+∠2+∠3
C.∠ACB>∠2+∠3
D.以上都正确
知3-练
感悟新知
C
课堂小结
三角形的外角
三角形的一个外角等于与它不相邻的两个内角的和,大于和它不相邻的任一内角.主要应用有:
(1)已知外角和与它不相邻的两个内角这三个角中的任意两个可求“另一个”.
(2)利用这个结论可证明一个角为另两个角的和.
(3)借助三角形内角和证明两个角相等.
(4)证明两角的不等关系.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
