湘教版八年级上数学 2.3.1等腰三角形的性质 课件(36张PPT)
文档属性
| 名称 | 湘教版八年级上数学 2.3.1等腰三角形的性质 课件(36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 14:17:58 | ||
图片预览










文档简介
(共36张PPT)
第3节
等腰三角形
第1课时
等腰三角形的性质
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
等边对等角
等要三角形的轴对称性:“三线合一”
等边三角形的性质
课时导入
复习提问
引出问题
复习提问
引出问题
将一把三角尺和一个重锤如图放置,就能检查一根横渠是否水平,你知道为什么吗?
知识点
等边对等角
知1-导
感悟新知
1
“任意画一个等腰三角形,……你发现了什么?”
知1-讲
结
论
感悟新知
等腰三角形的两底角相等(简称“等边对等角”)
特别解读
1.
适用条件:必须在同一个三角形中.
2.
作用:证明角相等的常用方法.
知1-讲
感悟新知
1.“等边对等角”必须在同一个三角形中,如果在两个三角形中有两条边对应相等,那么它们所对的两个角不一定相等.
2.
利用等腰三角形的性质可以由边相等得到角相等
知1-讲
感悟新知
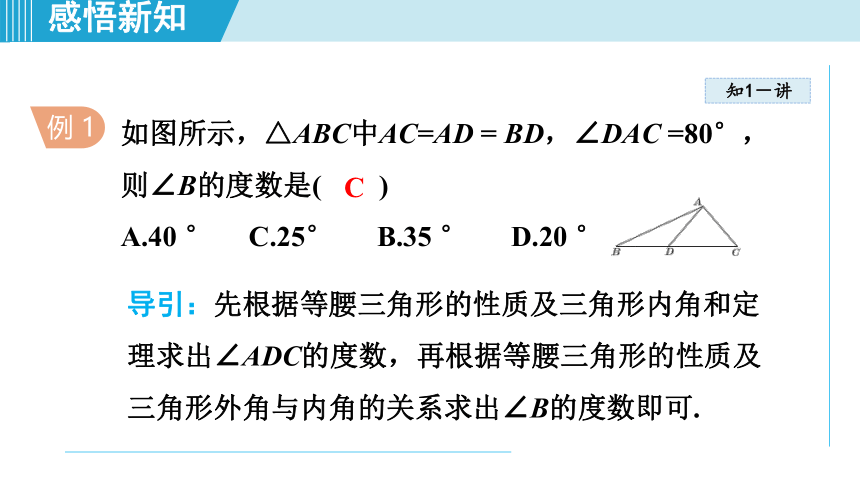
例
1
导引:先根据等腰三角形的性质及三角形内角和定理求出∠ADC的度数,再根据等腰三角形的性质及三角形外角与内角的关系求出∠B的度数即可.
如图所示,△ABC中AC=AD
=
BD,∠DAC
=80°,则∠B的度数是(
)
A.40
°
C.25°
B.35
°
D.20
°
C
知1-讲
总
结
感悟新知
在等腰三角形中求角的度数,一定要考虑到三角形内角和定理及三角形外角与内角的关系.
知1-练
感悟新知
C
1.如图,在等腰三角形ABC中,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,连接BE,则下列结论一定正确的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
2.如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A.30°
B.35°
C.40°
D.45°
知1-练
感悟新知
C
3.如图,AD、BC相交于O,AB∥CD,OA=OB,求证:∠C=∠D.
知1-练
感悟新知
分析:由等腰三角形的性质易得∠A=∠B,由平行线的性质可得∠A=∠D,∠B=∠C,等量代换即得∠C=∠D.
知1-练
感悟新知
证明:∵OA=OB,∴∠A=∠B.
∵AB∥CD,∴∠A=∠D,∠B=∠C.
∴∠C=∠D.
知2-导
感悟新知
知识点
等腰三角形的轴对称性:“三线合一”
2
任意画一个等腰三角形ABC,其中AB=AC,如图,作△ABC关于顶角平分线AD所在直线的轴反射,由于∠1=∠2,AB=AC,因此:
射线AB的像是射线AC,射线AC的像是射线______;
线段AB的是线段AC,线段AC的像是线段______;
点B的像是点C,点C的像是点______;
段BC的像是线段CB.
知2-导
感悟新知
从而等腰三角形ABC关于直线________对称.
由于点D的像是点D,因此线段DB的像是线段________,从而AD是底边BC上的________.
由于射线DB的像是射线DC,射线DA的像是射线________,因此∠BDA
_______∠CDA=________°,从而AD是底边BC上的_________.
由于射线BA的像是射线CA,射线BC的像是射线________,因此∠B
________∠C.
知2-导
感悟新知
结
论
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形底边上的高、中线及顶角平分线重合(简称“三线合一“).
知2-导
感悟新知
特别解读
1.
适用条件:
(1)必须是等腰三角形,
(2)必须是底边上的高、底边上的中线和顶角平分线才相互重合.
2.
作用:是证明线段相等、角相等、线段垂直等关系的重要方法.
知2-讲
感悟新知
不能说等腰三角形的对称轴是顶角平分线,因为对称轴是直线.
知2-讲
感悟新知
例2
已知:如图,在△ABC中,AB=AC点D,E在边BC上,且AD=AE.求证:BD=CE.
知2-讲
感悟新知
证明:作AF⊥BC,垂足为点F,则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线.
∴BF=CF,DF=EF,
∴BF-DF=CF-EF,即BD=CE.
知2-讲
感悟新知
总
结
此题考查了“三线合一”性质的实际应用.
知2-练
感悟新知
C
1.如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
2.如图,在△ABC中,AB=AC,AD⊥BC,交BC于D,BD=5
cm,求底边BC的长.
知2-练
感悟新知
分析:因为是等腰三角形,所以底边上的
高也是底边上的中线,所以BC=2BD,即可求出BC的长.
解:因为AB=AC,AD⊥BC,
所以BC=2BD=2×5=10(cm).
答:底边BC的长是10
cm.
知识点
等边三角形的性质
知3-导
感悟新知
3
如图,△ABC等边三角形,那么∠A,∠B,∠C的大小之间有什么关系呢?
解:如图,因为△ABC是等边三角形,
所以AB=BC-AC,从而∠C=∠A=∠B.
由三角形内角和定理可得:
∠A=
∠B=∠C=60°.
知3-讲
结
论
感悟新知
等边三角形的三个内角相等,且都等于60°.
知3-讲
感悟新知
要点精析:由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
知3-讲
感悟新知
例
3
如下图所示,在等边三角形ABC中,∠B、∠C的角平分线交于点O,OB和OC的垂直平分线分别交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
知3-讲
感悟新知
证明:如下图,分别连接OE、OF,
∵E、F分别是OB、OC垂直平分线上的点,
∴OE=BE,CF=OF.
∴
∠OBE=∠BOE.
∵△ABC为等边三角形,∴∠ABC=60°.
知3-讲
感悟新知
∵OB平分∠ABC,
∴∠OBE=
∠ABC=
×60°=30°.
∴∠OEF=∠OBE+∠BOE=60°.
同理∠OFE=60°,
∴△OEF为等边三角形.
∴OE=OF=EF.∴BE=EF=FC.
知3-讲
结
论
感悟新知
等边三角形是特殊的等腰三角形,等边三角形具有等腰三角形的一切性质.
1.如图,在等边三角形ABC中,AD⊥BC,垂足为点D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15°
B.30°
C.45°
D.60°
知3-练
感悟新知
A
2.如图,△ABC是等边三角形,AD是∠BAC的平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
A.3
B.2
C.1
D.0
知3-练
感悟新知
A
3.如图所示,△ABC是等边三角形,AE⊥BC于点E,则下列结论不正确的是(
)
A.AB=AC=BC
B.∠BAC=∠ABC=∠ACB=60°
C.AE是△ABC唯一的一条对称轴
D.AE是∠BAC的平分线
知3-练
感悟新知
知3-练
感悟新知
【答案】C
分析:A,B,D结论正确.C不正确.AE是△ABC的对称轴,但不是唯一的,等边三角形ABC还有两条对称轴,分别是AC,AB两边上的高.
课堂小结
1.等腰三角形的性质定理1及推论
等腰三角形的性质定理1:等腰三角形的两个底角相等,也可以说成,在同一个三角形中,等边对等角.
注意:(1)“等边对等角”只限于在同一个三角形中,若两个三角形中有两边对应相等,那么它们所对的角不一定相等.(2)等腰三角形的顶角可能是锐角、直角或纯角,而底角只能是锐角.(3)在已知锐角的情况下,需要分类讨论该锐角是顶角,还是底角.
等腰三角形的性质
课堂小结
等腰三角形的性质
2.等腰三角形中求角的度数的“三种方法”
(1)利用等边对等角得相等的角.
(2)利用三角形外角等于与其不相邻的两内角之和导出各角之间的关系.
(3)利用三角形内角和定理列方程.
必做:
请完成教材课后习题
课后作业
作业
第3节
等腰三角形
第1课时
等腰三角形的性质
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
等边对等角
等要三角形的轴对称性:“三线合一”
等边三角形的性质
课时导入
复习提问
引出问题
复习提问
引出问题
将一把三角尺和一个重锤如图放置,就能检查一根横渠是否水平,你知道为什么吗?
知识点
等边对等角
知1-导
感悟新知
1
“任意画一个等腰三角形,……你发现了什么?”
知1-讲
结
论
感悟新知
等腰三角形的两底角相等(简称“等边对等角”)
特别解读
1.
适用条件:必须在同一个三角形中.
2.
作用:证明角相等的常用方法.
知1-讲
感悟新知
1.“等边对等角”必须在同一个三角形中,如果在两个三角形中有两条边对应相等,那么它们所对的两个角不一定相等.
2.
利用等腰三角形的性质可以由边相等得到角相等
知1-讲
感悟新知
例
1
导引:先根据等腰三角形的性质及三角形内角和定理求出∠ADC的度数,再根据等腰三角形的性质及三角形外角与内角的关系求出∠B的度数即可.
如图所示,△ABC中AC=AD
=
BD,∠DAC
=80°,则∠B的度数是(
)
A.40
°
C.25°
B.35
°
D.20
°
C
知1-讲
总
结
感悟新知
在等腰三角形中求角的度数,一定要考虑到三角形内角和定理及三角形外角与内角的关系.
知1-练
感悟新知
C
1.如图,在等腰三角形ABC中,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,连接BE,则下列结论一定正确的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
2.如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A.30°
B.35°
C.40°
D.45°
知1-练
感悟新知
C
3.如图,AD、BC相交于O,AB∥CD,OA=OB,求证:∠C=∠D.
知1-练
感悟新知
分析:由等腰三角形的性质易得∠A=∠B,由平行线的性质可得∠A=∠D,∠B=∠C,等量代换即得∠C=∠D.
知1-练
感悟新知
证明:∵OA=OB,∴∠A=∠B.
∵AB∥CD,∴∠A=∠D,∠B=∠C.
∴∠C=∠D.
知2-导
感悟新知
知识点
等腰三角形的轴对称性:“三线合一”
2
任意画一个等腰三角形ABC,其中AB=AC,如图,作△ABC关于顶角平分线AD所在直线的轴反射,由于∠1=∠2,AB=AC,因此:
射线AB的像是射线AC,射线AC的像是射线______;
线段AB的是线段AC,线段AC的像是线段______;
点B的像是点C,点C的像是点______;
段BC的像是线段CB.
知2-导
感悟新知
从而等腰三角形ABC关于直线________对称.
由于点D的像是点D,因此线段DB的像是线段________,从而AD是底边BC上的________.
由于射线DB的像是射线DC,射线DA的像是射线________,因此∠BDA
_______∠CDA=________°,从而AD是底边BC上的_________.
由于射线BA的像是射线CA,射线BC的像是射线________,因此∠B
________∠C.
知2-导
感悟新知
结
论
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形底边上的高、中线及顶角平分线重合(简称“三线合一“).
知2-导
感悟新知
特别解读
1.
适用条件:
(1)必须是等腰三角形,
(2)必须是底边上的高、底边上的中线和顶角平分线才相互重合.
2.
作用:是证明线段相等、角相等、线段垂直等关系的重要方法.
知2-讲
感悟新知
不能说等腰三角形的对称轴是顶角平分线,因为对称轴是直线.
知2-讲
感悟新知
例2
已知:如图,在△ABC中,AB=AC点D,E在边BC上,且AD=AE.求证:BD=CE.
知2-讲
感悟新知
证明:作AF⊥BC,垂足为点F,则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线.
∴BF=CF,DF=EF,
∴BF-DF=CF-EF,即BD=CE.
知2-讲
感悟新知
总
结
此题考查了“三线合一”性质的实际应用.
知2-练
感悟新知
C
1.如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
2.如图,在△ABC中,AB=AC,AD⊥BC,交BC于D,BD=5
cm,求底边BC的长.
知2-练
感悟新知
分析:因为是等腰三角形,所以底边上的
高也是底边上的中线,所以BC=2BD,即可求出BC的长.
解:因为AB=AC,AD⊥BC,
所以BC=2BD=2×5=10(cm).
答:底边BC的长是10
cm.
知识点
等边三角形的性质
知3-导
感悟新知
3
如图,△ABC等边三角形,那么∠A,∠B,∠C的大小之间有什么关系呢?
解:如图,因为△ABC是等边三角形,
所以AB=BC-AC,从而∠C=∠A=∠B.
由三角形内角和定理可得:
∠A=
∠B=∠C=60°.
知3-讲
结
论
感悟新知
等边三角形的三个内角相等,且都等于60°.
知3-讲
感悟新知
要点精析:由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
知3-讲
感悟新知
例
3
如下图所示,在等边三角形ABC中,∠B、∠C的角平分线交于点O,OB和OC的垂直平分线分别交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
知3-讲
感悟新知
证明:如下图,分别连接OE、OF,
∵E、F分别是OB、OC垂直平分线上的点,
∴OE=BE,CF=OF.
∴
∠OBE=∠BOE.
∵△ABC为等边三角形,∴∠ABC=60°.
知3-讲
感悟新知
∵OB平分∠ABC,
∴∠OBE=
∠ABC=
×60°=30°.
∴∠OEF=∠OBE+∠BOE=60°.
同理∠OFE=60°,
∴△OEF为等边三角形.
∴OE=OF=EF.∴BE=EF=FC.
知3-讲
结
论
感悟新知
等边三角形是特殊的等腰三角形,等边三角形具有等腰三角形的一切性质.
1.如图,在等边三角形ABC中,AD⊥BC,垂足为点D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15°
B.30°
C.45°
D.60°
知3-练
感悟新知
A
2.如图,△ABC是等边三角形,AD是∠BAC的平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
A.3
B.2
C.1
D.0
知3-练
感悟新知
A
3.如图所示,△ABC是等边三角形,AE⊥BC于点E,则下列结论不正确的是(
)
A.AB=AC=BC
B.∠BAC=∠ABC=∠ACB=60°
C.AE是△ABC唯一的一条对称轴
D.AE是∠BAC的平分线
知3-练
感悟新知
知3-练
感悟新知
【答案】C
分析:A,B,D结论正确.C不正确.AE是△ABC的对称轴,但不是唯一的,等边三角形ABC还有两条对称轴,分别是AC,AB两边上的高.
课堂小结
1.等腰三角形的性质定理1及推论
等腰三角形的性质定理1:等腰三角形的两个底角相等,也可以说成,在同一个三角形中,等边对等角.
注意:(1)“等边对等角”只限于在同一个三角形中,若两个三角形中有两边对应相等,那么它们所对的角不一定相等.(2)等腰三角形的顶角可能是锐角、直角或纯角,而底角只能是锐角.(3)在已知锐角的情况下,需要分类讨论该锐角是顶角,还是底角.
等腰三角形的性质
课堂小结
等腰三角形的性质
2.等腰三角形中求角的度数的“三种方法”
(1)利用等边对等角得相等的角.
(2)利用三角形外角等于与其不相邻的两内角之和导出各角之间的关系.
(3)利用三角形内角和定理列方程.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
