湘教版八年级上数学 2.5.4用“边边边”判定三角形全等 课件(30张PPT)
文档属性
| 名称 | 湘教版八年级上数学 2.5.4用“边边边”判定三角形全等 课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 14:26:30 | ||
图片预览









文档简介
(共30张PPT)
第5节
全等
三角形
第4课时
用“边边边”判定三角形全等
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
“边边边”(SSS)
全等三角形的判定(SSS)的应用
三角形的稳定性
课时导入
复习提问
引出问题
复习提问
引出问题
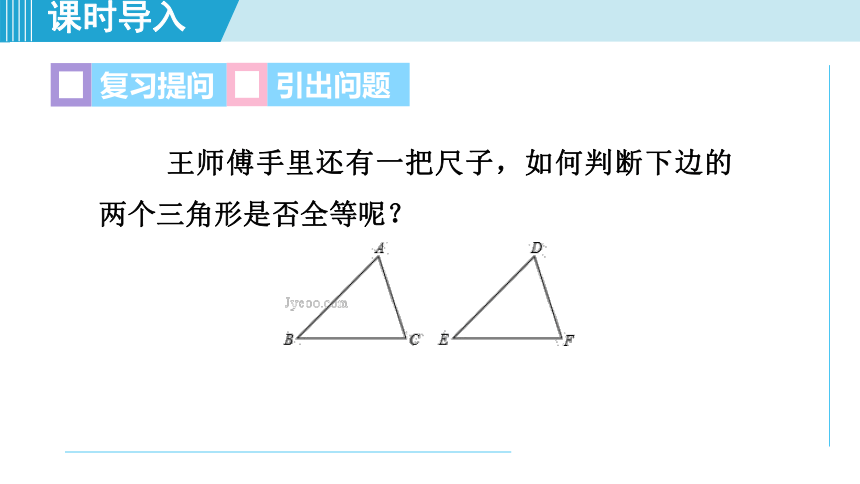
王师傅手里还有一把尺子,如何判断下边的两个三角形是否全等呢?
知识点
“边边边”(SSS)
知1-导
感悟新知
1
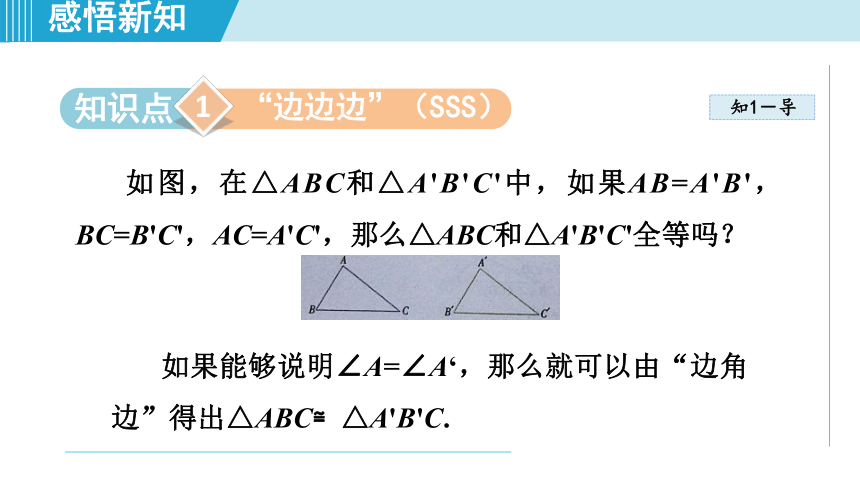
如图,在△ABC和△A'B'C'中,如果AB=A'B',BC=B'C',AC=A'C',那么△ABC和△A'B'C'全等吗?
如果能够说明∠A=∠A‘,那么就可以由“边角边”得出△ABC≌△A'B'C.
知1-导
感悟新知
将△ABC作平移、旋转和轴反射等变换,使BC的像B"C”与B'C'重合,并使点A的像A"与点A'在B'C'的两旁,△ABC在上述变换下的像为△
A"B"C",如图,由上述变换性质可知△ABC
≌△
A"B'C',则AB=A"B'=
A'B',AC=A"C'=A'C'.连接A'A".
知1-导
感悟新知
∵A'B'=A"B',A'C'=A"C',
∴∠1=∠2,∠3=∠4.从而∠1+∠3=∠2+∠4,
即
∠B'A'C'=∠B'A"C.
在∠A'B'C'和∠A"B'C'中,
A'B'=A"B',
∠B'A'C'=
∠B'A"C',A'C'=A"C',
∴△A'B'C'≌△
A"B'C'
(SAS).
∴△ABC
≌△
A'B'C'.
知1-讲
结
论
感悟新知
三边分别相等的两个三角形全等.
知1-讲
感悟新知
1.证明书写格式:在△ABC和△A'B'C'中
AB
=A'B,
∵
AC=A'C'',∴△ABC≌△A'B'C.
BC=B'C',
知1-讲
感悟新知
要点精析:
(1)全等的元素:三边.
(2)在判定两三角形全等的书写过程中,等号左边是全等号左边三角形的三边,等号右边是全等号右边三角形的三边,即前后顺序要保持一致.
(3)书写过程中的边及三角形的顶点前后顺序要对应.
知1-讲
感悟新知
3.三角形全等的判定方法:在两个三角形的六个元素中(三条边和三个角),可以判断两个三角形全等的组合有4个:"SSS,SAS,ASA,AAS";不能判定两个三角形全等的组合有2个:"AAA,SSA".
知1-讲
感悟新知
例
1
已知:如图,AB=CD,BC=DA.
求证:∠B=∠D.
证明
在△ABC和△CDA中,AB=CD,
BC=DA,
AC=CA(公共边),
∴△ABC≌△CDA(SSS).
∴∠B=∠D.
知1-讲
总
结
感悟新知
综合法:利用某些已经证明过的结论和性质及已知条件,推导出所要证明的结论成立的方法叫综合法,其思维特点是:由因索果,即从已知条件出发,利用已知的数学定理、性质和公式,推出结论,本书的证明基本上都是用综合法.
本题运用了综合法,根据条件用"SSS"可得到全等的三角形,从全等三角形出发可找到与结论有关的相等的角.
知1-练
感悟新知
C
1.下列三角形中,与如图所示的△ABC全等的是( )
2.如图,已知AB=AC,AE=AD,点B,D,E,C在同一条直线上,要利用“SSS”推理得出△ABE≌△ACD,还需要添加的一个条件可以是( )
A.BD=DE
B.BD=CE
C.DE=CE
D.以上都不对
知1-练
感悟新知
B
3.
如图所示,若AB=CD,AD=CB,∠B=25°,则∠D=________°.
知1-练
感悟新知
分析:如图所示,连接AC,因为AC=AC,AB=CD,AD=CB,所以△ABC≌△CDA,所以∠D=∠B=25°.
25
知2-导
感悟新知
知识点
全等三角形的判定(SSS)的应用
2
已知:如图,AC与BD相交于点O,且AB=DC,AC=DE求证:∠A=∠D.
例2
知2-讲
感悟新知
证明
连接BC.
在△ABC和△DCB中,
AB=DC,
BC=CB(公共边),
AC=DB,
∴△ABC≌△DCB(SSS).
∴∠A=∠D.
知2-讲
感悟新知
总
结
综合法:利用某些已经证明过的结论和性质及已知条件,推导出所要证明的结论成立的方法叫综合法,其思维特点是:由因索果,即从已知条件出发,利用已知的数学定理、性质和公式,推出结论.本书的证明基本上都是用综合法.
本题运用了综合法,根据条件用"SSS"可得到全等的三角形,从全等三角形出发可找到与结论有关的相等的角.
1.如图,AB=CD,BC=DA,E,F是AC上两点,且AE=CF,DE=BF,那么图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
知2-练
感悟新知
C
2.如图,在△ABC和△DCB中,AB
=
DC,AC
=
DB,AC与DB交于点M.则△ABC与△DCB
全等吗?请说明理由.
知2-练
感悟新知
分析:要想说明△ABC≌△DCB,因为AB
=
DC,AC
=
DB,观察图形,因为BC是两个三角形的公共边,根据“边边边”,可得△ABC≌△DCB.
知2-练
感悟新知
解:全等.
理由是:因为在△ABC和△DCB中,AB
=
DC,AC
=
DB,BC=CB
所以△ABC≌△DCB(SSS)
知识点
三角形的稳定性
知3-导
感悟新知
3
由“边边边”可知,只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
三角形的稳定性在生产和生活中有广泛的应用,如日常生活中的定位锁、房屋的人字梁屋
顶等都采用三角形结构,其道理就
是运用三角形的稳定性.
知3-讲
感悟新知
1.三角形的稳定性:只要三角形三边的长度确定,那么这三角形的形状和大小也就固定了,三角形的这个性质,叫作三角形的稳定性.
2.四边及四边以上的图形不具有稳定性,为保证其稳定,常在多边形中构造三角形.
注意:稳定性是三角形的特性,其他图形都不具有稳定性.
知3-讲
感悟新知
例
3
<探究题>要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架呢?六边形呢?n边形呢?
导引:若要多边形稳定,需将它变换成若干个三角形.先画出图形,结合图形分割三角形得出:四边形:1根,五边形:2根,六边形:3根,由类比推理可知,n边形:(n-3)根,如图所示.
知3-讲
感悟新知
解:四边形木架至少要再钉上1根,五边形木架:2根,六边形木架:3根,n边形木架:(n-3)根.
知3-讲
结
论
感悟新知
(1)本题运用了数形结合思想,使问题更直观、易懂,还运用了从特殊到一般的思想,由四边形、五边形、六边形类比出n边形,此题为一道规律探究题,通过观察图形,分析、归纳其中的规律.
(2)从特殊到一般的思想是一种重要的数学思想方法,其特点是通过对特殊现象的认识,利用归纳、类比、猜想、探索发现一般的规律,如一般性的结论、解决问题的方法等.
1.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?
答:____________.(填“稳定
性”或“不稳定性”)
知3-练
感悟新知
稳定性
2.不是利用三角形稳定性的是(
)
A.自行车的三角形车架
B.三角形房架
C.照相机的三角架
D.矩形门框的斜拉条
知3-练
感悟新知
C
课堂小结
用“边边边”判定三角形全等
1.证明三角形全等时,除了充分应用题目提供的条件外,还应仔细观察图形,充分挖掘题目图形中的隐含条件,如公共边.
2.
利用“边边边”判断三角形全等时,当所给相等的边不是要判定的三角形的边时,往往利用等式的性质,在相等线段两边加上或减去同一(相等)线段,转化为两个三角形的边.
必做:
请完成教材课后习题
课后作业
作业
第5节
全等
三角形
第4课时
用“边边边”判定三角形全等
第2章
三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
“边边边”(SSS)
全等三角形的判定(SSS)的应用
三角形的稳定性
课时导入
复习提问
引出问题
复习提问
引出问题
王师傅手里还有一把尺子,如何判断下边的两个三角形是否全等呢?
知识点
“边边边”(SSS)
知1-导
感悟新知
1
如图,在△ABC和△A'B'C'中,如果AB=A'B',BC=B'C',AC=A'C',那么△ABC和△A'B'C'全等吗?
如果能够说明∠A=∠A‘,那么就可以由“边角边”得出△ABC≌△A'B'C.
知1-导
感悟新知
将△ABC作平移、旋转和轴反射等变换,使BC的像B"C”与B'C'重合,并使点A的像A"与点A'在B'C'的两旁,△ABC在上述变换下的像为△
A"B"C",如图,由上述变换性质可知△ABC
≌△
A"B'C',则AB=A"B'=
A'B',AC=A"C'=A'C'.连接A'A".
知1-导
感悟新知
∵A'B'=A"B',A'C'=A"C',
∴∠1=∠2,∠3=∠4.从而∠1+∠3=∠2+∠4,
即
∠B'A'C'=∠B'A"C.
在∠A'B'C'和∠A"B'C'中,
A'B'=A"B',
∠B'A'C'=
∠B'A"C',A'C'=A"C',
∴△A'B'C'≌△
A"B'C'
(SAS).
∴△ABC
≌△
A'B'C'.
知1-讲
结
论
感悟新知
三边分别相等的两个三角形全等.
知1-讲
感悟新知
1.证明书写格式:在△ABC和△A'B'C'中
AB
=A'B,
∵
AC=A'C'',∴△ABC≌△A'B'C.
BC=B'C',
知1-讲
感悟新知
要点精析:
(1)全等的元素:三边.
(2)在判定两三角形全等的书写过程中,等号左边是全等号左边三角形的三边,等号右边是全等号右边三角形的三边,即前后顺序要保持一致.
(3)书写过程中的边及三角形的顶点前后顺序要对应.
知1-讲
感悟新知
3.三角形全等的判定方法:在两个三角形的六个元素中(三条边和三个角),可以判断两个三角形全等的组合有4个:"SSS,SAS,ASA,AAS";不能判定两个三角形全等的组合有2个:"AAA,SSA".
知1-讲
感悟新知
例
1
已知:如图,AB=CD,BC=DA.
求证:∠B=∠D.
证明
在△ABC和△CDA中,AB=CD,
BC=DA,
AC=CA(公共边),
∴△ABC≌△CDA(SSS).
∴∠B=∠D.
知1-讲
总
结
感悟新知
综合法:利用某些已经证明过的结论和性质及已知条件,推导出所要证明的结论成立的方法叫综合法,其思维特点是:由因索果,即从已知条件出发,利用已知的数学定理、性质和公式,推出结论,本书的证明基本上都是用综合法.
本题运用了综合法,根据条件用"SSS"可得到全等的三角形,从全等三角形出发可找到与结论有关的相等的角.
知1-练
感悟新知
C
1.下列三角形中,与如图所示的△ABC全等的是( )
2.如图,已知AB=AC,AE=AD,点B,D,E,C在同一条直线上,要利用“SSS”推理得出△ABE≌△ACD,还需要添加的一个条件可以是( )
A.BD=DE
B.BD=CE
C.DE=CE
D.以上都不对
知1-练
感悟新知
B
3.
如图所示,若AB=CD,AD=CB,∠B=25°,则∠D=________°.
知1-练
感悟新知
分析:如图所示,连接AC,因为AC=AC,AB=CD,AD=CB,所以△ABC≌△CDA,所以∠D=∠B=25°.
25
知2-导
感悟新知
知识点
全等三角形的判定(SSS)的应用
2
已知:如图,AC与BD相交于点O,且AB=DC,AC=DE求证:∠A=∠D.
例2
知2-讲
感悟新知
证明
连接BC.
在△ABC和△DCB中,
AB=DC,
BC=CB(公共边),
AC=DB,
∴△ABC≌△DCB(SSS).
∴∠A=∠D.
知2-讲
感悟新知
总
结
综合法:利用某些已经证明过的结论和性质及已知条件,推导出所要证明的结论成立的方法叫综合法,其思维特点是:由因索果,即从已知条件出发,利用已知的数学定理、性质和公式,推出结论.本书的证明基本上都是用综合法.
本题运用了综合法,根据条件用"SSS"可得到全等的三角形,从全等三角形出发可找到与结论有关的相等的角.
1.如图,AB=CD,BC=DA,E,F是AC上两点,且AE=CF,DE=BF,那么图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
知2-练
感悟新知
C
2.如图,在△ABC和△DCB中,AB
=
DC,AC
=
DB,AC与DB交于点M.则△ABC与△DCB
全等吗?请说明理由.
知2-练
感悟新知
分析:要想说明△ABC≌△DCB,因为AB
=
DC,AC
=
DB,观察图形,因为BC是两个三角形的公共边,根据“边边边”,可得△ABC≌△DCB.
知2-练
感悟新知
解:全等.
理由是:因为在△ABC和△DCB中,AB
=
DC,AC
=
DB,BC=CB
所以△ABC≌△DCB(SSS)
知识点
三角形的稳定性
知3-导
感悟新知
3
由“边边边”可知,只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
三角形的稳定性在生产和生活中有广泛的应用,如日常生活中的定位锁、房屋的人字梁屋
顶等都采用三角形结构,其道理就
是运用三角形的稳定性.
知3-讲
感悟新知
1.三角形的稳定性:只要三角形三边的长度确定,那么这三角形的形状和大小也就固定了,三角形的这个性质,叫作三角形的稳定性.
2.四边及四边以上的图形不具有稳定性,为保证其稳定,常在多边形中构造三角形.
注意:稳定性是三角形的特性,其他图形都不具有稳定性.
知3-讲
感悟新知
例
3
<探究题>要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架呢?六边形呢?n边形呢?
导引:若要多边形稳定,需将它变换成若干个三角形.先画出图形,结合图形分割三角形得出:四边形:1根,五边形:2根,六边形:3根,由类比推理可知,n边形:(n-3)根,如图所示.
知3-讲
感悟新知
解:四边形木架至少要再钉上1根,五边形木架:2根,六边形木架:3根,n边形木架:(n-3)根.
知3-讲
结
论
感悟新知
(1)本题运用了数形结合思想,使问题更直观、易懂,还运用了从特殊到一般的思想,由四边形、五边形、六边形类比出n边形,此题为一道规律探究题,通过观察图形,分析、归纳其中的规律.
(2)从特殊到一般的思想是一种重要的数学思想方法,其特点是通过对特殊现象的认识,利用归纳、类比、猜想、探索发现一般的规律,如一般性的结论、解决问题的方法等.
1.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?
答:____________.(填“稳定
性”或“不稳定性”)
知3-练
感悟新知
稳定性
2.不是利用三角形稳定性的是(
)
A.自行车的三角形车架
B.三角形房架
C.照相机的三角架
D.矩形门框的斜拉条
知3-练
感悟新知
C
课堂小结
用“边边边”判定三角形全等
1.证明三角形全等时,除了充分应用题目提供的条件外,还应仔细观察图形,充分挖掘题目图形中的隐含条件,如公共边.
2.
利用“边边边”判断三角形全等时,当所给相等的边不是要判定的三角形的边时,往往利用等式的性质,在相等线段两边加上或减去同一(相等)线段,转化为两个三角形的边.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
