沪科版七年级数学上册3.3二元一次方程组及其解法第2课时课件(20张PPT)
文档属性
| 名称 | 沪科版七年级数学上册3.3二元一次方程组及其解法第2课时课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览






文档简介
沪科版数学七年级(上)
第3章 一次方程与方程组
3.3 二元一次方程及其解法
第二课时 二元一次方程组的解法
(代入消元法)
问题1:什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
问题4:什么是二元一次方程组的解?
问题2:什么是二元一次方程组?
共含有两个未知数的两个一次方程所组成的一组方程叫做
二元一次方程组。
二元一次方程组中各个方程的公共解,叫做二元 一次方程组的解。
回顾与思考
适合一个二元一次方程的一组未知数的值,叫做二元一次方程的解.
问题3:什么是二元一次方程的解?
注意:二元一次方程有无穷多个解;二元一次方程组有且只有一组解。
1. 把下列方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)
(1)
(2)
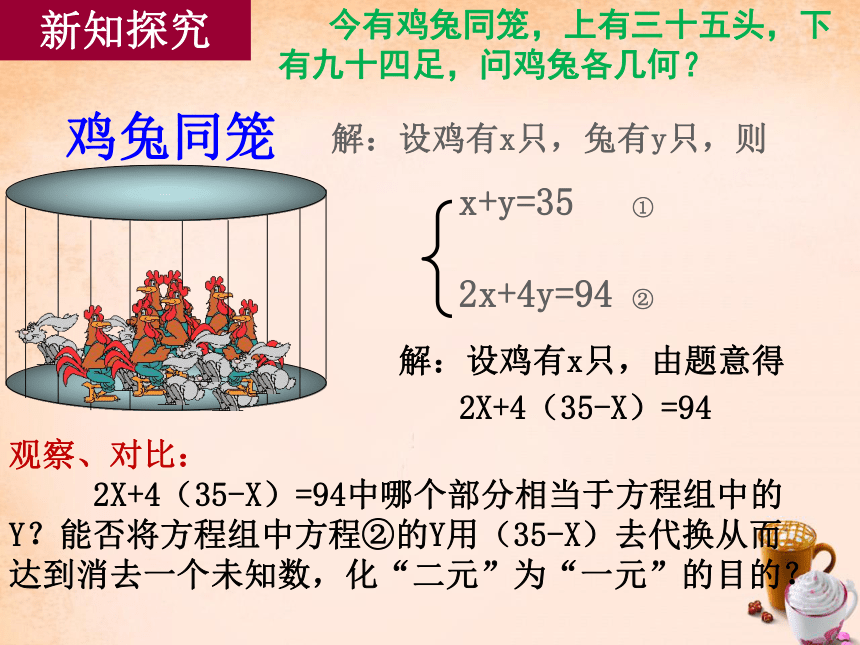
鸡兔同笼
解:设鸡有x只,兔有y只,则
x+y=35 ①
2x+4y=94 ②
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
新知探究
解:设鸡有x只,由题意得
2X+4(35-X)=94
观察、对比:
2X+4(35-X)=94中哪个部分相当于方程组中的Y?能否将方程组中方程②的Y用(35-X)去代换从而达到消去一个未知数,化“二元”为“一元”的目的?
.
.
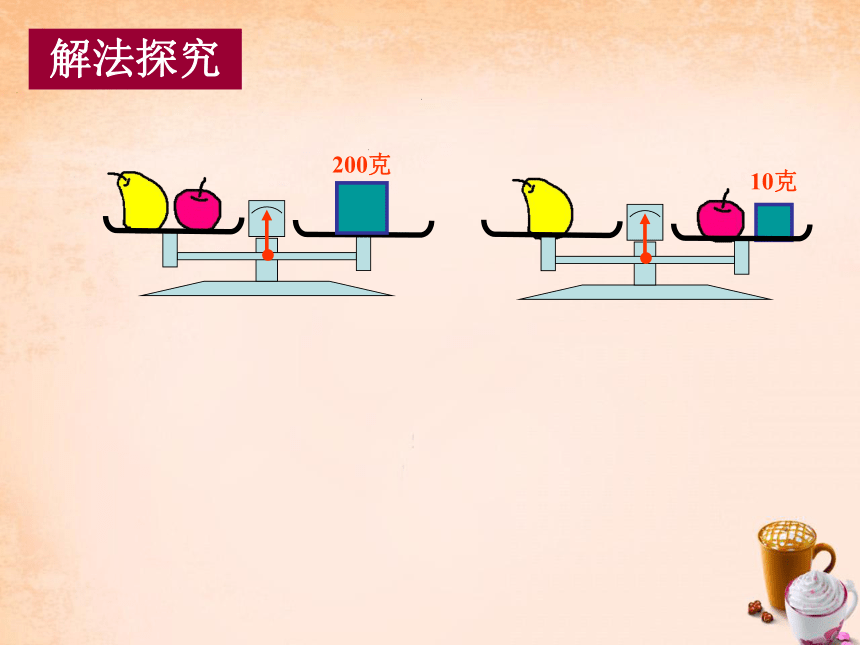
200克
10克
解法探究
y克
.
.
x克
200克
y克
x克
10克
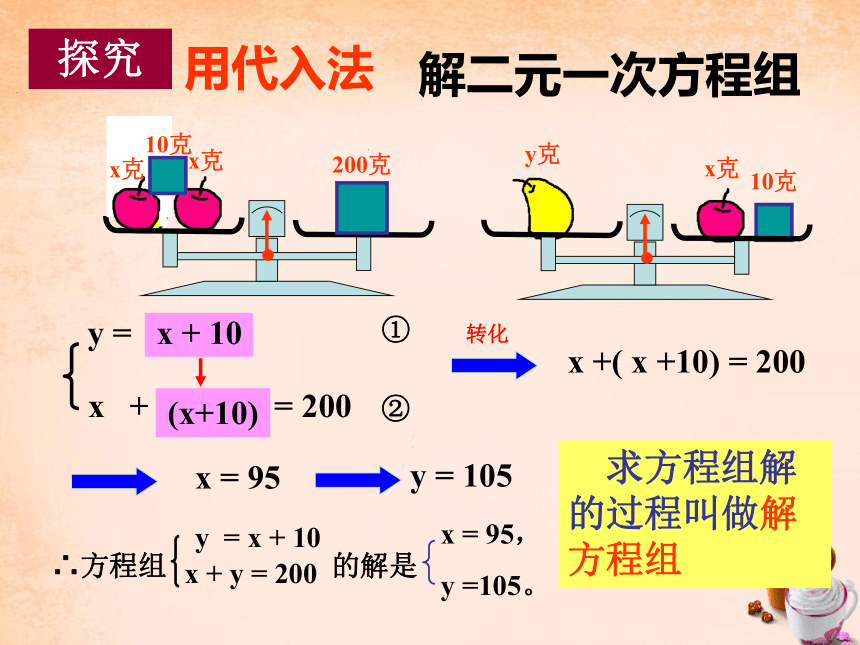
x + y = 200
y = x + 10
解二元一次方程组
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105。
求方程组解的过程叫做解方程组
转化
探究
把二元一次方程组转化为一元一次方程,体现了化归的思想。
二元一次方程组
一元一次方程
消 元
转化
解题思路:
将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,再代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
为了达到消元的目的,采用了代入的方法,这种解方程组的方法称为代入消元法,简称代入法。
将二元一次方程组中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,再代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这中解方程组方法叫做代入消元法,简称代入法。
代入消元法:
分析
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变:
2y – 3x = 1
x – y = – 1
①
②
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
谈谈思路
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 3+(-1)=2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法
用代入法解二元一次方程组
⑴
y=2x-3
3x+2y=8
⑵
2x- y=5
3x +4y=2
练一练
解:把② 代入①得,3x- 2(2x-3)= 8
解得,x= 2
把x = 2 代入②得 y=2×2-3, y= 1
∴原方程组的解为
x= 2
⑴
y=2x-3
3x-2y=8
②
①
y=1
记得检验:把x=2,y=-1代入方程①和②得,看看两个方程的左边是否都等于右边.
①
②
解:由①得,y=2x-5③
∴原方程组的解为
把③代入②得,3x+4(2x-5)=2
解得,x=2
把x=2代入③得,y=2×2-5,y=-1
⑵
2x- y=5
3x +4y=2
y=-1
x=2
谁的包裹多?
累死我了!
你还累?这么大的个,才比我多驮了2个。
哼!我从你背上拿来1个,我的包裹数就是你的2倍!
真的?!
它们各驮了多少包裹呢?
解决问题
由①得 x=2+y ③
把③代入②得 2+y+1=2(y-1)
解方程得 y=5
把y=4代入③ 得 x=7
方程组的解
解:设老牛驮了X个包裹,小马驮了Y个包裹.根据题意得到方程组:
X-Y=2
X+1=2(Y-1)
①
②
x=7
Y=5
答:老牛驮了7个包裹,小马驮了5个包裹
1、(2021·浙江丽水市·中考真题)解方程组:
.
2、(2021·浙江台州市·中考真题)解方程组:
中考真题练
用代入法解二元一次方程组
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2x+5y=21
x +3y=8
自 我 检 测
4、用代入消元法解下列方程
(1)
(2)
(3)
(4)
解二元一次方程组基本思路:
一般步骤:
变形技巧:
选择系数比较简单的方程进行变形。
课堂小结
一元一次方程
二元一次方程组
转化
消 元
变形
代入
求解
作答
用代入法解二元一次方程组的一般步骤
第3章 一次方程与方程组
3.3 二元一次方程及其解法
第二课时 二元一次方程组的解法
(代入消元法)
问题1:什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
问题4:什么是二元一次方程组的解?
问题2:什么是二元一次方程组?
共含有两个未知数的两个一次方程所组成的一组方程叫做
二元一次方程组。
二元一次方程组中各个方程的公共解,叫做二元 一次方程组的解。
回顾与思考
适合一个二元一次方程的一组未知数的值,叫做二元一次方程的解.
问题3:什么是二元一次方程的解?
注意:二元一次方程有无穷多个解;二元一次方程组有且只有一组解。
1. 把下列方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式?
(1)
(1)
(2)
鸡兔同笼
解:设鸡有x只,兔有y只,则
x+y=35 ①
2x+4y=94 ②
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
新知探究
解:设鸡有x只,由题意得
2X+4(35-X)=94
观察、对比:
2X+4(35-X)=94中哪个部分相当于方程组中的Y?能否将方程组中方程②的Y用(35-X)去代换从而达到消去一个未知数,化“二元”为“一元”的目的?
.
.
200克
10克
解法探究
y克
.
.
x克
200克
y克
x克
10克
x + y = 200
y = x + 10
解二元一次方程组
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105。
求方程组解的过程叫做解方程组
转化
探究
把二元一次方程组转化为一元一次方程,体现了化归的思想。
二元一次方程组
一元一次方程
消 元
转化
解题思路:
将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,再代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
为了达到消元的目的,采用了代入的方法,这种解方程组的方法称为代入消元法,简称代入法。
将二元一次方程组中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,再代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这中解方程组方法叫做代入消元法,简称代入法。
代入消元法:
分析
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变:
2y – 3x = 1
x – y = – 1
①
②
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
谈谈思路
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 3+(-1)=2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法
用代入法解二元一次方程组
⑴
y=2x-3
3x+2y=8
⑵
2x- y=5
3x +4y=2
练一练
解:把② 代入①得,3x- 2(2x-3)= 8
解得,x= 2
把x = 2 代入②得 y=2×2-3, y= 1
∴原方程组的解为
x= 2
⑴
y=2x-3
3x-2y=8
②
①
y=1
记得检验:把x=2,y=-1代入方程①和②得,看看两个方程的左边是否都等于右边.
①
②
解:由①得,y=2x-5③
∴原方程组的解为
把③代入②得,3x+4(2x-5)=2
解得,x=2
把x=2代入③得,y=2×2-5,y=-1
⑵
2x- y=5
3x +4y=2
y=-1
x=2
谁的包裹多?
累死我了!
你还累?这么大的个,才比我多驮了2个。
哼!我从你背上拿来1个,我的包裹数就是你的2倍!
真的?!
它们各驮了多少包裹呢?
解决问题
由①得 x=2+y ③
把③代入②得 2+y+1=2(y-1)
解方程得 y=5
把y=4代入③ 得 x=7
方程组的解
解:设老牛驮了X个包裹,小马驮了Y个包裹.根据题意得到方程组:
X-Y=2
X+1=2(Y-1)
①
②
x=7
Y=5
答:老牛驮了7个包裹,小马驮了5个包裹
1、(2021·浙江丽水市·中考真题)解方程组:
.
2、(2021·浙江台州市·中考真题)解方程组:
中考真题练
用代入法解二元一次方程组
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2x+5y=21
x +3y=8
自 我 检 测
4、用代入消元法解下列方程
(1)
(2)
(3)
(4)
解二元一次方程组基本思路:
一般步骤:
变形技巧:
选择系数比较简单的方程进行变形。
课堂小结
一元一次方程
二元一次方程组
转化
消 元
变形
代入
求解
作答
用代入法解二元一次方程组的一般步骤
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
