八年级《数据分析_众数_中位数》两节内容
文档属性
| 名称 | 八年级《数据分析_众数_中位数》两节内容 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-01 09:20:23 | ||
图片预览











文档简介
(共38张PPT)
学习目标:
1。了解加权平均数的概念,掌握加权平均数的计算方法
2.能合理地利用加权平均数进行数据处理和简单的应用
学习重点:
加权平均数在实际问题中的应用
学习难点:
如何从实际问题中获取信息,分析问题、解决问题、
日常生活中,我们常用平均数表示一组数据的“平均水平”
概念一:
一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)/n叫做这n个数的算术平均数,简称平均数。记为
问题 某市三个郊县的人数及人均耕地面积如下表:
郊县 人数/ 万 人均耕地面积/公顷
A 15 0.15
B 7 0.21
C 10 0.18
这个市郊县的人均耕地面积是多少 (精确到0.01公顷)
讨论
小明求得这个市郊县的人均耕地面积为 X=(0.15+0.21+0.18)/3=0.18(公颂).
你认为小明的做法有道理吗 为什么
(0.15×15+0.21×7+0.18×10)/(15+7+10) ≈0.17 (公颂).
问:0.15×15,0.21×7,0.18×10的意义是什么 15+7+10的意义是什么
概念二:
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时,往往给每个数据一个“权 ”(weight)。
如问题中的15就是0.15的权、7是0.21的权、10是0.18的权。而称(0.15×15+0.21×7+0.18×10)/(15+7+10)为0.15,0.21,0.18的 加权平均数 。
平均数0.17称为三个数0.15,0.21,0.18的加权平均数
15,7,10分别为三个数据的权
n个数x1,x2,…xn的权分别是w1,w2,…wn,则
(X1w1+x2w2+…+xnwn )/(w1+w2+…+wn)
叫做这n个数的加权平均数
加权平均数
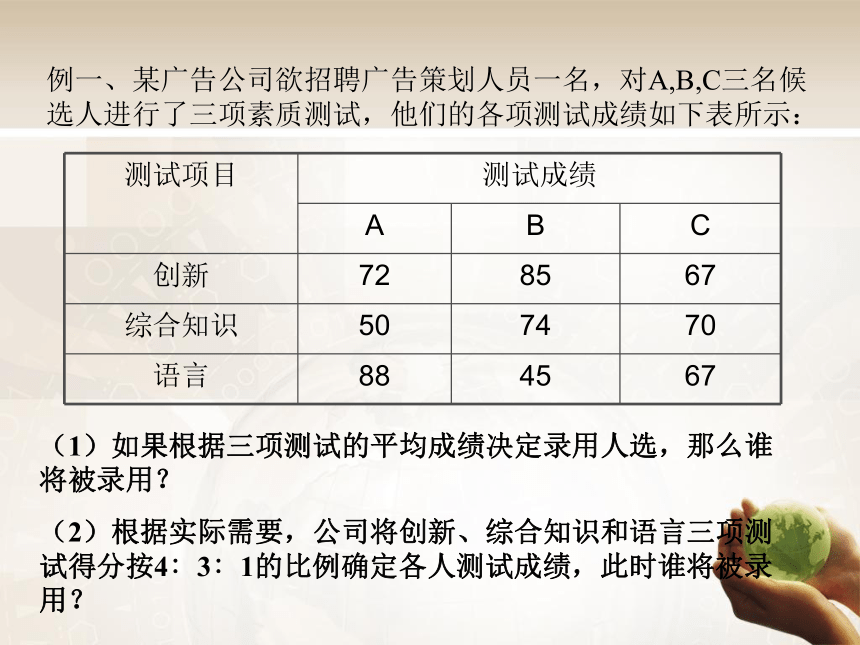
例一、某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用?
解:
(1)A的平均成绩为(72+50+88)/3=70分。
B的平均成绩为(85+74+45)/3=68分。
C的平均成绩为(67+70+67)/3=68分。
由70>68, 故A将被录用。
(2)根据题意, A的测试成绩为
(72×4+50×3+88×1)/(4+3+1)=65.75分。
B的测试成绩为(85×4+74×3+45×1)/(4+3+1)=75.875分。
C的测试成绩为(67×4+70×3+67×1)/(4+3+1)=68.125分。
因此候选人B将被录用
例2:一家公司打算招聘一名英文翻译,对甲乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
1)如果这有公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
解:1)听、说、读、写的成绩按照3:3:2:2的比确定,则甲的平均成绩为:85×3+83×3+78×2+75×2/3+3+2+2=81
乙的成绩为:73×3+80×3+85×2+82×2/3+3+2+2=79.3
显然甲的成绩比乙高,所以从成绩看,应该录取甲
2)听、说、读、写的成绩按照2:2:3:3的比确定,则甲的平均成绩为:
85×2+83×2+78×3+75×3/2+2+3+3=79.5
乙的成绩为:73×2+80×2+85×3+82×3/2+2+3+3=80.7
显然乙的成绩比甲高,所以从成绩看,应该录取乙
巩固练习
1、某班10名学生为支援希望工程,将平时积攒的零花钱捐献给贫困地区的失学儿童。每人捐款金额如下(单位:元):
10, 12, 13.5, 21, 40.8, 19.5, 20.8, 25, 16, 30。
这10名同学平均捐款多少元?
解:
这10名同学平均捐款为
(10+12+13.5+21+40.8+19.5+20.8+25+16+30) /10 = 20.86元
答:这10名同学平均捐款多少元。
2、某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动占成绩的20%,体育理论测试占30%,体育技能测试占50%。小颖的上述三项成绩依次为92分、80分、84分,则小颖这学期的体育成绩是多少?
解:
小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4分
答:小颖这学期的体育成绩是84.4分。
3、八年级一班有学生50人,二班有45人。期末数学测试成绩中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:
(50×81.5+45×83.4)/95=82.4(分)
答:两个班95名学生的平均分是82.4分。
延伸与提高
1、选择
(1)某次考试,5名学生的平均分是82,除甲外,其余4名 学生的平均分是80,那么甲的得分是
(A)84 (B) 86 (C) 88 (D) 90
( D )
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2 B:(x+y)/(m+n)
C:(mx+ny)/(x+y) D:(mx+ny)/(m+n)
( D )
3、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1 的平均数是
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
思考题:
一组6个数1,2,3,x, y, z 的平均数是 4
(1)求x, y, z 三数的平均数;
(2)求 4x+5, 4y+6, 4z+7 的平均数。
(1)解:由题意可得(1+2+3+x+y+z)/6=4
即 1+2+3+x+y+z=24
所以 x+y+z=18
所以 (x+y+z)/3=18/3=6
( C )
小结
概念一:
一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)/n叫做这n个数的算术平均数,简称平均数。记为
概念二:
n个数x1,x2,…xn的权分别是w1,w2,…wn,则
(X1w1+x2w2+…+xnwn )/(w1+w2+…+wn)
叫做这n个数的加权平均数
唐僧师徒取经后。。。。。。
第二天,猪八戒上班了。
八戒,我这里报酬不错, 月平均工资是2000元,你在这里好好干!
猴哥,你公司员工收入好不好?
职员C
职员D
我们好几个人工资都是1200元
我的工资是1500元,在公司算中等收入
八戒在公司工作了一周后
八戒,你先别激动嘛!平均工资确实是每月2000元,不信你看看公司的工资报表.
大师兄,你又骗我,我已问过其他员工,没有一个普通员工的工资超过2000的.
下表是“大圣鞋业”月工资报表:
请大家仔细观察表中的数据,公司员工月平均工资是多少 孙悟空是否欺骗了八戒
平均月工资能否客观地反映员工的实际收入
(3) 再仔细观察表中的数据,你认为用多少元钱反映一般员工的实际收入比较合适?
员工 总经理 副经理 员工A 员工B 员工C 员工D 员工E 员工F 学徒G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
不能,受到极值的影响
员工 总经理 副经理 员工A 员工B 员工C 员工D 员工E 员工F 学徒G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
月平均工资是指:
所有员工工资的平均数。
=2000
我没骗你吧, 月平均工资是2000元!
一组数据中出现次数最多的那个
数据叫做这组数据的众数.
一组数据按大小依次排列,把位于最中间的一个数据(当有偶数个数据时,为最中间两个数据的平均数)叫做这组数据的中位数。
员工 总工程师 工程师 技术元A 技术元B 技术元C 技术元D 技术元E 技术元F 见习技术元G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
中位数
众数
中位数:
众数:
1、数据1,3,4,2,4的中位数是_____
求中位数要先排序
这回又上了猴哥的当,不行,我得回去好好学习学习,充电去。
八戒充电
3
3.5
2和3
(众数不惟一)
2、数据1,3,4,5,2,6的中位数是_____
3、数据1,2,3,2,3,4的众数是_____
身高/米 1.5 1.6 1.65 1.7 1.75 1.8
人数/名 2 1 1 2 1 1
4、某班8名男同学的身高如下(单位:米)
试求出平均数、众数和中位数.
2.众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.一组数据中的众数可能不止一个,也可以没有.
1.求中位数时,要先将数据按大小顺序.排序时,从小到大或从大到小都可以.当数据个数为奇数时,中位数是最中间的一个数据;但当数据个数为偶数时,其中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等。
阶段性小结:
众数、中位数都是用来描述一组数据的集中趋势.
现在我的智商已经提高了,还是自己开店去!
1.八戒的鞋店在一段时间内销售了某种运动鞋30双,各种尺码的鞋的销售量如下:
假如你是八戒,你最关心哪一个统计量 你会如何进货
鞋的尺码/厘米 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
沙和尚凭着一股任劳任怨、塌实肯干的精神,当上了某家电公司的销售部经理,该部门有14名销售人员。
销售部14名销售人员,6月份销售业绩如下所示:
(1) 6月份销售额的平均数是_____,众数是_____,中位数是_____
(2)如果你是沙经理,为了调动员工的积极性,增加销售业绩,公司允许你采取“每月定额销售,超额有奖、完不成任务适当扣奖金”的措施,根据(1)的计算结果,你认为平均数、众数、中位数中的哪一个作为“定额”更恰当?
若以平均数630件作为定额,只有3人能完成,容易挫伤员工积极性;若是以众数460件作为定额,多数人轻易就能实现,应该把定额确定为中位数即480件更恰当.
沙经理的思考与决 策:
销售量/件 1500 1360 860 500 460 400
人数/名 1 1 1 4 5 2
480件
460件
630件
平均数是最常用的一个值,它能充分利用全部数据所提供的信息,但它容易受到极端值的影响.
2.中位数的优点计算简单,受极端值的影响较小,但不能充分利用所有数据的信息。
3.一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一个量,但各个数据的重复次数大致相等时,众数往往没有特别意义。
只要你有一双爱观察的眼睛、有一个爱思考的大脑,又有一颗爱创造的心相信你们会在生活中找到许许多多的数学知识,也会用数学知识把我们的生活变得更加美好!
学习目标:
1。了解加权平均数的概念,掌握加权平均数的计算方法
2.能合理地利用加权平均数进行数据处理和简单的应用
学习重点:
加权平均数在实际问题中的应用
学习难点:
如何从实际问题中获取信息,分析问题、解决问题、
日常生活中,我们常用平均数表示一组数据的“平均水平”
概念一:
一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)/n叫做这n个数的算术平均数,简称平均数。记为
问题 某市三个郊县的人数及人均耕地面积如下表:
郊县 人数/ 万 人均耕地面积/公顷
A 15 0.15
B 7 0.21
C 10 0.18
这个市郊县的人均耕地面积是多少 (精确到0.01公顷)
讨论
小明求得这个市郊县的人均耕地面积为 X=(0.15+0.21+0.18)/3=0.18(公颂).
你认为小明的做法有道理吗 为什么
(0.15×15+0.21×7+0.18×10)/(15+7+10) ≈0.17 (公颂).
问:0.15×15,0.21×7,0.18×10的意义是什么 15+7+10的意义是什么
概念二:
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时,往往给每个数据一个“权 ”(weight)。
如问题中的15就是0.15的权、7是0.21的权、10是0.18的权。而称(0.15×15+0.21×7+0.18×10)/(15+7+10)为0.15,0.21,0.18的 加权平均数 。
平均数0.17称为三个数0.15,0.21,0.18的加权平均数
15,7,10分别为三个数据的权
n个数x1,x2,…xn的权分别是w1,w2,…wn,则
(X1w1+x2w2+…+xnwn )/(w1+w2+…+wn)
叫做这n个数的加权平均数
加权平均数
例一、某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用?
解:
(1)A的平均成绩为(72+50+88)/3=70分。
B的平均成绩为(85+74+45)/3=68分。
C的平均成绩为(67+70+67)/3=68分。
由70>68, 故A将被录用。
(2)根据题意, A的测试成绩为
(72×4+50×3+88×1)/(4+3+1)=65.75分。
B的测试成绩为(85×4+74×3+45×1)/(4+3+1)=75.875分。
C的测试成绩为(67×4+70×3+67×1)/(4+3+1)=68.125分。
因此候选人B将被录用
例2:一家公司打算招聘一名英文翻译,对甲乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
1)如果这有公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
解:1)听、说、读、写的成绩按照3:3:2:2的比确定,则甲的平均成绩为:85×3+83×3+78×2+75×2/3+3+2+2=81
乙的成绩为:73×3+80×3+85×2+82×2/3+3+2+2=79.3
显然甲的成绩比乙高,所以从成绩看,应该录取甲
2)听、说、读、写的成绩按照2:2:3:3的比确定,则甲的平均成绩为:
85×2+83×2+78×3+75×3/2+2+3+3=79.5
乙的成绩为:73×2+80×2+85×3+82×3/2+2+3+3=80.7
显然乙的成绩比甲高,所以从成绩看,应该录取乙
巩固练习
1、某班10名学生为支援希望工程,将平时积攒的零花钱捐献给贫困地区的失学儿童。每人捐款金额如下(单位:元):
10, 12, 13.5, 21, 40.8, 19.5, 20.8, 25, 16, 30。
这10名同学平均捐款多少元?
解:
这10名同学平均捐款为
(10+12+13.5+21+40.8+19.5+20.8+25+16+30) /10 = 20.86元
答:这10名同学平均捐款多少元。
2、某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动占成绩的20%,体育理论测试占30%,体育技能测试占50%。小颖的上述三项成绩依次为92分、80分、84分,则小颖这学期的体育成绩是多少?
解:
小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4分
答:小颖这学期的体育成绩是84.4分。
3、八年级一班有学生50人,二班有45人。期末数学测试成绩中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:
(50×81.5+45×83.4)/95=82.4(分)
答:两个班95名学生的平均分是82.4分。
延伸与提高
1、选择
(1)某次考试,5名学生的平均分是82,除甲外,其余4名 学生的平均分是80,那么甲的得分是
(A)84 (B) 86 (C) 88 (D) 90
( D )
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2 B:(x+y)/(m+n)
C:(mx+ny)/(x+y) D:(mx+ny)/(m+n)
( D )
3、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1 的平均数是
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
思考题:
一组6个数1,2,3,x, y, z 的平均数是 4
(1)求x, y, z 三数的平均数;
(2)求 4x+5, 4y+6, 4z+7 的平均数。
(1)解:由题意可得(1+2+3+x+y+z)/6=4
即 1+2+3+x+y+z=24
所以 x+y+z=18
所以 (x+y+z)/3=18/3=6
( C )
小结
概念一:
一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)/n叫做这n个数的算术平均数,简称平均数。记为
概念二:
n个数x1,x2,…xn的权分别是w1,w2,…wn,则
(X1w1+x2w2+…+xnwn )/(w1+w2+…+wn)
叫做这n个数的加权平均数
唐僧师徒取经后。。。。。。
第二天,猪八戒上班了。
八戒,我这里报酬不错, 月平均工资是2000元,你在这里好好干!
猴哥,你公司员工收入好不好?
职员C
职员D
我们好几个人工资都是1200元
我的工资是1500元,在公司算中等收入
八戒在公司工作了一周后
八戒,你先别激动嘛!平均工资确实是每月2000元,不信你看看公司的工资报表.
大师兄,你又骗我,我已问过其他员工,没有一个普通员工的工资超过2000的.
下表是“大圣鞋业”月工资报表:
请大家仔细观察表中的数据,公司员工月平均工资是多少 孙悟空是否欺骗了八戒
平均月工资能否客观地反映员工的实际收入
(3) 再仔细观察表中的数据,你认为用多少元钱反映一般员工的实际收入比较合适?
员工 总经理 副经理 员工A 员工B 员工C 员工D 员工E 员工F 学徒G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
不能,受到极值的影响
员工 总经理 副经理 员工A 员工B 员工C 员工D 员工E 员工F 学徒G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
月平均工资是指:
所有员工工资的平均数。
=2000
我没骗你吧, 月平均工资是2000元!
一组数据中出现次数最多的那个
数据叫做这组数据的众数.
一组数据按大小依次排列,把位于最中间的一个数据(当有偶数个数据时,为最中间两个数据的平均数)叫做这组数据的中位数。
员工 总工程师 工程师 技术元A 技术元B 技术元C 技术元D 技术元E 技术元F 见习技术元G
工资 5000 4000 1800 1700 1500 1200 1200 1200 400
中位数
众数
中位数:
众数:
1、数据1,3,4,2,4的中位数是_____
求中位数要先排序
这回又上了猴哥的当,不行,我得回去好好学习学习,充电去。
八戒充电
3
3.5
2和3
(众数不惟一)
2、数据1,3,4,5,2,6的中位数是_____
3、数据1,2,3,2,3,4的众数是_____
身高/米 1.5 1.6 1.65 1.7 1.75 1.8
人数/名 2 1 1 2 1 1
4、某班8名男同学的身高如下(单位:米)
试求出平均数、众数和中位数.
2.众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.一组数据中的众数可能不止一个,也可以没有.
1.求中位数时,要先将数据按大小顺序.排序时,从小到大或从大到小都可以.当数据个数为奇数时,中位数是最中间的一个数据;但当数据个数为偶数时,其中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等。
阶段性小结:
众数、中位数都是用来描述一组数据的集中趋势.
现在我的智商已经提高了,还是自己开店去!
1.八戒的鞋店在一段时间内销售了某种运动鞋30双,各种尺码的鞋的销售量如下:
假如你是八戒,你最关心哪一个统计量 你会如何进货
鞋的尺码/厘米 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
沙和尚凭着一股任劳任怨、塌实肯干的精神,当上了某家电公司的销售部经理,该部门有14名销售人员。
销售部14名销售人员,6月份销售业绩如下所示:
(1) 6月份销售额的平均数是_____,众数是_____,中位数是_____
(2)如果你是沙经理,为了调动员工的积极性,增加销售业绩,公司允许你采取“每月定额销售,超额有奖、完不成任务适当扣奖金”的措施,根据(1)的计算结果,你认为平均数、众数、中位数中的哪一个作为“定额”更恰当?
若以平均数630件作为定额,只有3人能完成,容易挫伤员工积极性;若是以众数460件作为定额,多数人轻易就能实现,应该把定额确定为中位数即480件更恰当.
沙经理的思考与决 策:
销售量/件 1500 1360 860 500 460 400
人数/名 1 1 1 4 5 2
480件
460件
630件
平均数是最常用的一个值,它能充分利用全部数据所提供的信息,但它容易受到极端值的影响.
2.中位数的优点计算简单,受极端值的影响较小,但不能充分利用所有数据的信息。
3.一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一个量,但各个数据的重复次数大致相等时,众数往往没有特别意义。
只要你有一双爱观察的眼睛、有一个爱思考的大脑,又有一颗爱创造的心相信你们会在生活中找到许许多多的数学知识,也会用数学知识把我们的生活变得更加美好!
