10.5.1带电粒子在电场中的运动 课件(21张PPT)
文档属性
| 名称 | 10.5.1带电粒子在电场中的运动 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 334.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-11 22:03:29 | ||
图片预览





文档简介
重力与电场力共同作用下
的粒子运动问题
1、微观粒子(例如电子、质子)一般不考虑重力
2、宏观物体(例如带电小球、液滴)一般要考虑重力
3、带电微粒(题目没有明确说明是否考虑重力),要根据受力情况和运动情况来分析
判断是否考虑重力
1.平衡状态→合力为零,用三力平衡或正交分解法
2.匀变速直线运动→牛顿第二定律
3.类平抛运动→运动的合成与分解
分类讨论
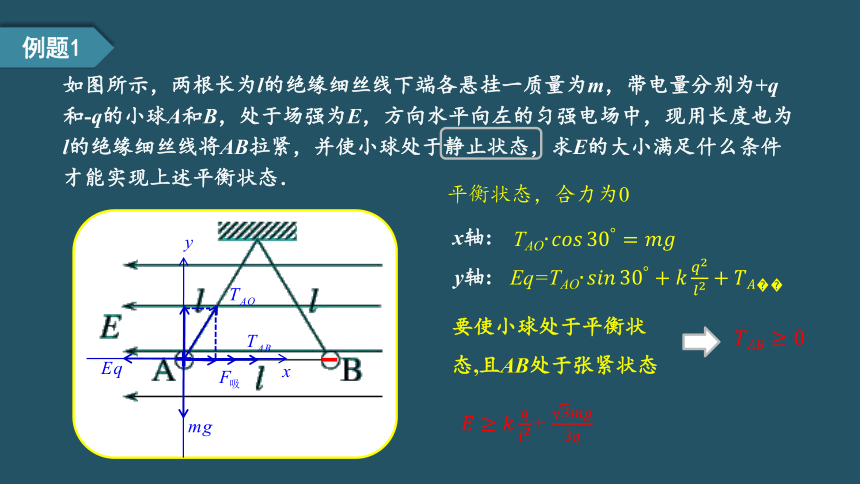
如图所示,两根长为l的绝缘细丝线下端各悬挂一质量为m,带电量分别为+q和-q的小球A和B,处于场强为E,方向水平向左的匀强电场中,现用长度也为l的绝缘细丝线将AB拉紧,并使小球处于静止状态,求E的大小满足什么条件才能实现上述平衡状态.
要使小球处于平衡状态,且AB处于张紧状态
x轴:
y轴:
平衡状态,合力为0
例题1
TAO?????????????30°=????????
?
Eq=TAO?????????????30°+????????2????2+??????????
?
????????????≥0
?
????≥????????????2+ 3????????3????
?
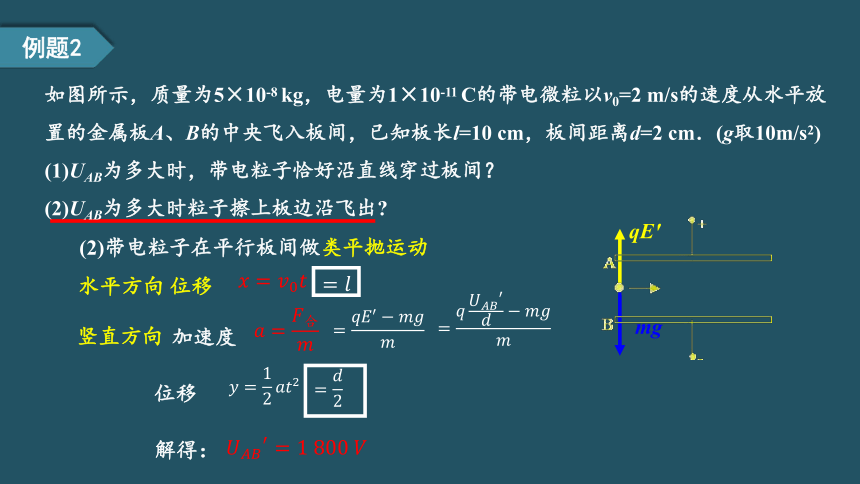
如图所示,质量为5×10-8 kg,电量为1×10-11 C的带电微粒以v0=2 m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长l=10 cm,板间距离d=2 cm.(g取10m/s2)
(1)UAB为多大时,带电粒子恰好沿直线穿过板间?
(2)UAB为多大时粒子擦上板边沿飞出?
带电微粒是否要考虑重力?
带电微粒受到的重力和电场力平衡,必须要考虑重力.
????????=????????
?
????=????????????????
?
????????????=????????????????=1000?????
?
(1)带电粒子重力和电场力大小相等
qE
mg
思考:
例题2
解析:
????=????合????
?
????????????′=1?800?????
?
qE′
mg
(2)带电粒子在平行板间做类平抛运动
水平方向 位移
????=????0????
?
竖直方向
????=12????????2
?
=????
?
=????2
?
位移
加速度
=????????′?????????????
?
=????????????????′?????????????????
?
解得:
如图所示,质量为5×10-8 kg,电量为1×10-11 C的带电微粒以v0=2 m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长l=10 cm,板间距离d=2 cm.(g取10m/s2)
(1)UAB为多大时,带电粒子恰好沿直线穿过板间?
(2)UAB为多大时粒子擦上板边沿飞出?
例题2
力的角度分析带电粒子的运动
E
F
F
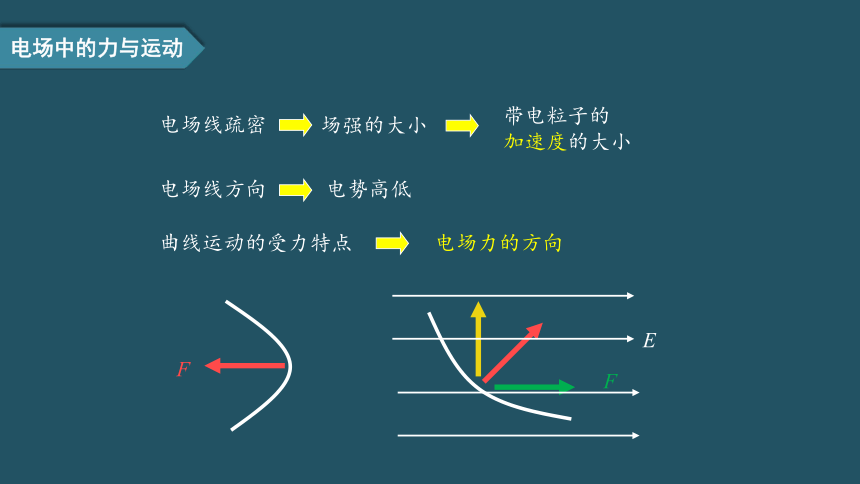
电场线疏密
场强的大小
带电粒子的 加速度的大小
电场线方向
电势高低
曲线运动的受力特点
电场力的方向
电场中的力与运动
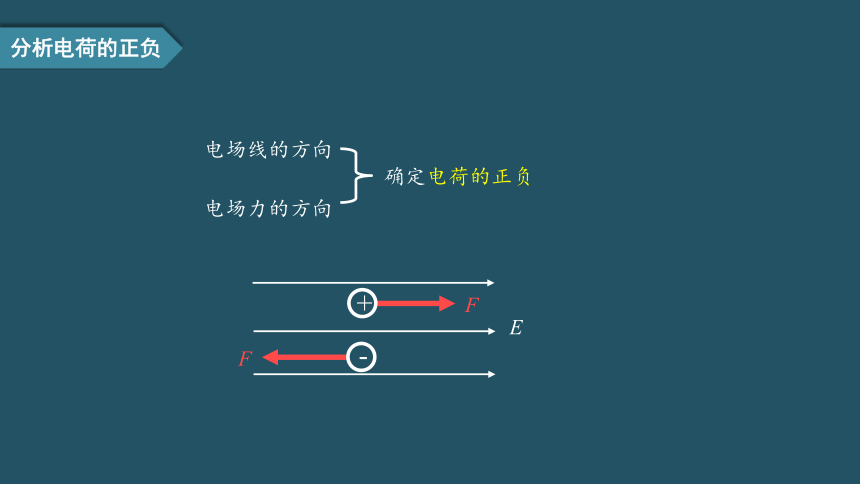
电场线的方向
电场力的方向
确定电荷的正负
E
F
+
F
-
分析电荷的正负
(多选)某电场的电场线的分布如图所示.一个带电粒子由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
A.粒子在N点的加速度大
B.粒子在N点的电势低
C.粒子带正电
D.粒子带负电
解析:电场线密的地方电场的强度大,所以粒子在N点的受力大,加速度大,故A正确;
沿电场线方向电势降低,所以N点电势低,B正确;
由图根据粒子的运动的轨迹可以知道,粒子受到的电场力的方向向上,而电场线的方向也向上,所以电荷为正电荷,故C正确、D错误.
例题 1
ABC
M
N
能量的角度分析带电粒子的运动
s
F
θ
电场力做正功
电势能减少
动能增大
s
F
θ
电场力做负功
电势能增大
动能减少
电场力的方向
位移的方向
确定电场力做功的正负
电势能的变化
动能的变化
电场中的功能关系
Q
A
B
如图所示,一带电粒子仅在电场力作用下,从A点运动到B点.比较A、B两点的物理量大小.请在下面空位填上 “>”、 “< ”或“ =”
场强 EA EB ;
加速度aA aB ;
电势 φA φB ;
运动电荷的电量q 0;
电场力做功W 0;
电势能 EpA EpB ;
动能 EkA EkB .
电场力F与位移s的夹角q是锐角,电场力做正功
电场力F与场强E的方向相反,粒子带负电
电场力做正功,电势能减少,动能增大
s
F
E
>
>
<
<
>
>
<
θ
电场中的运动轨迹问题
将一电荷量为+Q 的小球放在不带电的金属球附近, 所形成的电场线分布如图所示,金属球表面的电势处处相等 . a、b 为电场中的两点,则 ( )
A.a 点的电场强度比b 点的大
B.a 点的电势比b 点的高
C.检验电荷-q 在a 点的电势能比在b 点的大
D.将检验电荷-q 从a 点移到b 点的过程中,电场力做负功
F与s大致反向,电场力做负功
电场力做负功,电势能增加
F
ABD
S
例 题
重力场和电场的复合场中
的圆周运动
E
v0
mg
Eq
G’
O
→等效重力
+
复合场中的圆周运动
E
O
+
v0
mg
Eq
G’
→等效重力
复合场中的圆周运动
E
O
等效最高点
+
v0
mg
Eq
G’
→等效重力
E
O
+
v0
mg
Eq
G’
→等效重力
等效最高点→速度最小
等效最低点→速度最大
等效最低点
复合场中的圆周运动
E
O
+
v
mg
Eq
G '
→等效重力
等效最高点→速度最小
等效最低点→速度最大
临界条件
若小球刚好在圆轨道内侧做完整圆周运动,
求通过等效最高点的速度v
等效最高点弹力为0,由等效重力G'提供向心力
G ' =????????2+????????2 = m????2????
?
E
O
+
v
mg
Eq
G '
→等效重力
等效最高点→速度最小
等效最低点→速度最大
功能关系
若小球刚好做完整圆周运动,
求通过圆轨道底端的速度v0
对等效最高点到圆轨道底端列动能定理
W总 = 12 m????02 - 12 m????2
W总 = WG + WE
WG = mgR(1+cosθ)
WE = qE Rsinθ
?
v0
+
θ
再见
的粒子运动问题
1、微观粒子(例如电子、质子)一般不考虑重力
2、宏观物体(例如带电小球、液滴)一般要考虑重力
3、带电微粒(题目没有明确说明是否考虑重力),要根据受力情况和运动情况来分析
判断是否考虑重力
1.平衡状态→合力为零,用三力平衡或正交分解法
2.匀变速直线运动→牛顿第二定律
3.类平抛运动→运动的合成与分解
分类讨论
如图所示,两根长为l的绝缘细丝线下端各悬挂一质量为m,带电量分别为+q和-q的小球A和B,处于场强为E,方向水平向左的匀强电场中,现用长度也为l的绝缘细丝线将AB拉紧,并使小球处于静止状态,求E的大小满足什么条件才能实现上述平衡状态.
要使小球处于平衡状态,且AB处于张紧状态
x轴:
y轴:
平衡状态,合力为0
例题1
TAO?????????????30°=????????
?
Eq=TAO?????????????30°+????????2????2+??????????
?
????????????≥0
?
????≥????????????2+ 3????????3????
?
如图所示,质量为5×10-8 kg,电量为1×10-11 C的带电微粒以v0=2 m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长l=10 cm,板间距离d=2 cm.(g取10m/s2)
(1)UAB为多大时,带电粒子恰好沿直线穿过板间?
(2)UAB为多大时粒子擦上板边沿飞出?
带电微粒是否要考虑重力?
带电微粒受到的重力和电场力平衡,必须要考虑重力.
????????=????????
?
????=????????????????
?
????????????=????????????????=1000?????
?
(1)带电粒子重力和电场力大小相等
qE
mg
思考:
例题2
解析:
????=????合????
?
????????????′=1?800?????
?
qE′
mg
(2)带电粒子在平行板间做类平抛运动
水平方向 位移
????=????0????
?
竖直方向
????=12????????2
?
=????
?
=????2
?
位移
加速度
=????????′?????????????
?
=????????????????′?????????????????
?
解得:
如图所示,质量为5×10-8 kg,电量为1×10-11 C的带电微粒以v0=2 m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长l=10 cm,板间距离d=2 cm.(g取10m/s2)
(1)UAB为多大时,带电粒子恰好沿直线穿过板间?
(2)UAB为多大时粒子擦上板边沿飞出?
例题2
力的角度分析带电粒子的运动
E
F
F
电场线疏密
场强的大小
带电粒子的 加速度的大小
电场线方向
电势高低
曲线运动的受力特点
电场力的方向
电场中的力与运动
电场线的方向
电场力的方向
确定电荷的正负
E
F
+
F
-
分析电荷的正负
(多选)某电场的电场线的分布如图所示.一个带电粒子由M点沿图中虚线所示的途径运动通过N点.则下列判断正确的是( )
A.粒子在N点的加速度大
B.粒子在N点的电势低
C.粒子带正电
D.粒子带负电
解析:电场线密的地方电场的强度大,所以粒子在N点的受力大,加速度大,故A正确;
沿电场线方向电势降低,所以N点电势低,B正确;
由图根据粒子的运动的轨迹可以知道,粒子受到的电场力的方向向上,而电场线的方向也向上,所以电荷为正电荷,故C正确、D错误.
例题 1
ABC
M
N
能量的角度分析带电粒子的运动
s
F
θ
电场力做正功
电势能减少
动能增大
s
F
θ
电场力做负功
电势能增大
动能减少
电场力的方向
位移的方向
确定电场力做功的正负
电势能的变化
动能的变化
电场中的功能关系
Q
A
B
如图所示,一带电粒子仅在电场力作用下,从A点运动到B点.比较A、B两点的物理量大小.请在下面空位填上 “>”、 “< ”或“ =”
场强 EA EB ;
加速度aA aB ;
电势 φA φB ;
运动电荷的电量q 0;
电场力做功W 0;
电势能 EpA EpB ;
动能 EkA EkB .
电场力F与位移s的夹角q是锐角,电场力做正功
电场力F与场强E的方向相反,粒子带负电
电场力做正功,电势能减少,动能增大
s
F
E
>
>
<
<
>
>
<
θ
电场中的运动轨迹问题
将一电荷量为+Q 的小球放在不带电的金属球附近, 所形成的电场线分布如图所示,金属球表面的电势处处相等 . a、b 为电场中的两点,则 ( )
A.a 点的电场强度比b 点的大
B.a 点的电势比b 点的高
C.检验电荷-q 在a 点的电势能比在b 点的大
D.将检验电荷-q 从a 点移到b 点的过程中,电场力做负功
F与s大致反向,电场力做负功
电场力做负功,电势能增加
F
ABD
S
例 题
重力场和电场的复合场中
的圆周运动
E
v0
mg
Eq
G’
O
→等效重力
+
复合场中的圆周运动
E
O
+
v0
mg
Eq
G’
→等效重力
复合场中的圆周运动
E
O
等效最高点
+
v0
mg
Eq
G’
→等效重力
E
O
+
v0
mg
Eq
G’
→等效重力
等效最高点→速度最小
等效最低点→速度最大
等效最低点
复合场中的圆周运动
E
O
+
v
mg
Eq
G '
→等效重力
等效最高点→速度最小
等效最低点→速度最大
临界条件
若小球刚好在圆轨道内侧做完整圆周运动,
求通过等效最高点的速度v
等效最高点弹力为0,由等效重力G'提供向心力
G ' =????????2+????????2 = m????2????
?
E
O
+
v
mg
Eq
G '
→等效重力
等效最高点→速度最小
等效最低点→速度最大
功能关系
若小球刚好做完整圆周运动,
求通过圆轨道底端的速度v0
对等效最高点到圆轨道底端列动能定理
W总 = 12 m????02 - 12 m????2
W总 = WG + WE
WG = mgR(1+cosθ)
WE = qE Rsinθ
?
v0
+
θ
再见
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
