2021-2022学年人教版九年级数学上册 21.3 实际问题与一元二次方程 课件(第一课时 共25张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册 21.3 实际问题与一元二次方程 课件(第一课时 共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
实际问题与一元二次方程
第1课时
传播与增长率问题
人教版九年级数学上册
CONTENT
0
1
导入新课
0
2
新课学习
0
3
课堂练习
0
4
课堂小结
导入新课
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
PART
1
知识要点
1.传播问题
2.平均增长率(或降低率)问题
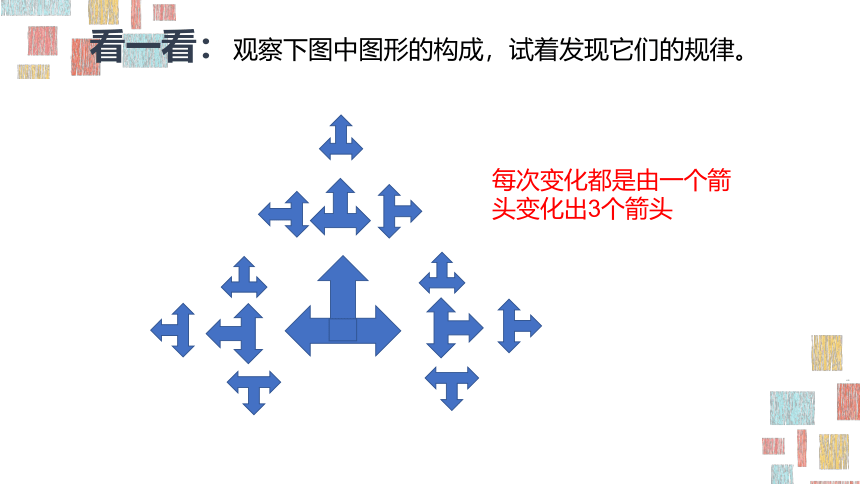
看一看:观察下图中图形的构成,试着发现它们的规律。
每次变化都是由一个箭头变化出3个箭头
新课学习
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
PART
2
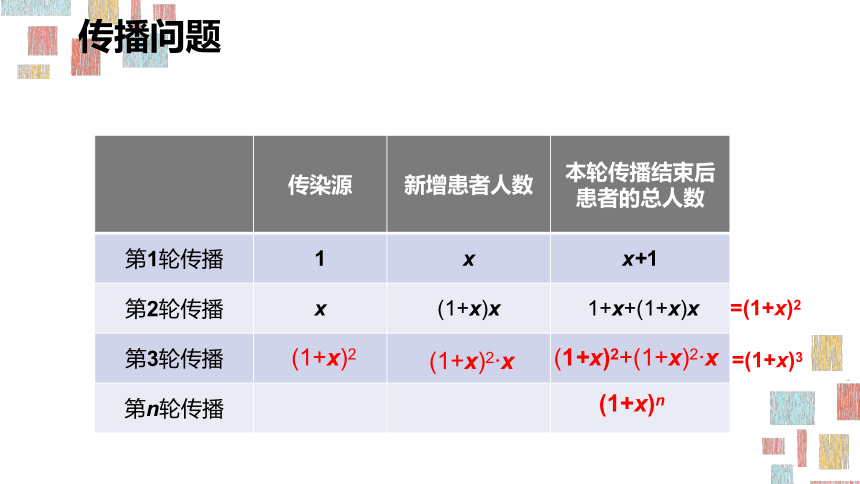
传播问题
问题1:有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
分析:设每轮传染中平均一个人传染了x个人,开始有一个人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_____人患了流感,第二轮传染中,这些人中的每一个人又传染了x个人,用代数式表示,第二轮后共有______________人患了流感.
[1+x+x(1+x)]
(1+x)
问题1:有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
解
每轮传染中平均一个人传染了x个人,
依题意,得
1+x+x(1+x)=121
x1=10,x2=-12(不合题意,舍去).
解方程,得
答
平均一个人传染了10个人.
传染源
新增患者人数
本轮传播结束后患者的总人数
第1轮传播
1
x
x+1
第2轮传播
x
(1+x)x
1+x+(1+x)x
第3轮传播
第n轮传播
=(1+x)2
(1+x)n
(1+x)2
(1+x)2?x
(1+x)2+(1+x)2?x
=(1+x)3
传播问题
传播问题规律:
(1)设开始数量为1,每轮感染的数量为x,经n轮感染后的数量为b,则所列方程为______________;
(2)设开始数量为a,每轮感染的数量为x,经n轮感染后的数量为b,则所列方程为_______________.
(1+x)n=b
a(1+x)n=b
传播问题
练一练:某校九年级学生毕业时,每个同学将自己的相片向全班其他同学各送一张作纪念,全班共送了2070张,如果全班有x名学生,根据题意列方程为(
)
A.x(x-1)=2070
B.x(x+1)=2070
C.2x(x+1)=2070
D.
=2070
A
练一练
平均增长率(或降低率)问题
问题1:两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
分析:甲种药品成本的年平均下降额为_______________________,乙种药品成本的年平均下降额为_______________________,乙种药品成本的年平均下降额较大。但是,年平均下降额不等同于年平均下降率(百分数)。
(5000-3000)÷2=1000(元)
(6000-3600)÷2=1200(元)
解
设甲种药品成本的年平均下降率为x.则一年后甲种药品成本为5000(1-x),两年后甲种药品成本为5000(1-x)2,根据题意,列方程,得
5000(1-x)2=3000
解方程,得
x1≈0.225,x2≈1.775.
答
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
平均增长率(或降低率)问题
平均增长率(或降低率)问题:
增长率的问题在实际生活中普遍存在,有一定的模式.若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为________________(其中增长取“+”,降低取“-”).
a(1±x)n=b
练一练:某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为x,则可列方程为(
)
A.80(1+x)2=100
B.100(1-x)2=80
C.80(1+2x)=100
D.80(1+x2)=100
A
课堂练习
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
PART
3
1.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为(
)
A.9人
B.10人
C.11人
D.12人
2.有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中平均一个人传染的人数为(
)
A.8人
B.9人
C.10人
D.11人
C
B
随堂练习
3.某市从2017年开始大力发展“竹文化”旅游产业,据统计,该市2017年“竹文化”旅游收入约为2亿元,预计2019年“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为(
)
A.2%
B.4.4%
C.20%
D.44%
C
随堂练习
4.政府近几年下大力气降低药品价格,希望使广大人民群众看得起病吃得起药.某种针剂的单价由100元经过两次降价,降至64元,则平均每次降低的百分率是(
)
A.36%
B.64%
C.20%
D.40%
C
随堂练习
5.教师节期间,某校数学组每个老师向本组其他老师各发一条祝福短信,据统计,全组共发出了210条祝福短信,则全组共有________名老师.
6.某养鸡场有一只患禽流感的小鸡,经过两天的传染后,养鸡场共169只小鸡患病.那么在每一天的传染中,平均一只小鸡传染了________只小鸡.
12
15
随堂练习
7.某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,若小分支、支干和主干的总数量是73,求每个支干长出的小分支数目.
答:每个支干长出8个小分支.
解
设每个支干长出x个小分支,依题意,得
1+x+x2=73,
解得x1=8,x2=-9(不合题意,舍去).
8.据报道,某省农作物秸秆的资源巨大,但合理利用量十分有限,2017年的利用率只有30%,大部分秸秆被直接焚烧了.假定该省每年产出的农作物秸秆总量不变,且合理利用量的增长率相同,要使2019年的利用率提高到60%,求每年的增长率.(取
≈1.41)
x1≈0.41=41%,x2≈-2.41(不合题意,舍去).
答:该省每年秸秆合理利用量的增长率约为41%.
解
设该省每年产出的农作物秸秆总量为1,合理利用量的增长率为x,
1×30%·(1+x)2=1×60%,
由题意,得
解得
课堂小结
PART
4
课堂小结
实际问题与一元二次方程解应题
传播问题
增长率问题
设开始数量为a,每轮感染的数量为x,经n轮感染后的数量为b,则所列方程为a(1+x)n=b.
若基数为a,平均增长率为x,则一次增长后的值为a(1+x),两次增长后的值为a(1+x)2.
若基数为a,平均降低率为x,则一次降低后的值为a(1-x),两次降低后的值为a(1-x)2.
课程结束
Summary
of
minimalist
work
授课老师:XXX
人教版九年级数学上册
实际问题与一元二次方程
第1课时
传播与增长率问题
人教版九年级数学上册
CONTENT
0
1
导入新课
0
2
新课学习
0
3
课堂练习
0
4
课堂小结
导入新课
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
PART
1
知识要点
1.传播问题
2.平均增长率(或降低率)问题
看一看:观察下图中图形的构成,试着发现它们的规律。
每次变化都是由一个箭头变化出3个箭头
新课学习
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
PART
2
传播问题
问题1:有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
分析:设每轮传染中平均一个人传染了x个人,开始有一个人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_____人患了流感,第二轮传染中,这些人中的每一个人又传染了x个人,用代数式表示,第二轮后共有______________人患了流感.
[1+x+x(1+x)]
(1+x)
问题1:有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
解
每轮传染中平均一个人传染了x个人,
依题意,得
1+x+x(1+x)=121
x1=10,x2=-12(不合题意,舍去).
解方程,得
答
平均一个人传染了10个人.
传染源
新增患者人数
本轮传播结束后患者的总人数
第1轮传播
1
x
x+1
第2轮传播
x
(1+x)x
1+x+(1+x)x
第3轮传播
第n轮传播
=(1+x)2
(1+x)n
(1+x)2
(1+x)2?x
(1+x)2+(1+x)2?x
=(1+x)3
传播问题
传播问题规律:
(1)设开始数量为1,每轮感染的数量为x,经n轮感染后的数量为b,则所列方程为______________;
(2)设开始数量为a,每轮感染的数量为x,经n轮感染后的数量为b,则所列方程为_______________.
(1+x)n=b
a(1+x)n=b
传播问题
练一练:某校九年级学生毕业时,每个同学将自己的相片向全班其他同学各送一张作纪念,全班共送了2070张,如果全班有x名学生,根据题意列方程为(
)
A.x(x-1)=2070
B.x(x+1)=2070
C.2x(x+1)=2070
D.
=2070
A
练一练
平均增长率(或降低率)问题
问题1:两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
分析:甲种药品成本的年平均下降额为_______________________,乙种药品成本的年平均下降额为_______________________,乙种药品成本的年平均下降额较大。但是,年平均下降额不等同于年平均下降率(百分数)。
(5000-3000)÷2=1000(元)
(6000-3600)÷2=1200(元)
解
设甲种药品成本的年平均下降率为x.则一年后甲种药品成本为5000(1-x),两年后甲种药品成本为5000(1-x)2,根据题意,列方程,得
5000(1-x)2=3000
解方程,得
x1≈0.225,x2≈1.775.
答
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
平均增长率(或降低率)问题
平均增长率(或降低率)问题:
增长率的问题在实际生活中普遍存在,有一定的模式.若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为________________(其中增长取“+”,降低取“-”).
a(1±x)n=b
练一练:某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为x,则可列方程为(
)
A.80(1+x)2=100
B.100(1-x)2=80
C.80(1+2x)=100
D.80(1+x2)=100
A
课堂练习
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
Lorem
ipsum
dolor
sit
amet,
consectetur
adipiscing
elit.
PART
3
1.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为(
)
A.9人
B.10人
C.11人
D.12人
2.有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中平均一个人传染的人数为(
)
A.8人
B.9人
C.10人
D.11人
C
B
随堂练习
3.某市从2017年开始大力发展“竹文化”旅游产业,据统计,该市2017年“竹文化”旅游收入约为2亿元,预计2019年“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为(
)
A.2%
B.4.4%
C.20%
D.44%
C
随堂练习
4.政府近几年下大力气降低药品价格,希望使广大人民群众看得起病吃得起药.某种针剂的单价由100元经过两次降价,降至64元,则平均每次降低的百分率是(
)
A.36%
B.64%
C.20%
D.40%
C
随堂练习
5.教师节期间,某校数学组每个老师向本组其他老师各发一条祝福短信,据统计,全组共发出了210条祝福短信,则全组共有________名老师.
6.某养鸡场有一只患禽流感的小鸡,经过两天的传染后,养鸡场共169只小鸡患病.那么在每一天的传染中,平均一只小鸡传染了________只小鸡.
12
15
随堂练习
7.某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,若小分支、支干和主干的总数量是73,求每个支干长出的小分支数目.
答:每个支干长出8个小分支.
解
设每个支干长出x个小分支,依题意,得
1+x+x2=73,
解得x1=8,x2=-9(不合题意,舍去).
8.据报道,某省农作物秸秆的资源巨大,但合理利用量十分有限,2017年的利用率只有30%,大部分秸秆被直接焚烧了.假定该省每年产出的农作物秸秆总量不变,且合理利用量的增长率相同,要使2019年的利用率提高到60%,求每年的增长率.(取
≈1.41)
x1≈0.41=41%,x2≈-2.41(不合题意,舍去).
答:该省每年秸秆合理利用量的增长率约为41%.
解
设该省每年产出的农作物秸秆总量为1,合理利用量的增长率为x,
1×30%·(1+x)2=1×60%,
由题意,得
解得
课堂小结
PART
4
课堂小结
实际问题与一元二次方程解应题
传播问题
增长率问题
设开始数量为a,每轮感染的数量为x,经n轮感染后的数量为b,则所列方程为a(1+x)n=b.
若基数为a,平均增长率为x,则一次增长后的值为a(1+x),两次增长后的值为a(1+x)2.
若基数为a,平均降低率为x,则一次降低后的值为a(1-x),两次降低后的值为a(1-x)2.
课程结束
Summary
of
minimalist
work
授课老师:XXX
人教版九年级数学上册
同课章节目录
