2021-2022学年人教版九年级数学上册《21.1 一元二次方程》课件(共16张)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册《21.1 一元二次方程》课件(共16张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 17:49:44 | ||
图片预览






文档简介
(共16张PPT)
21.1
一元二次方程
人教版
数学(初中)
(九年级
上)
第二十一章
一元二次方程
前
言
学习目标
1.理解一元二次方程的概念;
2.掌握一元二次方程的一般式,正确认识二次项系数、一次项系数及常数项.
3.
通过生活学习数学,并用数学解决生活中的常见问题。
重点难点
重点:一元二次方程的概念及其一般式。
难点:通过提出问题,建立一元二次方程的数学模型,再由一元一次方程的概念迁移到一元二次方程的概念。
只含有一个未知数(元),未知数次数都是1,等号两边都是整式,这样的方程叫一元一次方程。
一元一次方程的一般式:
(a,b为常数,
a≠0)
概念:
一元一次方程知识点回顾
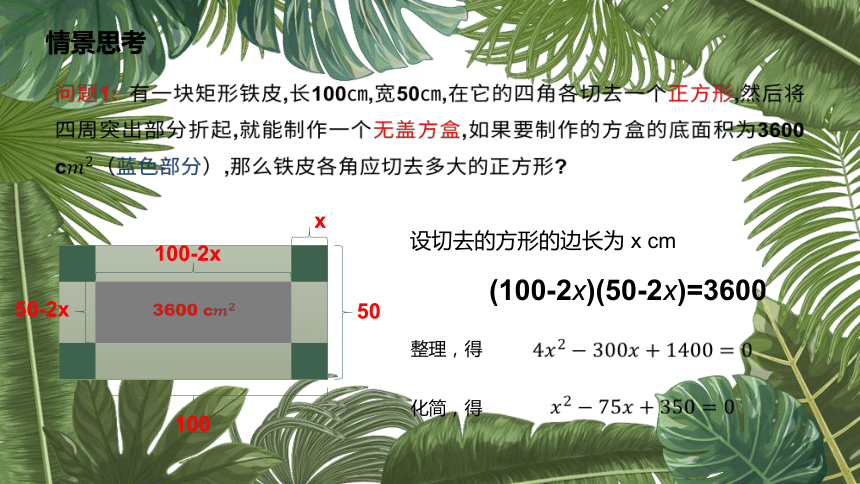
问题1:
有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600
c(蓝色部分),那么铁皮各角应切去多大的正方形?
50
100
3600
c
设切去的方形的边长为
x
cm
x
100-2x
50-2x
(100-2x)(50-2x)=3600
整理,得
化简,得
情景思考
问题2:正方形桌面的面积是
4
m2,求它的边长?
解:设正方形桌面的边长是
分析:正方形的面积=边长×边长
情景思考
解:设这个数为,得
问题3:一个数的平方是这个数的6倍,求这个数?
情景思考
观察下列各方程有什么共同点?
②只有一个未知数
③未知数最高次数是2
①等号两边都是整式
思考
只含有一个未知数(元),并且未知数最高次数是2,等号两边都是整式,这样的方程叫一元二次方程。
一元二次方程的一般式:ax
2
+
bx
+
c
=
0(a≠0)
概念:
二次项
一次项
常数项
二次项系数
一次项系数
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫一元二次方程的根。
一元二次方程
将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:
解:
解:
思考
一元二次方程
一般
形式
二次项
二次项
系数
一次项
一次项
系数
常数项
3x2=6x-1
(x+3)(x
-1)=6
5-7x2=0
课堂测试
1、判断下列方程中,哪些是一元二次方程?
(1)x2
+
-3=0
(2)x3-3x+4=0
(3)x2
-2y-3=0
(4)ax2+bx+c=0
(5)4x2+3x-2=(2x-1)2
分母中有未知数
最高项次数为3
有两个未知数
a可能为0
化简之后是一元一次方程
课堂测试
2.已知-2是关于x的一元二次方程的一个根,求c的值.
解:∵x=-2
∴
∴c=-10
课堂测试
3.一元二次方程(m+3)x?+3x+m?-9=0有一个根为0,则m的值为_____
分析:将x=0带入方程求得m=3或-3,而一元二次方程二次项系数不等于0,所以m=3
3
课堂测试
4.关于x的方程(2a
-
4)x2
-
2x+a=0,
(1)在什么条件下此方程为一元二次方程?
(2)在什么条件下此方程为一元一次方程?
提示:
方程
当
时,方程为一元二次方程。
当
时,方程变为bx+c=0,是一元一次方程。
课堂测试
5.a为何值时,方程为一元二次方程?
解:∵一元二次方程
∴
解得
∴
课堂测试
以-5、1、0三个数分别作为一个一元二次方程的系数和常数项,请尽可能多的写出满足条件的不同的一元二次方程?
小组讨论
21.1
一元二次方程
人教版
数学(初中)
(九年级
上)
第二十一章
一元二次方程
前
言
学习目标
1.理解一元二次方程的概念;
2.掌握一元二次方程的一般式,正确认识二次项系数、一次项系数及常数项.
3.
通过生活学习数学,并用数学解决生活中的常见问题。
重点难点
重点:一元二次方程的概念及其一般式。
难点:通过提出问题,建立一元二次方程的数学模型,再由一元一次方程的概念迁移到一元二次方程的概念。
只含有一个未知数(元),未知数次数都是1,等号两边都是整式,这样的方程叫一元一次方程。
一元一次方程的一般式:
(a,b为常数,
a≠0)
概念:
一元一次方程知识点回顾
问题1:
有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600
c(蓝色部分),那么铁皮各角应切去多大的正方形?
50
100
3600
c
设切去的方形的边长为
x
cm
x
100-2x
50-2x
(100-2x)(50-2x)=3600
整理,得
化简,得
情景思考
问题2:正方形桌面的面积是
4
m2,求它的边长?
解:设正方形桌面的边长是
分析:正方形的面积=边长×边长
情景思考
解:设这个数为,得
问题3:一个数的平方是这个数的6倍,求这个数?
情景思考
观察下列各方程有什么共同点?
②只有一个未知数
③未知数最高次数是2
①等号两边都是整式
思考
只含有一个未知数(元),并且未知数最高次数是2,等号两边都是整式,这样的方程叫一元二次方程。
一元二次方程的一般式:ax
2
+
bx
+
c
=
0(a≠0)
概念:
二次项
一次项
常数项
二次项系数
一次项系数
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫一元二次方程的根。
一元二次方程
将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:
解:
解:
思考
一元二次方程
一般
形式
二次项
二次项
系数
一次项
一次项
系数
常数项
3x2=6x-1
(x+3)(x
-1)=6
5-7x2=0
课堂测试
1、判断下列方程中,哪些是一元二次方程?
(1)x2
+
-3=0
(2)x3-3x+4=0
(3)x2
-2y-3=0
(4)ax2+bx+c=0
(5)4x2+3x-2=(2x-1)2
分母中有未知数
最高项次数为3
有两个未知数
a可能为0
化简之后是一元一次方程
课堂测试
2.已知-2是关于x的一元二次方程的一个根,求c的值.
解:∵x=-2
∴
∴c=-10
课堂测试
3.一元二次方程(m+3)x?+3x+m?-9=0有一个根为0,则m的值为_____
分析:将x=0带入方程求得m=3或-3,而一元二次方程二次项系数不等于0,所以m=3
3
课堂测试
4.关于x的方程(2a
-
4)x2
-
2x+a=0,
(1)在什么条件下此方程为一元二次方程?
(2)在什么条件下此方程为一元一次方程?
提示:
方程
当
时,方程为一元二次方程。
当
时,方程变为bx+c=0,是一元一次方程。
课堂测试
5.a为何值时,方程为一元二次方程?
解:∵一元二次方程
∴
解得
∴
课堂测试
以-5、1、0三个数分别作为一个一元二次方程的系数和常数项,请尽可能多的写出满足条件的不同的一元二次方程?
小组讨论
同课章节目录
