9.2.1总体取值规律的估计(知识储备+例题分析+课堂小练)-【新教材】人教A版(2019)高中数学必修第二册同步课堂讲义(Word含答案解析)
文档属性
| 名称 | 9.2.1总体取值规律的估计(知识储备+例题分析+课堂小练)-【新教材】人教A版(2019)高中数学必修第二册同步课堂讲义(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 74.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览


文档简介
2020-2021学年高一数学第二学期人教版(2019)必修第二册同步课堂
第九章 统计
3810532765知识储备
知识储备
9.2.1总体取值规律的估计
为了探索-组数据的取值规律,一般先要用表格对数据进行整理,或者用图将数据直观表示出来.在初中,我们曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数.
在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民用户占全市居民用户的比例,所以选择频率分布表和频率分布直方图来整理和表示数据.与画频数分布直方图类似,我们可以按以下步骤制作频率分布表、画频率分布直方图.
1.求极差
极差式一组数据中最大值与最小值的差
2.决定组距与组数
合适的组距与组数对发现数据分布规律有重要意义.组数太多或太少,都会影响我们了解数据的分布情况组距与组数的确定没有固定的标准,常常需要-一个尝试和选择的过?程。数据分组的组数与数据的个数有关,:一般数据的个数越多,所分组数也越多.
3.将数据分组
4.列频率分布表
5.画频率分布直方图
小长方形的面积=组距×false
-1524029845例题分析
例题分析
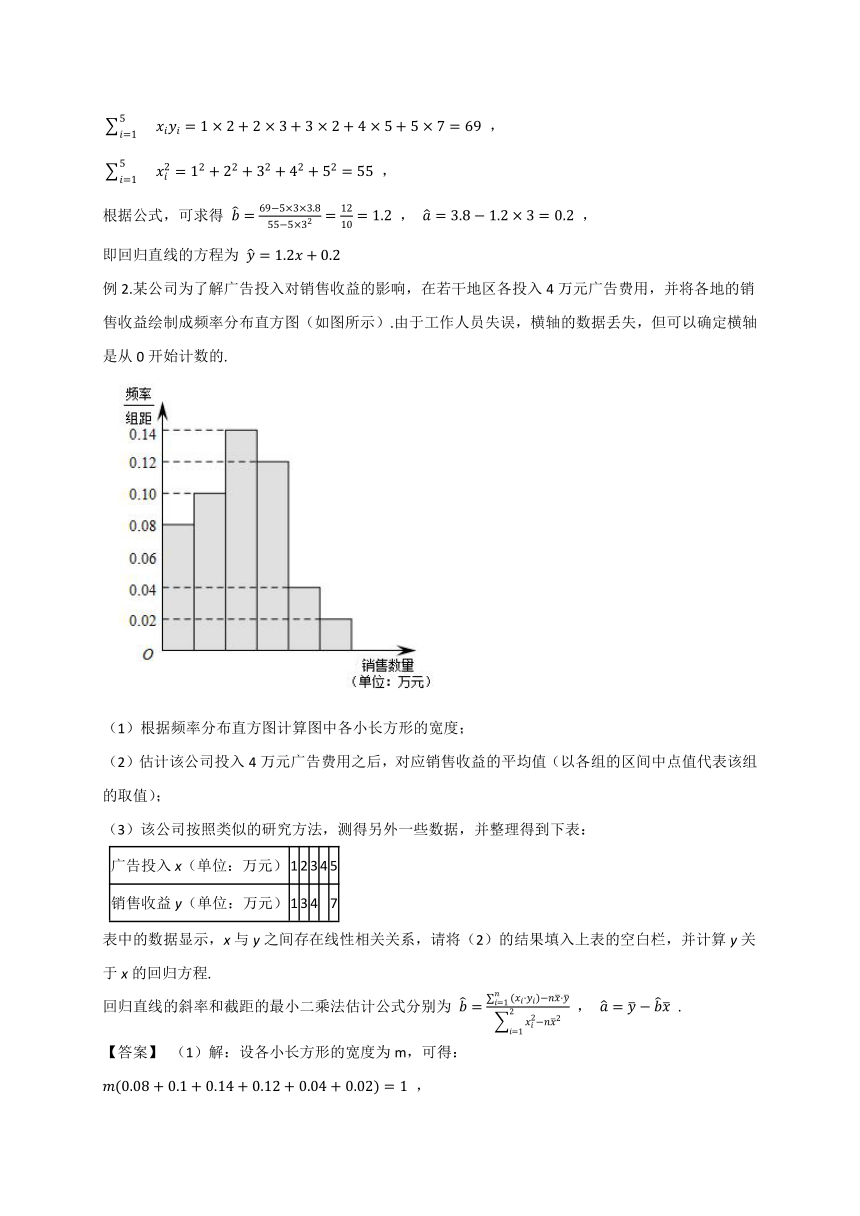
例1.某公司在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
附公式: b=i=1nxiyi?nxyi=1nxi2?nx2 , a=y?bx .
(1)根据频率分布直方图,计算图中各小长方形的宽度;
(2)根据频率分布直方图,估计投入4万元广告费用之后,销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 x (单位:万元)
1
2
3
4
5
销售收益 y (单位:百万元)
2
3
2
7
表中的数据显示, x 与 y 之间存在线性相关关系,请将(2)的结果填入空白栏,并计算 y 关于 x 的回归方程.
【答案】 (1)解:设各小长方形的宽度为 m ,由频率分布直方图各小长方形面积总和为1,可知 (0.08+0.1+0.14+0.12+0.04+0.02)?m=0.5m=1 ,故 m=2
(2)解:由(Ⅰ)知各小组依次是 [0,2),[2,4),[4,6),[6,8),[8,10),[10,12] ,
其中点分别为 1,3,5,7,9,11 ,对应的频率分别为 0.16,0.20,0.28,0.24,0.08,0.04 ,
故可估计平均值为 1×0.16+3×0.2+5×0.28+7×0.24+9×0.08+11×0.04=5
(3)解:由(2)知空白栏中填5.
由题意可知, x=1+2+3+4+55=3 , y=2+3+2+5+75=3.8 ,
i=15xiyi=1×2+2×3+3×2+4×5+5×7=69 ,
i=15xi2=12+22+32+42+52=55 ,
根据公式,可求得 b=69?5×3×3.855?5×32=1210=1.2 , a=3.8?1.2×3=0.2 ,
即回归直线的方程为 y=1.2x+0.2
例2.某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元)
1
2
3
4
5
销售收益y(单位:万元)
1
3
4
7
表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入上表的空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为 b=i=1n(xi?yi)?nx?yi=12xi2?nx2 , a=y?bx .
【答案】 (1)解:设各小长方形的宽度为m,可得:
m(0.08+0.1+0.14+0.12+0.04+0.02)=1 ,
∴m=2
(2)解:可得各组中点从左向右依次是1,3,5,7,9,11,
各组中点对应的频率从左向右依次是0.16,0.20,0.28,0.24,0.08,0.04,
∴ 平均值 =1×0.16+3×0.2+5×0.28+7×0.24+9×0.08+11×0.04=5
(3)解:得空白栏为5,
∴x=1+2+3+4+55=3 , y=1+3+4+5+75=4 ,
i=15xiyi=1×1+2×3+3×4+4×5+5×7=74 , i=15xi2=12+22+32+42+52=55 ,
根据公式可得 b=74?5×3×455?5×32=1.4 , a=4?1.4×3=?0.2 ,
故回归直线方程为 y=1.4x?0.2 .
-5715125095课堂小练
课堂小练
1.下列说法中,正确的是(?? )
A.?离散型随机变量的均值E(X)反映了X取值的概率平均值
B.?离散型随机变量的方差D(X)反映了X取值的平均水平
C.?离散型随机变量的均值E(X)反映了X取值的平均水平
D.?离散型随机变量的方差D(X)反映了X取值的概率平均值
2.在统计中,样本的标准差可以近似地反映总体数据的(???)
A.?平均状态????????????????????????B.?分布规律????????????????????????C.?离散程度????????????????????????D.?最大值和最小值
3.某村为了脱贫致富,引进了两种麻鸭品种,一种是旱养培育的品种,另一种是水养培育的品种.为了了解养殖两种麻鸭的经济效果情况,从中随机抽取500只麻鸭统计了它们一个季度的产蛋量(单位:个),制成了如图的频率分布直方图,且已知麻鸭的产蛋量在 [85,105] 的频率为0.66.
附: X?N(μ,σ2) ,则 P(μ?σK2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d .
P(K2≥k0)
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)求a,b的值;
(2)已知本次产蛋量近似服从 X~N(μ,σ2) (其中 μ 近似为样本平均数, σ2 似为样本方差).若本村约有10000只麻鸭,试估计产蛋量在110~120的麻鸭数量(以各组区间的中点值代表该组的取值).
(3)若以正常产蛋90个为标准,大于90个认为是良种,小于90个认为是次种.根据统计得出两种培育方法的 2×2 列联表如下,请完成表格中的统计数据,并判断是否有99.5%的把握认为产蛋量与培育方法有关.
良种
次种
总计
旱养培育
160
260
水养培育
60
总计
340
500
80010355600答案解析
答案解析
1.【答案】C
【解析】解:离散型随机变量X的均值反映了离散型随机变量取值的平均水平,故C正确,A错误; 随机变量的方差反映了随机变量取值偏离于均值的平均程度,故B、D错
故选C
2.【答案】 C
3.【答案】 (1)解:由频率分布直方图,可得产蛋量在 [85,105] 的频率为0.66,可得产蛋量在 [85,105] 的麻鸭数量为 500×0.66=330 (只).
所以产蛋量在 [75,85) 的麻鸭数量为 0.006×10×500=30 (只)
产蛋量在 [85,95) 的麻鸭数量为 0.024×10×500=120 (只)
产蛋量在 [115,125) 的麻鸭数量为 0.008×10×500=40 (只)
所以 a=(330?120)÷500÷10=0.042 , b=(500?330?30?40)÷500÷10=0.02 .
(2)解:由平均数的计算公式,可得:
μ=1500×(80×30+90×120+100×210+110×100+120×40)=100
σ2=1500×[30×(100?80)2+120×(100?90)2+210×(100?100)2+100×(100?110)2
+40×(100?120)2]=100 ,即 σ=10 ,
又由 P(110?P(100?10所以10000只麻鸭中估计产蛋量在110~120的麻鸭数量为 0.1359×10000=1359 (只)
(3)解:根据题意,得到 2×2 列联表:
良种
次种
总计
旱养培育
100
160
260
水养培育
60
180
240
总计
160
340
500
所以 K2=500×(100×180?60×160)2260×240×160×340≈10.393>7.879 ,
所以有99.5%的把握认为产蛋量与培育方法有关.
第九章 统计
3810532765知识储备
知识储备
9.2.1总体取值规律的估计
为了探索-组数据的取值规律,一般先要用表格对数据进行整理,或者用图将数据直观表示出来.在初中,我们曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数.
在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民用户占全市居民用户的比例,所以选择频率分布表和频率分布直方图来整理和表示数据.与画频数分布直方图类似,我们可以按以下步骤制作频率分布表、画频率分布直方图.
1.求极差
极差式一组数据中最大值与最小值的差
2.决定组距与组数
合适的组距与组数对发现数据分布规律有重要意义.组数太多或太少,都会影响我们了解数据的分布情况组距与组数的确定没有固定的标准,常常需要-一个尝试和选择的过?程。数据分组的组数与数据的个数有关,:一般数据的个数越多,所分组数也越多.
3.将数据分组
4.列频率分布表
5.画频率分布直方图
小长方形的面积=组距×false
-1524029845例题分析
例题分析
例1.某公司在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
附公式: b=i=1nxiyi?nxyi=1nxi2?nx2 , a=y?bx .
(1)根据频率分布直方图,计算图中各小长方形的宽度;
(2)根据频率分布直方图,估计投入4万元广告费用之后,销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 x (单位:万元)
1
2
3
4
5
销售收益 y (单位:百万元)
2
3
2
7
表中的数据显示, x 与 y 之间存在线性相关关系,请将(2)的结果填入空白栏,并计算 y 关于 x 的回归方程.
【答案】 (1)解:设各小长方形的宽度为 m ,由频率分布直方图各小长方形面积总和为1,可知 (0.08+0.1+0.14+0.12+0.04+0.02)?m=0.5m=1 ,故 m=2
(2)解:由(Ⅰ)知各小组依次是 [0,2),[2,4),[4,6),[6,8),[8,10),[10,12] ,
其中点分别为 1,3,5,7,9,11 ,对应的频率分别为 0.16,0.20,0.28,0.24,0.08,0.04 ,
故可估计平均值为 1×0.16+3×0.2+5×0.28+7×0.24+9×0.08+11×0.04=5
(3)解:由(2)知空白栏中填5.
由题意可知, x=1+2+3+4+55=3 , y=2+3+2+5+75=3.8 ,
i=15xiyi=1×2+2×3+3×2+4×5+5×7=69 ,
i=15xi2=12+22+32+42+52=55 ,
根据公式,可求得 b=69?5×3×3.855?5×32=1210=1.2 , a=3.8?1.2×3=0.2 ,
即回归直线的方程为 y=1.2x+0.2
例2.某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元)
1
2
3
4
5
销售收益y(单位:万元)
1
3
4
7
表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入上表的空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为 b=i=1n(xi?yi)?nx?yi=12xi2?nx2 , a=y?bx .
【答案】 (1)解:设各小长方形的宽度为m,可得:
m(0.08+0.1+0.14+0.12+0.04+0.02)=1 ,
∴m=2
(2)解:可得各组中点从左向右依次是1,3,5,7,9,11,
各组中点对应的频率从左向右依次是0.16,0.20,0.28,0.24,0.08,0.04,
∴ 平均值 =1×0.16+3×0.2+5×0.28+7×0.24+9×0.08+11×0.04=5
(3)解:得空白栏为5,
∴x=1+2+3+4+55=3 , y=1+3+4+5+75=4 ,
i=15xiyi=1×1+2×3+3×4+4×5+5×7=74 , i=15xi2=12+22+32+42+52=55 ,
根据公式可得 b=74?5×3×455?5×32=1.4 , a=4?1.4×3=?0.2 ,
故回归直线方程为 y=1.4x?0.2 .
-5715125095课堂小练
课堂小练
1.下列说法中,正确的是(?? )
A.?离散型随机变量的均值E(X)反映了X取值的概率平均值
B.?离散型随机变量的方差D(X)反映了X取值的平均水平
C.?离散型随机变量的均值E(X)反映了X取值的平均水平
D.?离散型随机变量的方差D(X)反映了X取值的概率平均值
2.在统计中,样本的标准差可以近似地反映总体数据的(???)
A.?平均状态????????????????????????B.?分布规律????????????????????????C.?离散程度????????????????????????D.?最大值和最小值
3.某村为了脱贫致富,引进了两种麻鸭品种,一种是旱养培育的品种,另一种是水养培育的品种.为了了解养殖两种麻鸭的经济效果情况,从中随机抽取500只麻鸭统计了它们一个季度的产蛋量(单位:个),制成了如图的频率分布直方图,且已知麻鸭的产蛋量在 [85,105] 的频率为0.66.
附: X?N(μ,σ2) ,则 P(μ?σ
P(K2≥k0)
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)求a,b的值;
(2)已知本次产蛋量近似服从 X~N(μ,σ2) (其中 μ 近似为样本平均数, σ2 似为样本方差).若本村约有10000只麻鸭,试估计产蛋量在110~120的麻鸭数量(以各组区间的中点值代表该组的取值).
(3)若以正常产蛋90个为标准,大于90个认为是良种,小于90个认为是次种.根据统计得出两种培育方法的 2×2 列联表如下,请完成表格中的统计数据,并判断是否有99.5%的把握认为产蛋量与培育方法有关.
良种
次种
总计
旱养培育
160
260
水养培育
60
总计
340
500
80010355600答案解析
答案解析
1.【答案】C
【解析】解:离散型随机变量X的均值反映了离散型随机变量取值的平均水平,故C正确,A错误; 随机变量的方差反映了随机变量取值偏离于均值的平均程度,故B、D错
故选C
2.【答案】 C
3.【答案】 (1)解:由频率分布直方图,可得产蛋量在 [85,105] 的频率为0.66,可得产蛋量在 [85,105] 的麻鸭数量为 500×0.66=330 (只).
所以产蛋量在 [75,85) 的麻鸭数量为 0.006×10×500=30 (只)
产蛋量在 [85,95) 的麻鸭数量为 0.024×10×500=120 (只)
产蛋量在 [115,125) 的麻鸭数量为 0.008×10×500=40 (只)
所以 a=(330?120)÷500÷10=0.042 , b=(500?330?30?40)÷500÷10=0.02 .
(2)解:由平均数的计算公式,可得:
μ=1500×(80×30+90×120+100×210+110×100+120×40)=100
σ2=1500×[30×(100?80)2+120×(100?90)2+210×(100?100)2+100×(100?110)2
+40×(100?120)2]=100 ,即 σ=10 ,
又由 P(110
(3)解:根据题意,得到 2×2 列联表:
良种
次种
总计
旱养培育
100
160
260
水养培育
60
180
240
总计
160
340
500
所以 K2=500×(100×180?60×160)2260×240×160×340≈10.393>7.879 ,
所以有99.5%的把握认为产蛋量与培育方法有关.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
