2020-2021学年华东师大版数学九年级上册 《22.2 一元二次方程解法(直接开平方法)》课件(共16张)
文档属性
| 名称 | 2020-2021学年华东师大版数学九年级上册 《22.2 一元二次方程解法(直接开平方法)》课件(共16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 575.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
潘新初级中学
一元二次方程的解法
直接开平方法
(第1课时)
合作学习 共同回顾
?
一个数x的平方等于p,这个数x叫做a的什么?
即 (p≥0)则x叫做a的平方根,表示为:
谁能说出下列方程的解?
1.
x2=49
2.
3x2=27
3.
x2+1=0
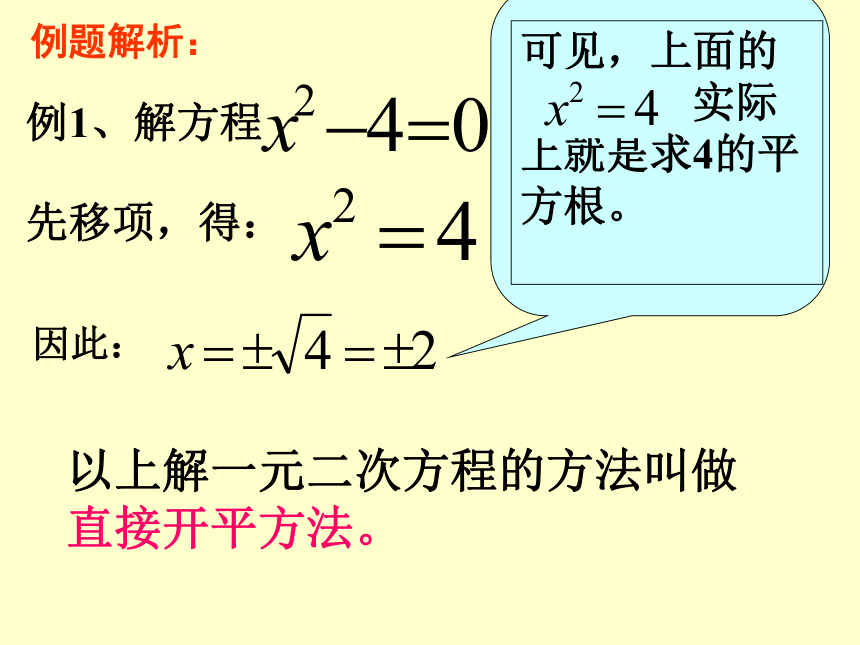
例1、解方程
先移项,得:
因此:
以上解一元二次方程的方法叫做直接开平方法。
例题解析:
可见,上面的
实际上就是求4的平方根。
典型例题
例1解下列方程
(1)x2-1.21=0
(2)4x2-1=0
解(1)移向,得x2=1.21
∴x=±1.1
即
x1=1.1,x2=-1.1
(2)移向,得4x2=1
两边都除以4,得
∴x=
即x1=
,x2=
x2=
将方程化成
(p≥0)的形式,再求解
牛刀小试:
解方程(同位之间每人一题)
1.
2x2-8=0
2.
9x2-5=3
典型例题
即x1=-1+
,x2=-1-
例2解下列方程:
⑴
(x+1)2=
2
⑵
(x-1)2-4
=
0
⑶
12(3-2x)2-3
=
0
分析:第1小题中只要将(x+1)看成是一个
整体,就可以运用直接开平方法求解;
解:(1)
(x+1)2=
2
∴x+1=
可以将方程化成
典型例题
分析:第2小题先将-4移到方程的右边,再同
第1小题一样地解;
例2解下列方程:
⑵
(x-1)2-4
=
0
⑶
12(3-2x)2-3
=
0
即x1=3,x2=-1
解:(2)移项,得(x-1)2=4
∴x-1=±2
x=1±2
典型例题
例2解下列方程:
⑶
12(3-2x)2-3
=
0
分析:第3小题先将-3移到方程的右边,再
两边都除以12,再同第1小题一样地去解,然后
两边都除以-2即可。
∴x1=
,
x2=
解:(3)移项,得12(3-2x)2=3
两边都除以12,得(3-2x)2=0.25
∴3-2x=±0.5
即3-2x=0.5,3-2x=-0.5
典型例题
例3.解方程(2x-1)2=(x-2)2
即x1=-1,x2=1
分析:如果把2x-1看成是(x-2)2的平方
根,同样可以用直接开平方法求解
解:2x-1=
即
2x-1=±(x-2)
∴2x-1=x-2或2x-1=-x+2
照葫芦画瓢:
解方程:同位左边做1,3右边2,4
1.
(x+6)2-9=0
2.
3(x-1)2-6=0
3.
x2-4x+4=5
4.
9x2+6x+1=4
用直接开平方法可解下列类型的一元二次方程:
根据平方根的定义,要特别注意:由于负数没有平方根,
所以,当p<0时,原方程无解。
学会自我总结
归纳
小结
(1)形如的
方程的解为
(2)形如的
方程的解为
潘新初级中学
一元二次方程的解法
直接开平方法
(第1课时)
合作学习 共同回顾
?
一个数x的平方等于p,这个数x叫做a的什么?
即 (p≥0)则x叫做a的平方根,表示为:
谁能说出下列方程的解?
1.
x2=49
2.
3x2=27
3.
x2+1=0
例1、解方程
先移项,得:
因此:
以上解一元二次方程的方法叫做直接开平方法。
例题解析:
可见,上面的
实际上就是求4的平方根。
典型例题
例1解下列方程
(1)x2-1.21=0
(2)4x2-1=0
解(1)移向,得x2=1.21
∴x=±1.1
即
x1=1.1,x2=-1.1
(2)移向,得4x2=1
两边都除以4,得
∴x=
即x1=
,x2=
x2=
将方程化成
(p≥0)的形式,再求解
牛刀小试:
解方程(同位之间每人一题)
1.
2x2-8=0
2.
9x2-5=3
典型例题
即x1=-1+
,x2=-1-
例2解下列方程:
⑴
(x+1)2=
2
⑵
(x-1)2-4
=
0
⑶
12(3-2x)2-3
=
0
分析:第1小题中只要将(x+1)看成是一个
整体,就可以运用直接开平方法求解;
解:(1)
(x+1)2=
2
∴x+1=
可以将方程化成
典型例题
分析:第2小题先将-4移到方程的右边,再同
第1小题一样地解;
例2解下列方程:
⑵
(x-1)2-4
=
0
⑶
12(3-2x)2-3
=
0
即x1=3,x2=-1
解:(2)移项,得(x-1)2=4
∴x-1=±2
x=1±2
典型例题
例2解下列方程:
⑶
12(3-2x)2-3
=
0
分析:第3小题先将-3移到方程的右边,再
两边都除以12,再同第1小题一样地去解,然后
两边都除以-2即可。
∴x1=
,
x2=
解:(3)移项,得12(3-2x)2=3
两边都除以12,得(3-2x)2=0.25
∴3-2x=±0.5
即3-2x=0.5,3-2x=-0.5
典型例题
例3.解方程(2x-1)2=(x-2)2
即x1=-1,x2=1
分析:如果把2x-1看成是(x-2)2的平方
根,同样可以用直接开平方法求解
解:2x-1=
即
2x-1=±(x-2)
∴2x-1=x-2或2x-1=-x+2
照葫芦画瓢:
解方程:同位左边做1,3右边2,4
1.
(x+6)2-9=0
2.
3(x-1)2-6=0
3.
x2-4x+4=5
4.
9x2+6x+1=4
用直接开平方法可解下列类型的一元二次方程:
根据平方根的定义,要特别注意:由于负数没有平方根,
所以,当p<0时,原方程无解。
学会自我总结
归纳
小结
(1)形如的
方程的解为
(2)形如的
方程的解为
