湖南省怀化市鹤城区2018-2019学年八年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 湖南省怀化市鹤城区2018-2019学年八年级上学期期末考试数学试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 328.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览


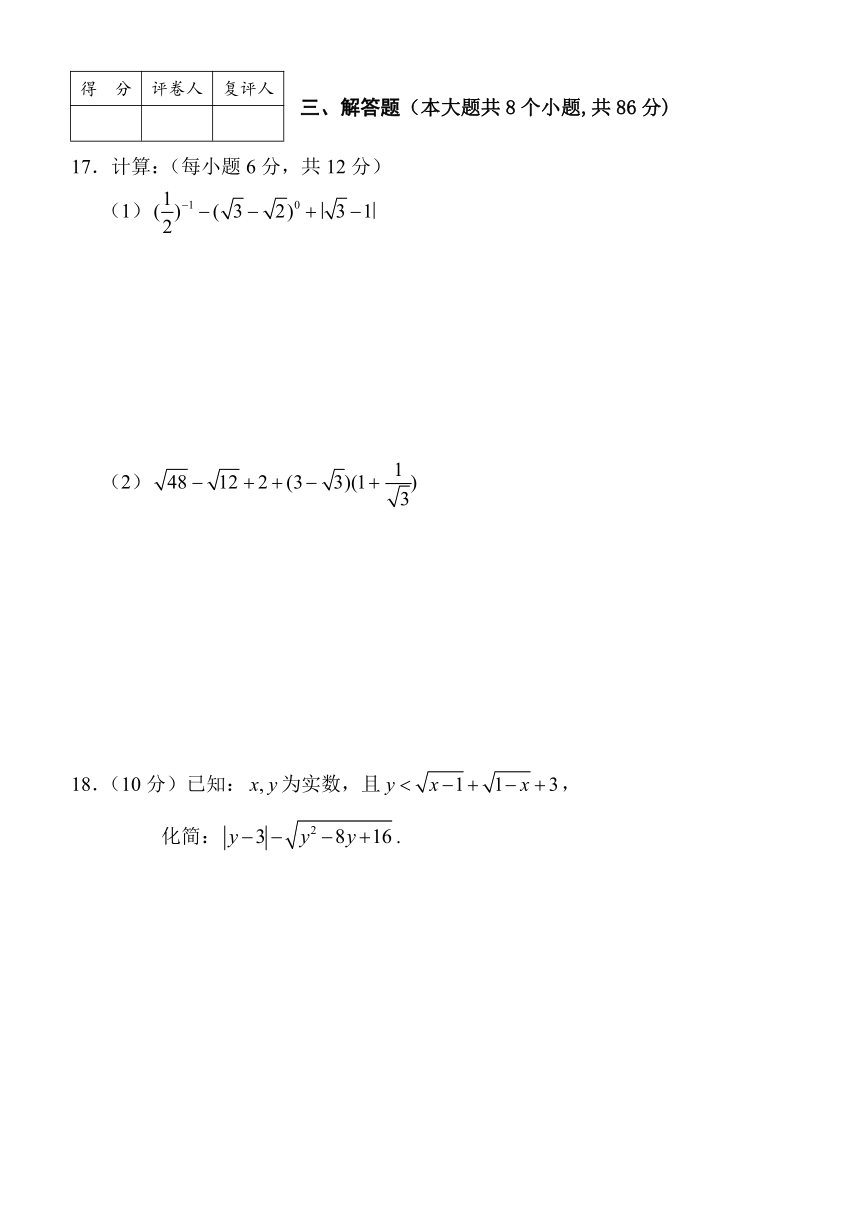
文档简介
怀化市鹤城区2018年下期期末教学质量检测
八年级数学
题
号
一
二
三
总
分
17
18
19
20
21
22
23
24
成
绩
满分
150分
时间
120分钟
得
分
评卷人
复评人
一、选择题:(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.下列代数式中,属于分式的是
A.
B.
C.
D.
2.下列各数为无理数的是
A.﹣2
B.0
C.
D.π
3.不等式组的所有整数解的和是
A.6
B.3
C.5
D.2
4.下列二次根式中,最简二次根式是
A.
B.
C.
D.
5.等腰三角形的两边长分别为1,,则这个三角形的周长为
A.2+
B.2+1
C.2+或2+1
D.以上都不对
6.
不等式的解集在数轴上表示为
A.
B.
C.
D.
7.若不等式的解集为,则的值为
A.
B.
C.
2
D.
4
8.△ABC中,∠C=90°,AD为∠BAC的角平分线,BD:DC=5:3,BC=32,则D到AB的距离为
A.12
B.16
C.20
D.24
9.如第9题图,若AB∥DE,BE=CF,下列条件中不能证明△ABF≌△DEC的是
A.AF=CD
B.AF∥CD
C.AB=DE
D.∠A=∠D
10.如第10题图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论共有
A.3个
B.4个
C.2个
D.1个
得
分
评卷人
复评人
二、填空题(共6小题,每小题4分,满分24分)
11.若最简二次根式与是同类二次根式,则=
.
12.
若代数式的值不大于代数式的值,那么的取值范围是
.
13.的算术平方根是
.
14.
计算:__________.
15.在中,与是同类二次根式的是
.
16.若与是同一个数的平方根,则的值为
.
得
分
评卷人
复评人
三、解答题(本大题共8个小题,共86分)
17.计算:(每小题6分,共12分)
(1)
(2)
18.(10分)已知:为实数,且,
化简:.
19.
(10分)
当时,求的值.
20.(10分)
解不等式组并将它的解集在数轴上表示出来.
21.
(10分)
已知满足,求的平方根.
22.(10分)如图,小明在A处看见前面山顶有个气象站,仰角为15°,当笔直向山脚方向前进了4千米到达B处时,小明看气象站的仰角为30°.你能算出这个气象站离地面的高度CD是多少千米吗?
23.(每小问6分,共12分)晨光文具店用进货款1620元购进A品牌的文具盒40个,B品牌的文具盒60个,其中A品牌文具盒的进货单价比B品牌文具盒的进货单价多3元.
(1)求A、B两种文具盒的进货单价.
(2)已知A品牌文具盒的售价为23元/个,若使这批文具盒全部售完后利润不低于500元,B品牌文具盒的销售单价最少是多少元?
24.(每小问4分,共12分)(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
求证:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
八年级数学参考答案
一、C
D
A
D
B
D
C
A
A
B
二、11.
a=3
12.
13.
3
14.
a-3
15.
16.
a=1
三、17(1)
(2)
18.
原式=-1
19.
当
原式=2
20.
21.
22.
2千米
23.(1)设A……为χ元/个
40χ+60(χ-3)=1620
χ=18
χ-3=15
(2)设B……为y元
(23-18)×40+60(y-15)≥500
y≥20
24.(1)证△ADB≌△CEA(AAS)
AE=BD
AD=CE
DE=AE+AD=BD+CE
(2)提示:先证∠DBA=∠CAE
再用AAS证△ADB≌CAE
(3)△DEF为等边三角形.
提示:先证明∠DBF=∠FAE
再证明:△DBF≌△EAF(SAS)
得:DF=EF,∠BFD=∠AFE.
∴∠DFE=∠DFA+∠AFE
=∠DFA
+∠BFD=60°
第10题图
第9题图
图1
图2
图3
PAGE
八年级数学
题
号
一
二
三
总
分
17
18
19
20
21
22
23
24
成
绩
满分
150分
时间
120分钟
得
分
评卷人
复评人
一、选择题:(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.下列代数式中,属于分式的是
A.
B.
C.
D.
2.下列各数为无理数的是
A.﹣2
B.0
C.
D.π
3.不等式组的所有整数解的和是
A.6
B.3
C.5
D.2
4.下列二次根式中,最简二次根式是
A.
B.
C.
D.
5.等腰三角形的两边长分别为1,,则这个三角形的周长为
A.2+
B.2+1
C.2+或2+1
D.以上都不对
6.
不等式的解集在数轴上表示为
A.
B.
C.
D.
7.若不等式的解集为,则的值为
A.
B.
C.
2
D.
4
8.△ABC中,∠C=90°,AD为∠BAC的角平分线,BD:DC=5:3,BC=32,则D到AB的距离为
A.12
B.16
C.20
D.24
9.如第9题图,若AB∥DE,BE=CF,下列条件中不能证明△ABF≌△DEC的是
A.AF=CD
B.AF∥CD
C.AB=DE
D.∠A=∠D
10.如第10题图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论共有
A.3个
B.4个
C.2个
D.1个
得
分
评卷人
复评人
二、填空题(共6小题,每小题4分,满分24分)
11.若最简二次根式与是同类二次根式,则=
.
12.
若代数式的值不大于代数式的值,那么的取值范围是
.
13.的算术平方根是
.
14.
计算:__________.
15.在中,与是同类二次根式的是
.
16.若与是同一个数的平方根,则的值为
.
得
分
评卷人
复评人
三、解答题(本大题共8个小题,共86分)
17.计算:(每小题6分,共12分)
(1)
(2)
18.(10分)已知:为实数,且,
化简:.
19.
(10分)
当时,求的值.
20.(10分)
解不等式组并将它的解集在数轴上表示出来.
21.
(10分)
已知满足,求的平方根.
22.(10分)如图,小明在A处看见前面山顶有个气象站,仰角为15°,当笔直向山脚方向前进了4千米到达B处时,小明看气象站的仰角为30°.你能算出这个气象站离地面的高度CD是多少千米吗?
23.(每小问6分,共12分)晨光文具店用进货款1620元购进A品牌的文具盒40个,B品牌的文具盒60个,其中A品牌文具盒的进货单价比B品牌文具盒的进货单价多3元.
(1)求A、B两种文具盒的进货单价.
(2)已知A品牌文具盒的售价为23元/个,若使这批文具盒全部售完后利润不低于500元,B品牌文具盒的销售单价最少是多少元?
24.(每小问4分,共12分)(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
求证:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
八年级数学参考答案
一、C
D
A
D
B
D
C
A
A
B
二、11.
a=3
12.
13.
3
14.
a-3
15.
16.
a=1
三、17(1)
(2)
18.
原式=-1
19.
当
原式=2
20.
21.
22.
2千米
23.(1)设A……为χ元/个
40χ+60(χ-3)=1620
χ=18
χ-3=15
(2)设B……为y元
(23-18)×40+60(y-15)≥500
y≥20
24.(1)证△ADB≌△CEA(AAS)
AE=BD
AD=CE
DE=AE+AD=BD+CE
(2)提示:先证∠DBA=∠CAE
再用AAS证△ADB≌CAE
(3)△DEF为等边三角形.
提示:先证明∠DBF=∠FAE
再证明:△DBF≌△EAF(SAS)
得:DF=EF,∠BFD=∠AFE.
∴∠DFE=∠DFA+∠AFE
=∠DFA
+∠BFD=60°
第10题图
第9题图
图1
图2
图3
PAGE
同课章节目录
