2021-2022学年鲁科版(2019)选择性必修第一册 4.3光的全反射 课后练习(word解析版)
文档属性
| 名称 | 2021-2022学年鲁科版(2019)选择性必修第一册 4.3光的全反射 课后练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览




文档简介
2021-2022学年鲁科版(2019)选择性必修第一册
4.3光的全反射 课后练习(解析版)
1.导光管采光系统是一套采集天然光,并经管道传输到室内的采光系统,如图为过装置中心轴线的截面。上面部分是收集阳光的半径为R的某种均匀透明材料的半球形采光球,O为球心,下面部分是内侧涂有反光涂层的导光管,MN为两部分的分界面,M、N为球面两点。若一束平行MN且与MN相距的细光束从空气入射到采光球表面时,经折射绿光恰好照射到N点。则( )
A.绿光在采光球中的传播速度为
B.红光一定能从N点上方射出
C.紫光有可能直接折射经过O点
D.要使光束在导光管中发生全反射,涂层折射率应小于管壁折射率
2.如图所示,a、b和c是三块平行玻璃砖,它们相互之间也平行,折射率大小,厚度之比。一束单色光从空气以入射角i射到a的上表面,在中光线的侧移量(入射光线与出射光线间的距离)分别为、、。下列说法正确的是( )
A.逐渐增大i,从c下表面射出的光线将消失
B.逐渐减小i,从c下表面射出的光线将消失
C.在i一定时,
D.在i一定时,
3.真空中一个直径足够大的圆柱形容器中有两层液体,上层液体厚为,折射率为,下层液体厚为,折射率为,已知。在容器底部中心有一单色点光源,可以向周围发出可见光。从光源发出的光,经折射以后达到上层液体表面的可见光的最大半径是( )
A. B. C. D.
4.如图是半径为R的半圆形玻璃砖,一束单色光从A点射入玻璃砖,在直径面上发生全反射,最终从B点射出玻璃砖(B点位置未标出),已知出射光与入射光之间互相垂直,真空中光速为c,则( )
A.玻璃砖的折射率为
B.光在玻璃砖内的速度为
C.光在玻璃砖中的临界角为
D.光在直径面上的全反射点P与O点的距离为
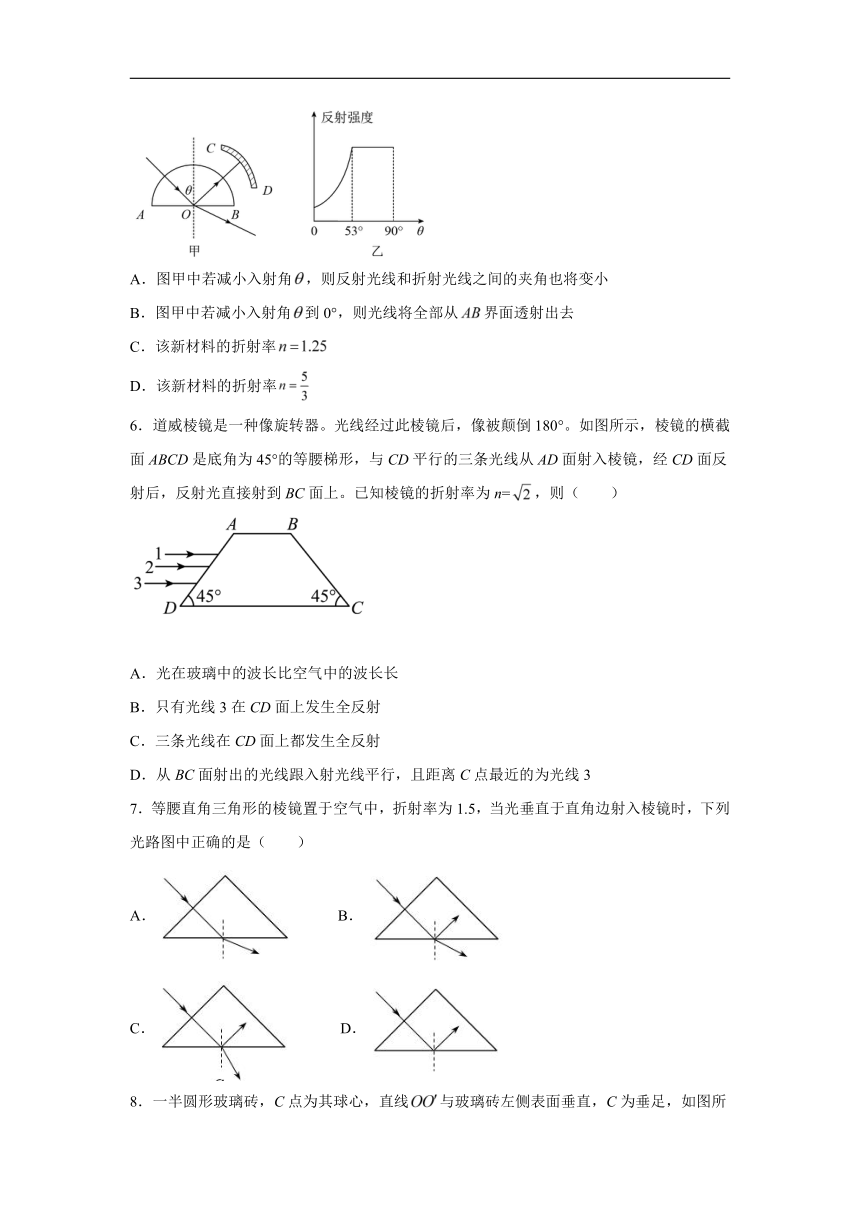
5.为了研究某种透明新材料的光学性质,将其压制成半圆柱形,如图甲所示。一束激光由真空沿半圆柱体的径向与其底面过O的法线成角射入。为光学传感器,可以探测光的强度。从面反射回来的光强随角变化的情况如图乙所示。则下列说法正确的是( )
A.图甲中若减小入射角,则反射光线和折射光线之间的夹角也将变小
B.图甲中若减小入射角到0°,则光线将全部从界面透射出去
C.该新材料的折射率
D.该新材料的折射率
6.道威棱镜是一种像旋转器。光线经过此棱镜后,像被颠倒180°。如图所示,棱镜的橫截面ABCD是底角为45°的等腰梯形,与CD平行的三条光线从AD面射入棱镜,经CD面反射后,反射光直接射到BC面上。已知棱镜的折射率为n=,则( )
A.光在玻璃中的波长比空气中的波长长
B.只有光线3在CD面上发生全反射
C.三条光线在CD面上都发生全反射
D.从BC面射出的光线跟入射光线平行,且距离C点最近的为光线3
7.等腰直角三角形的棱镜置于空气中,折射率为1.5,当光垂直于直角边射入棱镜时,下列光路图中正确的是( )
A. B.
C. D.
8.一半圆形玻璃砖,C点为其球心,直线与玻璃砖左侧表面垂直,C为垂足,如图所示。与直线平行且到直线距离相等的两条不同频率的细光束从空气射入玻璃砖,折射后相交于图中的P点,以下判断正确的是( )
A.a光的频率比b光的频率高
B.a光比b光在玻璃砖中传播速度大
C.在真空中a光的波长等于b光的波长
D.若a光、b光从玻璃砖中射入真空时,发生全反射时的临界角小于
9.如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合。一束白光沿着半圆柱形玻璃砖的半径从圆弧面垂直BD射到圆心O点上。使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动。在玻璃砖转动过程中,以下说法正确的是( )
A.在弧形屏上可以观察到反射光的色散现象
B.红光在玻璃砖中传播速度最小
C.折射光斑在弧形屏上沿顺时针方向移动
D.玻璃砖旋转过程中弧形屏上最先消失的一定是红光
10.如图所示为长方形玻璃砖一横截面ABQD,BQ边长为L,一束单色光从AB边上的P点进入玻璃砖,在AD边上的某点恰好发生全反射后从Q点射出。已知玻璃砖对这种单色光的折射率为n,光在真空中的传播速度为c,则单色光在玻璃砖中通过的时间为( )
A. B. C. D.
11.半径为R的半圆形玻璃砖置于水平桌面上,其截面如图所示,O为圆心,OA为其水平轴,PQ为直径上的两点,且,,两束相同的光线分别从P、Q两点垂直于直径射入,已知从P点射入的光线在圆弧面上恰好发生全反射,光在真空中的光速为c,下列判断正确的是( )
A.该玻璃砖的折射率为
B.由P点射入的光线进入玻璃砖后频率变为原来的
C.由Q点射入的光线在玻璃砖内(不考虑反射)运动的时间为
D.由Q点射入的光线的折射光线与OA的交点到圆心的距离为
12.方形透明容器充满某种透明液体,液体的深度,在容器底部中心有一个点状复色(两种颜色)激光光源,光源的大小可忽略不计,液面上形成的光斑俯视图如图所示,测得液面内部光斑a的直径,外部光环b的宽,下列说法正确的是( )
A.光斑a由两种色光组成,光环b由单色光形成
B.若仅将液体的深度h变大,则光斑的面积变大,光环宽度不变
C.液体对两种色光的折射率不同,较大者与较小者之比为
D.若光环b为单色光,这种光在液体中的传播速度比另一种色光的传播速度小
13.如图所示,水平桌面上有一折射率透明的玻璃半球,在球内有一离球心距离为的点光源S可向各个方向发光,点光源发出的所有光中刚好有一束光被反射回水平桌面。已知光在真空中的传播速度为,则由点光源S到反射回桌面的时间为( )
A.该束光在球形表面恰好发生全反射时的临界角为
B.该束光在球形表面恰好发生全反射时的临界角为
C.该束光由点光源S到反射回桌面的时间约为
D.该束光由点光源S到反射回桌面的时间约为
14.如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射入E点,并偏折到F点,已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则下列说法正确的是( )
A.该棱镜的折射率为 B.光在F点发生全反射
C.光从空气进入棱镜,波长变短 D.光从空气进入棱镜,波速变小
15.一透明介质的横截面为直角三角形,如图所示,一细束单色光从边上的点射入介质,经折射后的光线照到边的中点时恰好发生全反射。若,,,光在真空中传播的速度大小为,则( )
A.介质对该单色光的折射率为
B.介质对该单色光的折射率为
C.该单色光从点开始到第一次离开介质时所用的时间为
D.该单色光从点开始到第一次离开介质时所用的时间为
16.如图,ABC是横截面为直角三角形的玻璃三棱镜,一平行于CB边的细激光束从AC边上的某点射入棱镜后,在边上的D点部分反射、部分折射,其中反射光刚好与AC边平行。已知,,,空气中的光速为c。
①试通过计算,判断光束第一次射到BC边时是否发生全反射;
②求光束自进入棱镜到第一次从AC边射出所经历的时间。
17.如图所示,一种光学传感器是通过接收器Q接收到光的强度变化而触发工作的,光从挡风玻璃内侧Р点射向外侧M点再折射到空气中,测得入射角为,折射角为;光从Р点射向外侧N点,刚好发生全反射并被Q接收,已知挡风玻璃的厚度为d,光在空气中的传播速度为c,求:
①该挡风玻璃的折射率;
②光从P点射向外侧N点并被Q接收所需的时间。
18.如图,一个半径为R的圆形玻璃砖,为了测定该玻璃砖的折射率,将一条光线从玻璃砖上的A点射入,入射光线在过A点的横截面所在的平面内,玻璃砖横截面的圆心为O,在该横截面所在的平面内调节入射光线的方向,当圆形玻璃砖侧面上只有三处有光线射出时,测得入射光线与半径OA的夹角为,已知光在真空中传播的速度为。求:
(ⅰ)该玻璃砖的折射率;
(ⅱ)保持入射角不变,光线从射入玻璃砖到射出玻璃砖经历的最短时间。
19.如图所示,一个圆柱形油桶的底面直径为0.3m。当桶内没有油时,从A点经桶壁上边缘O点恰能看到桶壁上的B点。当桶内装满油时,仍沿方向看去,恰好看到桶壁上的C点。已知B点的深度为0.4m,间距为0.75m,真空中的光速。求:
(1)油的折射率;
(2)光在油中传播的速度。
20.某种透明材料制成的“n”形光学元件截面,内部半圆柱槽的半径为R,其他尺寸如图所示。一束激光(纸面内)从P点由空气中射入光学元件,入射角度,光束经折射后恰好与内圆柱面相切于Q点。已知P点在直径的延长线上,真空中的光速为c。
(1)求此材料对该激光的折射率n和该激光从P到Q经历的时间t;
(2)若仅改变人射光的人射角,使折射光线恰好在内圆柱面上发生全反射,求对应的入射角。
参考答案
1.B
【详解】
A.如图所示
根据几何关系
,
折射率
绿光在采光球中的传播速度为
故A错误;
B.红光折射率小,折射角大,则红光一定能从N点上方射出,故B正确;
C.紫光不可能直接折射经过O点,如果过的话,折射角为0°,故C错误;
D.光由光密到光疏可能发生全反射,则涂层折射率应大于管壁折射率,故D错误。
故选B。
2.D
【详解】
AB.光线在任一平行玻璃砖上面的折射角与下表面的入射角相等,根据光路可逆性,无论怎么增大或减小i都不会在玻璃砖下表面发生全反射,故A、B错误;
CD.在平行玻璃砖发生的侧移与玻璃砖的厚度成正比,随折射率的增大而增大,所以在一定时,,,故D正确,C错误。
故选D。
3.C
【详解】
如图当为全反射临界角时,光不会射出水面,即大于临界角时水面无可见光。因此等于临界角时射出的光为可见的最外部,临界角公式
根据折射定律
又
故
解得
所以最大半径为
故C正确。
故选C。
4.D
【详解】
A.如图,在A处
在P处的入射角
入射光与出射光相互垂直,m、L两法线垂直,
, ,
故A错误;
B.根据
故B错误;
C.临界角
故C错误;
D.如图 ,所以
故D正确。
故选D。
5.C
【详解】
A.甲中若减小入射角,根据折射定律和反射定律可知反射角和折射角都变小,则反射光线和折射光线之间的夹角将变大,故A错误;
B.减小入射角到0°时,不会发生折射现象,但是会有反射现象,所以光线不会全部从AB界面投射出去,故B错误;
CD.题图乙可知,当时发生全反射,则有
故C正确,D错误。
故选C。
6.C
【详解】
A.光的频率不变,波长与波速成正比,光从空气中射入玻璃中波速减小,则知光在玻璃中的波长比在空气中的波长小,故A错误;
BCD.作出如图所示光路图,设光线在棱镜中发生全反射的临界角为C,有
解得
C=45°
根据折射定律
解得
r=30°
由几何知识求得光线在CD面上的入射角θ=75°>45°,所以三条光线在CD面上都能发生全反射,且三条光线平行;由光路图可判断知距离C点最近的为光线1,故BD错误,C正确;
故选C。
7.D
【详解】
根据
得全反射临界角满足
光线射到三棱镜底边上的入射角为,因
其大于,所以光线在三棱镜底边上发生了全反射,没有折射光线,ABC错误,D正确。
故选D。
8.B
【详解】
A.由题分析可知,玻璃砖对b束光的折射率大于对a束光的折射率,则b光的频率高,故A错误;
B.由可知,由于玻璃砖对b束光的折射率大于对a束光的折射率,则a光比b光在玻璃砖中传播速度大,故B正确;
C.玻璃砖对b束光的折射率大于对a束光的折射率,则b光的频率高,由c=λf得知,在真空中,a光的波长大于b光的波长,故C错误;
D.由可知,a光的折射率小,则a光发生全反射的临界角大于b光,故D错误。
故选B。
9.C
【详解】
A.反射光线过圆心,射出时与圆形玻璃砖面垂直,不会发生色散现象,A错误;
B.根据光在玻璃中的传播的速度,红光频率最小,折射率最小,红光在玻璃砖中传播速度最大,B错误;
C.玻璃砖绕O点逆时针缓慢地转过角度θ的过程中,相当于玻璃砖不动,入射光线顺时针转动,折射光线随入射光线顺时针转动,折射光斑沿顺时针方向移动,C正确;
D.由临界角公式可知,紫光折射率最大,临界角最小,玻璃砖旋转过程中弧形屏上最先消失的一定是紫光,D错误。
故选C。
10.A
【详解】
根据折射率公式得
,
单色光在玻璃砖中通过的光程为
则单色光在玻璃砖中通过的时间为
故选A。
11.D
【详解】
A.由P点射入的光线在圆弧面上恰好发生全反射,由几何关系知
又因为
故
A错误;
B.由P点射入的光线进入玻璃砖后频率不变,B错误;
C.由几何关系可知,由Q点射入的光线在玻璃砖内运动的距离为
时间为
C错误;
D.设由Q点射入的光线在圆弧面上发生折射时的入射角和折射角分别为和,由折射定律知
设折射光线与水平轴OA的夹角为,由正弦定理得
由几何关系得
联立解得
D正确。
故选D。
12.AC
【详解】
A.液面形成光斑的原因是光在液体内部射向液面时发生了全反射,最边缘光线对应的入射角等于临界角,折射率小的光对应的临界角大,形成的光斑直径大;折射率大的光对应的临界角小,形成的光斑直径小,因为小光斑部分还有折射率小的色光,所以小光斑a是两种色光组成,光环b是单色光,A正确;
B.设光斑半径为r,边缘光线的光路如图所示
最大入射角为C等于全反射临界角,若h变大,C不变,则r变大,所以光斑面积变大,光环也变大,B错误;
C.根据几何关系可得折射率
由题知两个光亮的半径分别为15cm和21cm,液体深度为20cm,代入上式可求液体对两种色光的折射率之比为35:29,C正确;
D.由题知,b种色光在液面形成的光斑直径较大,对应的临界角较大,所以该种色光在液体中的折射率小,根据
可知该种色光在液体中传播的速度大, D错误。
故选AC。
13.AC
【详解】
AB.根据全反射的条件
解得
B错误A正确;
CD.光路如图,光源S发出的一条光线射到球面上的P点有
可得
即
对于位置已固定的光源,d与R都是定值,当 越大时,光线射出玻璃球的入射角α就越大,光线越容易发生全反射,点光源发出的所有光中刚好有一束发生全反射,即是当最大(θ=90°)时发生的全反射,如图所示
根据几何关系
根据
该束光由点光源S到反射回桌面的时间
解得
故选AC。
14.ACD
【详解】
A.在E点做出法线可知入射角为60°,折射角为30°,由
A正确;
B.由光路的可逆性可知,在BC边上的入射角小于临界角,不会发生全反射,B错误;
CD.由公式
可知,光从空气进入棱镜,波速变小,根据
光从空气进入棱镜,频率不变,波长变短,CD正确。
故选ACD。
15.AD
【详解】
AB.作出光路如图所示:
根据折射定律有
设光线到达BC边时发生全反射的临界角为,有
联立解得DE的长度为
介质对该单色光的折射率为
选项A正确,B错误;
CD.由可得
因为D为AC边的中点,E为边的中点,则DE∥AB,由几何关系可知,该光线在介质中传播的路程为
该光线在介质中的传播速度大小为
解得单色光从点开始到第一次离开介质时所用的时间
选项C错误,D正确。
故选AD。
16.①会发生全反射;②
【详解】
①设光在AC边的入射点为E,在BC边的反射点为F,在AC边的出射点为G,光路图图下图所示
由图结合题意可知,在D点的反射角为
为等边三角形,在E点折射时,入射角
折射角
根据折射定律
得
设发生全反射的临界角为C,则有
在F点,入射角为,因
故该处会发生全反射;
②光射至G点发生折射进入空气,由几何关系得
故光在棱镜中通过的路程
光在棱镜中的速度
由
联立解得
17.①;②
【详解】
①光线在M点发生折射,由于光线从光密介质射入光疏介质折射,则由折射定律得
②光在N点恰好发生全反射。则
即
光在介质中的传播速度为
光从点射向外侧点并被接收所需的时间
18.(ⅰ) ;(ⅱ)
【详解】
(ⅰ)根据对称性可知光在圆形玻璃砖内不会发生全反射,当圆形玻璃砖侧面上只有三处有光线射出时,三个光线出射点与圆心连线互成,作了光路图如图所示,三个出射点分别为B、C、A,则三角形ABC为等边三角形连接OA,即为折射角,根据几何关系可得
根据折射定律有
解得折射率
(ⅱ)通过分析可知光线第一次从B点射出时经历的时间最短,根据几何关系可得
光在玻璃砖里传播的速度为
则最短时间为
代入数据解得
19.(1)1.5;(2)
【详解】
(1)光路图如图所示
由几何关系可知:入射角与等大,折射角与等大
则
(2)由可得光在油中传播的速度为
20.(1),;(2)
【详解】
(1)光束经折射后恰好与内圆柱面相切于Q点,由题意可知,折射角为
根据
由几何关系可得
根据
从P到Q经历的时间
(2)如图所示
光束以入射角 由P点进入光学元件内折射到内圆面的C点,如果在C点发生全反射,则光束在球面上的入射角∠PCB等于临界角C
由正弦定理有
即
解得
根据
解得
4.3光的全反射 课后练习(解析版)
1.导光管采光系统是一套采集天然光,并经管道传输到室内的采光系统,如图为过装置中心轴线的截面。上面部分是收集阳光的半径为R的某种均匀透明材料的半球形采光球,O为球心,下面部分是内侧涂有反光涂层的导光管,MN为两部分的分界面,M、N为球面两点。若一束平行MN且与MN相距的细光束从空气入射到采光球表面时,经折射绿光恰好照射到N点。则( )
A.绿光在采光球中的传播速度为
B.红光一定能从N点上方射出
C.紫光有可能直接折射经过O点
D.要使光束在导光管中发生全反射,涂层折射率应小于管壁折射率
2.如图所示,a、b和c是三块平行玻璃砖,它们相互之间也平行,折射率大小,厚度之比。一束单色光从空气以入射角i射到a的上表面,在中光线的侧移量(入射光线与出射光线间的距离)分别为、、。下列说法正确的是( )
A.逐渐增大i,从c下表面射出的光线将消失
B.逐渐减小i,从c下表面射出的光线将消失
C.在i一定时,
D.在i一定时,
3.真空中一个直径足够大的圆柱形容器中有两层液体,上层液体厚为,折射率为,下层液体厚为,折射率为,已知。在容器底部中心有一单色点光源,可以向周围发出可见光。从光源发出的光,经折射以后达到上层液体表面的可见光的最大半径是( )
A. B. C. D.
4.如图是半径为R的半圆形玻璃砖,一束单色光从A点射入玻璃砖,在直径面上发生全反射,最终从B点射出玻璃砖(B点位置未标出),已知出射光与入射光之间互相垂直,真空中光速为c,则( )
A.玻璃砖的折射率为
B.光在玻璃砖内的速度为
C.光在玻璃砖中的临界角为
D.光在直径面上的全反射点P与O点的距离为
5.为了研究某种透明新材料的光学性质,将其压制成半圆柱形,如图甲所示。一束激光由真空沿半圆柱体的径向与其底面过O的法线成角射入。为光学传感器,可以探测光的强度。从面反射回来的光强随角变化的情况如图乙所示。则下列说法正确的是( )
A.图甲中若减小入射角,则反射光线和折射光线之间的夹角也将变小
B.图甲中若减小入射角到0°,则光线将全部从界面透射出去
C.该新材料的折射率
D.该新材料的折射率
6.道威棱镜是一种像旋转器。光线经过此棱镜后,像被颠倒180°。如图所示,棱镜的橫截面ABCD是底角为45°的等腰梯形,与CD平行的三条光线从AD面射入棱镜,经CD面反射后,反射光直接射到BC面上。已知棱镜的折射率为n=,则( )
A.光在玻璃中的波长比空气中的波长长
B.只有光线3在CD面上发生全反射
C.三条光线在CD面上都发生全反射
D.从BC面射出的光线跟入射光线平行,且距离C点最近的为光线3
7.等腰直角三角形的棱镜置于空气中,折射率为1.5,当光垂直于直角边射入棱镜时,下列光路图中正确的是( )
A. B.
C. D.
8.一半圆形玻璃砖,C点为其球心,直线与玻璃砖左侧表面垂直,C为垂足,如图所示。与直线平行且到直线距离相等的两条不同频率的细光束从空气射入玻璃砖,折射后相交于图中的P点,以下判断正确的是( )
A.a光的频率比b光的频率高
B.a光比b光在玻璃砖中传播速度大
C.在真空中a光的波长等于b光的波长
D.若a光、b光从玻璃砖中射入真空时,发生全反射时的临界角小于
9.如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合。一束白光沿着半圆柱形玻璃砖的半径从圆弧面垂直BD射到圆心O点上。使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动。在玻璃砖转动过程中,以下说法正确的是( )
A.在弧形屏上可以观察到反射光的色散现象
B.红光在玻璃砖中传播速度最小
C.折射光斑在弧形屏上沿顺时针方向移动
D.玻璃砖旋转过程中弧形屏上最先消失的一定是红光
10.如图所示为长方形玻璃砖一横截面ABQD,BQ边长为L,一束单色光从AB边上的P点进入玻璃砖,在AD边上的某点恰好发生全反射后从Q点射出。已知玻璃砖对这种单色光的折射率为n,光在真空中的传播速度为c,则单色光在玻璃砖中通过的时间为( )
A. B. C. D.
11.半径为R的半圆形玻璃砖置于水平桌面上,其截面如图所示,O为圆心,OA为其水平轴,PQ为直径上的两点,且,,两束相同的光线分别从P、Q两点垂直于直径射入,已知从P点射入的光线在圆弧面上恰好发生全反射,光在真空中的光速为c,下列判断正确的是( )
A.该玻璃砖的折射率为
B.由P点射入的光线进入玻璃砖后频率变为原来的
C.由Q点射入的光线在玻璃砖内(不考虑反射)运动的时间为
D.由Q点射入的光线的折射光线与OA的交点到圆心的距离为
12.方形透明容器充满某种透明液体,液体的深度,在容器底部中心有一个点状复色(两种颜色)激光光源,光源的大小可忽略不计,液面上形成的光斑俯视图如图所示,测得液面内部光斑a的直径,外部光环b的宽,下列说法正确的是( )
A.光斑a由两种色光组成,光环b由单色光形成
B.若仅将液体的深度h变大,则光斑的面积变大,光环宽度不变
C.液体对两种色光的折射率不同,较大者与较小者之比为
D.若光环b为单色光,这种光在液体中的传播速度比另一种色光的传播速度小
13.如图所示,水平桌面上有一折射率透明的玻璃半球,在球内有一离球心距离为的点光源S可向各个方向发光,点光源发出的所有光中刚好有一束光被反射回水平桌面。已知光在真空中的传播速度为,则由点光源S到反射回桌面的时间为( )
A.该束光在球形表面恰好发生全反射时的临界角为
B.该束光在球形表面恰好发生全反射时的临界角为
C.该束光由点光源S到反射回桌面的时间约为
D.该束光由点光源S到反射回桌面的时间约为
14.如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射入E点,并偏折到F点,已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则下列说法正确的是( )
A.该棱镜的折射率为 B.光在F点发生全反射
C.光从空气进入棱镜,波长变短 D.光从空气进入棱镜,波速变小
15.一透明介质的横截面为直角三角形,如图所示,一细束单色光从边上的点射入介质,经折射后的光线照到边的中点时恰好发生全反射。若,,,光在真空中传播的速度大小为,则( )
A.介质对该单色光的折射率为
B.介质对该单色光的折射率为
C.该单色光从点开始到第一次离开介质时所用的时间为
D.该单色光从点开始到第一次离开介质时所用的时间为
16.如图,ABC是横截面为直角三角形的玻璃三棱镜,一平行于CB边的细激光束从AC边上的某点射入棱镜后,在边上的D点部分反射、部分折射,其中反射光刚好与AC边平行。已知,,,空气中的光速为c。
①试通过计算,判断光束第一次射到BC边时是否发生全反射;
②求光束自进入棱镜到第一次从AC边射出所经历的时间。
17.如图所示,一种光学传感器是通过接收器Q接收到光的强度变化而触发工作的,光从挡风玻璃内侧Р点射向外侧M点再折射到空气中,测得入射角为,折射角为;光从Р点射向外侧N点,刚好发生全反射并被Q接收,已知挡风玻璃的厚度为d,光在空气中的传播速度为c,求:
①该挡风玻璃的折射率;
②光从P点射向外侧N点并被Q接收所需的时间。
18.如图,一个半径为R的圆形玻璃砖,为了测定该玻璃砖的折射率,将一条光线从玻璃砖上的A点射入,入射光线在过A点的横截面所在的平面内,玻璃砖横截面的圆心为O,在该横截面所在的平面内调节入射光线的方向,当圆形玻璃砖侧面上只有三处有光线射出时,测得入射光线与半径OA的夹角为,已知光在真空中传播的速度为。求:
(ⅰ)该玻璃砖的折射率;
(ⅱ)保持入射角不变,光线从射入玻璃砖到射出玻璃砖经历的最短时间。
19.如图所示,一个圆柱形油桶的底面直径为0.3m。当桶内没有油时,从A点经桶壁上边缘O点恰能看到桶壁上的B点。当桶内装满油时,仍沿方向看去,恰好看到桶壁上的C点。已知B点的深度为0.4m,间距为0.75m,真空中的光速。求:
(1)油的折射率;
(2)光在油中传播的速度。
20.某种透明材料制成的“n”形光学元件截面,内部半圆柱槽的半径为R,其他尺寸如图所示。一束激光(纸面内)从P点由空气中射入光学元件,入射角度,光束经折射后恰好与内圆柱面相切于Q点。已知P点在直径的延长线上,真空中的光速为c。
(1)求此材料对该激光的折射率n和该激光从P到Q经历的时间t;
(2)若仅改变人射光的人射角,使折射光线恰好在内圆柱面上发生全反射,求对应的入射角。
参考答案
1.B
【详解】
A.如图所示
根据几何关系
,
折射率
绿光在采光球中的传播速度为
故A错误;
B.红光折射率小,折射角大,则红光一定能从N点上方射出,故B正确;
C.紫光不可能直接折射经过O点,如果过的话,折射角为0°,故C错误;
D.光由光密到光疏可能发生全反射,则涂层折射率应大于管壁折射率,故D错误。
故选B。
2.D
【详解】
AB.光线在任一平行玻璃砖上面的折射角与下表面的入射角相等,根据光路可逆性,无论怎么增大或减小i都不会在玻璃砖下表面发生全反射,故A、B错误;
CD.在平行玻璃砖发生的侧移与玻璃砖的厚度成正比,随折射率的增大而增大,所以在一定时,,,故D正确,C错误。
故选D。
3.C
【详解】
如图当为全反射临界角时,光不会射出水面,即大于临界角时水面无可见光。因此等于临界角时射出的光为可见的最外部,临界角公式
根据折射定律
又
故
解得
所以最大半径为
故C正确。
故选C。
4.D
【详解】
A.如图,在A处
在P处的入射角
入射光与出射光相互垂直,m、L两法线垂直,
, ,
故A错误;
B.根据
故B错误;
C.临界角
故C错误;
D.如图 ,所以
故D正确。
故选D。
5.C
【详解】
A.甲中若减小入射角,根据折射定律和反射定律可知反射角和折射角都变小,则反射光线和折射光线之间的夹角将变大,故A错误;
B.减小入射角到0°时,不会发生折射现象,但是会有反射现象,所以光线不会全部从AB界面投射出去,故B错误;
CD.题图乙可知,当时发生全反射,则有
故C正确,D错误。
故选C。
6.C
【详解】
A.光的频率不变,波长与波速成正比,光从空气中射入玻璃中波速减小,则知光在玻璃中的波长比在空气中的波长小,故A错误;
BCD.作出如图所示光路图,设光线在棱镜中发生全反射的临界角为C,有
解得
C=45°
根据折射定律
解得
r=30°
由几何知识求得光线在CD面上的入射角θ=75°>45°,所以三条光线在CD面上都能发生全反射,且三条光线平行;由光路图可判断知距离C点最近的为光线1,故BD错误,C正确;
故选C。
7.D
【详解】
根据
得全反射临界角满足
光线射到三棱镜底边上的入射角为,因
其大于,所以光线在三棱镜底边上发生了全反射,没有折射光线,ABC错误,D正确。
故选D。
8.B
【详解】
A.由题分析可知,玻璃砖对b束光的折射率大于对a束光的折射率,则b光的频率高,故A错误;
B.由可知,由于玻璃砖对b束光的折射率大于对a束光的折射率,则a光比b光在玻璃砖中传播速度大,故B正确;
C.玻璃砖对b束光的折射率大于对a束光的折射率,则b光的频率高,由c=λf得知,在真空中,a光的波长大于b光的波长,故C错误;
D.由可知,a光的折射率小,则a光发生全反射的临界角大于b光,故D错误。
故选B。
9.C
【详解】
A.反射光线过圆心,射出时与圆形玻璃砖面垂直,不会发生色散现象,A错误;
B.根据光在玻璃中的传播的速度,红光频率最小,折射率最小,红光在玻璃砖中传播速度最大,B错误;
C.玻璃砖绕O点逆时针缓慢地转过角度θ的过程中,相当于玻璃砖不动,入射光线顺时针转动,折射光线随入射光线顺时针转动,折射光斑沿顺时针方向移动,C正确;
D.由临界角公式可知,紫光折射率最大,临界角最小,玻璃砖旋转过程中弧形屏上最先消失的一定是紫光,D错误。
故选C。
10.A
【详解】
根据折射率公式得
,
单色光在玻璃砖中通过的光程为
则单色光在玻璃砖中通过的时间为
故选A。
11.D
【详解】
A.由P点射入的光线在圆弧面上恰好发生全反射,由几何关系知
又因为
故
A错误;
B.由P点射入的光线进入玻璃砖后频率不变,B错误;
C.由几何关系可知,由Q点射入的光线在玻璃砖内运动的距离为
时间为
C错误;
D.设由Q点射入的光线在圆弧面上发生折射时的入射角和折射角分别为和,由折射定律知
设折射光线与水平轴OA的夹角为,由正弦定理得
由几何关系得
联立解得
D正确。
故选D。
12.AC
【详解】
A.液面形成光斑的原因是光在液体内部射向液面时发生了全反射,最边缘光线对应的入射角等于临界角,折射率小的光对应的临界角大,形成的光斑直径大;折射率大的光对应的临界角小,形成的光斑直径小,因为小光斑部分还有折射率小的色光,所以小光斑a是两种色光组成,光环b是单色光,A正确;
B.设光斑半径为r,边缘光线的光路如图所示
最大入射角为C等于全反射临界角,若h变大,C不变,则r变大,所以光斑面积变大,光环也变大,B错误;
C.根据几何关系可得折射率
由题知两个光亮的半径分别为15cm和21cm,液体深度为20cm,代入上式可求液体对两种色光的折射率之比为35:29,C正确;
D.由题知,b种色光在液面形成的光斑直径较大,对应的临界角较大,所以该种色光在液体中的折射率小,根据
可知该种色光在液体中传播的速度大, D错误。
故选AC。
13.AC
【详解】
AB.根据全反射的条件
解得
B错误A正确;
CD.光路如图,光源S发出的一条光线射到球面上的P点有
可得
即
对于位置已固定的光源,d与R都是定值,当 越大时,光线射出玻璃球的入射角α就越大,光线越容易发生全反射,点光源发出的所有光中刚好有一束发生全反射,即是当最大(θ=90°)时发生的全反射,如图所示
根据几何关系
根据
该束光由点光源S到反射回桌面的时间
解得
故选AC。
14.ACD
【详解】
A.在E点做出法线可知入射角为60°,折射角为30°,由
A正确;
B.由光路的可逆性可知,在BC边上的入射角小于临界角,不会发生全反射,B错误;
CD.由公式
可知,光从空气进入棱镜,波速变小,根据
光从空气进入棱镜,频率不变,波长变短,CD正确。
故选ACD。
15.AD
【详解】
AB.作出光路如图所示:
根据折射定律有
设光线到达BC边时发生全反射的临界角为,有
联立解得DE的长度为
介质对该单色光的折射率为
选项A正确,B错误;
CD.由可得
因为D为AC边的中点,E为边的中点,则DE∥AB,由几何关系可知,该光线在介质中传播的路程为
该光线在介质中的传播速度大小为
解得单色光从点开始到第一次离开介质时所用的时间
选项C错误,D正确。
故选AD。
16.①会发生全反射;②
【详解】
①设光在AC边的入射点为E,在BC边的反射点为F,在AC边的出射点为G,光路图图下图所示
由图结合题意可知,在D点的反射角为
为等边三角形,在E点折射时,入射角
折射角
根据折射定律
得
设发生全反射的临界角为C,则有
在F点,入射角为,因
故该处会发生全反射;
②光射至G点发生折射进入空气,由几何关系得
故光在棱镜中通过的路程
光在棱镜中的速度
由
联立解得
17.①;②
【详解】
①光线在M点发生折射,由于光线从光密介质射入光疏介质折射,则由折射定律得
②光在N点恰好发生全反射。则
即
光在介质中的传播速度为
光从点射向外侧点并被接收所需的时间
18.(ⅰ) ;(ⅱ)
【详解】
(ⅰ)根据对称性可知光在圆形玻璃砖内不会发生全反射,当圆形玻璃砖侧面上只有三处有光线射出时,三个光线出射点与圆心连线互成,作了光路图如图所示,三个出射点分别为B、C、A,则三角形ABC为等边三角形连接OA,即为折射角,根据几何关系可得
根据折射定律有
解得折射率
(ⅱ)通过分析可知光线第一次从B点射出时经历的时间最短,根据几何关系可得
光在玻璃砖里传播的速度为
则最短时间为
代入数据解得
19.(1)1.5;(2)
【详解】
(1)光路图如图所示
由几何关系可知:入射角与等大,折射角与等大
则
(2)由可得光在油中传播的速度为
20.(1),;(2)
【详解】
(1)光束经折射后恰好与内圆柱面相切于Q点,由题意可知,折射角为
根据
由几何关系可得
根据
从P到Q经历的时间
(2)如图所示
光束以入射角 由P点进入光学元件内折射到内圆面的C点,如果在C点发生全反射,则光束在球面上的入射角∠PCB等于临界角C
由正弦定理有
即
解得
根据
解得
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
