2020-2021学年人教版八年级数学上册12.2 三角形全等的判定(1)(共24张PPT)
文档属性
| 名称 | 2020-2021学年人教版八年级数学上册12.2 三角形全等的判定(1)(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
三角形全等的判定(1)
一、创设情境
某工厂生产一批三角形钢架,质检员张师傅和李师傅为了确保钢架的三边、三角均符合设计要求,每天要对产品作抽样检验。张师傅的检验方法是:用量角器和皮尺分别量出钢架的三条边和三个角,如果这六个数据合乎要求,他就认为产品合格。你认为张师傅的做法有道理吗?李师傅的检验方法是:用量角器量出钢架的一角,如果这个数据合乎要求,他就认为产品合格。你认为李师傅的做法有道理吗?为什么?一天,张师傅和李师傅因公外出,由周师傅来代班,可周师傅仅找到了皮尺,他可不可以进行工作呢?
我只需量一个角
我量三条边和三个角与样本核对
A
B
C
A′
B′
C′
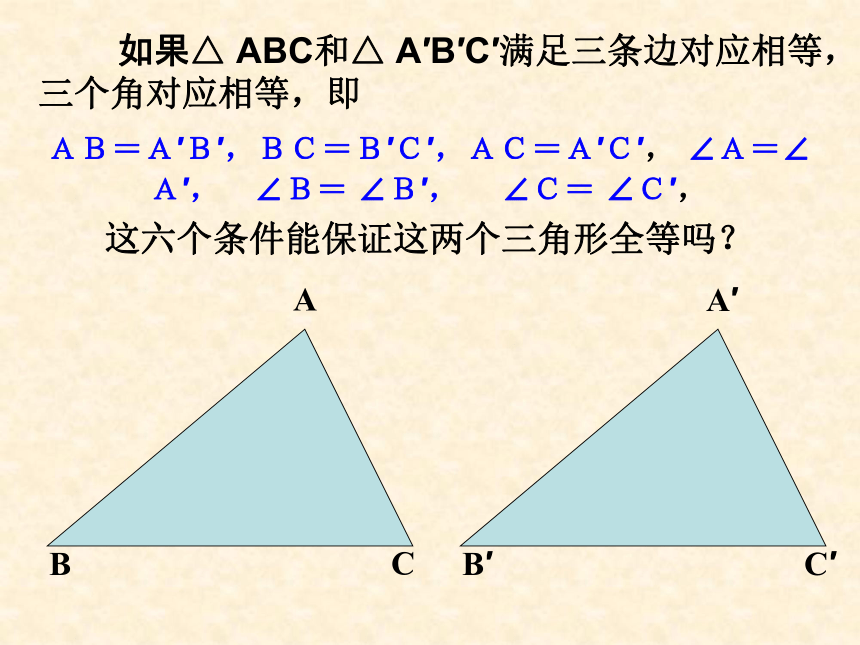
如果△
ABC和△
A′B′C′满足三条边对应相等,三个角对应相等,即
AB=A′B′,BC=B′C′,AC=A′C′,
∠A=∠A′, ∠B=
∠B′,
∠C=
∠C′,
这六个条件能保证这两个三角形全等吗?
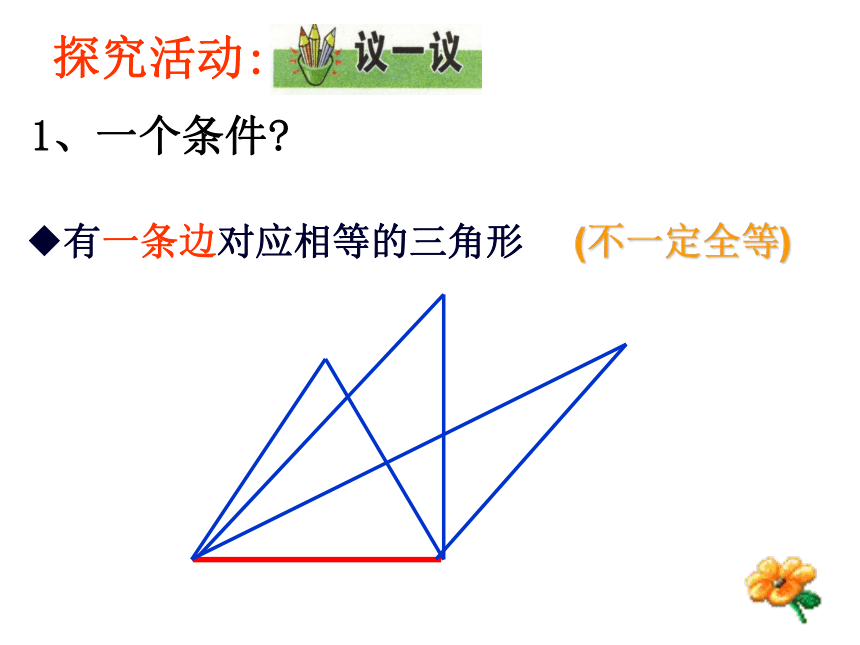
1、一个条件?
有一条边对应相等的三角形
(不一定全等)
探究活动:
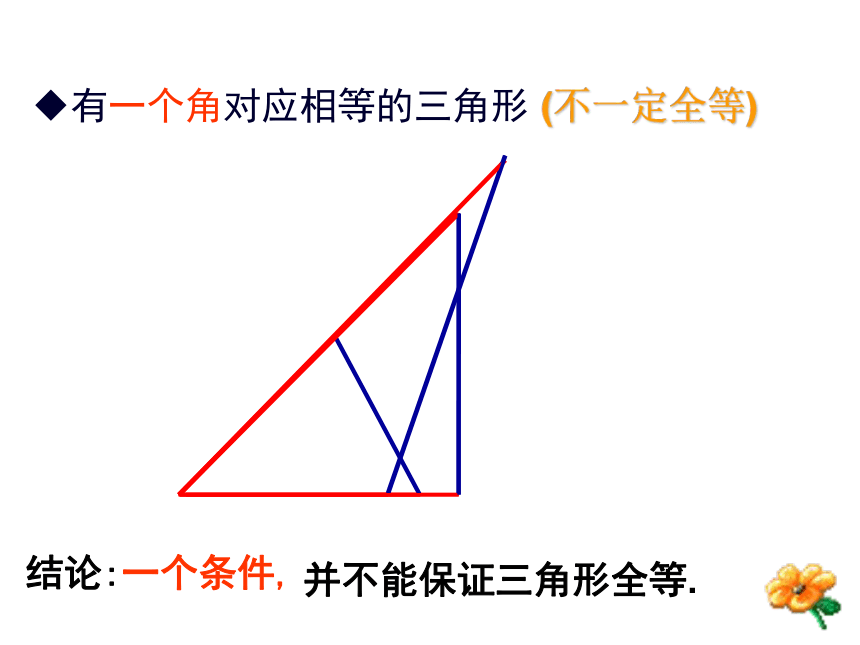
有一个角对应相等的三角形
结论:一个条件,
并不能保证三角形全等.
(不一定全等)
分别按照下面的条件做一做:
(1)三角形的两条边分别为2cm、4cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的一个内角为30°,一条边为3cm.
2、两个条件?
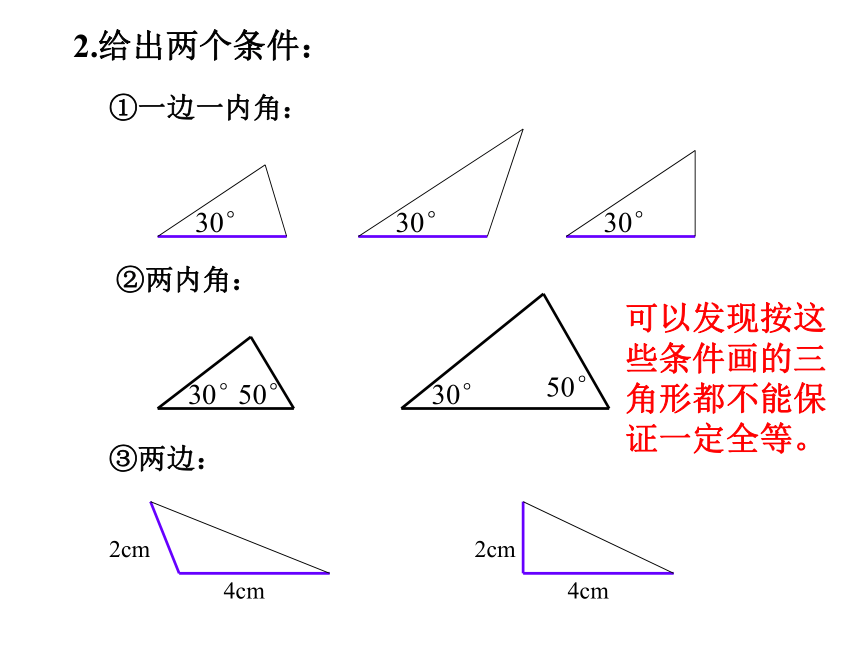
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不能保证一定全等。
想一想:先任意画一个△ABC,怎样再画△A'B'C'
,使
A'B'=AB
,B'C'=BC,A'C'=
AC
做一做:画△A′B′C′,再把画好的△A'B'C'剪下放到△ABC上,看他们重合吗?
说一说:你发现了什么?
活动二
判断两个三角形全等的推理过程,叫做证明三角形全等。
A
B
C
D
E
F
用
数学语言表述:
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
C
A
B
D
O
下图中,要证两个三角形全等,还需要哪些条件,补充填空:
在△AOB和△DOC中
AO=DO(已知)
______=______(已知)
AB=DC(已知)
∴
△AOB≌△DOC(
)
SSS
BO
CO
AB
=
DC(已知)
AC
=
DB(已知)
△ABC≌
△DCB
A
B
C
D
BC
CB
(SSS)
注意公共边这个隐含条件
=
(公共边)
在△ABC
和△DCB中
应用迁移,巩固提高
例1.
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD
分析:要证明△
ABD≌
△
ACD,首先看这两个三角形的三条边是否对应相等。
结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。
归纳:
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
A
B
C
D
A
B
C
D
变变看
若AB=AC,BD=CD,那么△
ABD和△
ACD全等吗?
取三根长度适当的木条,用钉子钉成一个三角形的框架,你所得到的框架的形状固定吗?用四根木条钉成的框架的形状固定吗?
活动三
思考:你能用“边边边”解释三角形具有稳定性吗?
用三根木条钉成的三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。三角形的稳定性在生产和生活中是很有用的。如:房屋的人字梁具有三角形的结构,它就坚固和稳定。
大家想一想,如何才能使用四根木条钉成的形状的框架不能活动?
活动三
小结
2.
三边对应相等的两个三角形全等(边边边或SSS);
3.书写格式:①准备条件;
②三角形全等书写的三步骤。
1.知道三角形三条边的长度怎样画三角形。
作业布置:
必做:
课本P7
例1结论改为
求证:(1)AD平分
∠BAC.
(2)AD⊥BC.
(3)你发现了什么?
选做:探究满足
“两角一边”或“两边一角”或“三 个角”的条件能否判断两个三角形全等?
数学的伟大使命,
在于从混沌中发现有序
三角形全等的判定(1)
一、创设情境
某工厂生产一批三角形钢架,质检员张师傅和李师傅为了确保钢架的三边、三角均符合设计要求,每天要对产品作抽样检验。张师傅的检验方法是:用量角器和皮尺分别量出钢架的三条边和三个角,如果这六个数据合乎要求,他就认为产品合格。你认为张师傅的做法有道理吗?李师傅的检验方法是:用量角器量出钢架的一角,如果这个数据合乎要求,他就认为产品合格。你认为李师傅的做法有道理吗?为什么?一天,张师傅和李师傅因公外出,由周师傅来代班,可周师傅仅找到了皮尺,他可不可以进行工作呢?
我只需量一个角
我量三条边和三个角与样本核对
A
B
C
A′
B′
C′
如果△
ABC和△
A′B′C′满足三条边对应相等,三个角对应相等,即
AB=A′B′,BC=B′C′,AC=A′C′,
∠A=∠A′, ∠B=
∠B′,
∠C=
∠C′,
这六个条件能保证这两个三角形全等吗?
1、一个条件?
有一条边对应相等的三角形
(不一定全等)
探究活动:
有一个角对应相等的三角形
结论:一个条件,
并不能保证三角形全等.
(不一定全等)
分别按照下面的条件做一做:
(1)三角形的两条边分别为2cm、4cm.
(2)三角形的两个内角分别为30°和50°.
(3)三角形的一个内角为30°,一条边为3cm.
2、两个条件?
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不能保证一定全等。
想一想:先任意画一个△ABC,怎样再画△A'B'C'
,使
A'B'=AB
,B'C'=BC,A'C'=
AC
做一做:画△A′B′C′,再把画好的△A'B'C'剪下放到△ABC上,看他们重合吗?
说一说:你发现了什么?
活动二
判断两个三角形全等的推理过程,叫做证明三角形全等。
A
B
C
D
E
F
用
数学语言表述:
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
C
A
B
D
O
下图中,要证两个三角形全等,还需要哪些条件,补充填空:
在△AOB和△DOC中
AO=DO(已知)
______=______(已知)
AB=DC(已知)
∴
△AOB≌△DOC(
)
SSS
BO
CO
AB
=
DC(已知)
AC
=
DB(已知)
△ABC≌
△DCB
A
B
C
D
BC
CB
(SSS)
注意公共边这个隐含条件
=
(公共边)
在△ABC
和△DCB中
应用迁移,巩固提高
例1.
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD
分析:要证明△
ABD≌
△
ACD,首先看这两个三角形的三条边是否对应相等。
结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。
归纳:
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
A
B
C
D
A
B
C
D
变变看
若AB=AC,BD=CD,那么△
ABD和△
ACD全等吗?
取三根长度适当的木条,用钉子钉成一个三角形的框架,你所得到的框架的形状固定吗?用四根木条钉成的框架的形状固定吗?
活动三
思考:你能用“边边边”解释三角形具有稳定性吗?
用三根木条钉成的三角形框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。三角形的稳定性在生产和生活中是很有用的。如:房屋的人字梁具有三角形的结构,它就坚固和稳定。
大家想一想,如何才能使用四根木条钉成的形状的框架不能活动?
活动三
小结
2.
三边对应相等的两个三角形全等(边边边或SSS);
3.书写格式:①准备条件;
②三角形全等书写的三步骤。
1.知道三角形三条边的长度怎样画三角形。
作业布置:
必做:
课本P7
例1结论改为
求证:(1)AD平分
∠BAC.
(2)AD⊥BC.
(3)你发现了什么?
选做:探究满足
“两角一边”或“两边一角”或“三 个角”的条件能否判断两个三角形全等?
数学的伟大使命,
在于从混沌中发现有序
