2021-2022学年沪科版 九年级数学上册 第二十一章 二次函数 复习课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年沪科版 九年级数学上册 第二十一章 二次函数 复习课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
二次函数复习课
二次函数的定义:
形如y=ax2+bx+c
(a,b,c是常数,a≠0)
的函数叫做二次函数
想一想:函数的自变量x是否可以取任何值呢?
注意:当二次函数表示某个实际问题时,还必须根据题意确定自变量的取值范围.
二次函数的一般形式
函数y=ax2+bx+c
其中a、b、c是常数
切记:a≠0
右边一个x的二次多项式(不能是分式或根式)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
知识运用
下列函数中,哪些是二次函数?
(1)y=3x-1
(2)y=3x2
(3)y=3x3+2x2
(4)y=2x2-2x+1
(5)y=x
-2
+x
(6)y=x2-x(1+x)
驶向胜利的彼岸
当m取何值时,函数是y=
(m+2)x
分别
是一次函数?
反比例函数?
知识运用
m2-2
二次函数?
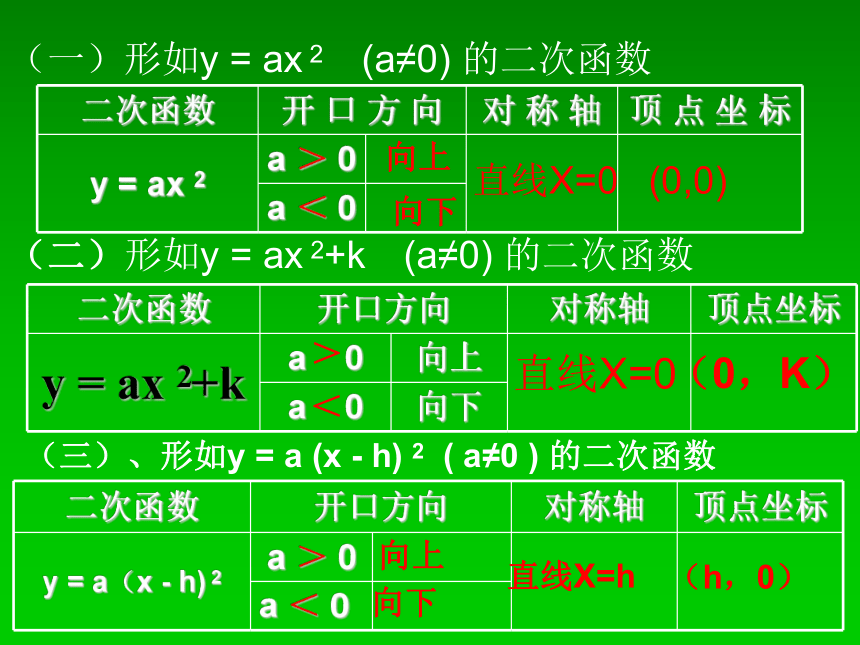
(一)形如y
=
ax
2 (a≠0)
的二次函数
二次函数
开
口
方
向
对
称
轴
顶
点
坐
标
y
=
ax
2
a
>
0
a
<
0
向上
向下
直线X=0
(0,0)
(二)形如y
=
ax
2+k (a≠0)
的二次函数
二次函数
开口方向
对称轴
顶点坐标
y
=
ax
2+k
a
0
向上
a
0
向下
>
<
直线X=0
(0,K)
二次函数
开口方向
对称轴
顶点坐标
y
=
a(x
-
h)
2
a
>
0
a
<
0
向上
向下
直线X=h
(h,0)
(三)、形如y
=
a
(x
-
h)
2
(
a≠0
)
的二次函数
巩固练习1:
(1)抛物线y
=
x
2的开口向
,对称轴是
,顶点坐标是
,图象过第
象限
;
(2)已知y
=
-
nx
2
(n>0)
,
则图象
(
)
(填“可能”或“不可能”)过点A(-2,3)。
上
Y轴
(0,0)
一、二
不可能
(3)抛物线y
=
x
2+3的开口向
,对称轴是
,
顶点坐标是
,是由抛物线
y
=
x
2向
平移
个单位得到的;
上
直线X=0
(0,3)
上
3
(2)已知(如图)抛物线y
=
ax
2+k的图象,则a
0,k
0;若图象过A
(0,-2)
和B
(2,0)
,则a
=
,k
=
;函数关系式是y
=
。
〉
〈
0.5
-2
0.5x
2-2
X
Y
A
B
O
(四)
形如y
=
a
(x+h)
2
+k
(a
≠0)
的二次函数
二次函数
开口方向
对称轴
顶点坐标
y
=
a(x+h)
2+k
向上
向下
a
>
0
a
<
0
直线X=-h
(-h,k)
练习巩固2:
(1)抛物线
y
=
2
(x
–3
)
2+1
的开口向
,
对称轴
,
顶点坐标是
(2)若抛物线y
=
a
(x+m)
2+n开口向下,顶点在第四象限,则a
0,
m
0,
n
0。
上
X=3
(3,1)
〈
〈
〈
2、已知二次函数y=-
x2+bx-5的图象的顶点在y轴上,则b=___。
1
2
0
-1
-2
-3
-4
0
1
2
3
4
?
?
?
?
?
?
?
?
1
2
3
4
5
6
-1
-2
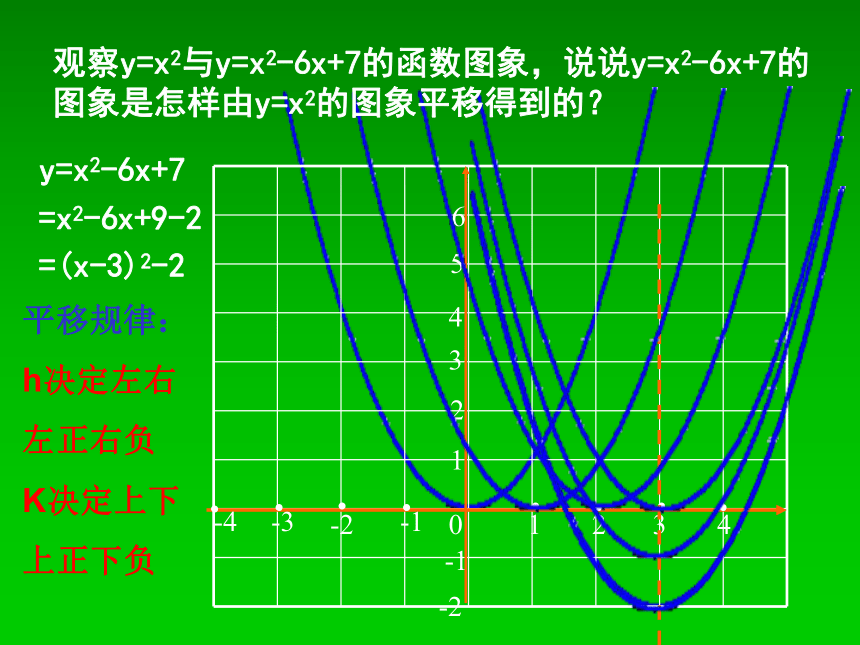
观察y=x2与y=x2-6x+7的函数图象,说说y=x2-6x+7的图象是怎样由y=x2的图象平移得到的?
y=x2-6x+7
=x2-6x+9-2
=(x-3)2-2
平移规律:
h决定左右
左正右负
K决定上下
上正下负
基础练习
1.由y=2x2的图象向左平移两个单位,再向下平
移三个单位,得到的图象的函数解析式为
________________________
2.由函数y=
-3(x-1)2+2的图象向右平移4个单位,
再向上平移3个单位,得到的图象的函数解析式
为_____________________________
y=2(x+2)2-3
=2x2+8x+5
y=
-
3(x-1-4)2+2+3
=-3x2+30x-70
3.抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;
y=2(x+1)2-8
4.将抛物线y=x2-6x+4如何移动才能得到y=x2.
逆向思考,由y=x2-6x+4
=(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.
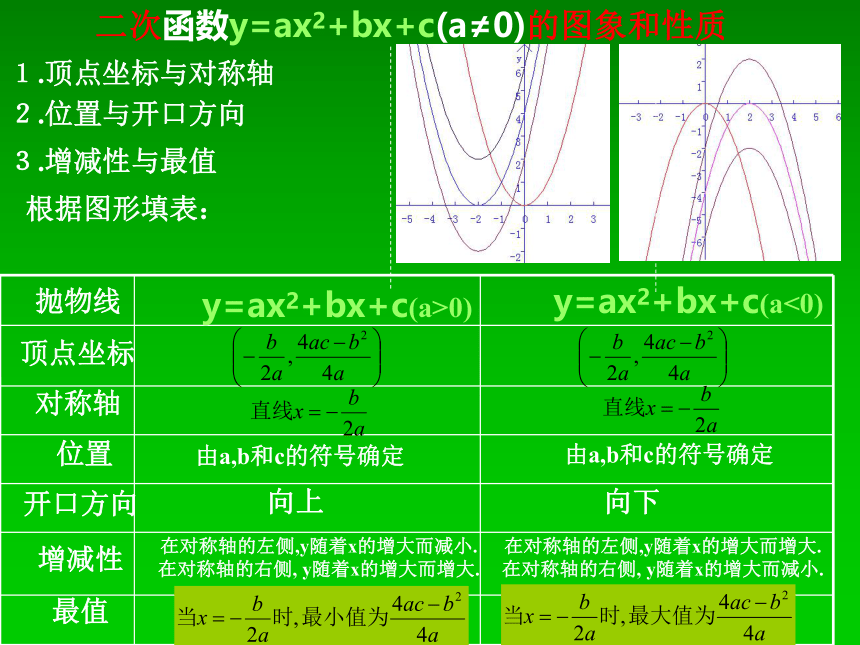
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
根据图形填表:
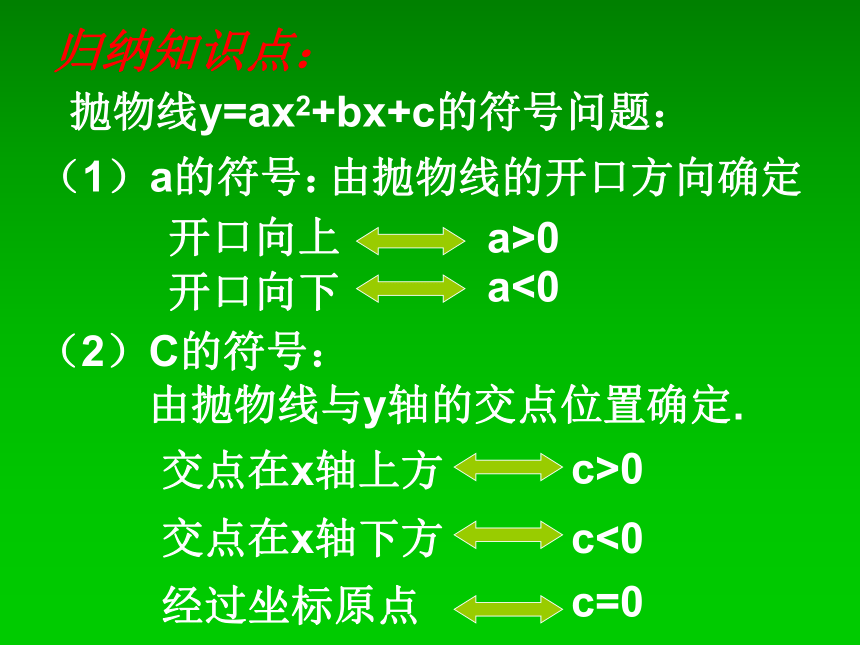
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
(3)b的符号:
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
17.根据下列表格中二次函数y=ax2+bx+c的自变量与函数值的对应值,判断方程ax2+bx+c
=0
(a≠0,
a,
b,
c为常数)的一个解的范围是(
)
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
-0.03
-0.01
0.02
0.04
A.6.17<
X
<6.18
B.6.18<
X
<6.19
C.-0.01<
X
<0.02
D.6.19<
X
<6.20
B
3、已知二次函数
的图象如图所示,则函数
的图象只可能是(
)
y
x
0
2
-3
(16)小明从右边的二次函数y=ax2+bx+c的图象观察得出下面的五条信息:①
a<
0;②
c=0;③
函数的最小值为-3;
④当x<0时,y>0;
⑤当0<x1<x2<2时,y1
>
y2
你认为其中正确的个数有(
)
A.2
B.3
C.4
D.5
C
练一练:已知y=ax2+bx+c的图象如图所示,
a___0,
b____0,
c_____0,
abc____0
b___2a,
2a-b_____0,
2a+b_______0
b2-4ac_____0
a+b+c_____0,
a-b+c____0
4a-2b+c_____0
0
-1
1
-2
<
<
<
<
>
>
>
<
>
>
>
二次函数与一元二次方程
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac
>
0
有一个交点
有两个相等的实数根
b2-4ac
=
0
没有交点
没有实数根
b2-4ac
<
0
选择
抛物线y=x2-4x+3的对称轴是_____________.
A
直线x=1
B直线x=
-1
C
直线x=2
D直线x=
-2
(2)抛物线y=3x2-1的________________
A
开口向上,有最高点
B
开口向上,有最低点
C
开口向下,有最高点
D
开口向下,有最低点
(3)若y=ax2+bx+c(a
?
0)与轴交于点A(2,0),
B(4,0),
则对称轴是_______
A
直线x=2
B直线x=4
C
直线x=3
D直线x=
-3
(4)若y=ax2+bx+c(a
?
0)与轴交于点A(2,m),
B(4,m),
则对称轴是_______
A
直线x=3
B
直线x=4
C
直线x=
-3
D直线x=2
c
B
C
A
2、已知抛物线顶点坐标(h,
k),通常设抛物线解析式为_______________
3、已知抛物线与x
轴的两个交点(x1,0)、
(x2,0),通常设解析式为_____________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2)
(a≠0)
求抛物线解析式的三种方法
练习 根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0),
(1,-2)
,
(2,3)
三点;
(2)、图象的顶点(2,3),
且经过点(3,1)
;
(3)、图象经过(-2,0),
(3,0)
,且最高点
的纵坐标是3
。
例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为(
1
,
2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a
(3-1)2+2
∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即:
y=-2x2+4x
综合创新:
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.
解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同?
a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
?
顶点为(1,5)或(1,-5)
所以其解析式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
2.若a+b+c=0,a?0,把抛物线y=ax2+bx+c向下
平移4个单位,再向左平移5个单位所到的新
抛物线的顶点是(-2,0),求原抛物线的解析式.
分析:
(1)由a+b+c=0可知,原抛物线的图象经过(1,0)
(2)
新抛物线向右平移5个单位,
再向上平移4个单位即得原抛物线
答案:y=-x2+6x-5
练习1、已知抛物线y=ax2+bx-1的对称轴是x=1
,
最高点在直线y=2x+4上。
(1)
求此抛物线的顶点坐标.
(2)求抛物线解析式.
(3)求抛物线与直线的交点坐标.
解:∵二次函数的对称轴是x=1
∴图象的顶点横坐标为1
又∵图象的最高点在直线y=2x+4上
∴当x=1时,y=6
∴顶点坐标为(
1
,
6)
例2、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。
解:
∵点A在正半轴,点B在负半轴
OA=4,∴点A(4,0)
OB=1,
∴点B(-1,0)
∵
∠ACB=90°OC⊥
AB
∴
∠
CAO=∠BCO
∠CAO+∠OCA=90,∠OCA+∠BCO=90
∴∠BOC=∠COA,
∴△BOC∽△COA
∴OB/OC=OC/OA
∴OC=2,点C(0,-2)
由题意可设y=a(x+1)(x-4)得:
a(0+1)(0-4)=-2
∴a=0.5
∴
y=0.5(x+1)(x-4)
A
B
x
y
O
C
练习、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。
y
O
x
(3)、求它的解析式和顶点坐标;
2.5
0
x
y
h
A
B
D
河北省赵县的赵州桥的桥拱是抛物线型,建立如图所
示的坐标系,其函数的表达式为y=
-
x2
,
当水位线在AB位
置时,水面宽
AB
=
30米,这时水面离桥顶的高度h是(
)
A、5米
B、6米;
C、8米;
D、9米
1
25
解:当x=15时,
Y=-1/25
×
152
=-9
问题1:
问题4:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
分析:利润=(每件商品所获利润)×
(销售件数)
设每个涨价x元,
那么
(3)销售量可以表示为
(1)销售价可以表示为
(50+x)元(x≥
0,且为整数)
(500-10x)
个
(2)一个商品所获利润可以表示为
(50+x-40)元
(4)共获利润可以表示为
(50+x-40)(500-10x)元
答:定价为70元/个,利润最高为9000元.
解:
y=(50+x-40)(500-10x)
=-10
x2
+400x+5000
(0
≤
x≤50
,且为整数
)
=-
10(x-20)2
+9000
问题4:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
问题5:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
解:
(1)
∵
AB为x米、篱笆长为24米
∴
花圃另一边为(24-4x)米
(3)
∵墙的可用长度为8米
(2)当x=
时,S最大值=
=36(平方米)
∴
S=x(24-4x)
=-4x2+24
x
(0∴
0<24-4x
≤8
4≤x<6
∴当x=4m时,S最大值=32
平方米
小试牛刀
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?
A
B
C
P
Q
解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:
AP=2x
cm
PB=(8-2x
)
cm
QB=x
cm
则
y=1/2
x(8-2x)
=-x2
+4x
=-(x2
-4x
+4
-4)
=
-(x
-
2)2
+
4
所以,当P、Q同时运动2秒后ΔPBQ的面积y最大最大面积是
4cm2
(0A
B
C
P
Q
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P,Q分别从A,B同时出发,几秒后ΔPBQ的面积最大?最大面积是多少?
在矩形荒地ABCD中,AB=10,BC=6,今在四边上分别选取E、F、G、H四点,且AE=AH=CF=CG=x,建一个花园,如何设计,可使花园面积最大?
D
C
A
B
G
H
F
E
10
6
再显身手
解:设花园的面积为y
则
y=60-x2
-(10-x)(6-x)
=-2x2
+
16x
(0=-2(x-4)2
+
32
所以当x=4时
花园的最大面积为32
实际问题
抽象
转化
数学问题
运用
数学知识
问题的解
谈谈你的学习体会
“二次函数应用”
的思路
1.理解问题;
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.解题求解;
5.检验结果的合理性,拓展等.
二次函数复习课
二次函数的定义:
形如y=ax2+bx+c
(a,b,c是常数,a≠0)
的函数叫做二次函数
想一想:函数的自变量x是否可以取任何值呢?
注意:当二次函数表示某个实际问题时,还必须根据题意确定自变量的取值范围.
二次函数的一般形式
函数y=ax2+bx+c
其中a、b、c是常数
切记:a≠0
右边一个x的二次多项式(不能是分式或根式)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
知识运用
下列函数中,哪些是二次函数?
(1)y=3x-1
(2)y=3x2
(3)y=3x3+2x2
(4)y=2x2-2x+1
(5)y=x
-2
+x
(6)y=x2-x(1+x)
驶向胜利的彼岸
当m取何值时,函数是y=
(m+2)x
分别
是一次函数?
反比例函数?
知识运用
m2-2
二次函数?
(一)形如y
=
ax
2 (a≠0)
的二次函数
二次函数
开
口
方
向
对
称
轴
顶
点
坐
标
y
=
ax
2
a
>
0
a
<
0
向上
向下
直线X=0
(0,0)
(二)形如y
=
ax
2+k (a≠0)
的二次函数
二次函数
开口方向
对称轴
顶点坐标
y
=
ax
2+k
a
0
向上
a
0
向下
>
<
直线X=0
(0,K)
二次函数
开口方向
对称轴
顶点坐标
y
=
a(x
-
h)
2
a
>
0
a
<
0
向上
向下
直线X=h
(h,0)
(三)、形如y
=
a
(x
-
h)
2
(
a≠0
)
的二次函数
巩固练习1:
(1)抛物线y
=
x
2的开口向
,对称轴是
,顶点坐标是
,图象过第
象限
;
(2)已知y
=
-
nx
2
(n>0)
,
则图象
(
)
(填“可能”或“不可能”)过点A(-2,3)。
上
Y轴
(0,0)
一、二
不可能
(3)抛物线y
=
x
2+3的开口向
,对称轴是
,
顶点坐标是
,是由抛物线
y
=
x
2向
平移
个单位得到的;
上
直线X=0
(0,3)
上
3
(2)已知(如图)抛物线y
=
ax
2+k的图象,则a
0,k
0;若图象过A
(0,-2)
和B
(2,0)
,则a
=
,k
=
;函数关系式是y
=
。
〉
〈
0.5
-2
0.5x
2-2
X
Y
A
B
O
(四)
形如y
=
a
(x+h)
2
+k
(a
≠0)
的二次函数
二次函数
开口方向
对称轴
顶点坐标
y
=
a(x+h)
2+k
向上
向下
a
>
0
a
<
0
直线X=-h
(-h,k)
练习巩固2:
(1)抛物线
y
=
2
(x
–3
)
2+1
的开口向
,
对称轴
,
顶点坐标是
(2)若抛物线y
=
a
(x+m)
2+n开口向下,顶点在第四象限,则a
0,
m
0,
n
0。
上
X=3
(3,1)
〈
〈
〈
2、已知二次函数y=-
x2+bx-5的图象的顶点在y轴上,则b=___。
1
2
0
-1
-2
-3
-4
0
1
2
3
4
?
?
?
?
?
?
?
?
1
2
3
4
5
6
-1
-2
观察y=x2与y=x2-6x+7的函数图象,说说y=x2-6x+7的图象是怎样由y=x2的图象平移得到的?
y=x2-6x+7
=x2-6x+9-2
=(x-3)2-2
平移规律:
h决定左右
左正右负
K决定上下
上正下负
基础练习
1.由y=2x2的图象向左平移两个单位,再向下平
移三个单位,得到的图象的函数解析式为
________________________
2.由函数y=
-3(x-1)2+2的图象向右平移4个单位,
再向上平移3个单位,得到的图象的函数解析式
为_____________________________
y=2(x+2)2-3
=2x2+8x+5
y=
-
3(x-1-4)2+2+3
=-3x2+30x-70
3.抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;
y=2(x+1)2-8
4.将抛物线y=x2-6x+4如何移动才能得到y=x2.
逆向思考,由y=x2-6x+4
=(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
根据图形填表:
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
(3)b的符号:
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
17.根据下列表格中二次函数y=ax2+bx+c的自变量与函数值的对应值,判断方程ax2+bx+c
=0
(a≠0,
a,
b,
c为常数)的一个解的范围是(
)
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
-0.03
-0.01
0.02
0.04
A.6.17<
X
<6.18
B.6.18<
X
<6.19
C.-0.01<
X
<0.02
D.6.19<
X
<6.20
B
3、已知二次函数
的图象如图所示,则函数
的图象只可能是(
)
y
x
0
2
-3
(16)小明从右边的二次函数y=ax2+bx+c的图象观察得出下面的五条信息:①
a<
0;②
c=0;③
函数的最小值为-3;
④当x<0时,y>0;
⑤当0<x1<x2<2时,y1
>
y2
你认为其中正确的个数有(
)
A.2
B.3
C.4
D.5
C
练一练:已知y=ax2+bx+c的图象如图所示,
a___0,
b____0,
c_____0,
abc____0
b___2a,
2a-b_____0,
2a+b_______0
b2-4ac_____0
a+b+c_____0,
a-b+c____0
4a-2b+c_____0
0
-1
1
-2
<
<
<
<
>
>
>
<
>
>
>
二次函数与一元二次方程
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点
一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac
>
0
有一个交点
有两个相等的实数根
b2-4ac
=
0
没有交点
没有实数根
b2-4ac
<
0
选择
抛物线y=x2-4x+3的对称轴是_____________.
A
直线x=1
B直线x=
-1
C
直线x=2
D直线x=
-2
(2)抛物线y=3x2-1的________________
A
开口向上,有最高点
B
开口向上,有最低点
C
开口向下,有最高点
D
开口向下,有最低点
(3)若y=ax2+bx+c(a
?
0)与轴交于点A(2,0),
B(4,0),
则对称轴是_______
A
直线x=2
B直线x=4
C
直线x=3
D直线x=
-3
(4)若y=ax2+bx+c(a
?
0)与轴交于点A(2,m),
B(4,m),
则对称轴是_______
A
直线x=3
B
直线x=4
C
直线x=
-3
D直线x=2
c
B
C
A
2、已知抛物线顶点坐标(h,
k),通常设抛物线解析式为_______________
3、已知抛物线与x
轴的两个交点(x1,0)、
(x2,0),通常设解析式为_____________
1、已知抛物线上的三点,通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x-h)2+k(a≠0)
y=a(x-x1)(x-x2)
(a≠0)
求抛物线解析式的三种方法
练习 根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0),
(1,-2)
,
(2,3)
三点;
(2)、图象的顶点(2,3),
且经过点(3,1)
;
(3)、图象经过(-2,0),
(3,0)
,且最高点
的纵坐标是3
。
例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。
解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为(
1
,
2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a
(3-1)2+2
∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即:
y=-2x2+4x
综合创新:
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.
解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同?
a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
?
顶点为(1,5)或(1,-5)
所以其解析式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
2.若a+b+c=0,a?0,把抛物线y=ax2+bx+c向下
平移4个单位,再向左平移5个单位所到的新
抛物线的顶点是(-2,0),求原抛物线的解析式.
分析:
(1)由a+b+c=0可知,原抛物线的图象经过(1,0)
(2)
新抛物线向右平移5个单位,
再向上平移4个单位即得原抛物线
答案:y=-x2+6x-5
练习1、已知抛物线y=ax2+bx-1的对称轴是x=1
,
最高点在直线y=2x+4上。
(1)
求此抛物线的顶点坐标.
(2)求抛物线解析式.
(3)求抛物线与直线的交点坐标.
解:∵二次函数的对称轴是x=1
∴图象的顶点横坐标为1
又∵图象的最高点在直线y=2x+4上
∴当x=1时,y=6
∴顶点坐标为(
1
,
6)
例2、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。
解:
∵点A在正半轴,点B在负半轴
OA=4,∴点A(4,0)
OB=1,
∴点B(-1,0)
∵
∠ACB=90°OC⊥
AB
∴
∠
CAO=∠BCO
∠CAO+∠OCA=90,∠OCA+∠BCO=90
∴∠BOC=∠COA,
∴△BOC∽△COA
∴OB/OC=OC/OA
∴OC=2,点C(0,-2)
由题意可设y=a(x+1)(x-4)得:
a(0+1)(0-4)=-2
∴a=0.5
∴
y=0.5(x+1)(x-4)
A
B
x
y
O
C
练习、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。
y
O
x
(3)、求它的解析式和顶点坐标;
2.5
0
x
y
h
A
B
D
河北省赵县的赵州桥的桥拱是抛物线型,建立如图所
示的坐标系,其函数的表达式为y=
-
x2
,
当水位线在AB位
置时,水面宽
AB
=
30米,这时水面离桥顶的高度h是(
)
A、5米
B、6米;
C、8米;
D、9米
1
25
解:当x=15时,
Y=-1/25
×
152
=-9
问题1:
问题4:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
分析:利润=(每件商品所获利润)×
(销售件数)
设每个涨价x元,
那么
(3)销售量可以表示为
(1)销售价可以表示为
(50+x)元(x≥
0,且为整数)
(500-10x)
个
(2)一个商品所获利润可以表示为
(50+x-40)元
(4)共获利润可以表示为
(50+x-40)(500-10x)元
答:定价为70元/个,利润最高为9000元.
解:
y=(50+x-40)(500-10x)
=-10
x2
+400x+5000
(0
≤
x≤50
,且为整数
)
=-
10(x-20)2
+9000
问题4:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
问题5:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
解:
(1)
∵
AB为x米、篱笆长为24米
∴
花圃另一边为(24-4x)米
(3)
∵墙的可用长度为8米
(2)当x=
时,S最大值=
=36(平方米)
∴
S=x(24-4x)
=-4x2+24
x
(0
0<24-4x
≤8
4≤x<6
∴当x=4m时,S最大值=32
平方米
小试牛刀
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?
A
B
C
P
Q
解:根据题意,设经过x秒后ΔPBQ的面积y最大,则:
AP=2x
cm
PB=(8-2x
)
cm
QB=x
cm
则
y=1/2
x(8-2x)
=-x2
+4x
=-(x2
-4x
+4
-4)
=
-(x
-
2)2
+
4
所以,当P、Q同时运动2秒后ΔPBQ的面积y最大最大面积是
4cm2
(0
B
C
P
Q
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,点P从点A开始沿AB边向点B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P,Q分别从A,B同时出发,几秒后ΔPBQ的面积最大?最大面积是多少?
在矩形荒地ABCD中,AB=10,BC=6,今在四边上分别选取E、F、G、H四点,且AE=AH=CF=CG=x,建一个花园,如何设计,可使花园面积最大?
D
C
A
B
G
H
F
E
10
6
再显身手
解:设花园的面积为y
则
y=60-x2
-(10-x)(6-x)
=-2x2
+
16x
(0
+
32
所以当x=4时
花园的最大面积为32
实际问题
抽象
转化
数学问题
运用
数学知识
问题的解
谈谈你的学习体会
“二次函数应用”
的思路
1.理解问题;
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.解题求解;
5.检验结果的合理性,拓展等.
