3.1.1.2基本计数原理的应用同步练习-2021-2022学年高二数学人教版B版(2019)选择性必修第二册(Word含答案解析)
文档属性
| 名称 | 3.1.1.2基本计数原理的应用同步练习-2021-2022学年高二数学人教版B版(2019)选择性必修第二册(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 108.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览


文档简介
基本计数原理的应用
一、选择题
1.将3张不同的奥运会门票分给10名同学中的3人,每人1张,则不同分法的种数是( )
A.2 160 B.720 C.240 D.120
2.用0,1,…,9这10个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252 C.261 D.648
3.某城市的电话号码由六位升为七位(首位数字均不为零),则该城市可增加的电话部数是( )
A.9×8×7×6×5×4×3×2
B.8×96
C.9×106
D.8.1×106
4.有A,B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车床,丙只会操作A种车床,要从这三名工人中选两名分别去操作这两种车床,则不同的选派方法有( )
A.6种 B.5种 C.4种 D.3种
5.有四位教师在同一年级的四个班各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则监考的方法有( )
A.8种 B.9种 C.10种 D.11种
二、填空题
6.从3名男生和4名女生中选出2人分别担任2项不同的社区活动服务者,要求男、女生各1人,那么不同的安排方法有________种(用数字作答).
7.有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有不同的取法______种.
8.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有________种.
三、解答题
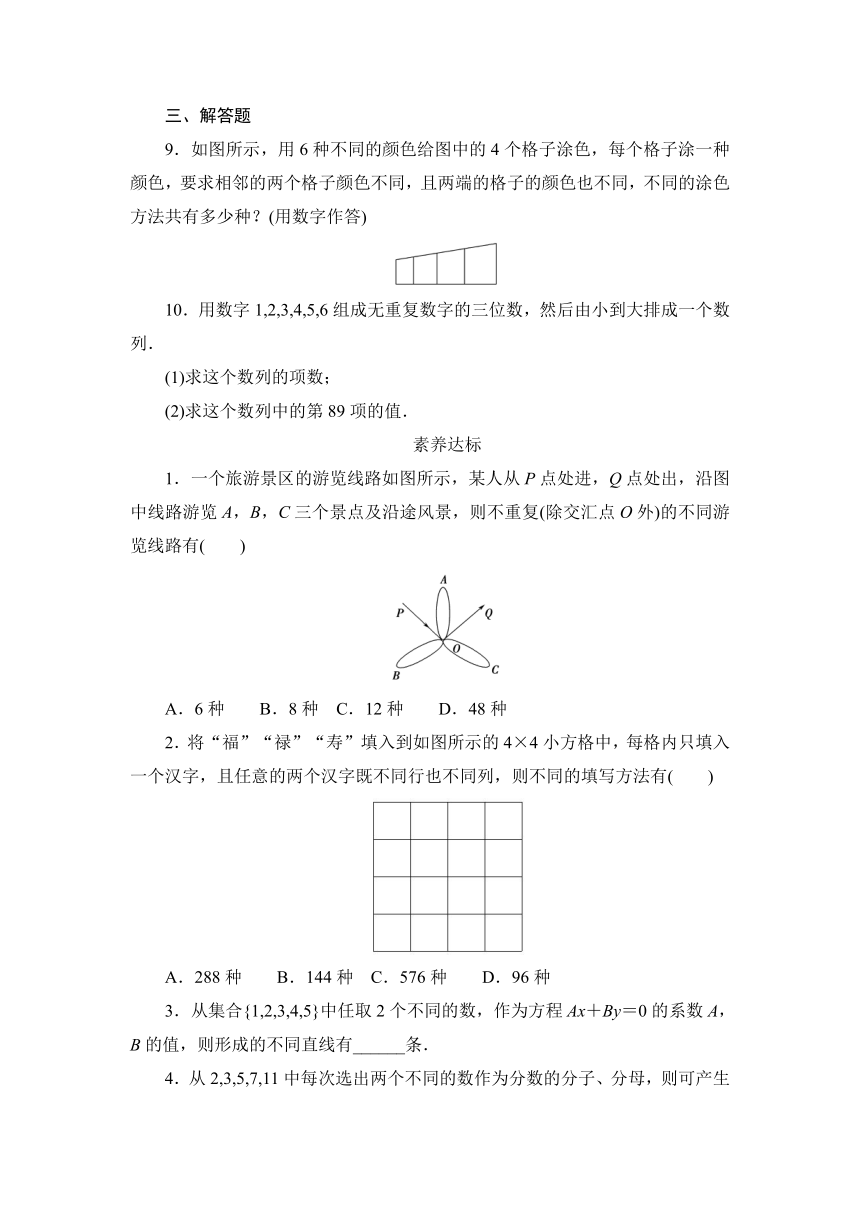
9.如图所示,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,不同的涂色方法共有多少种?(用数字作答)
10.用数字1,2,3,4,5,6组成无重复数字的三位数,然后由小到大排成一个数列.
(1)求这个数列的项数;
(2)求这个数列中的第89项的值.
素养达标
1.一个旅游景区的游览线路如图所示,某人从P点处进,Q点处出,沿图中线路游览A,B,C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )
A.6种 B.8种 C.12种 D.48种
2.将“福”“禄”“寿”填入到如图所示的4×4小方格中,每格内只填入一个汉字,且任意的两个汉字既不同行也不同列,则不同的填写方法有( )
A.288种 B.144种 C.576种 D.96种
3.从集合{1,2,3,4,5}中任取2个不同的数,作为方程Ax+By=0的系数A,B的值,则形成的不同直线有______条.
4.从2,3,5,7,11中每次选出两个不同的数作为分数的分子、分母,则可产生不同的分数的个数是________,其中真分数的个数是________.
5.用5种颜色给如图所示的四面体ABCD的每条棱着色,要求每条棱只着一种颜色且共顶点的棱着不同的颜色,问有多少种不同的着色方法?
一、选择题
1.将3张不同的奥运会门票分给10名同学中的3人,每人1张,则不同分法的种数是( )
A.2 160 B.720 C.240 D.120
B [第1张门票有10种分法,第2张门票有9种分法,第3张门票有8种分法,由分步乘法计数原理得共有10×9×8=720(种)分法.]
2.用0,1,…,9这10个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252 C.261 D.648
B [0,1,2,…,9共能组成9×10×10=900(个)三位数,其中无重复数字的三位数有9×9×8=648(个),所以有重复数字的三位数有900-648=252(个).]
3.某城市的电话号码由六位升为七位(首位数字均不为零),则该城市可增加的电话部数是( )
A.9×8×7×6×5×4×3×2
B.8×96
C.9×106
D.8.1×106
D [电话号码是六位数字时,该城市可安装电话9×105部,同理升为七位时为9×106,∴可增加的电话数是9×106-9×105=8.1×106.故选D.]
4.有A,B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车床,丙只会操作A种车床,要从这三名工人中选两名分别去操作这两种车床,则不同的选派方法有( )
A.6种 B.5种 C.4种 D.3种
C [不同的选派情况可分为3类:若选甲、乙,有2种方法;若选甲、丙,有1种方法;若选乙、丙,有1种方法.根据分类加法计数原理知,不同的选派方法有2+1+1=4(种).]
5.有四位教师在同一年级的四个班各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则监考的方法有( )
A.8种 B.9种 C.10种 D.11种
B [设四位监考教师分别为A,B,C,D,所教班分别为a,b,c,d.若A监考b,则余下三人监考剩下的三个班,共有3种不同方法.同理,若A监考c,d时,也分别有3种不同方法.由分类加法计数原理,得监考方法共有3+3+3=9(种).]
二、填空题
6.从3名男生和4名女生中选出2人分别担任2项不同的社区活动服务者,要求男、女生各1人,那么不同的安排方法有________种(用数字作答).
24 [先选一名男生,有3种方法;再选一名女生,有4种方法.根据分步乘法计数原理可得选取男、女生各1名,不同的安排方案种数为3×4×2=24.]
7.有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有不同的取法______种.
242 [取两本书中,一本数学、一本语文,根据分步乘法计数原理有10×9=90(种)不同取法;
取两本书中,一本语文、一本英语,有9×8=72(种)不同取法;
取两本书中,一本数学、一本英语,有10×8=80(种)不同取法.
综合以上三类,利用分类加法计数原理,共有90+72+80=242(种)不同取法.]
8.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有________种.
20 [分三类:若甲在周一,则乙丙有4×3=12种排法;若甲在周二,则乙丙有3×2=6种排法;若甲在周三,则乙丙有2×1=2种排法.所以不同的安排方法共有12+6+2=20种.]
三、解答题
9.如图所示,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,不同的涂色方法共有多少种?(用数字作答)
[解] 不妨将图中的4个格子依次编号为①②③④,当①③同色时,有6×5×1×5=150种方法;当①③异色时,有6×5×4×4=480种方法.所以共有150+480=630种方法.
10.用数字1,2,3,4,5,6组成无重复数字的三位数,然后由小到大排成一个数列.
(1)求这个数列的项数;
(2)求这个数列中的第89项的值.
[解] (1)完成这件事需要分别确定百位、十位和个位数,可以先确定百位,再确定十位,最后确定个位,因此要分步相乘.
第一步:确定百位数,有6种方法.
第二步:确定十位数,有5种方法.
第三步:确定个位数,有4种方法.
根据分步乘法计数原理,共有
N=6×5×4=120个三位数.
所以这个数列的项数为120.
(2)这个数列中,百位是1,2,3,4的共有4×5×4=80个,
百位是5的三位数中,十位是1或2的有4+4=8个,
故第88项为526,故从小到大第89项为531.
素养达标
1.一个旅游景区的游览线路如图所示,某人从P点处进,Q点处出,沿图中线路游览A,B,C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )
A.6种 B.8种 C.12种 D.48种
D [每个景区都有2条线路,所以游览第一个景点有6种选法,游览第二个景点有4种选法,游览第三个景点有2种选法,故共有6×4×2=48种不同的游览线路.]
2.将“福”“禄”“寿”填入到如图所示的4×4小方格中,每格内只填入一个汉字,且任意的两个汉字既不同行也不同列,则不同的填写方法有( )
A.288种 B.144种 C.576种 D.96种
C [依题意可分为以下3步:(1)先从16个格子中任选一格放入第一个汉字,有16种方法;(2)任意的两个汉字既不同行也不同列,第二个汉字只有9个格子可以放,有9种方法;(3)第三个汉字只有4个格子可以放,有4种方法.根据分步乘法计数原理,可得不同的填写方法有16×9×4=576(种).]
3.从集合{1,2,3,4,5}中任取2个不同的数,作为方程Ax+By=0的系数A,B的值,则形成的不同直线有______条.
18 [第一步,取A的值,有5种取法;第二步,取B的值,有4种取法,其中当A=1,B=2时与A=2,B=4时是相同的方程;当A=2,B=1时与A=4,B=2时是相同的方程,故共有5×4-2=18条.]
4.从2,3,5,7,11中每次选出两个不同的数作为分数的分子、分母,则可产生不同的分数的个数是________,其中真分数的个数是________.
20 10 [产生分数可分两步:第一步,产生分子有5种方法;第二步,产生分母有4种方法,共有5×4=20个分数.产生真分数,可分四类:第一类,当分子是2时,有4个真分数,同理,当分子分别是3,5,7时,真分数的个数分别是3,2,1,共有4+3+2+1=10个真分数.]
5.用5种颜色给如图所示的四面体ABCD的每条棱着色,要求每条棱只着一种颜色且共顶点的棱着不同的颜色,问有多少种不同的着色方法?
[解] 第一步,对棱CD着色,有5种不同的方法.
第二步,对棱CA着色,有4种不同的方法.
第三步,对棱CB着色,有3种不同的方法.
第四步,分两类,依次对AD,AB,BD着色:
第一类,AD与BC同色,AD有1种着色方法,着AB时,当AB与CD同色时,AB有1种着色方法,BD有3种着色方法,当AB与CD不同色时,AB有2种着色方法,BD有2种着色方法;第二类,AD与BC不同色,AD有2种着色方法,着AB时,当AB与CD同色时,AB有1种着色方法,BD有2种着色方法,当AB与CD不同色时,AB有1种着色方法,BD有1种着色方法.综上,利用分类加法计数原理与分步乘法计数原理可得,不同的着色方法共有5×4×3×[1×(1×3+2×2)+2×(1×2+1×1)]=780(种).
一、选择题
1.将3张不同的奥运会门票分给10名同学中的3人,每人1张,则不同分法的种数是( )
A.2 160 B.720 C.240 D.120
2.用0,1,…,9这10个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252 C.261 D.648
3.某城市的电话号码由六位升为七位(首位数字均不为零),则该城市可增加的电话部数是( )
A.9×8×7×6×5×4×3×2
B.8×96
C.9×106
D.8.1×106
4.有A,B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车床,丙只会操作A种车床,要从这三名工人中选两名分别去操作这两种车床,则不同的选派方法有( )
A.6种 B.5种 C.4种 D.3种
5.有四位教师在同一年级的四个班各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则监考的方法有( )
A.8种 B.9种 C.10种 D.11种
二、填空题
6.从3名男生和4名女生中选出2人分别担任2项不同的社区活动服务者,要求男、女生各1人,那么不同的安排方法有________种(用数字作答).
7.有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有不同的取法______种.
8.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有________种.
三、解答题
9.如图所示,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,不同的涂色方法共有多少种?(用数字作答)
10.用数字1,2,3,4,5,6组成无重复数字的三位数,然后由小到大排成一个数列.
(1)求这个数列的项数;
(2)求这个数列中的第89项的值.
素养达标
1.一个旅游景区的游览线路如图所示,某人从P点处进,Q点处出,沿图中线路游览A,B,C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )
A.6种 B.8种 C.12种 D.48种
2.将“福”“禄”“寿”填入到如图所示的4×4小方格中,每格内只填入一个汉字,且任意的两个汉字既不同行也不同列,则不同的填写方法有( )
A.288种 B.144种 C.576种 D.96种
3.从集合{1,2,3,4,5}中任取2个不同的数,作为方程Ax+By=0的系数A,B的值,则形成的不同直线有______条.
4.从2,3,5,7,11中每次选出两个不同的数作为分数的分子、分母,则可产生不同的分数的个数是________,其中真分数的个数是________.
5.用5种颜色给如图所示的四面体ABCD的每条棱着色,要求每条棱只着一种颜色且共顶点的棱着不同的颜色,问有多少种不同的着色方法?
一、选择题
1.将3张不同的奥运会门票分给10名同学中的3人,每人1张,则不同分法的种数是( )
A.2 160 B.720 C.240 D.120
B [第1张门票有10种分法,第2张门票有9种分法,第3张门票有8种分法,由分步乘法计数原理得共有10×9×8=720(种)分法.]
2.用0,1,…,9这10个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252 C.261 D.648
B [0,1,2,…,9共能组成9×10×10=900(个)三位数,其中无重复数字的三位数有9×9×8=648(个),所以有重复数字的三位数有900-648=252(个).]
3.某城市的电话号码由六位升为七位(首位数字均不为零),则该城市可增加的电话部数是( )
A.9×8×7×6×5×4×3×2
B.8×96
C.9×106
D.8.1×106
D [电话号码是六位数字时,该城市可安装电话9×105部,同理升为七位时为9×106,∴可增加的电话数是9×106-9×105=8.1×106.故选D.]
4.有A,B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车床,丙只会操作A种车床,要从这三名工人中选两名分别去操作这两种车床,则不同的选派方法有( )
A.6种 B.5种 C.4种 D.3种
C [不同的选派情况可分为3类:若选甲、乙,有2种方法;若选甲、丙,有1种方法;若选乙、丙,有1种方法.根据分类加法计数原理知,不同的选派方法有2+1+1=4(种).]
5.有四位教师在同一年级的四个班各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则监考的方法有( )
A.8种 B.9种 C.10种 D.11种
B [设四位监考教师分别为A,B,C,D,所教班分别为a,b,c,d.若A监考b,则余下三人监考剩下的三个班,共有3种不同方法.同理,若A监考c,d时,也分别有3种不同方法.由分类加法计数原理,得监考方法共有3+3+3=9(种).]
二、填空题
6.从3名男生和4名女生中选出2人分别担任2项不同的社区活动服务者,要求男、女生各1人,那么不同的安排方法有________种(用数字作答).
24 [先选一名男生,有3种方法;再选一名女生,有4种方法.根据分步乘法计数原理可得选取男、女生各1名,不同的安排方案种数为3×4×2=24.]
7.有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有不同的取法______种.
242 [取两本书中,一本数学、一本语文,根据分步乘法计数原理有10×9=90(种)不同取法;
取两本书中,一本语文、一本英语,有9×8=72(种)不同取法;
取两本书中,一本数学、一本英语,有10×8=80(种)不同取法.
综合以上三类,利用分类加法计数原理,共有90+72+80=242(种)不同取法.]
8.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有________种.
20 [分三类:若甲在周一,则乙丙有4×3=12种排法;若甲在周二,则乙丙有3×2=6种排法;若甲在周三,则乙丙有2×1=2种排法.所以不同的安排方法共有12+6+2=20种.]
三、解答题
9.如图所示,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,不同的涂色方法共有多少种?(用数字作答)
[解] 不妨将图中的4个格子依次编号为①②③④,当①③同色时,有6×5×1×5=150种方法;当①③异色时,有6×5×4×4=480种方法.所以共有150+480=630种方法.
10.用数字1,2,3,4,5,6组成无重复数字的三位数,然后由小到大排成一个数列.
(1)求这个数列的项数;
(2)求这个数列中的第89项的值.
[解] (1)完成这件事需要分别确定百位、十位和个位数,可以先确定百位,再确定十位,最后确定个位,因此要分步相乘.
第一步:确定百位数,有6种方法.
第二步:确定十位数,有5种方法.
第三步:确定个位数,有4种方法.
根据分步乘法计数原理,共有
N=6×5×4=120个三位数.
所以这个数列的项数为120.
(2)这个数列中,百位是1,2,3,4的共有4×5×4=80个,
百位是5的三位数中,十位是1或2的有4+4=8个,
故第88项为526,故从小到大第89项为531.
素养达标
1.一个旅游景区的游览线路如图所示,某人从P点处进,Q点处出,沿图中线路游览A,B,C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )
A.6种 B.8种 C.12种 D.48种
D [每个景区都有2条线路,所以游览第一个景点有6种选法,游览第二个景点有4种选法,游览第三个景点有2种选法,故共有6×4×2=48种不同的游览线路.]
2.将“福”“禄”“寿”填入到如图所示的4×4小方格中,每格内只填入一个汉字,且任意的两个汉字既不同行也不同列,则不同的填写方法有( )
A.288种 B.144种 C.576种 D.96种
C [依题意可分为以下3步:(1)先从16个格子中任选一格放入第一个汉字,有16种方法;(2)任意的两个汉字既不同行也不同列,第二个汉字只有9个格子可以放,有9种方法;(3)第三个汉字只有4个格子可以放,有4种方法.根据分步乘法计数原理,可得不同的填写方法有16×9×4=576(种).]
3.从集合{1,2,3,4,5}中任取2个不同的数,作为方程Ax+By=0的系数A,B的值,则形成的不同直线有______条.
18 [第一步,取A的值,有5种取法;第二步,取B的值,有4种取法,其中当A=1,B=2时与A=2,B=4时是相同的方程;当A=2,B=1时与A=4,B=2时是相同的方程,故共有5×4-2=18条.]
4.从2,3,5,7,11中每次选出两个不同的数作为分数的分子、分母,则可产生不同的分数的个数是________,其中真分数的个数是________.
20 10 [产生分数可分两步:第一步,产生分子有5种方法;第二步,产生分母有4种方法,共有5×4=20个分数.产生真分数,可分四类:第一类,当分子是2时,有4个真分数,同理,当分子分别是3,5,7时,真分数的个数分别是3,2,1,共有4+3+2+1=10个真分数.]
5.用5种颜色给如图所示的四面体ABCD的每条棱着色,要求每条棱只着一种颜色且共顶点的棱着不同的颜色,问有多少种不同的着色方法?
[解] 第一步,对棱CD着色,有5种不同的方法.
第二步,对棱CA着色,有4种不同的方法.
第三步,对棱CB着色,有3种不同的方法.
第四步,分两类,依次对AD,AB,BD着色:
第一类,AD与BC同色,AD有1种着色方法,着AB时,当AB与CD同色时,AB有1种着色方法,BD有3种着色方法,当AB与CD不同色时,AB有2种着色方法,BD有2种着色方法;第二类,AD与BC不同色,AD有2种着色方法,着AB时,当AB与CD同色时,AB有1种着色方法,BD有2种着色方法,当AB与CD不同色时,AB有1种着色方法,BD有1种着色方法.综上,利用分类加法计数原理与分步乘法计数原理可得,不同的着色方法共有5×4×3×[1×(1×3+2×2)+2×(1×2+1×1)]=780(种).
