【备考2022】近十年(2012-2021)全国各地高考数学真题分类汇编 函数小题(含解析)
文档属性
| 名称 | 【备考2022】近十年(2012-2021)全国各地高考数学真题分类汇编 函数小题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 10:39:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2012-2021十年全国卷高考数学真题分类精编
函数小题
(精解精析)
一、选择题
1.(2021年全国甲卷(文))下列函数中是增函数的为(
)
A.
B.
C.
D.
2.(2021年全国甲卷(文))设是定义域为R的奇函数,且;若,则(
)
A.
B.
C.
D.
3.(2021年高考全国乙卷理科)设函数,则下列函数中为奇函数的是
( )
A.
B.
C.
D.
4.(2021年高考全国甲卷理科)设函数的定义域为R,为奇函数,为偶函数,
当时,.若,则
( )
A.
B.
C.
D.
5.(2021年高考全国甲卷理科)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录表的数据V的满足.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为( )()
A.1.5
B.1.2
C.0.8
D.0.6
6.(2021年浙江卷)已知函数,则图象为如图的函数可能是(
)
A.
B.
C.
D.
7.(2020年高考数学课标Ⅰ卷理科)若,则( )
A.
B.
C.
D.
8.(2020年高考数学课标Ⅰ卷理科)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据得到下面的散点图:
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A
B.
C.
D.
9.(2020年高考数学课标Ⅱ卷理科)若,则
( )
A.
B.
C.
D.
10.(2020年高考数学课标Ⅱ卷理科)设函数,则( )
A.是偶函数,且在单调递增
B.是奇函数,且在单调递减
C.是偶函数,且在单调递增
D.是奇函数,且在单调递减
11.(2020年高考数学课标Ⅱ卷理科)在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05,志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者
( )
A.10名
B.18名
C.24名
D.32名
12.(2020年高考数学课标Ⅲ卷理科)已知,,设,,,则(
)
( )
A
B.
C.
D.
13.(2020年高考数学课标Ⅲ卷理科)Logistic模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:
,其中K为最大确诊病例数.当时,标志着已初步遏制疫情,则
约为
( )(ln19≈3)
A.60
B.63
C.66
D.69
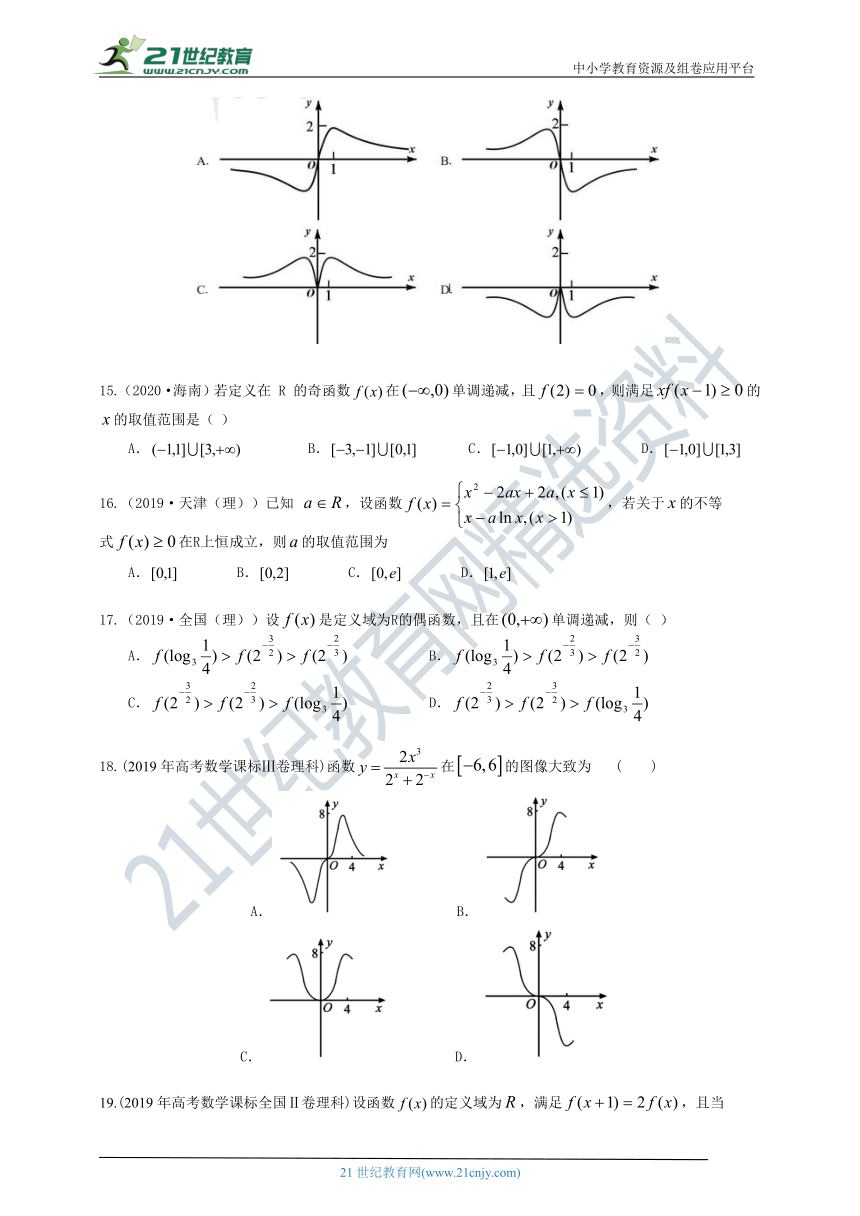
14.(2020·天津)函数的图象大致为(
)
15.(2020·海南)若定义在
R
的奇函数在单调递减,且,则满足的的取值范围是(
)
A.
B.
C.
D.
16.(2019·天津(理))已知
,设函数,若关于的不等
式在R上恒成立,则的取值范围为
A.
B.
C.
D.
17.(2019·全国(理))设是定义域为R的偶函数,且在单调递减,则(
)
A.
B.
C.
D.
18.(2019年高考数学课标Ⅲ卷理科)函数在的图像大致为
( )
A.
B.
C.
D.
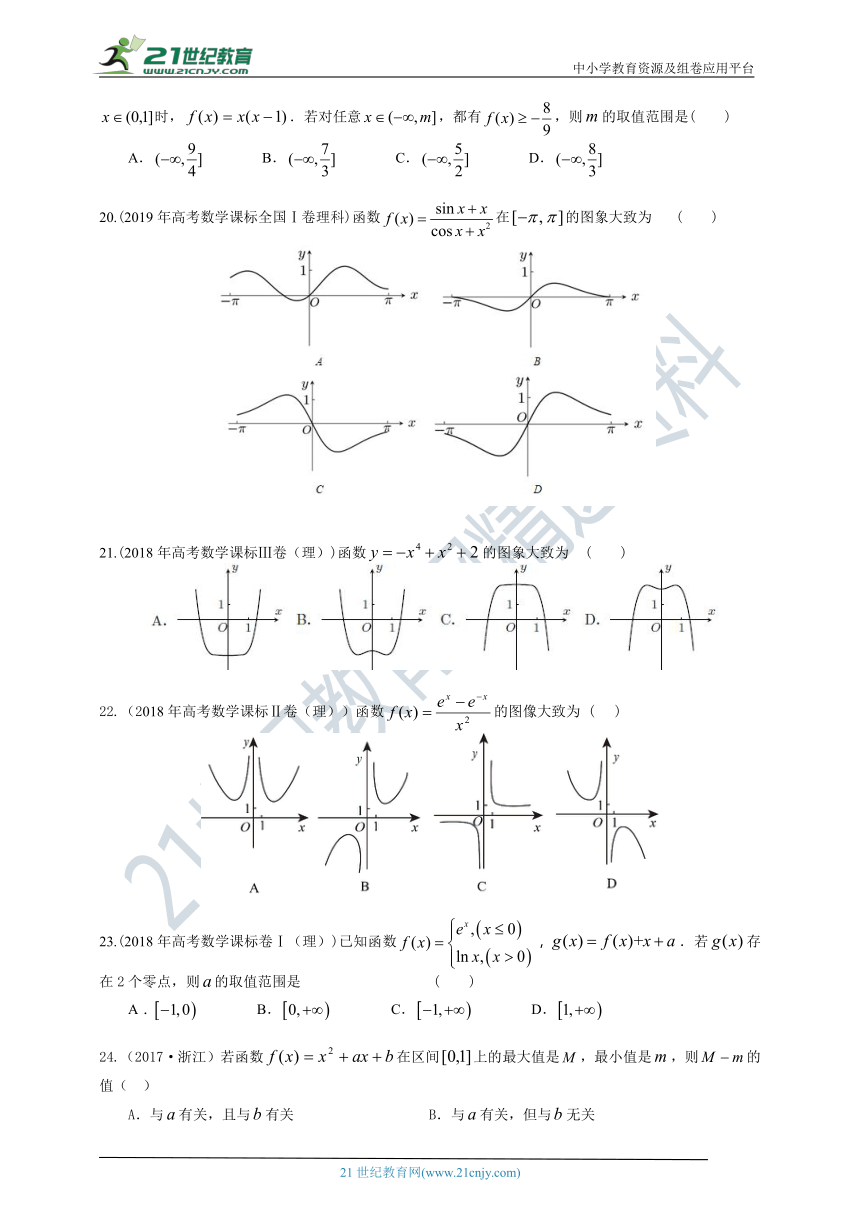
19.(2019年高考数学课标全国Ⅱ卷理科)设函数的定义域为,满足,且当
时,.若对任意,都有,则的取值范围是( )
A.
B.
C.
D.
20.(2019年高考数学课标全国Ⅰ卷理科)函数在的图象大致为
( )
21.(2018年高考数学课标Ⅲ卷(理))函数的图象大致为
( )
22.(2018年高考数学课标Ⅱ卷(理))函数的图像大致为
(
)
23.(2018年高考数学课标卷Ⅰ(理))已知函数,.若存在2个零点,则的取值范围是
( )
A.
B.
C.
D.
24.(2017·浙江)若函数在区间上的最大值是,最小值是,则的值(
)
A.与有关,且与有关
B.与有关,但与无关
C.与无关,且与无关
D.与无关,但与有关
25.(2017·天津(理))已知奇函数在上是增函数,,若,,
,则
的大小关系为(
)
A.
B.
C.
D.
26.(2017年高考数学新课标Ⅰ卷理科)设为正数,且,则
( )
A.
B.
C.
D.
27.(2017年高考数学新课标Ⅰ卷理科)函数在单调递减,且为奇函数.若,则满足的的取值范围是
( )
A.
B.
C.
D.
28.(2017年高考数学课标Ⅲ卷理科)已知函数有唯一零点,则( )
A.
B.
C.
D.
29.(2017年高考数学课标Ⅲ卷理科)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是
( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
30.(2016高考数学课标Ⅲ卷理科)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为C.B点表示四月的平均最低气温约为C.下面叙述不正确的是
( )
A.各月的平均最低气温都在C以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于C的月份有5个
31.(2016高考数学课标Ⅰ卷理科)函数在的图像大致为
( )
32.(2016·天津(文))已知是定义在
R
上的偶函数,且在区间上单调递增,若实
数满足,则的取值范围是(
)
A.
B.
C.
D.
33.(2015高考数学新课标2理科)设函数,
( )
A.3
B.6
C.9
D.12
34.(2015·全国(文))设函数,则使成立的的取值
范围是()
A.
B.
C.
D.
35.(2014·全国(理))设函数的定义域为,且是奇函数,是偶函数,则下列结论中正确的是(
)
A.是偶函数
B.是奇函数
C.是奇函数
D.是奇函数
36.(2013高考数学新课标2理科)设,,,则
( )
A.
B.
C.
D.
37.(2013·天津(文))已知函数是定义在R上的偶函数,且在区间单调递增,若实数满
足,则的取值范围是()
A.
B.
C.
D.
38.(2012高考数学新课标理科)已知函数,则的图象大致为
( )
39.(2012·山东(文))函数的定义域为(
)
A.
B.
C.
D.
40.(2012·福建(理))函数在上有定义,若对任意,有
,则称在上具有性质
P;设在上具有性质
P,
现给出如下命题:
①在上的图像是连续不断的;
②在上具有性质
P;
③若在处取得最大值
1,则,;
④对,有,其中真命题的序号是(
)
A.①②
B.①③
C.②④
D.③④
二、填空题
41.(2021年新高考1卷)已知函数是偶函数,则______.
42.(2021年浙江卷)已知,函数若,则______.
43.(2019年高考数学课标全国Ⅱ卷理科)已知是奇函数,且当时,.若
,则
.
44.(2017年高考数学课标Ⅲ卷理科)设函数,则满足的的取值范围是
.
45.(2017·全国(理))设函数,
则满足的的取值范围是
.
46.(2017·江苏)已知函数,其中是自然数对数的底数,若
,则实数的取值范围是
.
47.(2016·北京(理))设函数
①若,则的最大值为
;
②若无最大值,则实数的取值范围是
.
48.(2016·江苏)设
是定义在
R
上且周期为
2
的函数,在区间上,
,若,则的值是
.
49.(2015高考数学新课标1理科)若函数为偶函数,则
.
50.(2015·浙江(文))已知函数,则
;的最小值是
.
51.(2015·
福建(理))若函数的值域为,则实数的取值范围是
.
52.(2014高考数学课标2理科)已知偶函数在单调递减,.若,则的取值范围是__________.
53.(2013高考数学新课标1理科)若函数的图像关于直线对称,则的最大值是______.
三.参考答案
1.【答案】D
解析:对于A,为上的减函数,不合题意,舍.
对于B,为上的减函数,不合题意,舍.
对于C,在为减函数,不合题意,舍.
对于D,为上的增函数,符合题意,故选:D.
2.【答案】C
解析:由题意可得:,
而,
故.
故选:C.
3.【答案】B
解析:由题意可得,
对于A,不是奇函数;
对于B,是奇函数;
对于C,,定义域不关于原点对称,不是奇函数;
对于D,,定义域不关于原点对称,不是奇函数.故选:B
4.【答案】D
解析:因为是奇函数,所以①;
因为是偶函数,所以②.
令,由①得:,由②得:
因为,所以所以,
令,由①得:,所以
思路一:从定义入手.
所以.
思路二:从周期性入手
由两个对称性可知,函数的周期.
所以.故选:D.
5.【答案】C
解析:由,当时,,
则.
故选:C.
6.【答案】D
【详解】对于A,,该函数非奇非偶函数,与函数图象不符,排除A;
对于B,,该函数为非奇非偶函数,与函数图象不符,排除B;
对于C,,则,
当时,,与图象不符,排除C;故选:D.
7.【答案】B
解析:设,则为增函数,
∵,
∴
所以,所以.
当时,,此时,有
当时,,此时,有,所以C、D错误.
故选:B.
8.【答案】D
解析:由散点图分布可知,散点图分布在一个对数函数的图象附近,
因此,最适合作为发芽率和温度的回归方程类型的是.
故选:D.
9.【答案】A
解析:由
得:,
令
为上的增函数,为上的减函数,所以为上的增函数,
,,,则A正确,B错误;
与的大小不确定,故CD无法确定.故选:A.
10.【答案】D
解析:由得定义域为,关于坐标原点对称,
又,
所以为定义域上的奇函数,可排除AC;
当时,,在上单调递增,在上单调递减,所以在上单调递增,排除B;
当时,,
在上单调递减,在定义域内单调递增,
根据复合函数单调性可知:在上单调递减,D正确.故选:D.
11.【答案】B
解析:由题意,第二天新增订单数为,设需要志愿者x名,
,,故需要志愿者名.故选:B
12.【答案】A
解析:由题意可知,
,;
由,得,由,得,,可得;
由,得,由,得,,可得.
综上所述,.
故选:A.
13.【答案】C
解析:,所以,则,
所以,解得.
故选:C.
14.【答案】A
解析:由函数的解析式可得:,则函数为奇函数,其图象关于
坐标原点对称,选项CD错误;
当时,,选项B错误;
故选:A.
15.【答案】D
解析:因为定义在上的奇函数在单调递减,且,
所以在上也是单调递减,且,,
所以当时,,当时,,
所以由可得:
或或.
解得或,
所以满足的的取值范围是,故选:D.
16.【答案】C
解析:(1)当时,二次函数的对称轴为,需.∴.
而,,在单调递增。
此时要使在上恒成立,需.显然成立.
可知.
(2)当时,,,显然成立.
而,
当时,,单调递减;当时,,单调递增。
要使,需,可知;
综上,,故选C.
17.【答案】C
解析:因为是R上的偶函数,所以.
而,
又在单调递减,
,故选C.
18.【答案】B
解析:设,则,所以是奇函数,图象关于原点成中心对称,排除选项C.又,排除选项A、D,故选B.
19.【答案】B
解析:∵时,,,∴,即右移个单位,图像变为原来的2倍.
如图所示:当时,,令,整理得:,∴(舍),∴,
∴时,成立,即,∴,故选B
.
20.【答案】D
解析:显然为奇函数,故排除A,当在轴右侧开始取值时,,排除C,
又,故选D.
21.【答案】D
解析:易知函数为偶函数,而,所以当时,;当时,,所以函数在、上单调递增,在、上单调递减,故选D.
22.【答案】B
解析:因为,,所以为奇函数,排除A;,排除D;
因为,当时,,函数单
调递增,排除C.故选B.
23.【答案】C
解析:由得,作出函数和的图象如图
当直线的截距,即时,两个函数的图象都有2个交点,即函数存在2个零点,故实数的取值范围是,故选C.
24【答案】B
解析:因为最值在,,中取,所以最值之差一定与
有关,与无关,故选B.
25.【答案】C
解析:∵是上的奇函数,∴是上的偶函数.
∴.
∵奇函数在上是增函数,
∴当时,,.
∴当时,恒成立,
∴在上是增函数.
∵,,∴
结合函数的性质得;故选C.
26.【答案】D
解析:令,则,,
∴,则
,则,故选D.
27.【答案】
D
解析:因为为奇函数且在上单调递减,要使成立,则满足,所以由得,即使成立的满足,选D.
28.【答案】C
解析:法一:,
设,
当时,,当时,,函数单调递减;当时,,函数单调递增,当时,函数取得最小值,设,当时,函数取得最小值,若,函数和没有交点,当时,时,函数
和有一个交点,即,所以,故选C.
法二:由条件,,得:
所以,即为的对称轴
由题意,有唯一零点,∴的零点只能为即
解得.
29.【答案】
A
解析:观察折线图,每年7月到8月折线图呈下降趋势,月接待游客量减少,故选项A说法错误;
折线图整体呈现出增长的趋势,年接待游客量逐年增加,故选项B说法正确;
每年的接待游客量七、八月份达到最高点,即各年的月接待游客量高峰期大致在7,8月,故选项C说法正确;
每年1月至6月的折线图比较平稳,月接待游客量波动性较小,而每年7月至12月的折线图不平稳,波动性较大,故选项D说法正确.
故选A.
30.【答案】D
解析:由图可知C均在阴影框内,所以各月的平均最低气温都在C以上,A正确;由图可知在七月的平均温差大于C,而一月的平均温差小于C,所以七月的平均温差比一月的平均温差大,B正确;由图可知三月和十一月的平均最高气温都大约在C,基本相同,C正确;由图可知平均最高气温高于C的月份有3个或2个,所以D不正确.故选D.
31.【答案】D
解析:函数在上是偶函数,其图象关于轴对称,因为
,所以排除选项;当时,有一零点,设为,当时,为减函数,当时,为增函数.故选D.
32.【答案】C
解析:是定义在R上的偶函数,
在区间单调递增,所以在区间单调递减,
所以,解得
33.【答案】C
解析:由已知得,又,所以
,故,故选C.
34.【答案】A
解析:函数的定义域为R,又由题意可知,故为偶函数.
当时,,因为单调递增,亦为单调递增,
所以在为增函数.
由,所以故而,解得.故选A
35.【答案】C
解析:设,则,∵是奇函数,是偶函数,∴,为奇函数,选C.
36.【答案】D
解析:,,,显然
37.【答案】C
解析:是定义在R上的偶函数,
而,所以
在区间单调递增,所以,解得
38.【答案】B
解析:设,则
∴在上为增函数,在上为减函数
∴
∴
得:或均有
排除A,C,D
故选
B
39.【答案】B
解析:由,解得
40.【答案】D
解析:正确理解和推断可知①②错误,③④正确.
41.解析:因为,故,
因为为偶函数,故,
,整理得到,故,
故答案为:1
42.解析:,故,
故答案为:2.
43.解析:因为是奇函数,且当时,.又因为,,
所以,两边取以为底的对数得,所以,即.
44.解析:法一:因为
当时,;
当时,;
当时,由,可解得
综上可知满足的的取值范围是.
法二:,,即
由图象变换可画出与的图象如下:
由图可知,满足的解为.
法三:当且时,由得,得,又因为是上的增函数,所以当增大时,增大,所以满足的的取值范围是.
45.解析:由题意得:
当时,
恒成立,即;当时,
恒成立,即;当时,即,
即;综上,的取值范围是.
46.解析:因为
,所以函数是奇函数,
因为,所以函数在R
上单调递增,又,即
,所以,解得,故实数的取值范围为
47.解析:如图,作出函数与直线的图象,它们的交点是A(?1,
2),
O(0,
0),
B(1,
?2)
,由,知
是函数的极小值点,①当
时,
,由图象可知的最大值是;
②由图象知当时,有最大值
;只有当时,,无最大值,所以所求
的取值范围是.
48.解析:,所以
49.解析:由题知是奇函数,所以
即,解得.
50.解析:如图根据所给函数的解析式结合其单调性作出其图像如图所示,易知,
51.解析:函数的值域为,故当
时,满足,当时,
由,所以,所以,所以实数的取值范围
52.解析:因为是偶函数,所以不等式,因为在上单调递减,所以,解得
53.解析:由图像关于直线对称,则
,
,解得,
∴
∴
当时,,
当时,,
∴在单调递增,在单调递减,在单调递
增,在单调递减,故当和时取极大值,
C
B
A
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2012-2021十年全国卷高考数学真题分类精编
函数小题
(精解精析)
一、选择题
1.(2021年全国甲卷(文))下列函数中是增函数的为(
)
A.
B.
C.
D.
2.(2021年全国甲卷(文))设是定义域为R的奇函数,且;若,则(
)
A.
B.
C.
D.
3.(2021年高考全国乙卷理科)设函数,则下列函数中为奇函数的是
( )
A.
B.
C.
D.
4.(2021年高考全国甲卷理科)设函数的定义域为R,为奇函数,为偶函数,
当时,.若,则
( )
A.
B.
C.
D.
5.(2021年高考全国甲卷理科)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录表的数据V的满足.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为( )()
A.1.5
B.1.2
C.0.8
D.0.6
6.(2021年浙江卷)已知函数,则图象为如图的函数可能是(
)
A.
B.
C.
D.
7.(2020年高考数学课标Ⅰ卷理科)若,则( )
A.
B.
C.
D.
8.(2020年高考数学课标Ⅰ卷理科)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据得到下面的散点图:
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A
B.
C.
D.
9.(2020年高考数学课标Ⅱ卷理科)若,则
( )
A.
B.
C.
D.
10.(2020年高考数学课标Ⅱ卷理科)设函数,则( )
A.是偶函数,且在单调递增
B.是奇函数,且在单调递减
C.是偶函数,且在单调递增
D.是奇函数,且在单调递减
11.(2020年高考数学课标Ⅱ卷理科)在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05,志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者
( )
A.10名
B.18名
C.24名
D.32名
12.(2020年高考数学课标Ⅲ卷理科)已知,,设,,,则(
)
( )
A
B.
C.
D.
13.(2020年高考数学课标Ⅲ卷理科)Logistic模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:
,其中K为最大确诊病例数.当时,标志着已初步遏制疫情,则
约为
( )(ln19≈3)
A.60
B.63
C.66
D.69
14.(2020·天津)函数的图象大致为(
)
15.(2020·海南)若定义在
R
的奇函数在单调递减,且,则满足的的取值范围是(
)
A.
B.
C.
D.
16.(2019·天津(理))已知
,设函数,若关于的不等
式在R上恒成立,则的取值范围为
A.
B.
C.
D.
17.(2019·全国(理))设是定义域为R的偶函数,且在单调递减,则(
)
A.
B.
C.
D.
18.(2019年高考数学课标Ⅲ卷理科)函数在的图像大致为
( )
A.
B.
C.
D.
19.(2019年高考数学课标全国Ⅱ卷理科)设函数的定义域为,满足,且当
时,.若对任意,都有,则的取值范围是( )
A.
B.
C.
D.
20.(2019年高考数学课标全国Ⅰ卷理科)函数在的图象大致为
( )
21.(2018年高考数学课标Ⅲ卷(理))函数的图象大致为
( )
22.(2018年高考数学课标Ⅱ卷(理))函数的图像大致为
(
)
23.(2018年高考数学课标卷Ⅰ(理))已知函数,.若存在2个零点,则的取值范围是
( )
A.
B.
C.
D.
24.(2017·浙江)若函数在区间上的最大值是,最小值是,则的值(
)
A.与有关,且与有关
B.与有关,但与无关
C.与无关,且与无关
D.与无关,但与有关
25.(2017·天津(理))已知奇函数在上是增函数,,若,,
,则
的大小关系为(
)
A.
B.
C.
D.
26.(2017年高考数学新课标Ⅰ卷理科)设为正数,且,则
( )
A.
B.
C.
D.
27.(2017年高考数学新课标Ⅰ卷理科)函数在单调递减,且为奇函数.若,则满足的的取值范围是
( )
A.
B.
C.
D.
28.(2017年高考数学课标Ⅲ卷理科)已知函数有唯一零点,则( )
A.
B.
C.
D.
29.(2017年高考数学课标Ⅲ卷理科)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是
( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
30.(2016高考数学课标Ⅲ卷理科)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为C.B点表示四月的平均最低气温约为C.下面叙述不正确的是
( )
A.各月的平均最低气温都在C以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于C的月份有5个
31.(2016高考数学课标Ⅰ卷理科)函数在的图像大致为
( )
32.(2016·天津(文))已知是定义在
R
上的偶函数,且在区间上单调递增,若实
数满足,则的取值范围是(
)
A.
B.
C.
D.
33.(2015高考数学新课标2理科)设函数,
( )
A.3
B.6
C.9
D.12
34.(2015·全国(文))设函数,则使成立的的取值
范围是()
A.
B.
C.
D.
35.(2014·全国(理))设函数的定义域为,且是奇函数,是偶函数,则下列结论中正确的是(
)
A.是偶函数
B.是奇函数
C.是奇函数
D.是奇函数
36.(2013高考数学新课标2理科)设,,,则
( )
A.
B.
C.
D.
37.(2013·天津(文))已知函数是定义在R上的偶函数,且在区间单调递增,若实数满
足,则的取值范围是()
A.
B.
C.
D.
38.(2012高考数学新课标理科)已知函数,则的图象大致为
( )
39.(2012·山东(文))函数的定义域为(
)
A.
B.
C.
D.
40.(2012·福建(理))函数在上有定义,若对任意,有
,则称在上具有性质
P;设在上具有性质
P,
现给出如下命题:
①在上的图像是连续不断的;
②在上具有性质
P;
③若在处取得最大值
1,则,;
④对,有,其中真命题的序号是(
)
A.①②
B.①③
C.②④
D.③④
二、填空题
41.(2021年新高考1卷)已知函数是偶函数,则______.
42.(2021年浙江卷)已知,函数若,则______.
43.(2019年高考数学课标全国Ⅱ卷理科)已知是奇函数,且当时,.若
,则
.
44.(2017年高考数学课标Ⅲ卷理科)设函数,则满足的的取值范围是
.
45.(2017·全国(理))设函数,
则满足的的取值范围是
.
46.(2017·江苏)已知函数,其中是自然数对数的底数,若
,则实数的取值范围是
.
47.(2016·北京(理))设函数
①若,则的最大值为
;
②若无最大值,则实数的取值范围是
.
48.(2016·江苏)设
是定义在
R
上且周期为
2
的函数,在区间上,
,若,则的值是
.
49.(2015高考数学新课标1理科)若函数为偶函数,则
.
50.(2015·浙江(文))已知函数,则
;的最小值是
.
51.(2015·
福建(理))若函数的值域为,则实数的取值范围是
.
52.(2014高考数学课标2理科)已知偶函数在单调递减,.若,则的取值范围是__________.
53.(2013高考数学新课标1理科)若函数的图像关于直线对称,则的最大值是______.
三.参考答案
1.【答案】D
解析:对于A,为上的减函数,不合题意,舍.
对于B,为上的减函数,不合题意,舍.
对于C,在为减函数,不合题意,舍.
对于D,为上的增函数,符合题意,故选:D.
2.【答案】C
解析:由题意可得:,
而,
故.
故选:C.
3.【答案】B
解析:由题意可得,
对于A,不是奇函数;
对于B,是奇函数;
对于C,,定义域不关于原点对称,不是奇函数;
对于D,,定义域不关于原点对称,不是奇函数.故选:B
4.【答案】D
解析:因为是奇函数,所以①;
因为是偶函数,所以②.
令,由①得:,由②得:
因为,所以所以,
令,由①得:,所以
思路一:从定义入手.
所以.
思路二:从周期性入手
由两个对称性可知,函数的周期.
所以.故选:D.
5.【答案】C
解析:由,当时,,
则.
故选:C.
6.【答案】D
【详解】对于A,,该函数非奇非偶函数,与函数图象不符,排除A;
对于B,,该函数为非奇非偶函数,与函数图象不符,排除B;
对于C,,则,
当时,,与图象不符,排除C;故选:D.
7.【答案】B
解析:设,则为增函数,
∵,
∴
所以,所以.
当时,,此时,有
当时,,此时,有,所以C、D错误.
故选:B.
8.【答案】D
解析:由散点图分布可知,散点图分布在一个对数函数的图象附近,
因此,最适合作为发芽率和温度的回归方程类型的是.
故选:D.
9.【答案】A
解析:由
得:,
令
为上的增函数,为上的减函数,所以为上的增函数,
,,,则A正确,B错误;
与的大小不确定,故CD无法确定.故选:A.
10.【答案】D
解析:由得定义域为,关于坐标原点对称,
又,
所以为定义域上的奇函数,可排除AC;
当时,,在上单调递增,在上单调递减,所以在上单调递增,排除B;
当时,,
在上单调递减,在定义域内单调递增,
根据复合函数单调性可知:在上单调递减,D正确.故选:D.
11.【答案】B
解析:由题意,第二天新增订单数为,设需要志愿者x名,
,,故需要志愿者名.故选:B
12.【答案】A
解析:由题意可知,
,;
由,得,由,得,,可得;
由,得,由,得,,可得.
综上所述,.
故选:A.
13.【答案】C
解析:,所以,则,
所以,解得.
故选:C.
14.【答案】A
解析:由函数的解析式可得:,则函数为奇函数,其图象关于
坐标原点对称,选项CD错误;
当时,,选项B错误;
故选:A.
15.【答案】D
解析:因为定义在上的奇函数在单调递减,且,
所以在上也是单调递减,且,,
所以当时,,当时,,
所以由可得:
或或.
解得或,
所以满足的的取值范围是,故选:D.
16.【答案】C
解析:(1)当时,二次函数的对称轴为,需.∴.
而,,在单调递增。
此时要使在上恒成立,需.显然成立.
可知.
(2)当时,,,显然成立.
而,
当时,,单调递减;当时,,单调递增。
要使,需,可知;
综上,,故选C.
17.【答案】C
解析:因为是R上的偶函数,所以.
而,
又在单调递减,
,故选C.
18.【答案】B
解析:设,则,所以是奇函数,图象关于原点成中心对称,排除选项C.又,排除选项A、D,故选B.
19.【答案】B
解析:∵时,,,∴,即右移个单位,图像变为原来的2倍.
如图所示:当时,,令,整理得:,∴(舍),∴,
∴时,成立,即,∴,故选B
.
20.【答案】D
解析:显然为奇函数,故排除A,当在轴右侧开始取值时,,排除C,
又,故选D.
21.【答案】D
解析:易知函数为偶函数,而,所以当时,;当时,,所以函数在、上单调递增,在、上单调递减,故选D.
22.【答案】B
解析:因为,,所以为奇函数,排除A;,排除D;
因为,当时,,函数单
调递增,排除C.故选B.
23.【答案】C
解析:由得,作出函数和的图象如图
当直线的截距,即时,两个函数的图象都有2个交点,即函数存在2个零点,故实数的取值范围是,故选C.
24【答案】B
解析:因为最值在,,中取,所以最值之差一定与
有关,与无关,故选B.
25.【答案】C
解析:∵是上的奇函数,∴是上的偶函数.
∴.
∵奇函数在上是增函数,
∴当时,,.
∴当时,恒成立,
∴在上是增函数.
∵,,∴
结合函数的性质得;故选C.
26.【答案】D
解析:令,则,,
∴,则
,则,故选D.
27.【答案】
D
解析:因为为奇函数且在上单调递减,要使成立,则满足,所以由得,即使成立的满足,选D.
28.【答案】C
解析:法一:,
设,
当时,,当时,,函数单调递减;当时,,函数单调递增,当时,函数取得最小值,设,当时,函数取得最小值,若,函数和没有交点,当时,时,函数
和有一个交点,即,所以,故选C.
法二:由条件,,得:
所以,即为的对称轴
由题意,有唯一零点,∴的零点只能为即
解得.
29.【答案】
A
解析:观察折线图,每年7月到8月折线图呈下降趋势,月接待游客量减少,故选项A说法错误;
折线图整体呈现出增长的趋势,年接待游客量逐年增加,故选项B说法正确;
每年的接待游客量七、八月份达到最高点,即各年的月接待游客量高峰期大致在7,8月,故选项C说法正确;
每年1月至6月的折线图比较平稳,月接待游客量波动性较小,而每年7月至12月的折线图不平稳,波动性较大,故选项D说法正确.
故选A.
30.【答案】D
解析:由图可知C均在阴影框内,所以各月的平均最低气温都在C以上,A正确;由图可知在七月的平均温差大于C,而一月的平均温差小于C,所以七月的平均温差比一月的平均温差大,B正确;由图可知三月和十一月的平均最高气温都大约在C,基本相同,C正确;由图可知平均最高气温高于C的月份有3个或2个,所以D不正确.故选D.
31.【答案】D
解析:函数在上是偶函数,其图象关于轴对称,因为
,所以排除选项;当时,有一零点,设为,当时,为减函数,当时,为增函数.故选D.
32.【答案】C
解析:是定义在R上的偶函数,
在区间单调递增,所以在区间单调递减,
所以,解得
33.【答案】C
解析:由已知得,又,所以
,故,故选C.
34.【答案】A
解析:函数的定义域为R,又由题意可知,故为偶函数.
当时,,因为单调递增,亦为单调递增,
所以在为增函数.
由,所以故而,解得.故选A
35.【答案】C
解析:设,则,∵是奇函数,是偶函数,∴,为奇函数,选C.
36.【答案】D
解析:,,,显然
37.【答案】C
解析:是定义在R上的偶函数,
而,所以
在区间单调递增,所以,解得
38.【答案】B
解析:设,则
∴在上为增函数,在上为减函数
∴
∴
得:或均有
排除A,C,D
故选
B
39.【答案】B
解析:由,解得
40.【答案】D
解析:正确理解和推断可知①②错误,③④正确.
41.解析:因为,故,
因为为偶函数,故,
,整理得到,故,
故答案为:1
42.解析:,故,
故答案为:2.
43.解析:因为是奇函数,且当时,.又因为,,
所以,两边取以为底的对数得,所以,即.
44.解析:法一:因为
当时,;
当时,;
当时,由,可解得
综上可知满足的的取值范围是.
法二:,,即
由图象变换可画出与的图象如下:
由图可知,满足的解为.
法三:当且时,由得,得,又因为是上的增函数,所以当增大时,增大,所以满足的的取值范围是.
45.解析:由题意得:
当时,
恒成立,即;当时,
恒成立,即;当时,即,
即;综上,的取值范围是.
46.解析:因为
,所以函数是奇函数,
因为,所以函数在R
上单调递增,又,即
,所以,解得,故实数的取值范围为
47.解析:如图,作出函数与直线的图象,它们的交点是A(?1,
2),
O(0,
0),
B(1,
?2)
,由,知
是函数的极小值点,①当
时,
,由图象可知的最大值是;
②由图象知当时,有最大值
;只有当时,,无最大值,所以所求
的取值范围是.
48.解析:,所以
49.解析:由题知是奇函数,所以
即,解得.
50.解析:如图根据所给函数的解析式结合其单调性作出其图像如图所示,易知,
51.解析:函数的值域为,故当
时,满足,当时,
由,所以,所以,所以实数的取值范围
52.解析:因为是偶函数,所以不等式,因为在上单调递减,所以,解得
53.解析:由图像关于直线对称,则
,
,解得,
∴
∴
当时,,
当时,,
∴在单调递增,在单调递减,在单调递
增,在单调递减,故当和时取极大值,
C
B
A
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
